Книга: Укрощение бесконечности. История математики от первых чисел до теории хаоса
Назад: Индийские цифры
Дальше: Индийская система
Брахмагупта, Махавира и Бхаскара
Самыми выдающимися математиками Древней Индии считают Арьябхату (род. 476), Брахмагупту (род. 598), Махавиру (XI в.) и Бхаскару II (род. 1114). Формально их следовало бы причислить к астрономам, поскольку в то время математика считалась одной из астрономических техник. Их математические выкладки были разбросаны в отдельных главах в трудах по астрономии: никто не придавал им статуса самостоятельной науки.
Арьябхата утверждал, что свой труд «Арьябхатия» он создал в 23 года. Несмотря на краткость изложения, посвященный математике раздел его книги напичкан сведениями: буквенная система записи чисел, правила арифметики, методы решения простых и квадратных уравнений, тригонометрия (включая функции синуса и «обращенного синуса» 1 – cos θ). Также ему принадлежит превосходное по точности приближение 3,1416 для числа π.
Брахмагупта – автор двух книг: «Брахма-спхута-сиддханта» и «Кханда-кхадьяка». Первая – самая важная: это астрономический текст с углублением в математику, с арифметическими и словесными эквивалентами простой алгебры. Вторая книга в числе прочего включает замечательную интерполяционную формулу для вычисления синусов на основе небольшого числа известных табулированных значений этой функции: используются значения большего и меньшего углов, чем искомый.
Махавира исповедовал джайнизм и включил много положений этой религии в свой труд по математике, «Ганита-сара-самграха». Эта книга во многом повторяет труды Арьябхаты и Брахмагупты, но идет гораздо дальше и в целом намного сложнее. Она содержит описание дробей, перестановок и комбинаций, решение квадратных уравнений, теорему Пифагора и попытку вычислить периметр эллипса.
Бхаскара (известный также как «учитель») написал три известных труда: «Лилавати», «Биждаганита» и «Сиддханта-широмани» («Венец учения»). Согласно Фейзи, придворному поэту при могольском императоре Акбаре, дочь Бхаскары звали Лилавати. Отец решил составить ей гороскоп и вычислить точное время ее свадьбы. Чтобы придать своим манипуляциям наибольшую эффектность, он поместил дырявую чашку в таз с водой, так что в самый ответственный момент она должна была погрузиться на дно. Но Лилавати так низко наклонилась над водой, что жемчужинка с ее расшитого бусами платья отскочила и упала в чашку, закупорив дырку. Чашка так и не утонула, а это означало, что день свадьбы Лилавати никогда не наступит. Чтобы утешить дочь в ее горе, Бхаскара написал для нее труд по математике. Правда, легенда не уточняет, что подумала об этом сама девушка.

Древняя обсерватория Джантар-Мантар возле Джайпура. Сегодня очевидно, что дизайнер был прекрасным математиком
«Лилавати» посвящена сложным идеям арифметики и содержит метод девятки, при котором числа заменяют суммой составляющих их цифр, чтобы проверить результат вычислений. Там же приводятся правила проверки делимости на 3, 5, 7 и 11. Четко прописаны функции нуля как самостоятельной цифры. В «Биждаганите» мы находим способы решения уравнений. «Сиддханта-широмани» связана с тригонометрией: здесь есть таблицы синусов и различные тригонометрические соотношения. Репутация Бхаскари была столь прочной, что его книги переиздавали вплоть до начала XIX в.
ЧТО ДАВАЛА АРИФМЕТИКА ИМ
Самый древний из дошедших до нас математических текстов Китая – книга, отредактированная Чжан Цаном и датируемая примерно 100 г. н. э. Типичная задача такова: «Два с половиной пикуля риса были куплены за 3/7 ляна серебра. Сколько пикулей можно купить за 9 лянов?» Предполагаемое решение использует математический принцип, названный средневековыми математиками тройным правилом. В современных обозначениях, взяв за х неизвестное искомое количество, найдем:
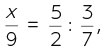
откуда x = 521/2 пикуля. Пикуль – мера веса, приблизительно равная 60,5 кг.
Назад: Индийские цифры
Дальше: Индийская система

