Рабочее определение вероятности некоего события – относительное число случаев, в которых оно происходит. Если речь о кости, у которой может одинаково часто выпасть любая из шести граней, вероятность выпадения каждой грани равна ¹/₆. Более ранние работы по вероятности основаны на подсчете количества вариантов появления каждого события и делении его на общее число возможностей.

Главной проблемой здесь были сочетания. Скажем, если взять колоду из шести карт, сколько в ней будет разных подмножеств по четыре карты? Один из способов – перечислить все эти подмножества: если у нас карты с достоинством 1–6, получится:

т. е. их всего 15. Но такой метод слишком громоздкий для большего количества карт, и здесь нужно нечто более систематическое.

Представим, что мы выбираем по одному элементу из подмножества. Первый можно выбрать шестью способами, второй только пятью (один использован), третий – четырьмя, четвертый – тремя. Общее число выборов в этом порядке равно 6 × 5 × 4 × 3 = 360. Но каждое подмножество сосчитано здесь 24 раза: начав с 1234, далее мы найдем 1243, 2134 и т. д. и получим 24 способа (4 × 3 × 2) переставить четыре объекта. Значит, точный ответ будет 360/24, т. е. 15. Этот аргумент показывает, что количество способов выбрать m объектов из общего числа n объектов равно:

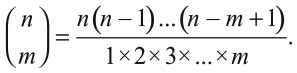
Это выражение называется биномиальным коэффициентом, потому что появляется и в алгебре. Если мы преобразуем его в таблицу, чтобы n-я строка содержала биномиальные коэффициенты

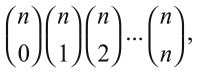
то результат будет выглядеть так.

В шестой (счет начинается с нуля) строке мы увидим числа 1, 6, 15, 20, 15, 6, 1.

Сравним с формулой

(x + 1)⁶ = x⁶ + 6x⁵ + 15x⁴ + 20x³ + 15x² + 6x + 1,

и мы видим, что те же числа появляются как коэффициенты. Это не совпадение.

Треугольник чисел назван треугольником Паскаля, потому что обсуждался Паскалем в 1655 г. Однако известен он был гораздо раньше: первое упоминание в древнеиндийском шастре «Чандас шастра» датируется примерно 950 г. Также его знали персидские математики Аль-Караджи и Омар Хайям (в современном Иране его называют треугольником Хайяма).

Треугольник Паскаля