Книга V «Начал» уводит нас в новом и неизведанном направлении от книг с первой по четвертую. Она непохожа на традиционную геометрию и, по сути, кажется бессмысленным набором слов. Как, например, понимать утверждение: «Если одни величины равно кратны по отдельности другим величинам, то и все первые совместно кратны всем вторым» (предложение 1 книги V)?

И дело не в изложении (которое я упростил). Доказательство ясно показывает нам, что имел в виду Евклид. Английский математик XIX в. Август де Морган изложил это понятным языком в своей книге по геометрии: «Десять футов десять дюймов в десять раз больше, чем один фут и один дюйм».

Чего же добивался Евклид? Пытался придать банальности вид теоремы? Или загадочной глупости? Вовсе нет. Для нас это темная материя, но она подводит к самой важной части «Начал» – общей теории отношений, построенной Евдоксом Книдским. Современные математики предпочитают работать с числами. Нам это привычнее, поэтому я часто буду переводить идеи древних греков на этот язык.

Евклид не избежал трудностей при работе с иррациональными числами. Кульминацией «Начал» – и, возможно, их главной темой – стало доказательство существования пяти правильных многогранников: тетраэдра, куба (гексаэдра), октаэдра, додекаэдра и икосаэдра. Евклид доказывает два допущения: больше не существует других правильных многогранников; эти пять действительно существуют: их можно построить геометрически, и их грани совпадают совершенно точно.

Два правильных многогранника, додекаэдр и икосаэдр, включают пятиугольники: у додекаэдра грани имеют форму пятиугольников, а каждые пять граней икосаэдра, собранные вокруг общего угла, образуют пятиугольник. Правильные пятиугольники связаны с тем, что Евклид называет «крайним и средним отношением». На отрезке АВ точка С располагается так, что отношение AB: АС равно отношению AC: BC. Меньшая часть отрезка относится к большей, как большая ко всему отрезку. Если вы нарисуете пятиугольник и впишете в него пятиконечную звезду, стороны последней будут относиться к сторонам пятиугольника точно так же.

В наши дни это отношение известно как золотое сечение. Оно равно (1 + √5) / 2, и это иррациональное число. Оно приблизительно равно 1,618. Древние греки смогли доказать, что оно иррационально, с помощью геометрических свойств пятиугольника. Значит, и Евклид, и его предшественники отдавали себе отчет в том, что для полного понимания свойств додекаэдра и икосаэдра им придется иметь дело с иррациональными числами.

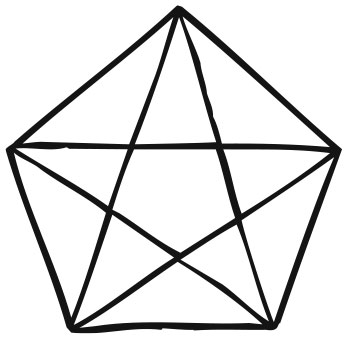
Отношение диагоналей к сторонам образует золотое сечение

Крайнее и среднее отношение (золотое сечение). Длина верхнего отрезка относится к длине среднего так же, как длина среднего – к нижнему

Таков традиционный взгляд, изложенный в «Началах». Дэвид Фоулер в своей книге «Математики Академии Платона» («The Mathematics of Plato’s Academy») утверждает, что это может толковаться иначе. Возможно, главной темой труда Евклида была теория иррациональных чисел, а рассуждения о правильных многогранниках – второстепенное приложение к ней. Действительно, мы можем интерпретировать текст Евклида по-разному, но одна особенность «Начал» говорит в пользу этой альтернативной теории. Основная часть теории чисел не нуждается в классификации правильных многогранников. Зачем же тогда Евклид включил их в свой труд? И только их прямая связь с теорией иррациональных чисел делает понятным такой ход.