Книга: Волновой принцип Эллиотта: Ключ к пониманию рынка
Назад: Глава 2. Нормы волнового принципа
Дальше: Часть 2. Практическое использование теории Эллиотта
Глава 3. Исторические и математические аспекты волнового принципа
Числовая последовательность Фибоначчи была открыта (в действительности открыта во второй раз) Леонардо Фибоначчи Пизанским, математиком, жившим в XIII в. Мы расскажем в общих чертах об этом удивительном человеке и затем более подробно остановимся на числовой последовательности (с технической точки зрения это последовательность, а не ряд), носящей его имя. Когда Эллиотт писал «Закон природы», он объяснял, что последовательность Фибоначчи является математической основой волнового принципа. (Чтобы подробнее ознакомиться с математическими закономерностями, стоящими за волновым принципом, можно обратиться к книге Вальтера Е. Уайта «Математические основы волновой теории» (Walter E. White. Mathematical Basis of Wave Theory), вышедшей в издательстве New Classic Library.)
Леонардо Фибоначчи Пизанский
«Темные века» были периодом почти полного культурного затмения в Европе. Они продолжались со времен падения Римской империи в 476 г. примерно до 1000 г., когда началось Средневековье. На протяжении этого периода математика и философия в Европе угасали, но расцветали в Индии и арабском мире, пока «Темные века» не распространились и на Восток. Когда Европа постепенно стала выходить из состояния стагнации, Средиземное море сделалось тем путем, по которому, направляя коммерческие потоки, неся новые математические и иные идеи из Индии и арабских стран, распространялась культура.

Во времена раннего Средневековья Пиза стала хорошо укрепленным городом-государством и процветающим торговым центром, чье портовое положение способствовало его дальнешему развитию. Кожи, меха, хлопок, шерсть, железо, медь, олово и пряности продавали и покупали за городскими стенами Пизы, где важнейшей валютой было золото. Порт был заполнен судами, иногда достигавшими веса в четыре сотни тонн и длины в восемьдесят футов. Основой пизанской экономики были выделка кож, кораблестроение и металлообработка. Пизанская политическая жизнь была весьма развита даже по нынешним стандартам. Главный магистрат республики, например, не получал денег за свою службу до тех пор, пока не истекал срок его полномочий, когда подводились итоги его деятельности и можно было проверить, заработал ли он свое жалование. Одним из проверяющих как раз и был Фибоначчи.
Родившийся между 1170 и 1180 гг. Леонардо Фибоначчи был сыном известного торговца и городского чиновника и, вероятнее всего, жил в одной из многочисленных башен Пизы. Башня служила мастерской, крепостью и семейным гнездом и была выстроена так, что в чужаков, если они приближались с недобрыми намерениями, из ее узких окон могли лететь стрелы, а на головы их литься кипящая смола. В то время когда жил Фибоначчи, колокольня, известная теперь как падающая Пизанская башня, еще только строилась. Она была последней из великих сооружений Пизы, поскольку кафедральный собор и крестильня были завершены несколькими годами ранее.
Школьником Леонардо познакомился с таможенной и коммерческой практикой того времени, в том числе и с выполнением операций с помощью абака, который широко использовали в Европе в качестве калькулятора, предназначенного для решения деловых задач. Хотя его родным языком был итальянский, он выучил еще несколько, в том числе французский, греческий и даже латынь, которую освоил в совершенстве.
Вскоре после того, как отец Леонардо был назначен таможенным чиновником в североафриканскую Боджию, он распорядился, чтобы сын присоединился к нему с целью завершения образования. Леонардо стал совершать многочисленные деловые поездки по Средиземноморью. После одного из путешествий в Египет он опубликовал свой знаменитый труд «Liber Abacci» («Книга исчислений»), в котором представил Европе одно из величайших математических открытий всех времен, называемое десятичной системой счисления, и в том числе нуль в качестве первой цифры числового ряда этой системы. Эта система, включающая знакомые всем символы 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, стала известна как индо-арабская и теперь используется повсеместно.
В рамках этой системы, предусматривающей разрядность числа, величина, представленная любым из символов, помещенным в ряд с другими символами, зависит не только от его номинальной величины, но и от положения в ряду. Так, 58 и 85 имеют различную величину. Хотя за тысячи лет до этого жители Вавилона и индейцы майя в Центральной Америке независимо друг от друга изобрели подобные системы счисления, имеющие разряды, их методы были неудобны в других отношениях. По этой причине вавилонская система, в которой впервые использовались ноль и разряд числа, так и не была принята математическими системами Греции или Рима, включавшими семь символов: I, V, X, L, С, D и М, с которыми были связаны величины, не имевшие разрядов. Сложение, вычитание, умножение и деление оказывались в такой безразрядной системе нелегкими задачами, особенно когда речь шла о больших числах. Парадоксально, но для решения этой проблемы римляне использовали очень древнее разрядное устройство, известное под названием абака. Поскольку этот инструмент основан на разрядности и использует ноль, он применялся как необходимое подспорье в римской вычислительной системе. На протяжении веков бухгалтеры и купцы полагались на него как на помощника в механизации стоявших перед ними задач. Фибоначчи после описания основного принципа абака в «Liber Abacci» начал использовать свою новую систему во время путешествий. Благодаря его усилиям, новая система с ее простым методом вычислений в конце концов прижилась в Европе. Постепенно римские цифры были заменены арабской числовой системой. Введение новой системы в Европе стало первым важным достижением в области математики за семь столетий со времен падения Рима. Фибоначчи не только дал возможность выжить математике в Средние века, но и заложил основу для великих открытий в области высшей математики и связанных с ней областях физики, астрономии и инженерии.
Хотя позже мир почти потерял Фибоначчи из виду, он, без сомнения, был выдающимся человеком своего времени. Его известность была настолько велика, что Фредерик II, сам ученый и исследователь, искал знакомства с ним и для этого организовал визит в Пизу. Фредерик II был императором Священной Римской империи, королем Сицилии и Иерусалима, потомком двух наизнатнейших семей Европы и Сицилии и самым влиятельным государем того времени. Он ратовал за абсолютную монархию и окружал себя пышностью, приличествующей императору.
Встреча Фибоначчи и Фредерика II произошла в 1225 г. и была весьма важным событием для Пизы. Император ехал во главе длинной процессии, состоящей из трубачей, придворных, рыцарей, чиновников и животных из императорского зверинца. Некоторые из проблем, поставленных императором перед великим математиком, рассмотрены в «Liber Abacci». По-видимому, Фибоначчи решил поставленные императором задачи, поскольку с тех пор всегда был желанным гостем при дворе. Когда в 1228 г. Фибоначчи подверг ревизии «Liber Abacci», он посвятил исправленное издание Фредерику II.
Будет почти преуменьшением сказать, что Леонардо Фибоначчи был величайшим математиком Средневековья. Его перу принадлежат три выдающихся математических труда: «Liber Abacci», опубликованная в 1202 и переизданная в 1228 г., «Practica Geometriae», изданная в 1220, и «Liber Quadratorium». Восхищенные граждане Пизы в 1240 г. подтвердили документально, что он был «благоразумным и ученым мужем», а совсем недавно Джозеф Гайз, старший редактор «Encyclopedia Britannica», заявил, что будущие исследователи со временем «воздадут должное Леонарду Пизанскому как одному из величайших в мире пионеров мысли». Его работы лишь теперь, спустя сотни лет, переведены с латыни на английский язык. Заинтересованные читатели могут обратиться к книге Дж. и Ф. Гайз «Леонард Пизанский и новая математика Средних веков», превосходному трактату, посвященному работам Фибоначчи и тем временам, когда они были написаны.
Несмотря на то что Фибоначчи был величайшим математиком Средневековья, его памяти посвящены лишь статуя, стоящая напротив Пизанской башни на другом берегу реки Арно, и две улицы, носящих его имя: одна в Пизе, а другая во Флоренции. Кажется странным, что среди несметных полчищ туристов, приходящих посмотреть на 179-футовую мраморную башню, лишь очень немногие хотя бы слышали имя Фибоначчи или видели его статую. Фибоначчи был современником Бонанны, архитектора, воздвигшего башню, строительство которой началось в 1174 г. Оба эти человека внесли свой вклад в мировую историю, но тот, чье влияние значительно превышало заслуги другого, остался почти неизвестным.
Последовательность Фибоначчи
В «Liber Abacci» поставлена задача, из решения которой возникает последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее до бесконечности, сегодня известная как последовательность Фибоначчи. Задача формулируется следующим образом:
«Сколько пар кроликов, помещенных в закрытое пространство, можно получить за один год от одной пары кроликов, если каждая пара приносит каждый месяц, начиная со второго, новую пару?»
В поисках решения мы обнаруживаем, что каждой паре, включая первую, требуется месяц для созревания, но, начав плодиться, она приносит ежемесячно новую пару. К началу второго месяца у нас по-прежнему только одна пара. Таким образом возникает последовательность 1, 1. Эта первая пара в конце концов удваивает свое количество во время второго месяца, так что в начале третьего месяца имеется две пары кроликов. После этого старшая пара приносит третью пару в следующем месяце, так что в начале четвертого месяца последовательность расширяется до 1, 1, 2, 3. Из этих трех пар приносят потомство две старшие пары, а самая молодая – нет, и количество пар кроликов доходит до пяти. В следующем месяце потомство приносят три пары, а последовательность расширяется до 1, 1, 2, 3, 5, 8 и т. д. На рис. 3–1 показано древо популяции кроликов, где видно, что популяция растет с экспоненциальным ускорением. Если продолжать последовательность в течение нескольких следующих лет, цифры станут астрономическими. Через 10 месяцев, например, нам пришлось бы возиться с 3544224848179261915075 парами кроликов. Последовательность Фибоначчи, возникающая из задачки про кроликов, обладает многими интересными свойствами. Например, отношения между ее членами, находящимися на одинаковом расстоянии друг от друга, почти не изменяются.
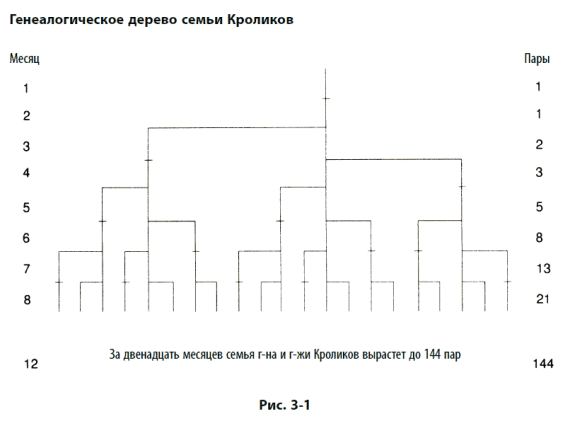
Сумма любых двух соседних чисел последовательности равна следующему за ними члену: так, 1 плюс 1 равно 2, 1 плюс 2 равно 3, 2 плюс 3 равно 5, 3 плюс 5 равно 8 и так далее до бесконечности.
Золотое соотношение
После нескольких первых чисел последовательности отношение любого ее члена к последующему приблизительно равно 0,618, а к предшествующему – 1,618. Чем больше порядковый номер члена последовательности, тем ближе отношение к числу фи (обозначается φ), являющемуся иррациональным числом и равному 0,618034… Отношение между членами последовательности, разделенными одним числом, примерно равно 0,382, а обратное ему число равно 2,618. На рис. 3–2 приведена таблица соотношений всех чисел Фибоначчи от 1 до 144.
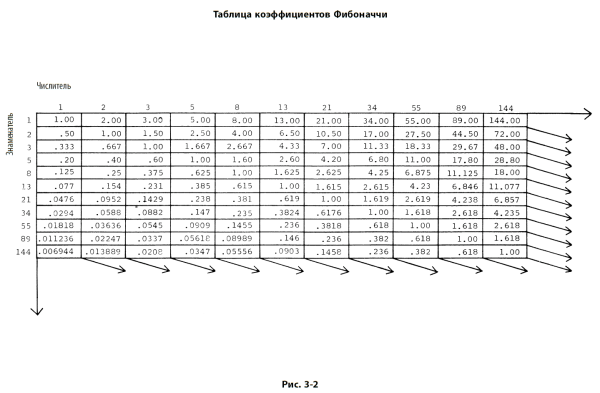
φ является единственным числом, которое, будучи прибавленным к 1, дает обратное себе число: 1 + 0,618 = 1: 0,618. Это родство процедур сложения и умножения приводит к следующей последовательности уравнений:
0,6182 = 1–0,618
0,6183 = 0,618 – 0,6182
0,6184 = 0,6182 – 0,6183
0,6185 = 0,6183 – 0,6184
или
1,6182 = 1 + 0,618
1,6183 = 1,618 + 0,6182
1,6184 = 1,6182 + 0,6183
1,6185 = 1,6183 + 0,6184
Некоторые взаимосвязанные свойства этих четырех основных коэффициентов перечислены ниже:
1,618 – 0,618 = 1
1,618 × 0,618= 1
1 – 0,618 = 0,382
0,618 × 0,618 = 0,382
2,618 – 1,618 = 1
2,618 × 0,382= 1
2,618 × 0,618= 1,618
1,618 × 1,618 = 2,618
Если любое число Фибоначчи, кроме 1 и 2, умножить на четыре и прибавить к определенному числу Фибоначчи, то получится другое число Фибоначчи, так что:
3 × 4 = 12; + 1 = 13
5 × 4 = 20; + 1 = 21
8 × 4 = 32; + 2 = 34
13 × 4 = 52; + 3 = 55
21 × 4 = 84; + 5 = 89
и т. д.
По мере роста новой прогрессии числа образуют третью последовательность, составленную из чисел, прибавленных к произведению четверки и числа Фибоначчи. Это делается возможным в связи с тем, что отношение между членами последовательности, отстоящими друг от друга на две позиции, равно 4,236, где число 0,236 является обратным к 4,236 и, кроме того, разностью между 4,236 и 4. Другие множители приводят к другим последовательностям, все они основаны на коэффициентах Фибоначчи.
Мы предлагаем вашему вниманию список некоторых дополнительных свойств, связанных с последовательностью Фибоначчи:
1. Никакие из двух последовательных чисел Фибоначчи не имеют общих делителей.
2. Если члены последовательности Фибоначчи пронумеровать как 1, 2, 3, 4, 5, 6, 7 и т. д., мы обнаружим, что, за исключением четвертого члена (число 3), номер любого числа Фибоначчи, являющегося простым числом (т. е. не имеющим иных делителей, кроме себя самого и единицы), также простое число. Сходным образом, за исключением четвертого члена последовательности Фибоначчи (число 3), все составные номера членов последовательности (т. е. те, что имеют как минимум два делителя за исключением себя самого и единицы), соответствуют составным числам Фибоначчи, что и показывает приведенная ниже таблица. Обратное не всегда оказывается верным.

3. Сумма любых десяти членов последовательности делится на одиннадцать.
4. Сумма всех чисел Фибоначчи до определенной точки последовательности плюс единица равна числу Фибоначчи, отстоящему на две позиции от последнего прибавленного числа.
5. Сумма квадратов любых последовательных членов, начинающихся с первой 1, всегда будет равна последнему (из данной выборки) числу последовательности, умноженному на следующий член.
6. Квадрат числа Фибоначчи минус квадрат второго члена последовательности в сторону уменьшения всегда будет числом Фибоначчи.
7. Квадрат любого числа Фибоначчи равен предыдущему члену последовательности, умноженному на следующее число в последовательности, плюс или минус единица. Прибавление и вычитание единицы чередуются по мере развития последовательности.
8. Сумма квадрата числа Fn и квадрата следующего числа Фибоначчи Fn + 1 равна числу Фибоначчи F2n + 1. Формула Fn2 + Fn + 12 = F2n + 1 применима к прямоугольным треугольникам, где сумма квадратов двух более коротких сторон равна квадрату самой длинной стороны. Справа приведен пример, использующий F5, F6 и квадратный корень из F11.
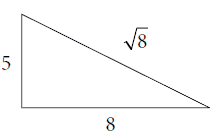
9. Формула, показывающая отношение между двумя наиболее распространенными иррациональными числами в математике π и φ:
Fn= 100 × π2 × φ(15 – n), где φ = 0,618…, n представляет собой порядковый номер в последовательности и Fn представляет сам по себе член последовательности. В данном случае число 1 представлено только один раз, так что F1 ≈ 1, F2 ≈ 2, F3 ≈ 3, F4 ≈ 5 и т. д.
Например, пусть n = 7. Тогда
F7 ≈ 100 × 3,14162 × 0,6180339(15 – 7) ≈
≈ 986,97 × 61803368 ≈
≈ 986,97 × 0,021129 ≈ 21,01 ≈ 21.
10. Одно из удивительных явлений, которое, насколько нам известно, до сих пор не упоминалось, состоит в том, что отношения между числами Фибоначчи равны числам, очень близким к тысячным долям других чисел Фибоначчи, при разности, равной тысячной доле еще одного числа Фибоначчи (см. рис. 3–2). Так, в направлении возрастания отношение двух идентичных чисел Фибоначчи равно 1, или 0,987 плюс 0,013; соседние числа Фибоначчи имеют отношение 1,618, или 1,597 плюс 0,021; числа Фибоначчи, расположенные с двух сторон от некоторого члена последовательности, имеют отношение 2,618, или 2,584 плюс 0,034, и т. д. В обратном направлении соседние числа Фибоначчи имеют отношение 0,618, или 0,610 плюс 0,008; числа Фибоначчи, расположенные с двух сторон от некоторого члена последовательности, имеют отношение 0,382, или 0,377 плюс 0,005; числа Фибоначчи, между которыми расположены два члена последовательности, имеют отношение 0,236, или 0,233 плюс 0,003; числа Фибоначчи, между которыми расположены три члена последовательности, имеют отношение 0,146, или 0,144 плюс 0,002; числа Фибоначчи, между которыми расположены четыре члена последовательности, имеют отношение 0,090, или 0,089 плюс 0,001; числа Фибоначчи, между которыми расположены пять членов последовательности, имеют отношение 0,056, или 0,055 плюс 0,001; числа Фибоначчи, между которыми расположено от шести до двенадцати членов последовательности, имеют отношения, которые сами являются тысячными долями чисел Фибоначчи, начиная с 0,034. Интересно, что в этом анализе коэффициент, связывающий числа Фибоначчи, между которыми располагаются тринадцать членов последовательности, снова начинает ряд с числа 0,001, с тысячной доли того числа, где он начался! При всех подсчетах мы действительно получаем подобие или «самовоспроизведение в бесконечном ряду», раскрывающее свойства «самой прочной связи среди всех математических отношений».
И наконец, заметим, что (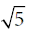
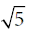
+ 1)/2 = 1,618 и (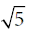
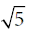
– 1)/2 = 0,618, где 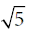
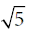
= 2,236. 5 оказывается наиболее важным для волнового принципа числом, а его квадратный корень является математическим ключом к числу φ.
Число 1,618 (или 0,618) известно как золотое отношение, или золотое среднее. Связанная с ним пропорциональность приятна для глаза и уха. Оно проявляется и в биологии, и в музыке, и в живописи, и в архитектуре. В своей статье, вышедшей в декабре 1975 г. в журнале Smithsonian Magazine, Вильям Хоффер сказал:
«…Отношение числа 0,618034 к 1 является математической основой формы игральных карт и Парфенона, подсолнуха и морской раковины, греческих ваз и спиральных галактик внешнего космоса. В основании очень многих произведений искусства и архитектуры греков лежит эта пропорция. Они называли ее «золотая середина».
Плодовитые кролики Фибоначчи выскакивают в самых неожиданных местах. Числа Фибоначчи, несомненно, часть мистической природной гармонии, которая приятна для ощущений, приятно выглядит и даже звучит приятно. Музыка, к примеру, основана на октаве в восемь нот. На фортепиано это представлено 8 белыми и 5 черными клавишами – в целом 13. Не случайно, что музыкальный интервал, приносящий нашему слуху самое большое наслаждение – это секста. Нота «ми» вибрирует в отношении 0,62500 к ноте «до». Это всего лишь на 0,006966 отстоит от точной золотой середины. Пропорции сексты передают приятные для слуха вибрации улитке среднего уха – органа, который тоже имеет форму логарифмической спирали.
Постоянное возникновение чисел Фибоначчи и золотой спирали в природе точно объясняет, почему отношение 0,618034 к 1 настолько приятно в произведениях искусства. Человек видит в искусстве отражение жизни, которая имеет в основании золотую середину».
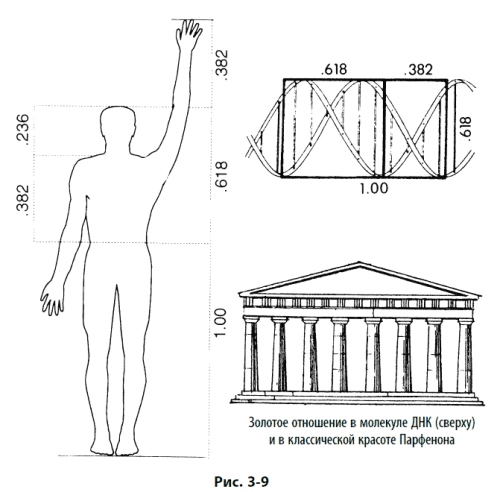
Природа использует золотое отношение в своих наиболее совершенных творениях – от таких мелких, как микроизвилины мозга и молекулы ДНК (см. рис. 3–9), до таких крупных, как галактики. Оно проявляется в таких различных явлениях, как рост кристаллов, преломление светового луча в стекле, строение мозга и нервной системы, музыкальные построения, структура растений и животных. Наука предоставляет все больше свидетельств того, что у природы действительно есть главный пропорциональный принцип. Кстати, вы держите эту книгу двумя из своих пяти пальцев, причем каждый палец состоит из трех частей. Итого: пять единиц, каждая из которых делится на три – прогрессия 5–3–5–3, подобная той, что лежит в основе волнового принципа.
Золотое сечение
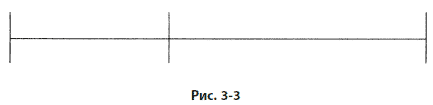
Любой отрезок может быть поделен таким образом, что отношение его меньшей части к большей окажется таким же, как и отношение большей части ко всему отрезку (см. рис. 3–3). Это отношение равно 0,618.
Золотое сечение встречается в природе повсеместно. Человеческое тело соответствует принципу золотого сечения (см. рис. 3–9) фактически во всем, начиная от внешних размеров и заканчивая чертами лица. «Платон в своем «Тимее» пошел так далеко, – говорит Питер Томпкинс, – что рассмотрел число φ и вывел пропорции золотого сечения – всеобъемлющее математическое соотношение и увидел в нем ключ ко всей природе космоса». В XVI столетии Иоганн Кеплер, говоря о золотом, или «Божественном», сечении, написал, что фактически оно описывает все созданное и символизирует Божественное творение «по своему подобию». Пупок делит человеческое тело по принципу золотого сечения. Для статистического усреднения используется число, примерно равное 0,618. Отношение остается верным отдельно для мужчин и отдельно для женщин, что есть символ творения «по своему подобию». Является ли и прогресс человечества творением «по своему подобию»?
Золотой прямоугольник
Стороны золотого прямоугольника имеют отношение 1,618 к 1. Чтобы построить золотой прямоугольник, начните с квадрата со сторонами, равными двум единицам, потом проведите линию от середины одной стороны квадрата к одной из его вершин, образующих противоположную сторону, как показано на рис. 3–4.
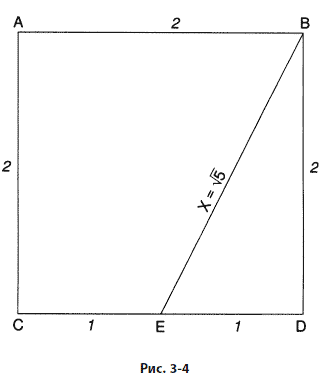
Треугольник EDB прямоугольный. Около 550 г. до Р.Х. Пифагор доказал, что квадрат гипотенузы (X) прямоугольного треугольника равен сумме квадратов двух других его сторон. В данном случае Х2 = 22 + 12, или Х2 = 5. Длина стороны ЕВ, таким образом, должна быть квадратным корнем из 5. Строя золотой прямоугольник, следующим шагом продлите отрезок СD и постройте на нем отрезок EG, равный квадратному корню из 5, или 2,236 единицы длины, как показано на рис. 3–5. В построенных таким образом прямоугольниках стороны связаны золотым коэффициентом. Таким образом, и прямоугольник AFGC, и прямоугольник BFGD золотые. Доказательство этого факта следующее:
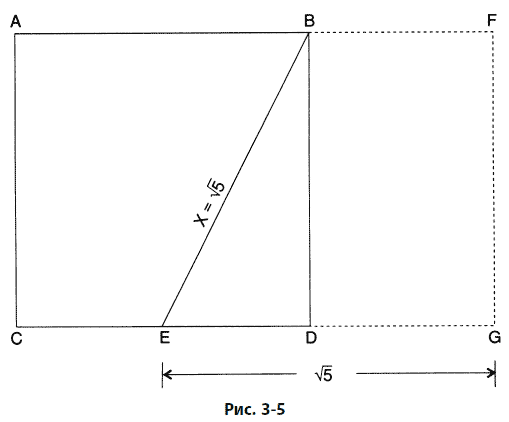
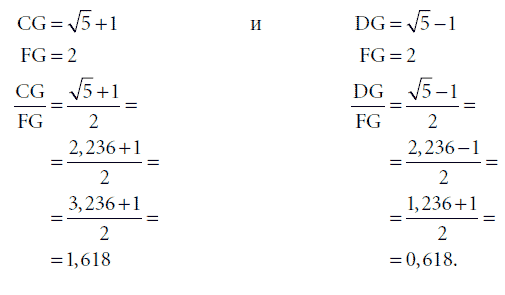
Поскольку стороны прямоугольников связаны золотым отношением, следовательно, эти прямоугольники, по определению, золотые прямоугольники.
Использование золотого прямоугольника в произведениях искусства чрезвычайно усиливает их привлекательность. Особенно сильно были очарованы золотым прямоугольником древние египтяне и греки, использовавшие его весьма часто. Не забывали о нем и художники Ренессанса, как, впрочем, и всех других наивысших моментов развития цивилизации. Большое значение золотому отношению придавал и Леонардо да Винчи. Он находил красивыми задаваемые им пропорции и говорил, что «если вещь выглядит неправильно, она не работает». Многие из его картин выглядели прекрасно, потому что он сознательно использовал золотой прямоугольник для усиления их привлекательности. Античные и современные архитекторы, и в особенности строители Парфенона в Афинах, неизменно придерживались правила золотого прямоугольника.
Очевидно, на человека, созерцающего форму, пропорции, связанные с числом φ, оказывают воздействие. Исследователи обнаружили, что люди находят такие формы эстетически привлекательными. Например, при проведении эксперимента людей просили выбрать из группы различных прямоугольников один. В общем случае выбор склонялся к прямоугольникам, форма которых была близка к золотому. Когда испытуемых просили произвольно разделить отрезок, они были склонны делить его в отношении φ. Окна, картинные рамы, здания, книги и кладбищенские кресты часто являются приближениями к золотому прямоугольнику.
Как и в случае золотого сечения, значение золотого прямоугольника не исчерпывается его красотой, но, по-видимому, обслуживает и функциональные задачи. Среди множества примеров наиболее удивительный состоит в том, что двойная спираль ДНК сама создает точные золотые прямоугольники, изгибаясь с правильными интервалами (см. рис. 3–9).
В то время как золотое сечение и золотой прямоугольник представляют собой статичные формы природной или рукотворной красоты и функциональности, наиболее ярким представлением эстетически приятного динамизма, упорядоченного роста или прогресса является одна из наиболее замечательных форм во Вселенной – золотая спираль.
Золотая спираль
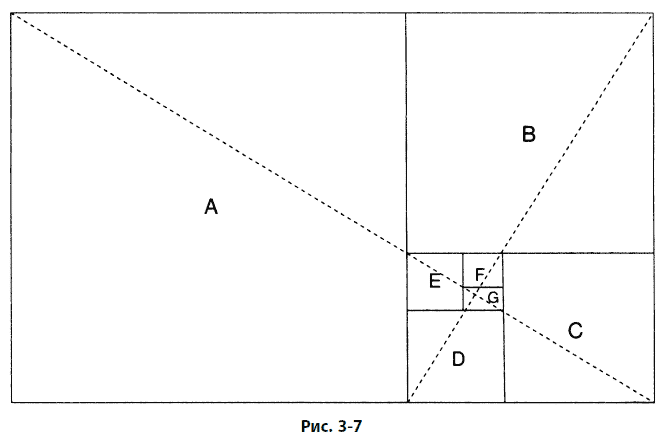
Для построения золотой спирали может быть использован золотой прямоугольник. Каждый золотой прямоугольник может быть поделен на квадрат и меньший золотой прямоугольник, как показано на рис. 3–6. Процесс такого деления теоретически может продолжаться бесконечно. Нарисованные в результате квадраты закручиваются внутрь, мы их пометили как A, B, C, D, E, F и С
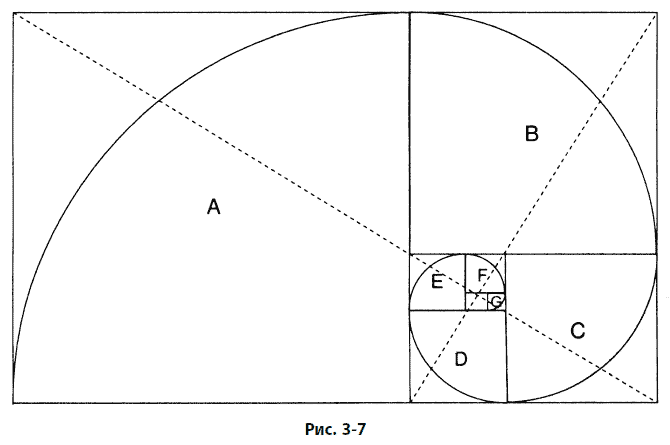
Пунктирные отрезки, которые сами имеют золотое отношение друг к другу, делят прямоугольник по диагоналям и указывают теоретический центр закручивающихся квадратов. Начав рядом с этой точкой, мы можем нарисовать спираль, показанную на рис. 3–7, соединив кривой точки пересечения закручивающихся квадратов в направлении их увеличения. По мере того как квадраты закручиваются внутрь и наружу, точки их соединения указывают путь золотой спирали.
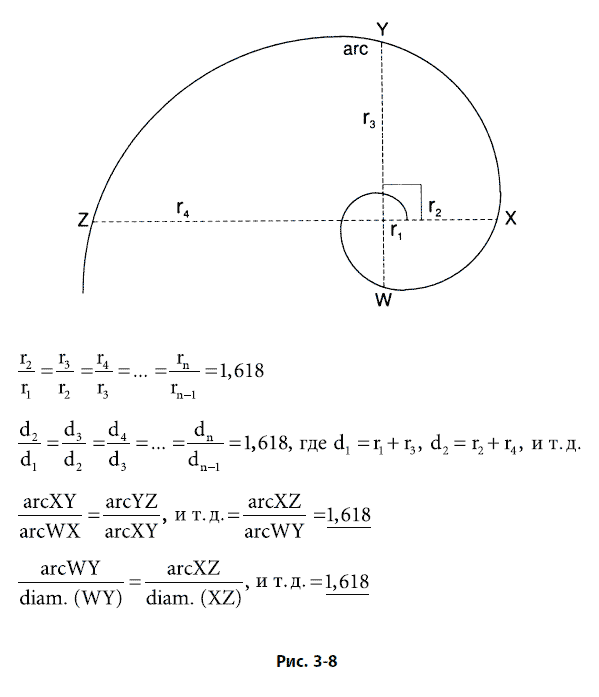
В любой точке золотой спирали отношение длины дуги к ее диаметру равно 1,618. Отношение диаметров и радиусов, отстоящих друг от друга на 90°, в свою очередь, равно 1,618, что и показано на рис. 3–8.
Золотая спираль, являющаяся логарифмической, или равноугольной, спиралью, не имеет границ и обладает постоянной формой. Из любой своей точки спираль может быть бесконечно продолжена как внутрь, так и наружу. Центр никогда не достигается, и наружу спираль простирается бесконечно. Ядро логарифмической спирали на рис. 3–8, если посмотреть на него под микроскопом, имело бы тот же вид, что и ее продолжение, если на него посмотреть с расстояния световых лет.
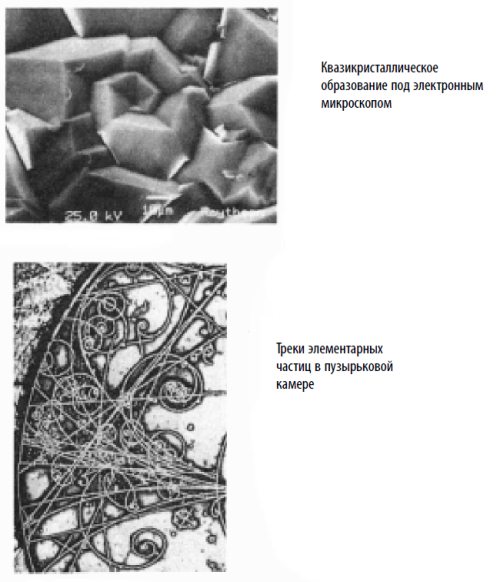
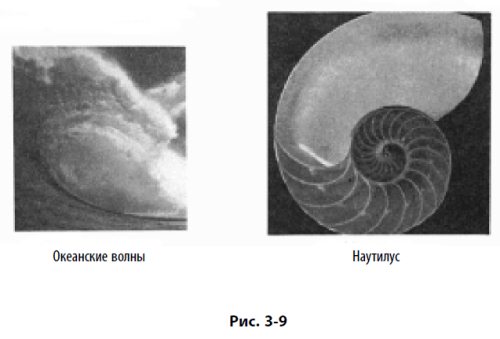
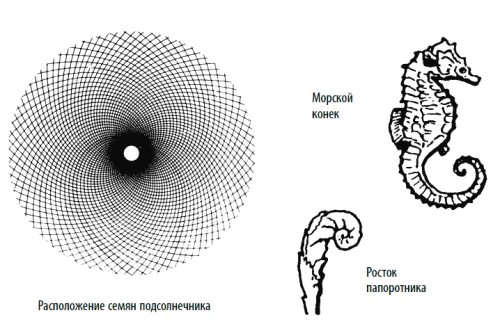
Если фигуры Евклидовой геометрии (может быть, за исключением эллипса) в типичном случае подразумевают статичность, спираль содержит движение: рост и уменьшение, развертывание и сжатие, прогресс и регресс. Логарифмическая спираль оказывается сущностным выражением явления естественного роста, обнаруживаемого во Вселенной повсеместно. Ее придерживаются и такие мелкие движения, как движение атомарных частиц, и такие огромные, как движение галактик. Как указывал Дэвид Бергамини в своей «Математике», написанной для серии «Time-Life Books’ Science Library», хвост кометы изгибается по направлению от Солнца по логарифмической спирали. Бактерии растут с ускорением, график которого имеет вид логарифмической спирали. Электронный микроскоп, наведенный на искусственный кристалл, обнаруживает логарифмические спирали. Еловые шишки, морские коньки, раковины моллюсков и улиток, океанские волны, папоротник, рога животных и расположение семечек подсолнуха или маргаритки – все это образует логарифмические спирали. Ураганы, водовороты и галактики внешнего космоса закручиваются в логарифмические спирали. Даже человеческий палец, составленный из трех костей, образующих по отношению друг к другу золотое сечение, принимает спиральную форму в согнутом виде. На рис. 3–9 мы видим отражение этого космического влияния во множестве форм. Миллионы лет и световые годы разделяют еловую шишку и спираль Млечного Пути, но устройство их одинаково: коэффициент 1,618, вероятно, есть первичный закон, управляющий динамикой природных явлений. Золотая спираль разворачивается перед нами как символ одного из величайших замыслов природы, как сила нескончаемого расширения и сжатия, статичный закон, управляющий динамическими процессами и основанный на коэффициенте 1,618 – отношении золотой середины.
Значение числа φ
На протяжении веков величайшие умы мира по достоинству оценивали значение этого вездесущего явления. История изобилует примерами ученейших людей, очарованных этой математической формулой. Пифагор в качестве символа Порядка выбрал пятиконечную звезду, в которой каждый отрезок находится в золотом отношении к следующему отрезку; знаменитый математик XVII в. Якоб Бернулли приказал, чтобы золотая спираль была выбита на его надгробии; Исаак Ньютон спал на кровати (сегодня она принадлежит фонду Gravity Foundation в Новом Бостоне), на изголовье которой была вырезана все та же золотая спираль. Первыми из известных приверженцев золотого отношения были строители пирамиды в Гизе, зафиксировавшие свое знание числа φ в ее конструкции почти 5000 лет назад. Египетские инженеры сознательно использовали золотое отношение в Великой Пирамиде, придав ее лицевым сторонам наклонную высоту, равную половине длины ее основания, умноженной на 1,618. Таким образом, вертикальная высота пирамиды равна квадратному корню из произведения половины ее основания на 1,618. По словам Питера Томпкинса, автора книги «Секреты Великой Пирамиды» (Harper & Row, 1971), «это отношение действительно показывает справедливость слов Геродота о том, что квадрат высоты пирамиды равен 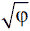
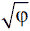
× 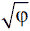
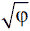
= φ, а площади ее фасадов 1 × φ = φ». Более того, применяя такие пропорции, математически искушенные египтяне (очевидно для того чтобы построить масштабированную модель Северного полушария) использовали числа π и φ в своих попытках нахождения квадратуры круга и кубатуры сферы (т. е. в попытках построить круг, равный по площади квадрату, и куб, равный по объему сфере). Увы, и спустя четыре тысячи лет эти задачи не были решены.
Несмотря на то что простое упоминание Великой Пирамиды может служить основанием для скептицизма (возможно, оправданного), не забывайте о том, что ее форма отражает те же чары, под обаянием которых находились столпы научной, математической, художественной и философской мысли, и среди них Платон, Пифагор, Бернулли, Кеплер, да Винчи и Ньютон. Строители пирамиды тоже были, несомненно, великолепными учеными, астрономами, математиками и инженерами. Они хотели сохранить золотое отношение на тысячелетия как нечто исключительно важное. То, что интеллектуалы такого калибра взяли на себя эту задачу (а к ним позже присоединились некоторые величайшие умы Древней Греции и эпохи Просвещения), само по себе поучительно. Что же касается причины, все, что у нас есть, – это предположения многочисленных авторов. Такие предположения, какими бы абсурдными они ни казались, имеют прямое отношение к нашим собственным наблюдениям. Высказывались догадки, что на протяжении веков после завершения ее строительства Великая Пирамида использовалась как храм, в котором получали посвящение те, кто доказали свое право на приобщение к великим тайнам мироздания. Лишь тот, кто мог подняться над незрелостью принятия вещей такими, какими они кажутся, и открыть, чем они на самом деле являются, мог участвовать в так называемых «мистериях», где раскрывались сложные «тайны» вечного истинного порядка.




Было ли среди этих тайн число φ? Томпкинс дает такое объяснение: «Египетские фараоны рассматривали φ не как число, но как символ творящей функции, или нескончаемого ряда воспроизведения. Для них оно представляло собой «жизненный огонь, разум, Логос, Слово, о котором говорится в Евангелии от Иоанна». Логос, а слово это греческое, определялся по-разному Гераклитом и более поздними языческими, еврейскими и христианскими философами: как смысл разумного устройства вселенского порядка, как имманентный закон природы, как животворящая сила, скрытая внутри вещей, как структурная сила, управляющая миром и пронизывающая его.
Вспомните, когда читаете столь величественные, но все еще смутные описания, что эти люди не могли ясно видеть то, что они чувствовали. У них не было графиков и волнового принципа, через которые могли бы явить себя естественные законы роста, и они делали то, что было в их силах, чтобы описать организационный принцип оформления природного мира, который они различали. Если эти древние философы были правы в том, что конструктивная универсальная сила правит миром и пронизывает его, почему бы ей не править и миром человеческим? Если повсеместно во Вселенной формы, включая человеческое тело, мозг и ДНК, являются отражением числа φ, почему бы и человеческой деятельности не отражать ее? Если φ – движущая сила Вселенной, почему бы ей не быть импульсом, стоящим за ростом производительной способности человечества? Если φ – символ функции созидания, почему бы ему не управлять творческой деятельностью человека? Если прогресс человечества зиждется на производстве и воспроизводстве «в бесконечном ряду», разве не было бы естественно, чтобы подобный прогресс обладал спиральной формой φ, и эта форма была заметна в изменениях оценки его производительных возможностей, т. е. на фондовом рынке? Умные египтяне, очевидно, поняли, что существуют сокрытые за кажущейся случайностью истины, относящиеся к порядку и росту во Вселенной. Современная «теория хаоса» возродила эту идею в 1980-х годах. Похожим образом, фондовый рынок, по нашему мнению, может быть правильно понят, только если рассматривать его таким, каков он есть, а не таким, каким он кажется незрелому поверхностному взгляду. Фондовый рынок – не случайная бесформенная масса, реагирующая на текущие новости, но вполне точная запись правильной структуры человеческого прогресса.
Сравните эту концепцию со словами астронома Вильяма Кингсланда, сказанными им в книге «Великая Пирамида в фактах и теориях», о том, что «египетская астрономия/астрология была глубокой эзотерической наукой, связанной с великим циклом человеческой эволюции». Волновой принцип объясняет великие циклы человеческой эволюции и раскрывает принципы их действия. Более того, он охватывает масштаб как макро-, так и микрокосма, в основании которых лежит парадоксальный принцип динамизма и вариативности внутри неизменной формы.
Именно эта форма придает Вселенной конструктивность и единство. Ничто в природе не предполагает, что жизнь неупорядоченна или бесформенна.
По-английски слово «вселенная» (universe) означает «единый порядок». Если у жизни есть форма, значит, мы не должны отвергать возможность того, что человеческий прогресс, будучи частью жизненной реальности, также имеет порядок и форму. Следовательно, и фондовый рынок, оценивающий производительную деятельность человека, будет иметь порядок и форму. Все технические подходы к пониманию фондового рынка опираются на основной принцип порядка и формы. Теория Эллиотта тем не менее идет дальше других. Она утверждает, что неважно, насколько мала или велика форма, основное ее строение всегда остается неизменным.
Эллиотт для второй монографии использовал название «Закон природы – Тайна мироздания» вместо старого названия «Волновой принцип» и применил свою теорию ко всем видам человеческой деятельности. Может быть, Эллиотт зашел слишком далеко, сказав, что волновой принцип – главная тайна мироздания, поскольку природа, по-видимому, создала бесчисленные формы и процессы, а не просто одну конструкцию. Тем не менее некоторые из величайших в истории ученых, о которых уже упоминалось, вероятно, согласились бы с Эллиоттом. Заслуживают доверия слова, что волновой принцип – одна из наиболее важных тайн мироздания.
Фибоначчи и спираль фондового рынка
Можем ли мы предполагать, что фондовый рынок стоит на той же математической основе, что и многие другие природные явления? Да. Как объяснял в своем финальном объединяющем заключении Эллиотт, ценовые волны развиваются по законам, управляющим всем порядком мироздания. Последовательность Фибоначчи регулирует число волн, формирующихся при движении фондовых индексов, приводя к базовому соотношению 5: 3, описанному в начале главы 1.
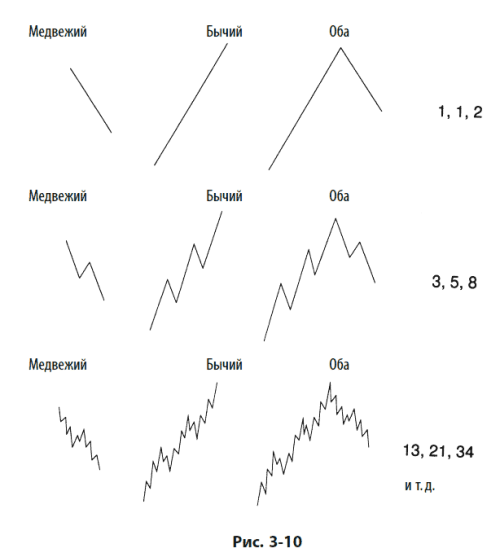
Как мы впервые показали на рис. 1–4, сущностная структура рынка отражает полную последовательность Фибоначчи. Простейшее выражение коррекции представляет собой прямолинейное снижение. Простейшее выражение импульса – прямолинейный подъем. Полный цикл состоит из двух линий.
На следующем уровне сложности, соответственно, возникают числа 3, 5 и 8. Как показано на рис. 3-10, эта последовательность может быть бесконечно продолжена. Тот факт, что волны приводят к последовательности чисел Фибоначчи, означает, что коллективно выражаемые человеческие эмоции привязаны к этому математическому закону природы.
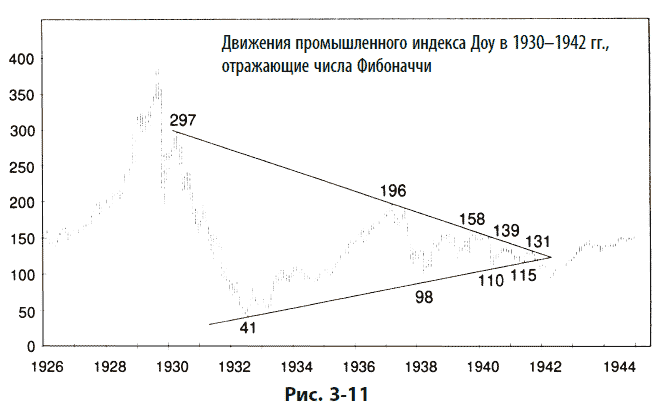
Давайте сравним образования, показанные на рис. 3-11 и 3-12. Каждое из них иллюстрирует естественный закон направленной внутрь золотой спирали и управляется отношением Фибоначчи. Отношение каждой волны к предыдущей равно 0,618. Фактически расстояния, выраженные в пунктах Доу, сами по себе отражают математический закон Фибоначчи. На рис. 3-11, показывающем последовательность 1930–1942 гг., колебания рынка покрывают примерно 260, 160, 100, 60 и 38 пунктов соответственно, что очень близко к убывающему списку коэффициентов Фибоначчи: 2,618, 1,618, 1,00, 0,618 и 0,382.
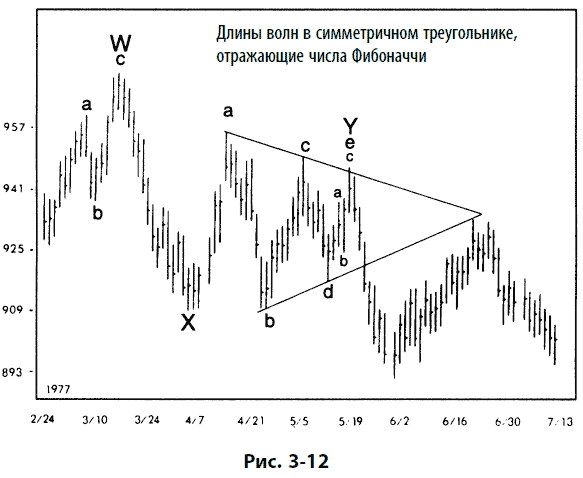
Начиная с волны Х 1977 г. в направленной вверх коррекции, показанной на рис. 3-12, колебания почти точно равны 55 пунктам (волна X), 34 пунктам (волны с а по с), 21 пункту (волна d), 13 пунктам (волна а волны е) и 8 пунктам (волна b волны е), а это сама по себе последовательность Фибоначчи. Общий чистый рост от начала и до конца составил 13 пунктов, и вершина треугольника лежит на уровне начала коррекции в 930, что также является уровнем пика последующего роста цен в июне. Если кто-то и рассматривает реальное количество пунктов в волнах как совпадение, то постоянное соотношение между волнами, равное 0,618, не может быть случайным. В главах 4 и 7 будет развита мысль по поводу возникновения коэффициента Фибоначчи в рыночных моделях.
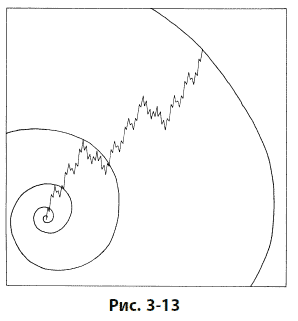
Отражает ли поведение фондового рынка, основывающееся на законах Фибоначчи, спиральный рост? И снова ответ – да. Идеализированная концепция движения фондового рынка Эллиотта, представленная на рис. 1–6, – превосходная основа для построения логарифмической спирали, что и показано с грубым приближением на рис. 3-13. В этом построении вершина каждой успешной волны более высокой степени является точкой, через которую проходит экспоненциальное расширение.
Эти два основных способа (последовательность Фибоначчи и спиральное развитие) социологической оценки производительной деятельности людей отражают и другие формы роста, встречающиеся в природе повсеместно. Таким образом, мы приходим к заключению, что все они подчиняются одному закону.
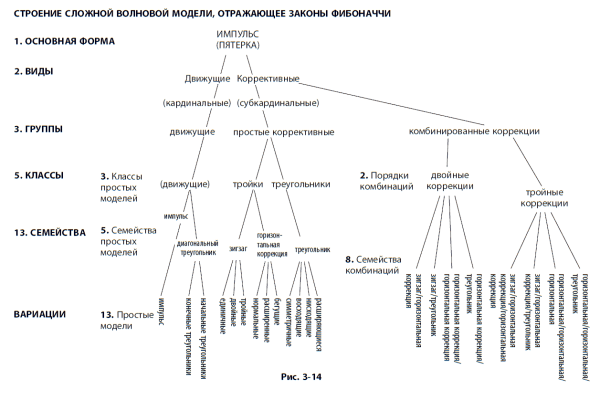
Математика Фибоначчи в структуре волнового принципа
Даже форма упорядоченной структуры сложной волны Эллиотта отражает последовательность Фибоначчи. Существует 1 основная форма: пятиволновая последовательность. Существует 2 вида волн: движущие (делящиеся на класс кардинальных волн, помечаемых цифрами) и коррективные (делящиеся на класс субкардинальных волн, помечаемых буквами). Существует 3 класса простых моделей волн: пятерки, тройки и треугольники (обладающие свойствами как троек, так и пятерок). Существует 5 семейств простых моделей: импульсы, диагональные треугольники, зигзаги, горизонтальные и треугольники. Существует 13 вариаций простых моделей: импульс, конечный диагональный треугольник, начальный диагональный треугольник, зигзаг, двойной зигзаг, тройной зигзаг, нормальная горизонтальная коррекция, расширенная горизонтальная коррекция, бегущая горизонтальная коррекция, сужающийся треугольник, нисходящий треугольник, восходящий треугольник и расширяющийся треугольник.
В коррективном виде волн различают две группы – простые и комбинированные коррекции, что доводит число групп до 3. Существует 2 класса коррективных комбинаций (двойные коррекции и тройные коррекции), что доводит общее число классов до 5. Допуская в комбинации лишь один треугольник и один зигзаг (что необходимо), мы получаем всего 8 семейств коррективных комбинаций: зигзаг/горизонтальная коррекция, зигзаг/треугольник, горизонтальная/горизонтальная, горизонтальная/треугольник, зигзаг/горизонтальная/горизонтальная, зигзаг/горизонтальная/треугольник, горизонтальная/горизонтальная/горизонтальная, горизонтальная/горизонтальная/треугольник, что доводит общее число семейств до 13. Общее число простых моделей и семейств комбинаций равно 21.
На рис. 3-14 изображено это дерево развития сложности. Перечисление перестановок в этих комбинациях или дальнейших вариаций меньшей важности внутри волн – вроде того, какая волна является растянутой, если таковая имеется, каким образом достигается чередование, содержится или нет в импульсе диагональный треугольник, какой тип треугольников входит в каждую комбинацию и т. д., – может послужить поводом для продолжения такой прогрессии.
В этом классификационном процессе можно усмотреть элемент надуманности, поскольку всякий способен придумать возможные вариации, приемлемые с точки зрения классификации. И все же тот факт, что принцип, имеющий отношение к последовательности Фибоначчи, по-видимому, сам отражает эту последовательность, заслуживает внимания.
Число φ и аддитивный рост
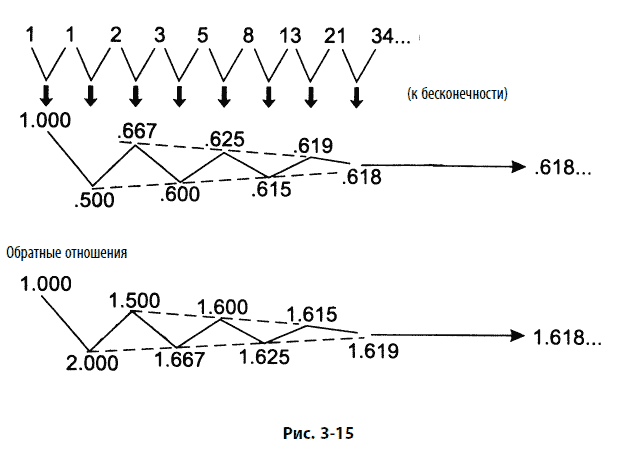
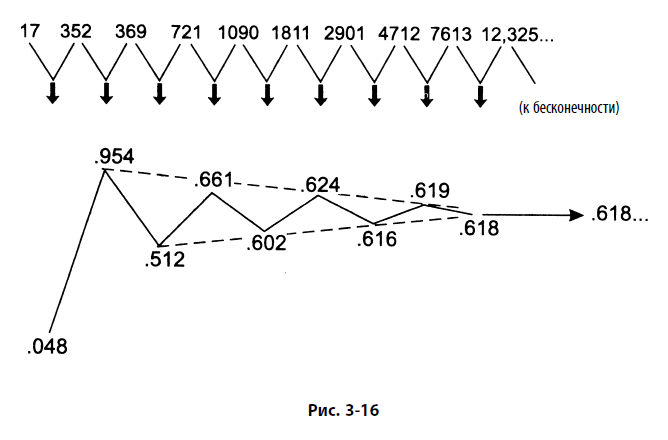
Как мы покажем в следующих главах, поведение рынка управляется золотым соотношением. Даже числа Фибоначчи появляются в рыночной статистике чаще, чем это допускает простая случайность. Тем не менее важно понимать, что хотя сами по себе числа все-таки имеют теоретический вес в главной концепции волнового принципа, именно соотношения оказываются основным ключом к моделям роста этого типа. Хотя на это редко указывают в литературе, коэффициент Фибоначчи возникает в аддитивной последовательности независимо от того, с каких двух чисел начинается последовательность. Последовательность Фибоначчи – базовая аддитивная последовательность, поcкольку она начинается с числа 1 (см. рис. 3-15), которое является начальной точкой математического роста. Однако мы можем с таким же успехом взять два случайно выбранных числа, таких как 17 и 352, и сложить их, чтобы получить третье, и т. д. По мере роста этой прогрессии соотношения между соседними членами последовательности всегда будут очень быстро стремиться к пределу, равному φ. Это соотношение становится очевидным к тому моменту, когда получен восьмой член (см. рис. 3-16). Таким образом, в то время как определенные числа, составляющие последовательность Фибоначчи, отражают идеальную прогрессию волн, возникающих на рынке, коэффициент Фибоначчи является фундаментальным законом прогрессии, в которой два предыдущих члена складываются для того, чтобы получить следующий. Вот почему этот коэффициент управляет таким большим количеством отношений в рядах данных, связанных с естественными явлениями роста и снижения, расширения и сжатия, подъемов и спадов.
В этом широком смысле волновой принцип предполагает, что закон, формирующий живые существа и галактики, присущ духу и деятельности людей en masse. Поскольку фондовый рынок самый точный барометр массовой психологии в мире, его данные дают прекрасную картину социально-психологических состояний и склонностей людей. Эта картина колеблющейся самооценки производительной деятельности выражает себя через определенные модели прогресса и регресса. Волновой принцип говорит, что прогресс человеческого рода (популярная оценка которого – фондовый рынок) не проявляется в виде прямой линии, случайного движения или циклов. Скорее прогресс «делает три шага вперед и два назад». Поскольку социальная активность человека связана с последовательностью Фибоначчи и спиральной моделью развития, по-видимому, она не исключение из наиболее распространенного во Вселенной закона упорядоченного роста. По нашему мнению, параллели между волновым принципом и другими природными явлениями слишком очевидны, чтобы их можно было отвергнуть как простой вздор. Учитывая баланс вероятностей, мы пришли к заключению, что существует вездесущий принцип, формирующий социальные явления, и что Эйнштейн знал, о чем рассуждал, говоря: «Господь не играет с Вселенной в кости». Фондовый рынок – не исключение, поскольку массовое поведение, несомненно, связано с законом, который может быть изучен и определен. Самый короткий путь к выражению этого принципа – простое математическое утверждение: коэффициент 1,618.
Поэт Макс Эрманн написал в «Desiderata»: «Ты Вселенной дитя, как деревья и звезды. Это место по праву твое. Думай, что хочешь, а мира вращенье проходит своим чередом». Жизнь подчинена определенным законам? Да. Те же законы управляют фондовым рынком? По-видимому, да.
Назад: Глава 2. Нормы волнового принципа
Дальше: Часть 2. Практическое использование теории Эллиотта

