Глава 4. Анализ отношений и временная последовательность Фибоначчи

Книга: Волновой принцип Эллиотта: Ключ к пониманию рынка

Назад: Часть 2. Практическое использование теории Эллиотта

Дальше: Глава 5. Долгосрочные волны и их современное состояние

Анализ отношений

Анализ отношений заключается в оценке пропорционального отношения одной волны к другой по времени и амплитуде. Ясно осознавая роль золотого коэффициента в рыночном цикле, состоящем из пяти шагов вверх и трех шагов вниз, можно предположить, что по завершении любой бычьей фазы последующая коррекция составила бы три пятых предшествующего роста как по времени, так и по амплитуде. Подобная простота встречается редко. Тем не менее соотношения волн часто соответствуют отношениям между членами последовательности Фибоначчи, что помогает сформировать правильный взгляд на каждую волну.

Изучение отношений волновых амплитуд на фондовом рынке зачастую может вести к открытиям настолько поразительным, что некоторые аналитики, применяющие волновой метод Эллиотта, прямо-таки одержимы ими. Хотя временные коэффициенты Фибоначчи по характеру не просты, годы анализа графиков фондовых индексов убедили авторов в том, что амплитуда (измеренная либо арифметически, либо в процентах) любой волны связана с амплитудой соседней волны, следующей за ней волны и/или внутренней волны одним из тех отношений, что связывают между собой числа Фибоначчи. Мы постараемся представить некоторые свидетельства этого и исследуем их совершенно беспристрастно, дав им возможность доказать или опровергнуть свою уместность.

Первые данные, отражающие временные и амплитудные соотношения на фондовом рынке, обнаруживаются в работах великого последователя теории Доу Роберта Ри. В 1936 г. в книге «История индексов» Ри представил обобщенную сводку рыночных данных, охватывающих, по теории Доу, 9 бычьих и 9 медвежьих рынков протяженностью в 36 лет, с 1896 по 1932 г. Вот как он обосновал необходимость представить эти данные, несмотря на то что в них не предполагалось никакой сиюминутной пользы:

«Несмотря на то, вносит или нет [этот обзор индексов] какой-то вклад в общую сумму исторических финансовых знаний, я определенно чувствую, что представленные статистические данные сэкономят другим исследователям многие месяцы работы… Следовательно, имеет смысл представить все статистические данные, которые мы собрали, а не только ту их часть, которая кажется полезной… Цифры, здесь представленные, возможно, не имеют большой ценности с точки зрения оценки будущих движений цены; как бы то ни было, это часть обобщенного исследования индексов, и такой подход заслуживает рассмотрения».

Обратите внимание на следующее наблюдение Ри:

«Итоговые цифры приведенной выше таблицы (в которой рассматривается лишь промышленный индекс) показывают, что 9 бычьих и медвежьих рынков, представленных в данном обзоре, охватывают 13 115 календарных дней. «Бычий» характер наблюдался на рынках в течение 8143 дней, в то время как оставшиеся 4972 дня приходились на медвежьи рынки. Отношение между этими цифрами говорит о том, что медвежьи рынки занимают 61,1 % времени, приходящегося на бычьи рынки».

И наконец:

«В колонке 1 показана сумма всех основных движений на каждом бычьем (или медвежьем) рынке. Очевидно, что эта цифра значительно выше, чем чистая разность между самой высокой и самой низкой цифрой любого из бычьих рынков. Например, бычий рынок, обсуждавшийся в главе II, начинался (для промышленного индекса) на отметке 29,64 и заканчивался на отметке 76,04, а разность, или чистый рост, составила 46,40 пунктов. Этот подъем происходил в четыре этапа, и первичные колебания составили 14,44; 17,33; 18,97 и 24,48 пунктов соответственно. Сумма этих подъемов составляет 75,22 пункта; эта цифра показана в колонке 1. Отношение суммарного роста к чистому подъему составило 1,621, что и дает процент, показанный в колонке 1. Предположим, что два трейдера были непогрешимы в своих операциях на рынке и что один из них купил акции в нижней точке бычьего рынка и, прежде чем продать, держал их вплоть до того дня, когда на рынке возникла самая высокая цена. Возьмем его доход за 100 %. Теперь представим, что другой трейдер купил акции в нижней точке и продавал на вершине каждого движения вверх, и снова откупал те же самые акции в нижней точке каждой второстепенной коррекции. Его прибыль составит 162,1 против 100 %, зафиксированных первым трейдером. Таким образом, в целом второстепенные реакции составили 62,1 % чистого подъема».

Так, в 1936 г. Роберт Ри, сам того не зная, открыл коэффициент Фибоначчи и ту функцию, которая связывает бычью и медвежью фазы как по времени, так и по амплитуде. К счастью, он почувствовал, что представленные данные важны; хотя в них и нет немедленной практической утилитарности, они могут оказаться полезными когда-нибудь потом. Сходным образом и мы чувствуем, что касательно коэффициентов многое еще только предстоит понять, и наше введение, которое лишь затрагивает поверхность проблемы, может оказаться важным и подвести будущих аналитиков к ответу на те вопросы, которые мы еще и не думали себе задавать.

С помощью анализа отношений было обнаружено большое количество точных ценовых отношений, часто появляющихся в волнах. Существует две категории таких отношений: соотношения размера коррекции и предшествующего ей импульса и соотношения однонаправленных волн внутри волновой модели.

Соотношения размера коррекции и предшествующего ей импульса

Время от времени возврат, возникающий при коррекции, выражается как соответствующий принципам Фибоначчи процент предыдущей волны. Как показано на рис. 4–1, резкая коррекция чаще всего стремится к возврату на 61,8 % или на 50 % предыдущей волны, особенно когда она проявляется как волна 2 импульса, волна В простого зигзага или волна Х во множественном зигзаге. Боковые коррекции чаще всего совершают возврат на 38,2 % предыдущей импульсной волны, особенно когда они проявляются как волна 4, что и показано на рис. 4–2.

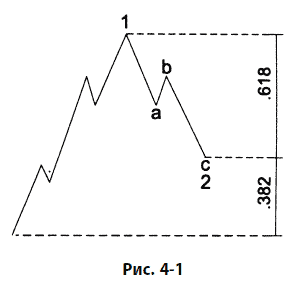
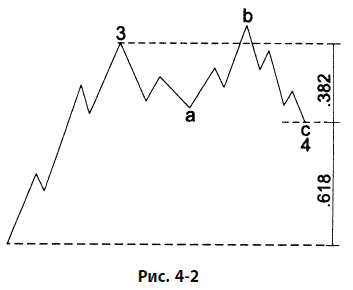
Коррекции могут иметь любой размер. Отношения, показанные на рис. 4–1 и 4–2, лишь тенденция. К сожалению, этому моменту большинство аналитиков уделяют чрезмерное внимание, поскольку измерить коррекцию не составляет труда. Однако значительно более точными и надежными оказываются отношения между волнами в импульсе, разворачивающимися в одном направлении, что и объясняется в следующем разделе.

Соотношения движущих волн

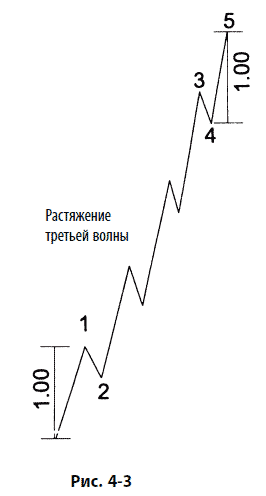
Как было замечено в главе 2, когда волна 3 растянута, волны 1 и 5 стремятся к равенству или отношению 0,618, как показано на рис. 4–3. Действительно, все три движущие волны проявляют тенденцию к взаимосвязи, выражающейся математическими законами Фибоначчи, будучи либо равными, либо связанными коэффициентами 1,618 или 2,618 (которые являются числами, обратными к 0,618 и 0,382). Эти соотношения импульсных волн обычно проявляются в процентных отношениях. Например, волна I, разворачивавшаяся с 1932 по 1937 г., поднялась на 371,6 %, в то время как волна III, имевшая место с 1942 по 1966 г., поднялась на 971,7 %, или в 2,618 раз выше. Чтобы обнаружить это отношение, необходимо использовать полулогарифмический масштаб. Конечно, на небольших степенях арифметический и процентный масштаб приводят к одним и тем же результатам, так что размеры волн в пунктах в каждом импульсе обнаруживают те же самые соотношения.

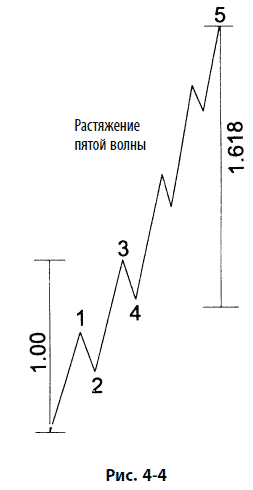
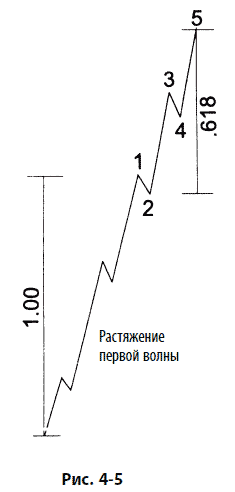
Другой типичный вариант развития состоит в том, что длина волны 5 иногда связана коэффициентом Фибоначчи с расстоянием от начала волны 1 до конца волны 3, как показано на рис. 4–4, демонстрирующем растяжение волны 5. Отношения 0,382 и 0,618 возникают, когда волна 5 не растянута. В тех редких случаях, когда растянутой оказывается волна 1, именно волна 2, что вполне оправданно, часто делит всю импульсную волну по правилу золотого сечения, как показано на рис. 4–5.

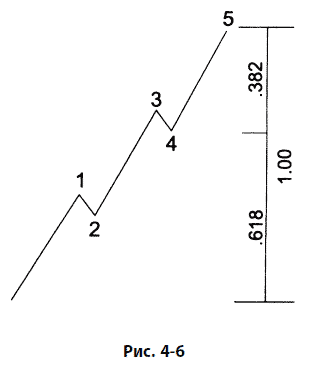
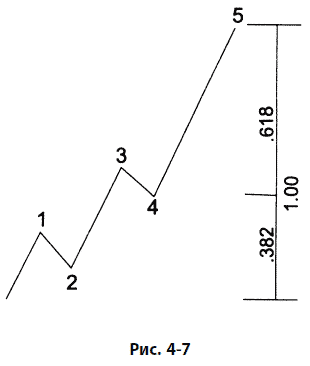
Вот обобщение, которое подводит итог некоторым из уже сделанных нами наблюдений: если волна 1 не оказывается растянутой, то волна 4 часто делит ценовой диапазон импульсной волны по правилу золотого сечения. В этих случаях последняя часть импульса равна 0,382 от общего пройденного ценой расстояния (если волна 5 не растянута), как показано на рис. 4–6; и 0,618, если волна 5 растянута, как показано на рис. 4–7. Примеры из реальной жизни приведены на рис. 6–8 и 6–9. Эта норма несколько расплывчата в том смысле, что конкретная точка внутри волны 4, которая приводит к такому делению, не зафиксирована. Это может быть начало волны, ее конец или точка противотрендового экстремума. Таким образом, для прогнозирования точки окончания волны 5 все это дает, в зависимости от обстоятельств, две или три близко расположенных цели. Эта норма объясняет, почему цель, определяемая для коррекции, следующей за пятой волной, часто указывается дважды: ее определяют по концу предыдущей четвертой волны и по коэффициенту коррекции 0,382.

Соотношения коррективных волн

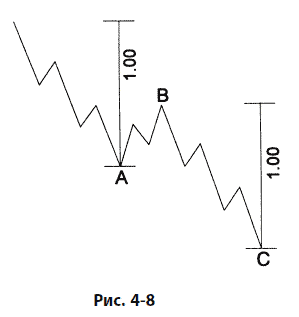
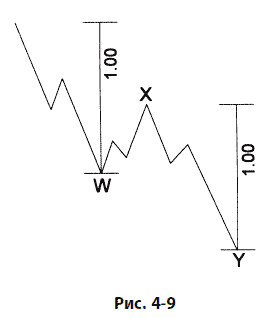
В зигзаге длина волны С обычно равна длине волны А, как показано на рис. 4–8, хотя нередко оказывается, что она составляет 1,618 или 0,618 длины волны А. То же самое наблюдение применимо и к отношению второго зигзага к первому в модели двойного зигзага, показанной на рис. 4–9.

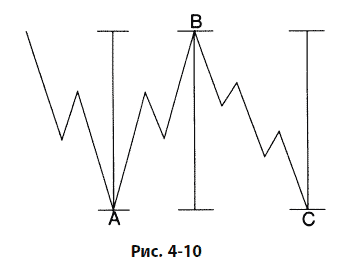
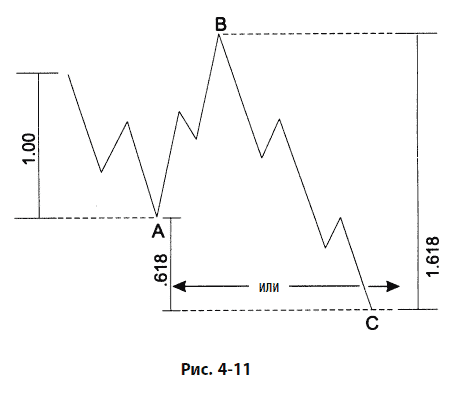
В нормальной горизонтальной коррекции волны А, В и С, конечно, примерно равны, как показано на рис. 4-10. В расширенной горизонтальной коррекции волна С часто в 1,618 раз длиннее волны А. Иногда волна С уходит дальше конца волны А на расстояние, равное 0,618 длины волны А. Все эти тенденции проиллюстрированы на рис. 4-11. В редких случаях волна С в 2,618 раз длиннее волны А. Волна В в расширенной горизонтальной коррекции иногда бывает в 1,236 или 1,382 длиннее волны А.

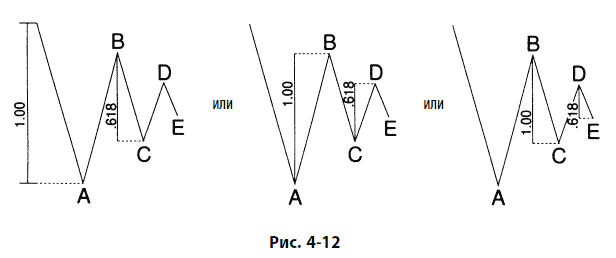
В треугольнике мы обнаруживаем, что по крайней мере две из волн, разделенных одной волной, в типичном случае связаны между собой коэффициентом 0,618. Таким образом, в сходящемся, восходящем и нисходящем треугольниках волна е = 0,618с, волна с = 0,618а или волна d = 0,618b, как показано на рис. 4-12. В расширяющемся треугольнике этот коэффициент равен 1,618. В редких случаях соседние волны могут быть связаны такими же соотношениями.

В двойных и тройных коррекциях чистое расстояние, которое покрывается в рамках одной простой модели, иногда связано с другой моделью равенством или (особенно если одна из троек – треугольник) коэффициентом 0,618.

И наконец, волна 4 довольно часто покрывает ценовой диапазон, равный или связанный отношением Фибоначчи с соответствующей волной 2. Как и в случае импульсных волн, эти отношения обычно проявляются в процентном масштабе.

Применение анализа отношений

Эллиотт был первым из тех, кто спустя несколько лет после выхода в свет книги Ри применил анализ отношений на практике. Он заметил, что изменение промышленного индекса Доу – Джонса в период с 1921 по 1926 г., охватывающий волны с первой по третью, составило 61,8 % размера пятой волны, продлившейся с 1926 по 1928 г. (1928 год был, согласно Эллиотту, истинной вершиной бычьего рынка). В точности те же отношения снова появились в направленных вверх пятых волнах в период с 1932 по 1937 г. (для справки см. рис. 2-11 и 2-12).

А. Гамильтон Болтон в 1957 г. в своем приложении к Bank Credit Analyst, посвященном волнам Эллиотта, дал такой ценовой прогноз, основанный на ожиданиях типичного поведения волны:

«Если рынок консолидируется еще в течение года или двух вблизи текущих ценовых уровней, то, как нам кажется, это позволит первичной волне V достичь сенсационных результатов, и в начале 1960-х гг. довести на волне активной покупки промышленный индекс Доу – Джонса до 1000 или более».

Затем в работе The Elliott Wave Principle – A Critical Appraisal, размышляя по поводу примеров, на которые ссылается Эллиотт, Болтон заявляет:

«Если бы рынок с 1949 г. до настоящего момента придерживался этой формулы, то подъем, продолжавшийся с 1949 по 1956 г. (361 пункт промышленного индекса Доу – Джонса) был бы закончен, когда к минимуму 1957 г. в 416 пунктов было бы добавлено 583 пункта (161,8 % от 361 пункта), или в целом 999 пунктов. В противном случае 361 пункт сверх 416 предусматривал бы 777 пунктов промышленного индекса Доу – Джонса».

Позже, когда Болтон писал приложение по волнам Эллиотта 1964 г., он делал такой вывод:

«Поскольку теперь мы успешно преодолели уровень 777 пунктов, похоже, что нашей следующей целью станет отметка в 1000».

Год 1966 показал, что эти утверждения были самым точным предсказанием в истории фондового рынка, когда в 3 часа дня 9 февраля был зарегистрирован максимум в 995,82 на часовом графике (внутридневный максимум был равен 1001,11). Таким образом, за шесть лет до этого события Болтон ошибся на 3,18 пункта, или менее чем на одну треть процента.

Несмотря на это замечательное предсказание, Болтон считал, как и мы, что анализ формы волны должен предшествовать выводам по поводу пропорциональных отношений. Действительно, при проведении анализа отношений чрезвычайно важно понимать и применять эллиоттовский метод подсчета и разметки волн, чтобы иметь возможность определить, от каких точек проводить измерения пропорциональных отношений. Отношения длин, основанные на уровнях истинных завершений моделей, вполне надежны; те, что основываются на неистинных ценовых экстремумах, обычно таковыми не оказываются.

Сами авторы тоже используют анализ отношений, и часто с успешными результатами. А.Дж. Фрост убедился в своей способности распознавать поворотные точки, поймав минимум Кубинского кризиса в октябре 1962 г. в час его возникновения. Он отослал телеграфом свои выводы в Грецию Гамильтону Болтону. Затем в 1970 г. в приложении к The Bank Credit Analyst он определил, что минимум медвежьего рынка для развивающейся коррекции циклической волны вероятнее всего появится на уровне, который будет ниже минимума 1966 г. на величину, равную снижению 1966 г., умноженному на 0,618, или на отметке в 572 пункта. Четыре года спустя часовой график промышленного индекса Доу – Джонса в декабре 1974 г. дошел до минимума в 572,20, после чего начался взрывной рост 1975–1976 годов.

Применение анализа отношений дает важные результаты и на более мелких степенях. Летом 1976 г. в отчете, опубликованном для Merrill Lynch, Роберт Пректер определил развивавшуюся тогда четвертую волну как редкий расширяющийся треугольник, а в октябре использовал коэффициент 1,618 для того, чтобы определить, что ожидаемый минимум восьмимесячной модели должен возникнуть на уровне 922 пунктов Доу. Минимум появился спустя пять недель на отметке 920,63 в 11 часов 11 ноября, дав старт пятиволновому ралли конца года.

В октябре 1977 г., за пять месяцев до событий, г-н Пректер вычислил вероятный уровень для главного дна 1978 г. как «744 или несколько ниже». Первого марта 1978 г. в 11 часов был зафиксирован минимум Доу ровно на отметке 740,30. В отчете, последовавшем спустя две недели после достижения индексом своего дна, вновь подтверждалась важность уровня в 740 пунктов:

«…Область 740 отмечает тот момент, где коррекция 1977–1978 гг. в точности равна длине всего бычьего рынка (в пунктах), поднимавшегося с 1974 по 1976 г., умноженной на 0,618. С математической точки зрения, мы можем утверждать, что 1022 – (1022 – 574) × 0,618 = 744 (или, используя истинную вершину 31 декабря, 1005 – (1005 – 572) × 0,618 = 737). Во-вторых, область 740 отмечает точку, в которой коррекция 1977–1978 гг. ровно в 2,618 раз длиннее предшествующей коррекции 1975 г., продолжавшейся с июля по октябрь, так что 1005 – (885–784) × 2,618 = 742. В-третьих, связывая цель с внутренними компонентами снижения, мы обнаруживаем, что длина волны С в 2,618 раз больше длины волны А, если дно волны С приходится на отметку 746. Даже соотношения волн, отмеченные в отчете апреля 1977 г., указывают на отметку 740 как на наиболее вероятный уровень разворота. Итак, при таком стечении обстоятельств подсчет волн безупречен. В настоящее время рынок, вероятно, стабилизируется. Последний приемлемый целевой уровень, если принять тезис о циклической степени бычьего рынка, достигнут 1 марта (740,30 пунктов). Именно про такие моменты Эллиотт говорил, что рынок “должен это принять или сломать”».

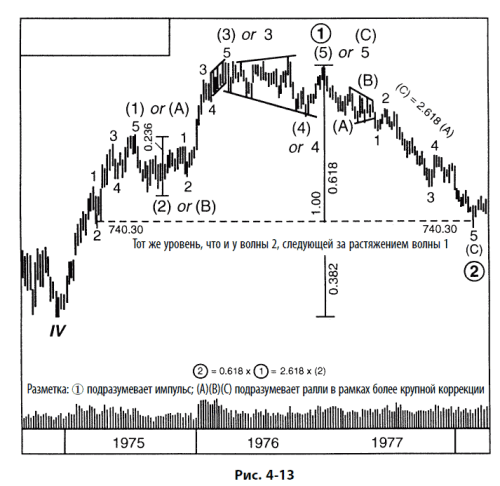
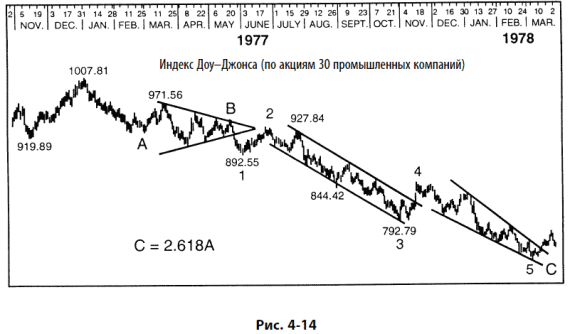
Здесь воспроизведены три графика из этого отчета. Это рис. 4-13 (с некоторыми дополнительными пометками, заменяющими текстовые комментарии), 4-14 и 4-15. Они иллюстрируют волновую структуру от первичной до мельчайшей степени. Даже для этой ранней даты 740,30 кажется твердо установленным минимумом первичной волны

в циклической волне V.

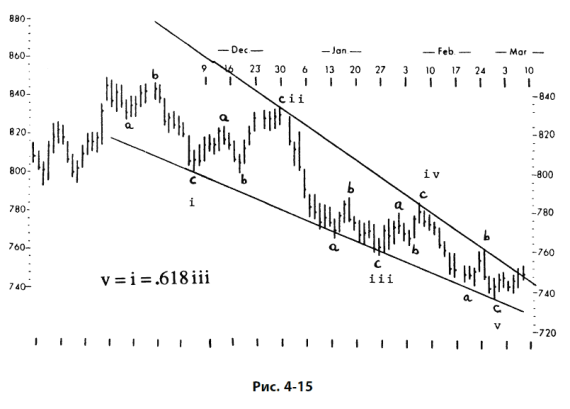
Важность уровня в 740 пунктов была отмечена и раньше. Минимум 1974 г. в 572,20 пункта лежит ровно на 423,60 пункта ниже пика 1966 г. в 995,82 пункта, а уровень 740,30 находится примерно на 261,80 пункта ниже уровня 1004,65, являющегося истинной вершиной 1976 г. Оба эти расстояния оказываются выражениями отношений Фибоначчи. Г-н Пректер и позже обсуждал уровень в 740 пунктов:

«Конечно, не случайно, что важность уровня в 740 пунктов имеет доказательства и в прошлом. В 1961 г. внутридневной пик Доу в 741,30 пункта сопровождался самым высоким отношением цена/прибыль (Р/Е) в истории рынка; в 1966 г. внутридневной минимум в 735,74 обозначил конец первого этапа падения к минимуму циклической волны IV медвежьего рынка (точка, отметившая 61,8 % всего снижения циклической волны IV); в 1963, 1970, 1974 и 1975 г. пробои уровня 740 пунктов в каждом из направлений сопровождались мощным движением рынка; в 1978 г. уровень в 740 пунктов соответствует долгосрочной линии поддержки тренда. Более того, волновой принцип утверждает, что всякая коррекция на рынке ограничена дном предыдущей четвертой волны меньшей степени. Однако когда первая волна в пятиволновой последовательности растянута, граница последующей коррекции часто оказывается дном второй волны этой пятиволновой последовательности. В свете этой нормы волнового анализа недавний минимум 1 марта, возникший на уровне 740,30, был уровнем защитной остановки. Проверка прошлых часовых данных, напечатанных в Wall Street Journal, обнаруживает, что достижение 25 марта 1975 г. промышленным индексом Доу – Джонса своего дна на отметке в 740,30 завершило откат второй волны». [См. примечание на рис. 4-13.]

В дополнение к традиционным эллиоттовским методам прогнозирования г-н Пректер начал исследовать математические свойства волн с точки зрения времени и цены. Он обнаружил, что движущие волны кратны целым числам, а коррективные волны кратны коэффициентам Фибоначчи. Этот подход недавно обсуждался в нескольких отчетах для Merrill Lynch.

Несомненно, некоторым покажется, что мы расхваливаем самих себя. Однако мы надеемся, что успех, которого мы добились с помощью методов Эллиотта, вдохновит других побороться за такие же достижения в использовании этого подхода. Насколько мы можем судить, лишь волновой принцип позволяет делать прогнозы с такой точностью. Конечно, и нас постигали неудачи, но, как бы то ни было, мы чувствуем, что любые недостатки волнового подхода Эллиотта в прошлом были сильно преувеличены и что когда ожидания относительно рынка не оправдываются, волновой принцип заблаговременно предупреждает аналитика и дает ему возможность выбрать следующий наиболее вероятный путь и избежать потерь, позволив самому рынку диктовать способ действий.

Мы обнаружили, что заранее определенные ценовые цели полезны в том отношении, что если разворот возникает вблизи цели и подсчет волн приемлем, то достигнута вдвойне существенная точка. Если рынок игнорирует этот уровень или пробивает его, вы получаете сигнал о том, что следует ожидать достижения следующего вычисленного уровня. Поскольку следующий уровень часто оказывается в достаточной степени удаленным, это может стать чрезвычайно важной информацией. Более того, цели основываются на наиболее приемлемом подсчете волн. Таким образом, если они не достигаются или значительно превышаются, во многих обстоятельствах вы будете вынуждены своевременно пересмотреть свой предпочтительный подсчет и найти более привлекательную интерпретацию. Этот подход помогает вам быть на один шаг впереди и не сталкиваться с неприятными сюрпризами. Следует помнить все разумные интерпретации текущего поведения цен и использовать анализ отношений, чтобы получить дополнительные указания на то, какая из них актуальна.

Множественные волновые отношения

Не забывайте, что на рынке в одно и то же время действуют тренды всех степеней. Таким образом, в любой данный момент рынок содержит несколько отношений Фибоначчи, появление которых имеет отношение к разворачивающимся волнам различных степеней. Из этого следует, что прогнозируемые уровни, порождающие несколько отношений Фибоначчи, с большей вероятностью отмечают разворот, чем уровень, создающий лишь единственное такое отношение.

Например, если возврат первичной волны

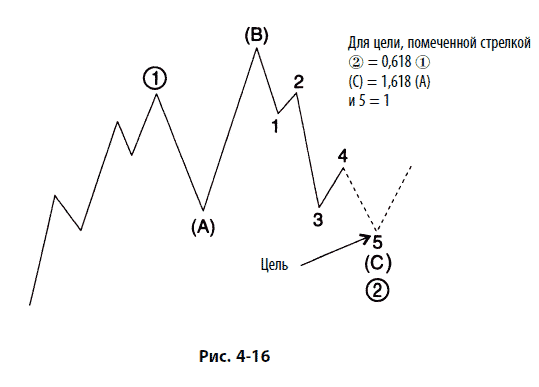
на 0,618 первичной волны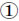

дает некоторую цель и в ее рамках коэффициент 1,618 для волны (А) промежуточной степени в неправильной коррекции дает ту же самую цель для промежуточной волны (С), а в ее рамках коэффициент 1,00 для малой волны 1 снова дает ту же цель для малой волны 5, тогда у вас есть мощный аргумент в пользу того, что следует ожидать разворота на этом заранее рассчитанном ценовом уровне. Рис. 4-16 иллюстрирует этот пример.

На рис. 4-17 изображена идеализированная волна Эллиотта, дополненная каналом, параллельным тренду. Она была построена в качестве примера нахождения ценовых целей волн. В ее рамках обнаруживаются следующие восемь отношений:

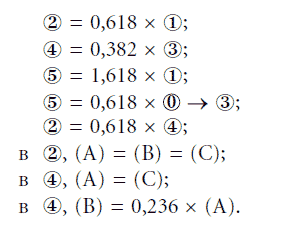
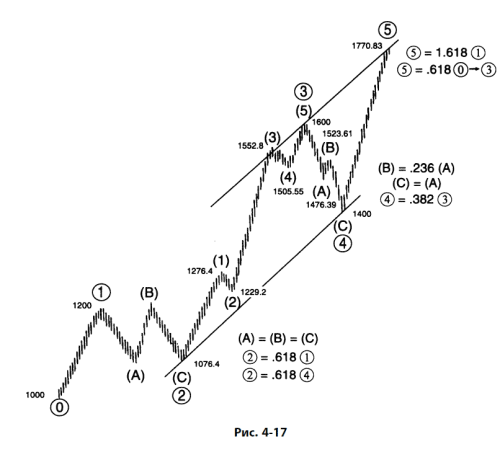
Если законченный метод анализа отношений успешно войдет в набор основных принципов, прогнозирование с помощью волнового принципа Эллиотта станет более научным. Тем не менее он навсегда останется задачей по определению вероятностей, а не твердых фактов. Закон природы, управляющий жизнью и ростом, хотя и остается непреложным, тем не менее допускает огромную вариативность определенных исходов, и рынок здесь не исключение. И все же мы уверены, что сравнение ценовых длин волн часто подтверждает, и зачастую с удивительной точностью, что отношения Фибоначчи – ключевой указатель уровня завершения волны.

С благоговейным вдохновением, но без удивления мы обнаружили, например, что подъем, имевший место с декабря 1974 г. по июль 1975 г., покрыл немногим более 61,8 % предыдущего медвежьего снижения 1973–1974 гг. и что снижение на рынке 1976–1978 гг. покрыло в точности 61,8 % предыдущего роста, происходившего с декабря 1974 г. по сентябрь 1976 г. Несмотря на постоянные подтверждения важности коэффициента 0,618, в первую очередь мы должны полагаться на форму, рассматривая анализ отношений как свидетельство, подтверждающее или опровергающее то, что мы видим в моделях изменения цен. В отношении анализа отношений Болтон советовал всегда использовать наиболее простые интерпретации. Дальнейшие исследования могут продвинуть дело вперед, поскольку анализ отношений пока находится в зачаточном состоянии. Мы надеемся, что те, кто потрудятся над проблемой анализа отношений, внесут значительный вклад в волновой анализ.

Временная последовательность Фибоначчи

Нет надежного способа прогнозирования времени завершения волновых моделей. Эллиотт говорил (например, по отношению к трендовым каналам), что временной фактор часто «сообразуется с моделью», и здесь лежит его главное значение. Однако зачастую длительности волн сами отражают отношения Фибоначчи. Исследование временных отрезков с точки зрения чисел Фибоначчи, по-видимому, выходит за рамки упражнения в нумерологии, поскольку длительности волн соответствуют отношениям Фибоначчи с замечательной точностью. Они дают аналитику дополнительную перспективу, указывая на возможные моменты разворотов, особенно если соответствуют ценовым целям и подсчету волн.

В «Законе природы» Эллиотт приводит следующие примеры временных интервалов Фибоначчи между важными разворотными точками на рынке:

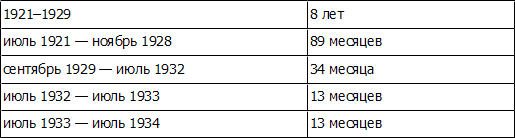
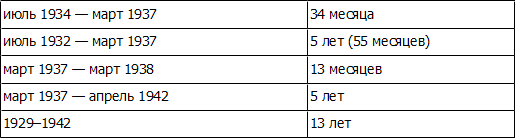
Ричард Рассел 21 ноября 1973 года в Dow Theory Letters дал несколько дополнительных примеров временных периодов Фибоначчи:

В своей монографии 1968 г., посвященной волновому принципу Эллиотта, Вальтер Е. Вайт заключает, что «следующая важная нижняя точка может быть достигнута в 1970 г.». В подтверждение этого он приводит следующую последовательность Фибоначчи: 1949 + 21 = 1970; 1957 + 13 = 1970; 1962 + 8 = 1970; 1965 + 5 = 1970. Май 1970 г., конечно, отметил нижнюю точку наиболее ожесточенного спада за 30 лет. Взятые in toto, эти длительности кажутся больше, чем просто совпадением.

Временная прогрессия, начинающаяся с возможного истинного максимума 1928 г. и номинального максимума 1929 г. последнего суперцикла, также приводит к замечательной последовательности Фибоначчи:

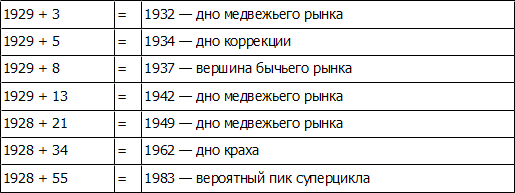
Сходная серия начинается с возможной истинной вершины 1965 г. и номинальной вершины третьей циклической волны текущего суперцикла:

Таким образом, мы можем предсказать интересные возможности в отношении разворотных точек промышленного индекса Доу – Джонса в близком будущем. Эти возможности исследуются далее в главе 8.

Применяя временные периоды Фибоначчи к рыночным моделям, Болтон заметил, что это часто приводит к «бесконечной путанице». Несмотря на такую оговорку, он с успехом указал в той же самой книге, опубликованной в 1960 г., что, основываясь на последовательности Фибоначчи, 1962 или 1963 год должен дать важную разворотную точку. Как мы теперь знаем, 1962 год стал свидетелем сильнейшего медвежьего рынка и минимума первичной волны ④, который предшествовал непрерывному подъему, длившемуся почти четыре года.

Открытое Робертом Ри временное соотношение между бычьим и медвежьим рынками, дополняющее этот тип анализа временной последовательности, также можно использовать для прогнозирования. В работе для Merrill Lynch Роберт Пректер заметил в марте 1978 г, что «17 апреля отмечает день, когда истечет 1931 рыночный час снижения А – В–С, или 61,8 % 3124 рыночных часов волн (1), (2) и (3)». Пятница 14 апреля отмечена верхним пробоем модели «перевернутая голова и плечи» на графике индексом Доу – Джонса. В понедельник, 17 апреля, был отмечен взрывной рост торгового оборота, который достиг 63,5 миллиона акций (см. рис. 1-18). Хотя на этот раз проекция не соответствовала минимуму, она все же отмечала точный день, когда предшествующее психологическое давление медведей исчезло с рынка.

Теория Беннера

Сэмюэл Т. Беннер занимался производством чугуна, однако был разорен в 1873 г. на волне финансового кризиса, последовавшего за Гражданской войной. Он стал фермером в штате Огайо и в качестве хобби предпринял статистическое исследование ценовых движений. Беннер хотел обнаружить закономерность в повторяющихся подъемах и спадах бизнеса. В 1875 г. Беннер написал книгу, озаглавленную «Экономические пророчества будущих взлетов и падений цен». Прогнозы, содержащиеся в его книге, по большей части основаны на циклах цен чугуна и на повторяемости финансовой паники. Прогнозы Беннера за долгие годы показали свою замечательную точность, а он сам как статистик и прогнозист стяжал завидную славу. Даже сегодня графики Беннера вызывают интерес исследователей циклов, и время от времени их можно встретить в печати, иногда без указания авторства.

Беннер заметил, что подъемы экономики возникают в рамках повторяющейся 8–9–10-годичной модели. Если мы приложим такую модель к максимумам промышленного индекса Доу – Джонса за последние 75 лет, начиная с 1902 г., то получим следующие результаты. Эти даты не являются проекциями, основанными на прогнозах, сделанных ранее Беннером, – они получаются в результате применения модели повторения 8–9–10 к историческим данным.

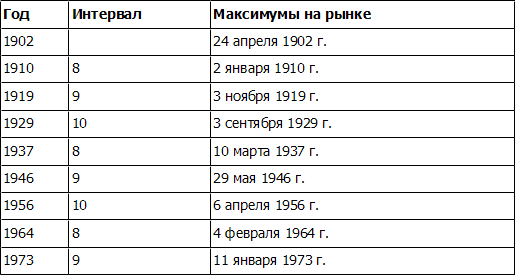
В отношении нижних точек экономики Беннер отметил две временные последовательности, показывающие, что рецессии («плохие времена») и депрессии («паника») имеют тенденцию к чередованию (что не удивительно, учитывая правило чередования Эллиотта). Комментируя моменты паники, Беннер сделал наблюдение, что 1819, 1837, 1857 и 1873 г. были паническими годами, и показал на своем «паническом» графике, что они отражают повторяющуюся модель 16–18–20, что приводит к неравномерной периодичности этих повторяющихся событий. Хотя к рецессиям, или «плохим временам», он применил модель 20-18-16, менее важные минимумы фондового рынка, по нашему мнению, также следуют модели 16–18–20, как и главные панические минимумы. Применив модель 16–18–20 к чередующимся минимумам фондового рынка, мы получим точное совпадение, что и иллюстрирует циклический график Беннера – Фибоначчи (рис. 4-18), впервые опубликованный в 1967 г. в приложении к Bank Credit Analyst.

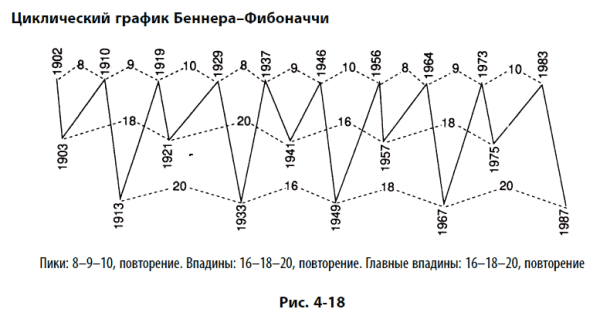
Обратите внимание на то, что последним моментом, когда конфигурация цикла оказывалась той же, что и теперь, был период 1920-х годов, и это было последнее появление пятой волны Эллиотта циклической степени.

Такая формула, основывающаяся на идее Беннера о повторяемости временных рядов для вершин и впадин, соответствует большинству разворотных точек фондового рынка этого столетия. Всегда ли будет данная модель отражать будущие максимумы – это другой вопрос. Помимо всего прочего, это фиксированные циклы, а не волны Эллиотта. Как бы то ни было, в наших поисках причины согласованности теории Беннера с реальностью мы обнаружили, что она достаточно точно сообразуется с последовательностью Фибоначчи в том, что повторяющиеся серии 8–9–10 дают числа Фибоначчи вплоть до 377, допуская погрешность в один пункт, что и показано ниже.

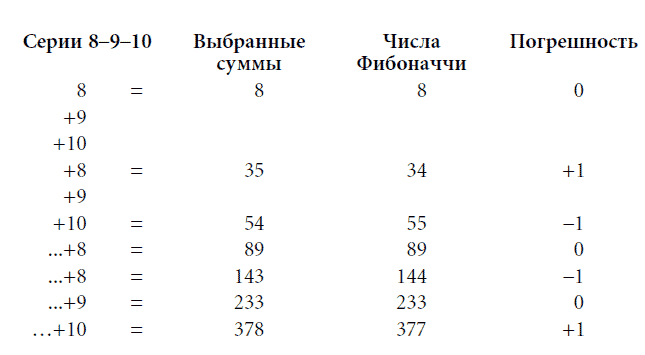
Наш вывод состоит в том, что теория Беннера, скорее основывающаяся на различных меняющихся временных периодах, чем на постоянно повторяющейся периодичности, соответствует структуре последовательности Фибоначчи. Если бы у нас не было опыта работы с методом Беннера, возможно, мы бы этого не заметили, но он доказал свою полезность в прошлом, когда применялся в сочетании с волновым анализом Эллиотта. А. Дж. Фрост применил концепцию Беннера в конце 1964 г., когда сделал невероятное (в то время) предсказание, что цены акций обречены на боковое движение в течение следующих десяти лет, достигнув максимума в 1000 пунктов промышленного индекса Доу – Джонса и минимума в зоне между 500 и 600 пунктами в конце 1974 – начале 1975 г. Далее следует текст письма, отправленного в то время Фростом Гамильтону Болтону. Рис. 4-19 воспроизводит приложенный к письму и снабженный примечаниями график. Поскольку письмо датировано 10 декабря 1964 г., оно представляет собой еще одно долгосрочное предсказание, основывающееся на теории Эллиотта, которое приходится рассматривать как факт, а не как фантазию.

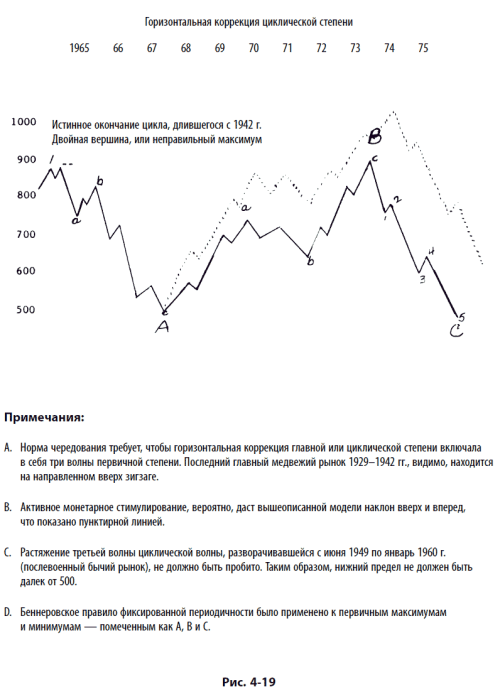
10 декабря 1964 года

Г-ну А. Г. Болтону Bolton, Tremblay & Co.

1245 Шербрук-Стрит

Западный Монреаль 25, Квебек

Дорогой Гамми!

Мы достаточно давно находимся в условиях экономической экспансии. Коррекция может начаться в любой момент. Поэтому имеет смысл достать с полки магический кристалл и произвести кое-какие вычисления. Я с огромным уважением отношусь к кредитной политике Вашего банка, за исключением моментов перелома важных трендов рынка. Я не могу забыть 1962 год. По моим ощущениям, все фундаментальные инструменты пригодны лишь в стабильной ситуации, причем их выводы, как правило, верны только в средне– и долгосрочной перспективе. Эллиотт, с другой стороны, хотя и труден в практическом применении, но обладает особенными достоинствами в момент разворотов рынка. По этой причине я обратил взор к волновому принципу, и то, что я сейчас вижу, меня весьма беспокоит. Насколько я могу судить исходя из Эллиотта, фондовый рынок находится на вершине, и конец главного цикла с 1942 года прямо перед нами.

…Я представлю свое доказательство того, что мы находимся в зоне опасности и что благоразумной инвестиционной политикой (если можно использовать это выражение в такой ситуации) было бы лететь в ближайшую брокерскую контору и избавляться от любых акций.

Третья волна, идущая с июня 1949 по январь 1960-го, является подволной долгого подъема, начавшегося в 1942 году, и представляет собой растяжение первичного цикла… затем весь цикл, начавшийся в 1942 году, возможно, достиг своей кульминационной истинной вершины. То, что теперь ждет нас впереди, возможно, является двойной вершиной и длинной горизонтальной коррекцией циклической степени.

…В соответствии с нормой чередования, следующие три первичных движения должны сформировать горизонтальную коррекцию значительной длительности. Интересно посмотреть, разовьется ли она. Тем временем я как последователь Эллиотта не боюсь делать прогноз на 10 лет, используя лишь идеи Эллиотта и Беннера. Ни один уважающий себя аналитик, кроме сторонников Эллиотта, не стал бы этого делать, но такой прогноз – именно то, на что вдохновляет эта уникальная теория.

С наилучшими пожеланиями,

А.Дж. Фрост.

Возможно, коэффициенты Фибоначчи проявляют себя на фондовом рынке и другими, неизвестными в настоящее время способами. Подходы, предложенные в данной главе, лишь призваны привлечь будущих аналитиков и указать им правильный путь. Рассмотрение анализа отношений в разрезе его сложности, точности и применимости продолжается и в следующих главах. Не вызывает сомнений, что анализ отношений – это мощный аналитический инструмент. Его совершенствование и расширение сферы его применимости – дело будущего.

Назад: Часть 2. Практическое использование теории Эллиотта

Дальше: Глава 5. Долгосрочные волны и их современное состояние