Мир одержим выстраиванием рейтингов. Мы составляем рейтинги атлетов, спортивных команд, больниц, ресторанов, фильмов, поп-музыки, студентов, коллег, городов, работы, машин, и т. д., и т. д. Нам нравится знать «самое-самое» – то, что входит в «первую десятку».

Это все чепуха, забавная чепуха, но тем не менее. Среди прочего чепуха происходит от того, насколько субъективна методология оценки. Если определенный ресторан в вашем городе признан лучшим, это не обязательно ваш любимый ресторан. Ваши предпочтения могут отличаться от суждений ресторанных критиков, а их взгляды на один и тот же вопрос зачастую прямо противоположны.

Можно выбрать объективную систему оценивания и все равно получать ничтожные результаты: например, оценивать фильмы по сумме выручки от их проката – это объективно и поддается подсчету. Можно аргументировано доказать: чем лучше фильм, тем больше людей жаждут заплатить за то, чтобы увидеть его. Но бывает такое, что фильм, сорвавший кассу, навевает на вас скуку, а малобюджетный инди-фильм западает в душу. Выручка от проката обычно говорит скорее о маркетинге, а не качестве картины.

Но, предположим, мы преодолели субъективность и достигли всеобщего соглашения относительно того, как сравнивать конкурентов. Попробуем выпарить идею ранжирования до ее математической сути. Улетучится ли тогда вся чепуха?

Сыграем в простую игру. Каждый бросит кубик, и у кого выпадет больше очков, тот выиграет. Если мы возьмем два обыкновенных кубика, где грани пронумерованы от одного до шести, то нет смысла говорить, что одна чем-то лучше другой. Они одинаковые.

Теперь сменим числа на гранях. Назовем наши игральные кости A и B.

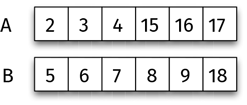
Какая из них лучше, A или B? Какую вы предпочтете?

Для того чтобы ответить на этот вопрос, рассмотрим все вероятности: как могут выпасть игральные кости? Если игральная кость A выпала числом 2 вверх, то для сравнения есть шесть вариантов того, как может выпасть игральная кость B. Если выпало число 3, вариантов для сравнения опять-таки шесть. Таким образом, есть 6 + 6 + 6 + 6 + 6 + 6 = 6 × 6 = 36 возможностей, и все они равновероятны. Иногда побеждает обладатель игральной кости A, иногда – обладатель игральной кости B (все числа на гранях разные, поэтому нет варианта сыграть раунд вничью). Кто выигрывает чаще?

Составим схему, включающую все 36 возможных комбинаций, где отмечено, кто выигрывает в каждом отдельном случае, A или B.

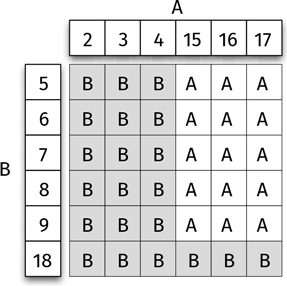
Становится очевидно, что игральная кость B лучше. В борьбе один на один B одолевает A чаще, чем наоборот. На схеме видно, что A побеждает в 15 случаях из 36, в то время как B – в 21 случае из 36.

Профессиональные игроки скажут, что шансы на победу A равны 15 против 21, а шансы на победу B равны 21 против 15. Вероятность того, что выиграет A, равна 15/36 (или 42 %), вероятность того, что выиграет B, равна 21/36 (или 58 %).

Как ни назови это преимущество, но B явно лучше A.

Добавим еще одну игральную кость. Внимание, появился новый соперник! Пусть на грани C нанесены числа, указанные на схеме.

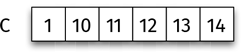
C рьяно вызывает на бой B. Кости кидают, и побеждает та, где выпало наибольшее число. Какая из них лучше, B или C? Как и раньше, начертим схему и посмотрим, какая игральная кость имеет больше шансов на победу.

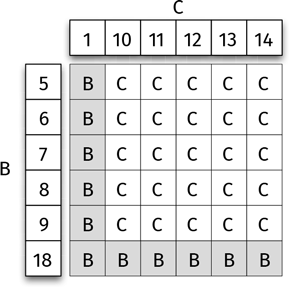
Мы видим, что C выигрывает гораздо чаще, чем B. Вероятность победы C равна 25/36 (около 69 %), в то время как B побеждает с вероятностью 11/36 (около 31 %).

В схватке один на один C лучше B, а B лучше A.

Значит, C лучше всех, верно?

Казалось бы, среди трех игральных костей A слабее всех, а C сильнее всех. Что будет, если C сразится с A? Разумеется, C победит?

Начертим снова схему всех возможностей:

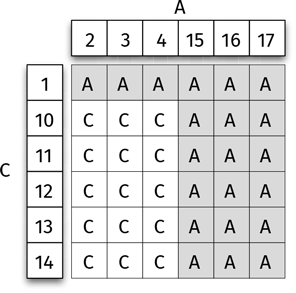
Посмотрите! A лучше C. Игральная кость A выигрывает с вероятностью 21/36 (около 58 %), а C – с вероятностью 15/36 (около 42 %).

Мы пришли к трем ошарашивающим выводам:

– B лучше A;

– C лучше B;

– A лучше C.

Ни одну из игральных костей нельзя назвать «лучшей», и ранжировать их бессмысленно.

Сколько еще рейтингов в нашей жизни лишены смысла?

Вот еще несколько игральных костей для изучения; эту задачу придумал Брэдли Эфрон, профессор статистики в Стэнфорде.

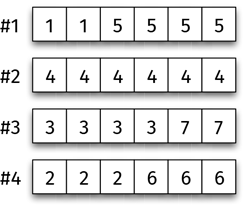
Сравним четыре игральные кости. Проработайте варианты, когда № 1 противостоит № 2, № 2 противостоит № 3, № 3 противостоит № 4, и № 4 противостоит № 1. Какая игральная кость лучше в каждой схватке? Как вы их проранжируете?

Ответы – в конце главы.

Вы играете в покер? Говоря точнее, вы играете в техасский холдем? Допустим, два человека играют в техасский холдем, и вы украдкой заглянули в их «карманные» карты. Пусть у первого на руках A♠K♥, а у второго 10♦9♦. У кого выше вероятность выиграть? У первого игрока карты большего достоинства, зато у второго игрока больше шансов на стрит и флэш.

Нам необходима дополнительная информация о пяти общих картах, лежащих рубашкой вниз. В колоде осталось 48 карт из 52. Нам придется перебрать все варианты, какими могут быть перетасованы эти карты, чтобы выяснить, какие пять карт окажутся на столе и кто из двух игроков победит (или же оба сыграют вничью). Есть около двух миллионов комбинаций по 5 карт из 48 карт. Нам не под силу провести все расчеты самостоятельно, поэтому прибегнем к помощи компьютера. Забейте в поисковик словосочетание «покерный калькулятор», и вы найдете уйму сайтов, где можно провести необходимые вычисления.

С помощью покерного калькулятора мы выясним, что игрок с «карманными» картами A♠K♥ побеждает с вероятностью 58,6 %, игрок с «карманными» картами 10♦9♦ побеждает в 41 % случаев, а 0,4 % остается на ничью.

Вывод: лучше иметь «карманные» карты A♠K♥, чем 10♦9♦.

Теперь ваша очередь. С помощью покерного калькулятора сравните шансы на выигрыш двух игроков со следующими наборами «карманных» карт:

– 10♦9♦ и 2♣2♥.

– 2♣2♥ и A♠K♥.

Дальше попробуйте построить рейтинг трех наборов «карманных» карт: A♠K♥, 10♦9♦ и 2♣2♥. Глава подошла к концу, поэтому вы вот-вот узнаете ответ.