Эта небольшая книга родилась из цикла публичных лекций, прочитанных физиком-теоретиком перед аудиторией из четырехсот человек, которая не сократилась даже после изначального предупреждения о сложности предмета и о том, что лекции нельзя назвать популярными, хотя в них практически не используется самое ужасное оружие физика, математическая дедукция, – не потому, что данный предмет можно объяснить без привлечения математики, а просто он слишком запутан для полного математического описания. Другой особенностью, которая придавала лекциям некий популярный оттенок, было намерение лектора объяснить и биологам, и физикам фундаментальную идею, лежащую на стыке биологии и физики.

В действительности, несмотря на разнообразие затрагиваемых тем, затея призвана донести лишь одну мысль – маленький комментарий к большому и важному вопросу. Чтобы не заблудиться, составим короткий план.

Большой, важный и весьма обсуждаемый вопрос заключается в следующем:

Как физика и химия объясняют события в пространстве и времени, происходящие в пространственных рамках живого организма?

Предварительный ответ, который попытается установить и обосновать эта книга, можно кратко изложить так:

Очевидная неспособность современных физики и химии объяснить подобные явления вовсе не означает, что эти науки не могут их объяснить.

Данное замечание было бы весьма тривиальным, если бы единственным его предназначением являлось пробудить надежду на достижение в будущем того, чего не удалось получить в прошлом. Однако его значение намного более оптимистично: эта неспособность имеет подробное объяснение.

Сегодня, благодаря блестящей работе биологов, в основном генетиков, за последние тридцать-сорок лет, мы знаем достаточно о действительной материальной структуре организмов и об их работе, чтобы заявить и назвать точную тому причину: современные физика и химия не могут объяснить пространственно-временные события, происходящие в живом организме.

Взаимодействия атомов в жизненно важных частях организма фундаментальным образом отличаются от всех соединений атомов, которые до настоящего времени являлись объектом экспериментальных и теоретических исследований физиков и химиков. Однако это различие, которое я считаю фундаментальным, может показаться малозначимым любому, кроме физика, сознающего, что законы химии и физики – сугубо статистические. Ведь именно со статистической точки зрения структура жизненно важных частей живых организмов столь отличается от любого кусочка материи, с которым мы, физики и химики, работаем физически в лабораториях или мысленно – за письменным столом. Невозможно представить, что законы и закономерности, открытые подобным образом, могут непосредственно применяться к поведению систем, не обладающих структурой, на которой они основаны.

Не-физик вряд ли окажется способен хотя бы уловить – не говоря уже о том, чтобы оценить – различие в «статистической структуре», выраженное столь абстрактными терминами. Чтобы придать утверждению живость и цвет, позвольте мне упомянуть то, что позднее будет описано намного детальнее, а именно самую значимую составляющую живой клетки – хромосомную фибриллу, которую можно назвать апериодическим кристаллом. До настоящего времени в физике мы имели дело лишь с периодическими кристаллами. В сознании скромного физика это очень интересные и сложные объекты, они относятся к самым удивительным и хитроумным материальным структурам, которыми озадачила его неживая природа. Однако в сравнении с апериодическими кристаллами они незамысловаты и скучны. Различия в структурах можно сравнить с различием между обычными обоями, на которых один и тот же узор повторяется снова и снова с регулярной периодичностью, и искусной вышивкой, например гобеленом Рафаэля, где нет скучного повторения, а присутствует сложный, гармоничный, осмысленный рисунок, созданный великим мастером.

Называя периодические кристаллы одним из самых сложных объектов исследования, я имел в виду истинного физика. Органическая химия, исследуя все более замысловатые молекулы, намного ближе подобралась к тому «апериодическому кристаллу», который, на мой взгляд, является материальным носителем жизни. Неудивительно, что химики-органики уже внесли важный вклад в проблему жизни, в то время как физики не сделали почти ничего.

Теперь, обозначив вкратце главную идею, а точнее, пределы наших исследований, я опишу линию атаки. Я предлагаю вначале рассмотреть представления наивного физика об организмах – то есть идеи, что могут возникнуть в сознании физика, который, выучив свою физику, а точнее, статистическое основание науки, начинает размышлять о них и о том, как они себя ведут и функционируют, и в конце концов честно спрашивает себя, способен ли он посредством того, чему научился, с точки зрения своей относительно простой, четкой и скромной науки, внести какой-либо существенный вклад в данную проблему.

Оказывается, вполне способен. Далее нужно сравнить его теоретические ожидания с биологическими фактами. Выяснится, что, хотя в целом его идеи представляются весьма разумными, они нуждаются в значительной коррекции. Таким образом мы постепенно приблизимся к правильной точке зрения – точнее, если выразиться более скромно, точке зрения, которую я считаю правильной.

Я не уверен, что мой подход является самым лучшим и простым. Однако он мой. Я сам был «наивным физиком». И не смог отыскать более простого и ясного пути к цели, нежели моя кривая дорожка.

Хороший способ развить представления наивного физика – начать со странного, почти нелепого вопроса: почему атомы такие маленькие? Да, они действительно очень малы. Каждый фрагмент материи, с которым мы имеем дело в повседневной жизни, состоит из множества атомов. Чтобы донести этот факт до аудитории, подобраны многочисленные примеры, самый впечатляющий из которых принадлежит лорду Кельвину. Представьте, что вы можете пометить молекулы в стакане воды; затем вылейте содержимое стакана в океан и тщательно перемешайте, чтобы равномерно распределить помеченные молекулы по семи морям. Если впоследствии вы наберете стакан воды в любом месте океана, то обнаружите в нем около сотни ваших меченых молекул. Разумеется, их будет не ровно 100 (даже если вычисления дают именно такой результат). Их будет 88, или 95, или 107, или 112, но вряд ли 50 или 150. Ожидаемое «отклонение», или «флуктуация», составит порядка корня квадратного из 100, то есть 10. Статистик выразит это так: вы обнаружите 100±10 молекул. Пока этот комментарий можно проигнорировать, однако позднее мы используем его в качестве иллюстрации статистического закона √n.

Реальный размер атомов составляет примерно длину волны желтого света. Это сравнение существенно, поскольку длина волны грубо характеризует размеры мельчайшего объекта, видимого в микроскоп. Таким образом, подобный объект содержит тысячи миллионов атомов. Но почему атомы такие маленькие? Очевидно, данный вопрос является уловкой, поскольку в действительности он касается вовсе не размера атомов, а размера организмов, точнее, наших собственных тел. Атом мал в сравнении с «гражданской» единицей длины, например, ярдом или метром. В атомной физике обычно используют так называемый ангстрем (сокращенно Å), который составляет 10^–10 метра, или, в десятичном представлении, 0,0000000001 метра. Диаметры атомов варьируют от 1 до 2 Å. «Гражданские» единицы, по сравнению с которыми атомы столь малы, тесно связаны с размерами наших тел. Согласно легенде, ярдом мы обязаны английскому королю-шутнику, которого советники спросили, какую единицу использовать. Он вытянул руку вбок и ответил: «Используйте расстояние от середины моей груди до кончиков пальцев, это подойдет». Правдива история или нет, но она важна для наших целей. Разумеется, король указал длину, сравнимую с его собственным телом, понимая, что любая другая будет неудобной. Несмотря на любовь к ангстремам, физик предпочитает слышать, что на его новый костюм потребуется шесть с половиной ярдов твида, а не шестьдесят пять тысяч миллионов ангстремов.

Таким образом, мы установили, что наш вопрос касается соотношения двух размеров – размера нашего тела и размера атома. С учетом неоспоримого главенства независимого существования атома, этот вопрос следует переформулировать так: почему наши тела столь велики в сравнении с атомом?

Представляю, как многие смышленые студенты-физики или химики оплакивали факт, что все наши органы чувств, составляющие вполне значимую часть организма, а следовательно с точки зрения вышеупомянутого соотношения состоящие из множества атомов, слишком грубы, чтобы ощутить влияние одиночного атома. Мы не можем увидеть, или почувствовать, или услышать отдельные атомы. Наши гипотезы на их счет заметно отличаются от непосредственных открытий, совершенных при помощи крупных органов чувств, и не могут быть проверены напрямую.

Обязательно ли это? Есть ли тому внутренняя причина? Можем ли мы проследить это состояние дел к некому первичному принципу, чтобы подтвердить и понять, почему ничто другое не совместимо с законами природы?

Наконец перед нами проблема, которую способен решить физик. Ответ на все эти вопросы утвердительный.

Если бы это было не так, если бы мы представляли собой организмы столь чувствительные, что один или несколько атомов сумели бы произвести ощутимое впечатление на наши чувства, – боже, какой была бы жизнь! Подчеркну: у подобного организма наверняка не развилось бы упорядоченное мышление, которое, пройдя немало ранних стадий, в конце концов сформировало бы, среди многих других идей, представление об атоме.

Мы выбираем именно этот момент, однако последующие рассуждения также применимы к работе других органов, а не только головного мозга и системы органов чувств. Тем не менее единственной действительно интересующей нас в нас самих вещью является то, что мы ощущаем, думаем и воспринимаем. По сравнению с физиологическим процессом, ответственным за мышление и чувства, остальные играют второстепенную роль, по крайней мере с точки зрения человека, если и не чисто объективной биологии. Более того, наша задача станет легче, если мы выберем для исследования процесс, тесно связанный с субъективными событиями, пусть и не осознавая истинной природы этого параллелизма. С моей точки зрения, он лежит за пределами естественных наук – и, вероятно, человеческого понимания.

Таким образом, перед нами возникает следующий вопрос: почему орган вроде нашего головного мозга, а также связанная с ним система органов чувств, должен состоять из невероятного числа атома, чтобы его физически изменчивое состояние соотносилось с высокоразвитым мышлением? Почему вышеупомянутая задача делает данный орган не совместимым с тем, чтобы являться – в целом или посредством периферических отделов, которые напрямую взаимодействуют с окружающей средой – инструментом достаточно тонким и чувствительным, чтобы зарегистрировать отдельный атом извне и отреагировать на него?

Причина такова: то, что мы называем мыслью, (1) само по себе упорядочено и (2) может использоваться лишь применительно к материалу, то есть восприятию или переживанию, обладающему определенным уровнем упорядоченности. Из этого вытекают два вывода. Во-первых, чтобы соотноситься с мышлением (как мой мозг соотносится с моей мыслью), физическая организация должна быть крайне упорядоченной, и это означает, что происходящие в ней события должны с высокой точностью подчиняться строгим физическим законам. Во-вторых, физические впечатления, которые производят на эту физически организованную систему внешние тела, очевидно, соотносятся с восприятием и опытом соответствующей мысли, формируя ее материал, как я выразился. Физические взаимодействия нашей системы с другими должны, как правило, сами обладать определенной степенью физической упорядоченности, то есть с определенной точностью подчиняться строгим физическим законам.

Почему же все это недостижимо для организма, состоящего из ограниченного числа атомов и способного ощутить воздействие одного или нескольких атомов?

Потому что мы знаем, что атомы постоянно находятся в неупорядоченном тепловом движении, которое, так сказать, противоречит упорядоченному поведению и не дает событиям, реализуемым небольшим числом атомов, соответствовать известным законам. Лишь в случае соединения невероятно большого числа атомов начинают действовать статистические законы, и они контролируют поведение этих скоплений с точностью, возрастающей вместе с ростом числа атомов. Именно таким образом события приобретают черты настоящей упорядоченности. Все физические и химические законы, играющие важную роль в жизни организмов, являются статистическими. Любой другой вид закономерности и упорядоченности нарушается и сводится на нет непрерывным тепловым движением атомов.

Позвольте проиллюстрировать это несколькими примерами, выбранными наугад из тысяч им подобных и потому, возможно, не самыми лучшими для читателя, который впервые слышит о таком положении вещей, – положении, столь же фундаментальном в современной физике и химии, как, например, клеточное строение организмов в биологии, или закон Ньютона в астрономии, или даже последовательность целых чисел – 1, 2, 3, 4, 5… – в математике. Следующие страницы вряд ли помогут новичку полностью понять и оценить предмет обсуждения, который связан с блистательными именами Уилларда Гиббса и Людвига Больцмана и обсуждается в учебниках в разделе «статистическая термодинамика».

Если заполнить вытянутую кварцевую трубку газообразным кислородом и поместить в магнитное поле, газ намагнитится. Я выбрал газ, поскольку случай с ним проще, чем с твердым веществом или жидкостью. Тот факт, что намагничивание в данном случае будет крайне слабым, не повлияет на теоретические рассуждения. Намагничивание происходит потому, что молекулы кислорода представляют собой маленькие магниты и ориентируются параллельно полю, как стрелка компаса. Но не думайте, будто они все выстраиваются параллельно. Удвоив силу поля, вы получите в вашем сосуде с кислородом двойную намагниченность, и она будет пропорционально возрастать по мере приближения к экстремально сильным полям.

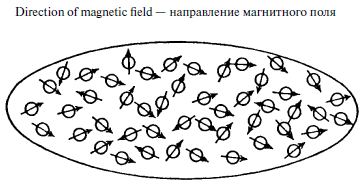
Рис. 1. Парамагнетизм

Это наглядный пример чисто статистического закона. Ориентации, вызванной полем, постоянно противостоит тепловое движение, приводящее к произвольной ориентации. Результатом этой борьбы является незначительное преобладание острых углов между осью диполя и полем над тупыми углами. Ориентация отдельных атомов непрерывно меняется, однако в среднем, благодаря своему огромному количеству, они дают постоянное небольшое преобладание ориентации в направлении поля, пропорциональное этому полю. Этим блистательным объяснением мы обязаны французскому физику П. Ланжевену. Проверить его можно следующим образом. Если наблюдаемая слабая намагниченность действительно является результатом противоборствующих явлений, а именно магнитного поля, желающего выстроить все молекулы параллельно, и теплового движения, которое стремится к произвольной ориентации, значит, можно усилить намагниченность, не повысив магнитное поле, а ослабив тепловое движение, то есть понизив температуру. Это подтверждает эксперимент, согласно ему намагниченность обратно пропорциональна абсолютной температуре, в количественном согласии с теорией (закон Кюри). Современное оборудование даже позволяет нам посредством понижения температуры настолько ослабить тепловое движение, что ориентирующее воздействие магнитного поля получит возможность если не проявить себя полностью, то достигнуть существенной доли «полной намагниченности». В данном случае мы уже не ждем, что удвоение силы поля удвоит намагниченность; последняя будет расти все меньше и меньше, приближаясь к так называемому насыщению. Это тоже подтверждает эксперимент.

Обратите внимание, что данное поведение полностью зависит от большого числа молекул, которые взаимодействуют, давая наблюдаемую намагниченность. В противном случае последняя не была бы постоянной, а весьма произвольно флуктуировала бы от секунды к секунде, свидетельствуя о переменных успехах в борьбе теплового движения и магнитного поля.

Заполнив нижнюю часть закрытого стеклянного сосуда туманом, состоящим из крошечных капель, вы увидите, что верхняя граница тумана будет постепенно опускаться с определенной скоростью, определяемой вязкостью воздуха и размером и удельной плотностью капель. Но изучив одну из капель под микроскопом, обнаружите, что она вовсе не опускается с постоянной скоростью, а совершает очень сложное движение, так называемое броуновское движение, которое лишь в среднем соотносится с общим оседанием.

Конечно, эти капли – не атомы, однако они достаточно малы и легки, чтобы ощутить влияние отдельных молекул, непрерывно бомбардирующих их поверхность. Поэтому капли отклоняются то в одну, то в другую сторону и лишь в среднем подчиняются действию силы тяжести.

Рис. 2. Оседающий туман

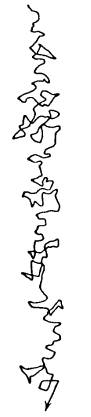
Рис. 3. Броуновское движение оседающей капли

Данный пример демонстрирует, какие забавные и хаотичные ощущения мы испытывали бы, если бы наши органы чувств воспринимали воздействие отдельных молекул. Существуют бактерии и другие организмы, которые столь малы, что на них этот феномен оказывает значительное влияние. Их движения определяются тепловыми капризами окружающей среды, у них просто нет выбора. Те из них, что обладают собственной способностью к перемещению, могут перебираться с места на место, однако с трудностями, поскольку тепловое движение швыряет их, словно утлую лодочку в бурном море.

На броуновское движение очень похоже явление диффузии. Представьте сосуд, заполненный водой, в которой растворено небольшое количество некоего окрашенного вещества, например перманганата калия, не в одинаковой концентрации, а как изображено на рис. 4, где точки обозначают молекулы растворенного вещества (перманганата) и концентрация падает слева направо. Если оставить этот сосуд в покое, начнется медленный процесс «диффузии», переносящий перманганат из левой части сосуда в правую, то есть из места с большей концентрацией в место с меньшей, пока вещество не распределится в воде равномерно.

Удивительной особенностью этого весьма простого и не слишком интересного процесса является то, что в его основе лежит не какая-то тенденция или сила, уводящая молекулы перманганата из более населенной области в менее населенную, словно жителей страны, переезжающих в свободные регионы. С нашими молекулами перманганата не происходит ничего подобного. Каждая ведет себя независимо от других, с которыми очень редко сталкивается. Каждая – как в населенной области, так и в пустой – постоянно испытывает удары молекул воды и постепенно движется в непредсказуемом направлении – иногда в область с большей концентрацией, порой в область с меньшей или вообще вбок. Перемещения такой молекулы часто сравнивают с движением на открытом пространстве слепого человека. Он одержим желанием «шагать», но не может выбрать направления, а потому непрерывно меняет свой курс.

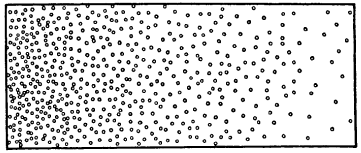
Рис. 4. Диффузия слева направо в растворе с различной концентрацией

То, что это случайное блуждание всех без исключения молекул перманганата должно привести к регулярному потоку в направлении меньшей концентрации и – в конце концов – к равномерному распределению, на первый взгляд вызывает недоумение. Если поделить рис. 4 на тонкие срезы с приблизительно постоянной концентрацией, молекулы перманганата, содержащиеся в данном конкретном срезе в некий момент времени, за счет случайного движения с равной вероятностью переместятся влево или вправо. Однако благодаря этому плоскость, разделяющую соседние срезы, пересечет больше молекул, приходящих слева, нежели справа, – просто потому, что слева находится больше молекул, вовлеченных в случайное движение. И пока это соответствует действительности, результатом будет регулярный поток слева направо – до достижения равномерного распределения.

Если перевести эти рассуждения на язык математики, закон диффузии будет представлять собой дифференциальное уравнение с частными производными:

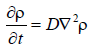
Я избавлю читателя от объяснений, хотя значение этого закона можно выразить простым языком. А именно: концентрация в любой конкретной точке возрастает или падает со временем пропорционально сравнительному избытку или недостатку концентрации в ее бесконечно малом окружении. Кстати, закон теплопроводности выглядит точно так же, только вместо концентрации стоит температура. Я привел этот суровый «математически строгий» закон, желая подчеркнуть, что его физическая точность должна, тем не менее, ставиться под сомнение в каждом конкретном случае. Он основан на случайности, и его правомерность приблизительна. Как правило, это очень хорошее приближение, но лишь благодаря огромному числу молекул, вовлеченных в явление. Чем меньше их количество, тем более сильных случайных отклонений следует ожидать – и они наблюдаются при неблагоприятных условиях.

Последний пример весьма похож на второй, однако представляет особый интерес. Легкое тело, подвешенное на длинной тонкой нити в равновесной ориентации, часто используется физиками для измерения слабых сил, которые отклоняют его от равновесия, электрических, магнитных или гравитационных сил, прикладываемых таким образом, чтобы повернуть тело вокруг вертикальной оси. Разумеется, выбор легкого тела должен соответствовать целям опыта. Непрерывные попытки повысить точность этих популярных «крутильных весов» выявили любопытный предел, интересный сам по себе. Если брать все более легкие тела и тонкие и длинные нити – чтобы равновесие было чувствительным к все более слабым силам, – предел достигается, как только подвешенное тело начинает ощущать влияние теплового движения молекул окружающей среды и исполнять непрерывный хаотический «танец» вокруг равновесного положения, подобно дрожащей капле. Подобное поведение не накладывает абсолютного предела на точность измерений, проведенных при помощи весов, однако подчеркивает практический предел. Неконтролируемое воздействие теплового движения конкурирует с воздействием измеряемой силы и делает отдельные наблюдаемые отклонения незначимыми. Следует провести множество измерений, чтобы исключить влияние броуновского движения на инструмент. Я считаю данный пример наиболее наглядным для нашего исследования, ведь наши органы чувств – тоже в определенном роде инструмент. Теперь мы видим, насколько бесполезными они станут, если обретут такую чувствительность.

Хочу добавить, что мог бы выбрать в качестве иллюстрации любой физический или химический закон из тех, что имеют значение для организма или его взаимодействий с окружающей средой. Подробное объяснение может оказаться более сложным, но суть будет той же, а потому описание станет монотонным.

Однако следует упомянуть одно важное численное утверждение относительно погрешности, которой следует ждать от любого физического закона, – правило √n. Вначале я проиллюстрирую его простым примером, а потом обобщу.

Если я предположу, что некий газ при определенных условиях – давлении и температуре – обладает определенной плотностью, и заявлю, что в определенном объеме (подходящем для какого-либо эксперимента) при этих условиях содержится n молекул газа, можете не сомневаться, что, проверив мое утверждение в некий момент времени, вы сочтете его ошибочным, с отклонением порядка √n. Соответственно, если n = 100, отклонение будет составлять около 10, а относительная ошибка – 10 %. Однако если n = 1 000 000, вы обнаружите отклонение около 1000, и относительная ошибка составит 0,1 %. Грубо говоря, данный статистический закон является весьма общим. 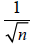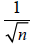Законы физики и физической химии неточны, и вероятная относительная ошибка для них составляет порядка , где n есть число молекул, которые взаимодействуют, чтобы данный закон работал – и был справедливым в пространственных или временных (либо пространственно-временных) рамках, значимых для каких-либо рассуждений или эксперимента.

Из этого снова следует, что для того чтобы получать выгоду от достаточно точных законов, как во внутренних процессах, так и во взаимодействии с внешним миром, организм должен обладать крупной структурой. Иначе число взаимодействующих частиц будет слишком маленьким, а «законы» – неточными. Особенно строгим требованием является корень квадратный. Хотя миллион – весьма большое число, точность 1000 к 1 не кажется слишком высокой, если правило претендует на звание «закона природы».