Глава 5. Алгоритмы

[Программирование является] привлекательным занятием не только потому, что оно перспективно с экономической и научной точек зрения, но и потому, что оно во многом может стать эстетическим опытом, как сочинение стихов или музыки.

Дональд Кнут

Человечество изыскивает решения все более и более трудных задач. В большинстве случаев вам приходится иметь дело с задачами, над примерными аналогами которых уже потрудились многие разработчики. Вполне вероятно, что они придумали эффективные алгоритмы, которые можно брать и использовать. Когда вы решаете задачи, вашим первым шагом всегда должен быть поиск существующих алгоритмов. В этой главе мы займемся исследованием хорошо известных алгоритмов, которые:

эффективно сортируют очень длинные списки;

быстро отыскивают нужный элемент;

оперируют и управляют графами;

используют исследование операций для оптимизации процессов.

Вы научитесь распознавать проблемы, к которым можно применить известные решения. Существует много различных типов задач: сор­тировка данных, поиск закономерностей (образов, шаблонов), прокладывание маршрута и др. И многие типы алгоритмов имеют непосредственное отношение к областям научно-практических исследований: обработке изображений, криптографии, искусственному интеллекту… В этой книге мы не сможем охватить их все. Однако мы изучим самые важные алгоритмы, с которыми должен быть знаком любой хороший программист.

5.1. Сортировка

До появления компьютеров сортировка данных была известной проблемой, ее ручное выполнение занимало колоссальное количество времени. Когда в 1890-х годах компания Tabulating Machine Company (которая позже стала называться IBM) автоматизировала операции сортировки, это позволило на несколько лет быстрее обработать данные переписи населения США.

Существует много алгоритмов сортировки. Более простые имеют временную сложность O(n2). Сортировка выбором (см. раздел «Оценка затрат времени» главы 2) — один из таких алгоритмов. Именно его люди предпочитают использовать для сортировки физической колоды карт. Сортировка выбором принадлежит многочисленной группе алгоритмов с квадратичной стоимостью. Мы, как правило, используем их для упорядочивания наборов данных, состоящих меньше чем из 1000 элементов. Одним из известных алгоритмов является сор­тировка вставками. Он показывает очень хорошую эффективность в сортировке уже почти упорядоченных наборов данных даже очень большого объема:

function insertion_sort(list)

    for i ← 2 … list.length

        j ← i

        while j and list[j-1] > list[j]

            list.swap_items(j, j-1)

            j ← j - 1

Выполните этот алгоритм на бумаге, с использованием большей частью отсортированного списка чисел. Для массивов, где не упорядочено незначительное число элементов, insertion_sort имеет сложность O(n). В этом случае он выполняет меньше операций, чем какой-либо другой алгоритм сортировки.

В отношении крупных наборов данных, о которых нельзя сказать, что они отсортированы большей частью, алгоритмы с временной сложностью O(n2) оказываются слишком медленными (см. табл. 3.2). Здесь нам нужны более эффективные подходы. Самыми известными высокоскоростными алгоритмами сортировки являются сортировка слиянием (см. раздел «Разделяй и властвуй» главы 3) и так называемая быстрая сортировка, оба имеют сложность O(n log n). Вот как алгоритм быстрой сортировки раскладывает по порядку колоду карт.

1. Если в колоде менее четырех карт, то упорядочить их — и работа завершена. В противном случае перейти к шагу 2.

2. Вынуть из колоды наугад любую карту, которая становится опорной.

3. Карты со значением больше, чем у опорной, кладутся в новую колоду справа; карты с меньшим значением кладутся в новую колоду слева.

4. Проделать эту процедуру для каждой из двух только что созданных колод.

5. Объединить левую колоду, опорную карту и правую колоду, чтобы получить отсортированную колоду (рис. 5.1).

 

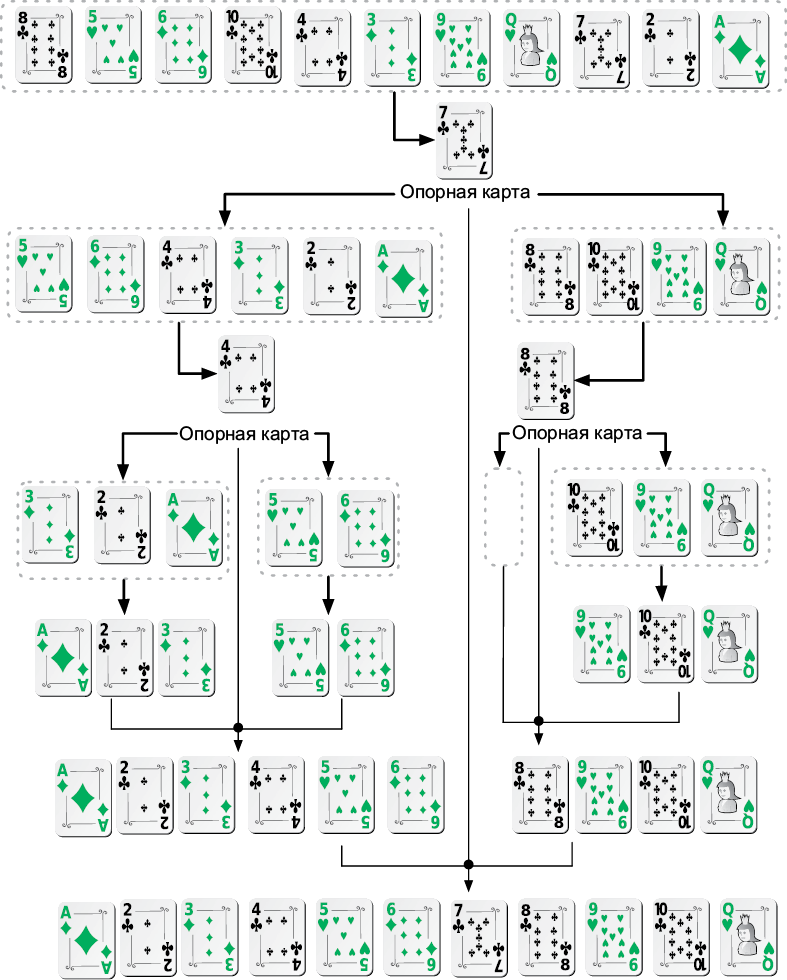
Рис. 5.1. Пример выполнения быстрой сортировки

Перетасуйте колоду карт и проделайте описанные шаги. Это поможет вам опробовать на практике алгоритм быстрой сортировки, а заодно укрепит ваше понимание рекурсии.

Теперь вы готовы решать большинство задач, связанных с сортировкой. Здесь мы осветили не все алгоритмы сортировки, так что просто помните, что их гораздо больше и каждый из них соответствует конкретным задачам.

5.2. Поиск

Поиск определенной информации в памяти является ключевой операцией в вычислениях. Программисту очень важно владеть алгоритмами поиска. Самый простой из них — последовательный поиск: вы просматриваете все элементы один за другим, пока не будет найден нужный; как вариант, вы можете проверить все элементы, чтобы понять, что искомого среди них нет.

Легко заметить, что последовательный поиск имеет сложность O(n), где n — это общее количество элементов в пространстве поиска. Но на случай, когда элементы хорошо структурированы, есть более эффективные алгоритмы. В разделе «Структуры» предыдущей главы мы убедились, что извлечение данных, представленных в формате сбалансированного двоичного дерева поиска, стоит всего O(log n).

Если ваши элементы хранятся в сортированном массиве, то их можно отыскать за такое же время, O(log n), посредством двоичного поиска. Этот алгоритм на каждом шаге отбрасывает половину пространства поиска:

function binary_search(items, key)

    if not items

        return NULL

    i ← items.length / 2

    if key = items[i]

        return items[i]

    if key > items[i]

        sliced ← items.slice(i+1, items.length)

    else

        sliced ← items.slice(0, i-1)

    return binary_search(sliced, key)

На каждом шаге алгоритм binary_search выполняет постоянное число операций и отбрасывает половину входных данных. Это означает, что для n элементов пространство поиска сведется к нулю за log2n шагов. Поскольку на каждом шаге выполняется постоянное количество операций, алгоритм имеет сложность O(log n). Вы можете выполнять поиск среди миллиона или триллиона элементов, и этот алгоритм по-прежнему будет показывать хорошую производительность.

Впрочем, существуют еще более эффективные алгоритмы. Если элементы хранятся в хеш-таблице (см. раздел «Структуры» предыдущей главы), достаточно вычислить хеш-ключ искомого элемента. Этот хеш даст его адрес! Время, необходимое для нахождения элемента, не меняется с увеличением пространства поиска. Не имеет значения, ищете вы среди миллионов, миллиардов или триллионов элементов, — количество операций останется постоянным, а значит, процесс имеет временную сложность O(1), он действует почти мгновенно.

5.3. Графы

Мы уже знаем, что графы — гибкая структура данных, которая для хранения информации использует вершины и ребра. Графы широко используются для представления таких данных, как социальные сети (вершины — люди, ребра — дружеские связи), телефонные сети (вершины — телефоны и станции, ребра — линии связи) и многих других.

Поиск в графах

Как найти узел в графе? Если структура графа не предоставляет никакой помощи в навигации, вам придется посетить каждую вершину, пока не обнаружится нужная. Есть два способа сделать это: выполнить обход графа в глубину и в ширину (рис. 5.2).

 

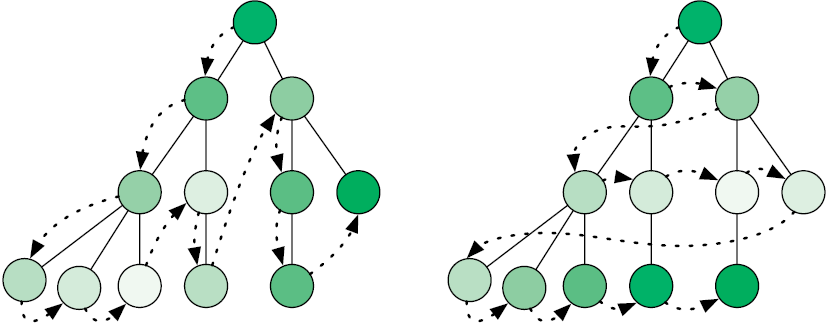
Рис. 5.2. Обход графа в глубину против обхода в ширину

Выполняя поиск в графе в глубину (DFS, depth first search), мы продвигаемся вдоль ребер, уходя все глубже и глубже в граф. Достигнув вершины без ребер, ведущих к каким-либо новым вершинам, мы возвращаемся к предыдущей и продолжаем процесс. Мы используем стек, чтобы запомнить путь обхода графа, помещая туда вершину на время ее исследования и удаляя ее, когда нужно вернуться. Стратегия поиска с возвратом (см. соответствующий раздел главы 3) выполняет обход решений точно так же.

function DFS(start_node, key)

    next_nodes ← Stack.new()

    seen_nodes ← Set.new()

 

    next_nodes.push(start_node)

    seen_nodes.add(start_node)

    while not next_nodes.empty

        node ← next_nodes.pop()

        if node.key = key

            return node

        for n in node.connected_nodes

            if not n in seen_nodes

                next_nodes.push(n)

                seen_nodes.add(n)

    return NULL

Если обход графа вглубь не кажется приемлемым решением, можно попробовать обход в ширину (BFS, breadth first search). В этом случае обход графа выполняется по уровням: сначала соседей начальной вершины, затем соседей его соседей и т.д. Вершины для посещения запоминаются в очереди. Исследуя вершину, мы ставим в очередь ее дочерние вершины, затем определяем следующую исследуемую вершину, извлекая ее из очереди.

function BFS(start_node, key)

    next_nodes ← Queue.new()

    seen_nodes ← Set.new()

 

    next_nodes.enqueue(start_node)

    seen_nodes.add(start_node)

 

    while not next_nodes.empty

        node ← next_nodes.dequeue()

        if node.key = key

            return node

        for n in node.connected_nodes

            if not n in seen_nodes

                next_nodes.enqueue(n)

                seen_nodes.add(n)

    return NULL

Обратите внимание, что алгоритмы DFS и BFS отличаются только способом хранения следующих исследуемых вершин: в одном случае это очередь, в другом — стек.

Итак, какой подход нам следует использовать? Алгоритм DFS более прост в реализации и использует меньше памяти: достаточно хра-

 

Рис. 5.3. Поиск в графе в глубину

нить родительские вершины, ведущие к текущей исследуемой вершине. В BFS придется хранить всю границу процесса поиска. Если граф состоит из миллиона вершин, это может оказаться непрак­тичным.

Когда есть основания предполагать, что искомая вершина не находится многими уровнями ниже начальной, обычно имеет смысл заплатить более высокую стоимость BFS, потому что так вы, скорее всего, закончите поиск быстрее. Если нужно исследовать абсолютно все вершины графа, лучше придерживаться алгоритма DFS из-за его простой реализации и меньшего объема потребляемой памяти.

Рис. 5.3 показывает, что выбор неправильного метода обхода может иметь страшные последствия.

Раскраска графов

Задачи раскраски графов возникают, когда есть фиксированное число «красок» (либо любой другой набор меток) и вы должны назначить «цвет» каждой вершине в графе. Вершины, которые соединены ребром, не могут иметь одинаковый «цвет». В качестве примера давайте рассмотрим следующую задачу.

Помехи Дана карта вышек сотовой связи и районов обслуживания. Вышки в смежных районах должны работать на разных частотах для предотвращения помех. Имеется четыре частоты на выбор. Какую частоту вы назначите каждой вышке?

Первый шаг состоит в моделировании задачи при помощи графа. Вышки являются вершинами в графе. Если две из них расположены настолько близко, что вызывают помехи, соединяем их ребром. Каждая частота имеет свой цвет.

Как назначить частоты приемлемым способом? Можно ли найти решение, которое использует всего три цвета? Или два? Определение минимально возможного количества цветов на самом деле является NP-полной задачей — для этого подходят только экспоненциальные алгоритмы.

Мы не покажем алгоритм для решения данной задачи. Используйте то, чему вы научились к настоящему моменту, и попробуйте решить задачу самостоятельно. Это можно сделать на сайте UVA с онлайн-экспертом, который протестирует предложенное вами решение, выполнит ваш программный код и сообщит, работоспособен ли он. Если с кодом окажется все в порядке, эксперт также оценит время выполнения вашего кода в сравнении с тем, что написали другие люди. Дерзайте! Продумайте алгоритмы и стратегии решения данной задачи и испытайте их. Чтение книги может лишь подвести вас к решению. Взаимодействие с онлайновым экспертом даст вам практический опыт, необходимый для того, чтобы стать отличным программистом.

Поиск путей в графе

Поиск кратчайшего пути между узлами является самой известной графовой задачей. Системы навигации GPS проводят поиск в графе улиц и перекрестков для вычисления маршрута. Некоторые из них даже используют данные дорожного движения с целью увеличения веса ребер, представляющих улицы, где образовался затор.

Для поиска кратчайшего пути вполне можно использовать стратегии BFS и DFS, но это плохая идея. Одним из хорошо известных и очень эффективных способов поиска кратчайшего пути является алгоритм Дейкстры. В отличие от BFS, для запоминания просматриваемых вершин алгоритм Дейкстры использует очередь с приоритетом. Когда исследуются новые вершины, их связи добавляются в эту очередь. Приоритетом вершины является вес ребер, которые приводят ее в стартовую вершину. Благодаря этому следующая исследуемая вершина всегда оказывается самой близкой к месту, откуда мы начали.

Известны случаи, когда алгоритм Дейкстры зацикливается, не в силах найти конечную вершину. Процесс поиска может быть обманут отрицательным циклом, который приводит к бесконечному исследованию вершин. Отрицательный цикл — это путь в графе, чье начало и конец приходятся на одну вершину с весом ребер на пути, в сумме дающим отрицательное значение. Если вы ищете кратчайший путь в графе, где ребра могут иметь отрицательный вес, будьте начеку.

А что, если граф, в котором вы ищете, огромен? Для ускорения можно использовать двунаправленный поиск. Два процесса поиска выполняются одновременно: один начинает со стартовой вершины, другой — с конечной. Когда оказывается, что вершина, обнаруженная в одном пространстве поиска, также присутствует в другом, это значит, что у нас есть путь. Пространство поиска в таком случае вдвое меньше, чем в однонаправленным поиске. Посмотрите на рис. 5.4: серое пространство меньше белой области.

 

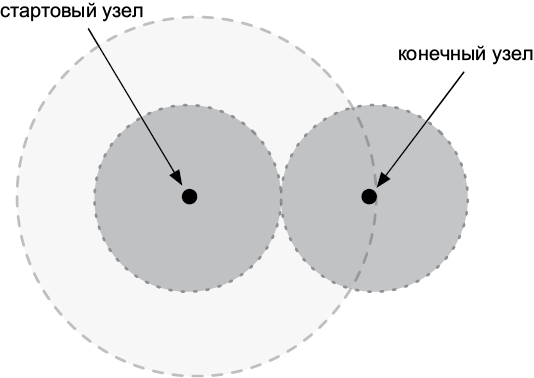
Рис. 5.4. Пространства однонаправленного и двунаправленного поиска

 

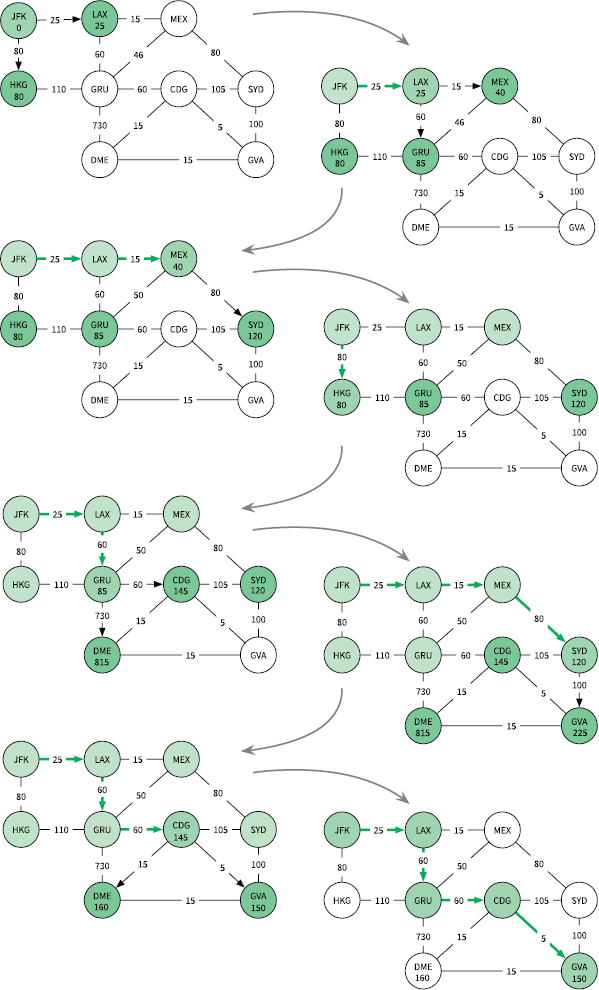
Рис. 5.5. Поиск кратчайшего маршрута от аэропорта JFK до аэропорта GVA при помощи алгоритма Дейкстры

PageRank

Вы когда-нибудь задавались вопросом, как поисковой системе Google удается анализировать миллиарды веб-страниц и показывать вам самые подходящие? В этом процессе задействовано множество алгоритмов, но самым важным является алгоритм PageRank.

Прежде чем основать компанию Google, Сергей Брин и Ларри Пейдж работали научными сотрудниками в области computer science в Стэнфордском университете и занимались исследованием графовых алгоритмов. Они смоделировали Всемирную паутину в виде графа: веб-страницы — это вершины, и связи между ними — ребра.

Они решили, что если веб-страница получает много связей от других важных страниц, то она тоже должна быть важной. Опираясь на эту идею, они создали алгоритм PageRank. Он выполняется в несколько заходов. Вначале каждая веб-страница в графе имеет то же количество единиц значимости, что и остальные. После каждого захода она распределяет свои единицы среди страниц, ссылки на которые на ней размещены. Этот процесс повторяется до тех пор, пока все значения не стабилизируются. Стабилизированная оценка каждой страницы называется ее рангом, отсюда и название — PageRank (англ. «ранг страницы»). Используя этот алгоритм для определения важности веб-страниц, поисковая система Google быстро заняла доминирующую позицию среди других аналогичных сервисов.

Алгоритм PageRank применим и к другим типам графов. Например, мы можем смоделировать пользователей сети Twitter на графе, а затем вычислить ранг каждого. Как вы считаете, будут ли пользователи с более высоким рангом известными людьми?

5.4. Исследование операций

Во время Второй мировой войны британская армия столкнулась с необходимостью оптимизировать принятие стратегических решений, чтобы повысить действенность операций. Было разработано большое количество аналитических инструментов для выявления наилучшего способа координации военных действий.

Эта практическая дисциплина получила название исследование операций. Она позволила усовершенствовать британскую систему радаров дальнего обнаружения и помогла Соединенному Королевству лучше управлять людскими и материальными ресурсами. Во время войны сотни британцев участвовали в исследовании операций. В дальнейшем для оптимизации процессов в торгово-промышленной деятельности были применены новые идеи. Исследование операций включает в себя определение целевого показателя, который подлежит оптимизации, то есть максимизации или минимизации. Эта дисциплина позволяет максимизировать такие целевые показатели, как урожай, прибыль или производительность, и минимизировать убытки, риск или стоимость.

Например, исследование операций используется авиакомпаниями для оптимизации графиков полетов. Точные корректировки в планировании распределения трудовых ресурсов и оборудования могут сэкономить миллионы долларов. Еще один пример касается нефтеперерабатывающих заводов, где определение оптимальных пропорций сырья в смеси может рассматриваться как задача исследования операций.

Задачи линейной оптимизации

Задачи, где целевой показатель и ограничения можно смоделировать с использованием линейных уравнений, называются задачами линейной оптимизации. Давайте посмотрим, как решаются эти задачи.

Умная меблировка В вашем офисе не хватает каталожных шкафов. Шкаф X стоит 10 долларов, занимает 6 квадратных футов и содержит 8 кубических футов папок. Шкаф Y стоит 20 долларов, занимает 8 квадратных футов и содержит 12 кубических футов папок. У вас есть 140 долларов, и вы можете использовать под шкафы до 72 квадратных футов площади офиса. Какие шкафы следует приобрести, чтобы максимизировать емкость хранения?

Прежде всего определим переменные нашей задачи. Мы хотим найти количество шкафов каждого типа, которые следует приобрести, поэтому:

• x — количество шкафов модели X;

• y — количество шкафов модели Y.

Мы хотим максимизировать емкость хранения. Дадим емкости хранения имя z и смоделируем это значение как функцию от x и y:

• z = 8x + 12y.

Теперь выберем значения x и y, которые дадут максимальное значение z. При этом мы должны соблюсти ограничение по бюджету (то есть уложиться в 140 долларов) и по площади (она должна быть меньше 72 квадратных футов). Смоделируем эти ограничения:

• 10x + 20y ≤ 140 (ограничение по бюджету);

• 6x + 8y ≤ 72 (ограничение по площади);

• x ≥ 0, y ≥ 0 (нельзя купить отрицательное количество шкафов).

Как бы вы решили эту задачу? Покупка максимального количества шкафов с наилучшим соотношением хранение/площадь не является правильным решением, потому что пространство под установку шкафов ограниченно. Можно пойти по пути полного перебора: написать программу, вычисляющую z для всех возможных x и y, и получить пару, дающую оптимальное z. Это решение годится для простых задач, но оно невыполнимо при большом количестве переменных.

Оказывается, что решать задачи линейной оптимизации вроде этой можно и без программирования. Нужно просто использовать правильный инструмент для работы: симплекс-метод. Он очень эффективно справляется с задачами линейной оптимизации. Симплекс-метод помогает целым отраслям решать сложные проблемы, начиная с 1960-х годов. Когда перед вами встанет такая задача, не изобретайте колесо, просто возьмите готовый симплексный решатель.

Симплексные решатели требуют указать функцию для максимизации (или минимизации) и уравнения, моделирующие ограничения. Решатель сделает все остальное. В данной задаче максимальное значение z достигается при x = 8 и y = 3.

 

Рис. 5.6. Значения x и y, удовлетворяющие ограничениям задачи

Симплекс-метод отыскивает оптимальное значение в пространстве приемлемых решений. Чтобы понять механику его работы, представим все возможные значения x и y на двумерной плоскости (рис. 5.6). Ограничения по бюджету и площади представлены на графике линиями.

Обратите внимание, что пространство всех возможных решений является замкнутой областью на графике. Доказано, что оптимальным решением линейной задачи должна быть угловая точка замкнутой области — та, где пересекаются линии, представляющие ограничения. Симплекс проверяет угловые точки и вычисляет, которая из них оптимизирует z. Отнюдь не просто визуализировать этот процесс в задачах линейной оптимизации, имеющих более двух переменных, но математический принцип везде работает одинаково.

Задачи о максимальном потоке в Сети

Многие задачи, касающиеся сетей и потоков, можно сформулировать с точки зрения линейных уравнений и, следовательно, решить при помощи симплекс-метода. Например, во время холодной войны армия США вычисляла маршруты пополнения материально-технических запасов, которые Советский Союз мог использовать в Восточной Европе (рис. 5.7).

 

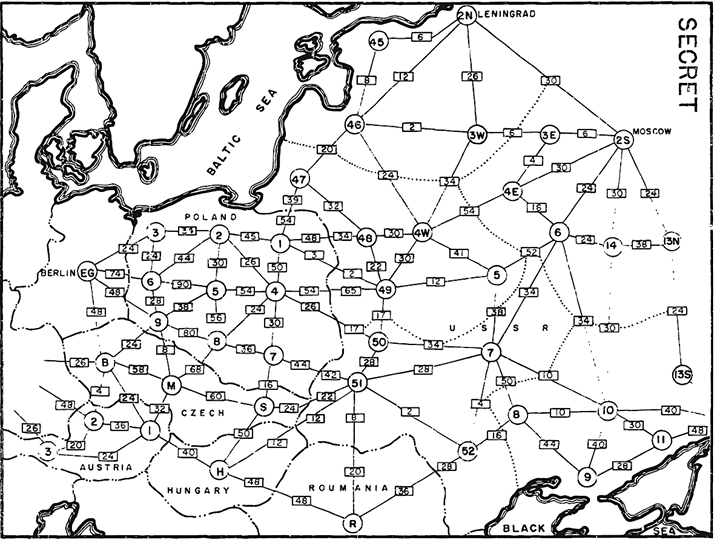
Рис. 5.7. Рассекреченный военный отчет 1955 г., показывающий пропускную способность советской сети железных дорог

Сеть снабжения Сеть железных дорог представлена линиями, которые соединяют города. Каждая имеет максимальную пропускную способность — самый большой ежедневный поток грузов. Какой объем можно перевезти из заданного производящего города в заданный потребляющий город?

Чтобы смоделировать задачу с линейными уравнениями, каждой железной дороге нужно назначить переменную, представляющую объем грузов, который она сможет перевезти. Ограничения следующие: ни одна железная дорога не может перевезти больше своей пропускной способности; входящий поток грузов должен быть эквивалентен исходящему во всех населенных пунктах, кроме производящего и потребляющего городов. Затем нужно подобрать такие значения для переменных, которые позволят доставить в получающий город максимум грузов.

Мы не будем подробно расписывать, как отобразить эту задачу в линейной форме. Наша цель здесь состоит только в том, чтобы донести мысль, что многие задачи оптимизации с привлечением графов, стоимости и потоков можно легко решить существующими реализациями симплекс-метода. В Сети есть вся необходимая документация. Смотрите в оба и не изобретайте колеса.

Подведем итоги

Мы показали несколько хорошо известных алгоритмов и методов решения самых разнообразных задач. Первым делом, приступая к решению новой задачи, всегда старайтесь найти готовый алгоритм или метод.

Существует большое количество важных алгоритмов, которые мы не смогли включить в эту главу. Например, имеются поисковые алгоритмы, более продвинутые, чем алгоритм Дейкстры (такие как, A*), алгоритмы, оценивающие подобие двух слов (расстояние редактирования Левенштейна), алгоритмы машинного обучения и многие другие…

Полезные материалы

• Комен Т., Лейзерсон Ч.И., Ривест Р.Л., Штайн К. Алгоритмы. Построение и анализ. — М.: «Вильямс», 2016.

• Алгоритмы (Algorithms, Sedgewick, см. ).

• Простая модель линейного программирования (Simple Linear Programming Model, Katie Pease, см. ).