Книга: Большой роман о математике. История мира через призму математики
Назад: 11 Воображаемые миры
Дальше: 13 Мировой алфавит
12
Язык математики

XVI в. в Европе был богат событиями. Ренессанс начался в Италии, а затем распространился по всему континенту. Сделаны многочисленные открытия. На западе, за Атлантическим океаном, испанские корабли открыли новый мир. И в то время как исследователи отправлялись на поиски далеких неизведанных земель, интеллектуалы-гуманитарии в библиотеках заново постигали великие тексты эпохи Античности. В религии также начали происходить изменения. Протестантская реформация во главе с Мартином Лютером и Жаном Кальвином набирала все большую популярность, и во второй половине века в Европе бушевали религиозные войны.
Быстрое распространение новых идей в значительной степени обязано изобретению печати подвижными литерами, разработанной в 1450 г. немецким ученым Иоганном Гутенбергом. Благодаря этому методу стало можно очень быстро перепечатывать книги, что обеспечивало их широкое распространение. В 1482 г. «Начала» Евклида стали первым математическим трудом, который напечатали в Венеции. Успех был огромный! В начале XVI в. в сотнях городов были свои печатные станки и напечатали уже десятки тысяч книг.
Наука играла активную роль в происходивших изменениях. В 1543 г. польский астроном Николай Коперник опубликовал свою работу «О вращении небесных сфер» (De Revolutionibus Orbium Coelestium). Эффект от нее был как гром среди ясного неба! Перечеркивая учение Птолемея, Коперник утверждал, что это Земля вращается вокруг Солнца, а не наоборот! В последующие годы Джордано Бруно, Иоганн Кеплер и Галилео Галилей подтвердили данное открытие и провозгласили гелиоцентрическую систему мира. Это революционное открытие вызвало гнев деятелей католической церкви. После длительного застоя наука начала стремительно развиваться, и многие догмы были опровергнуты. Если Копернику хватило благоразумия не публиковать свою работу вплоть до момента незадолго до своей смерти, то Бруно не был так сдержан, и вследствие этого его сожгли на костре на площади в Риме, а Галилео Галилея заставили отречься от своего учения перед судом инквизиции. Легенда гласит, что, выйдя из зала судебных заседаний, итальянский ученый пробормотал знаменитую фразу: «И все-таки она вертится!»
Математика продолжает постепенно распространяться по крупным государствам на западе. Так, она проникает и во Францию.
Разумеется, математикой здесь занимались и раньше. У галлов была своя система исчисления на основе двадцаток, в результате чего в современном французском языке 80 переводится дословно как «четыре по двадцать». Древние римляне, несмотря на отсутствие великих математиков, неплохо умели считать в целях обеспечения хозяйственной деятельности своей огромной империи. Эти знания унаследовали Франки, Меровинги, Каролинги и Капетинги в эпоху Средневековья. Тем не менее во Франции никогда не было великих математиков, а также не сделано значительных математических открытий или приведено доказательств каких-либо теорем, которые бы не были доказаны ранее.
Поскольку математика добралась до Франции, самое время пойти по ее следам здесь. Направимся в департамент Вандея, в западную часть страны, где жил первый великий французский математик Возрождения Франсуа Виет.
Деревня Фуссе-Пейре в двенадцати километрах от Фонтене-ле-Конт навсегда останется в истории. Первые следы поселений в этом месте относятся к галло-римским временам, но период его процветания наступит только в эпоху Ренессанса. Многочисленные ремесленники и торговцы приезжали сюда, и их дела шли прекрасно. О местных торговцах шерстью, льном и кожей знали во всем королевстве. Даже сегодня многие здания этого периода замечательно сохранились. В деревне с населением всего в тысячу человек осталось не менее четырех исторических зданий и множество других строений.
К северу от деревни расположено местечко под названием Ла-Биготье, бывшая ферма, которую Франсуа Виет унаследовал от своего отца и которой он обязан своей благородной фамилией де ля Биготье. На центральной улице расположена старая гостиница «Святая Екатерина», ранее принадлежавшая семье Виет, где математик любил проводить время в юности. Есть причина, по которой мне было так интересно попасть в то место, где вырос первый великий математик страны. Без сомнения, молодой Франсуа провел много зимних вечеров перед гигантским камином в центре главной комнаты, где сейчас находится столовая. Может быть, именно здесь, согретый жаром тлеющих угольков, он впервые начал задумываться о вопросах математики?
Виет не всю свою жизнь прожил в Фуссе-Пейре. Получив юридическое образование в Пуатье, он отправился в Лион, где был представлен королю Карлу IX, а затем пробыл некоторое время в Ла-Рошели, перед тем как окончательно обосновался в Париже.
Религиозные войны достигли к этому моменту своего апогея. Семья Франсуа разделилась из-за убеждений. Его отец, Этьенн Виет, перешел в протестантизм, а два его дяди остались католиками. Франсуа занимал нейтральную позицию по этому вопросу и никогда открыто не говорил о своих убеждениях. Он одновременно выступал на стороне как влиятельных протестантских семей, так и представителей правящей элиты. Такое его поведение вызывало периодическое недовольство, в результате чего он несколько раз оказывася в немилости. В Варфоломеевскую ночь в 1572 г. он был в Париже, но ему удалось выжить. Не все оказались так удачливы: Пьера де ла Раме, который был первым, кто стал преподавать математику в Парижском университете и чьи работы оказали сильное влияние на Виета, убили 26 августа.
Наряду со своими служебными обязанностями Виет в свободное от работы время занимался математикой. Он, разумеется, был знаком с работами Евклида, Архимеда и других античных ученых, исследования которых переосмыслили в эпоху Ренессанса. Также Виет интересовался работами итальянских ученых и стал одним из первых, кто прочитал «Алгебру» Бомбелли, публикация которой прошла довольно незаметно. Французский математик, однако, скептически относится к введению комплексных чисел. На протяжении всей жизни Виет печатал математические исследования за свой счет и предлагал прочитать их только тем, кто, по его мнению, этого заслуживал. Он интересовался вопросами астрономии, тригонометрии или криптографии.
В 1591 г. Виет опубликовал свою основную работу: «Введение в искусство анализа» (In artem analyticem isagoge), также известную как «Исагогика». Как ни странно, «Исагогика» посвящена не теоремам или математическим доказательствам, а непосредственно используемым в математике формулировкам. Виет был одним из основоположников новой алгебры, которая сформировалась в течение нескольких последующих десятилетий и стимулировала появление нового математического языка.
Для того чтобы лучше понять, о чем идет речь, необходимо вспомнить математические работы эпохи Античности. В то время как геометрические теоремы Евклида и алгебраические методы аль-Хорезми актуальны и по сей день, сама форма изложения коренным образом изменилась. У ученых эпохи Античности не было конкретного языка для описания математических действий. Все известные нам символы, которые используются для обозначения четырех основных операций, +, —, × и ÷, изобрели только в эпоху Ренессанса. На протяжении почти пяти тысячелетий математики Месопотамии, арабского мира, Древней Греции, Китая использовали в своих математических формулах записи на местных языках.
Так, книги аль-Хорезми и алгебраистов Багдада были полностью написаны на арабском языке без использования символов. Если в то время для описания действия было необходимо несколько страниц, то сейчас обходятся несколькими строками. Помните уравнение второй степени, описанное в книге «аль-джабр»:
Квадрат неизвестного числа плюс двадцать один равен числу, в десять раз больше неизвестного.
Аль-Хорезми описывал решение этого уравнения следующим образом.
Квадраты и числа равны корням; например, «сумма квадрата числа и двадцати одного равна десяти квадратным корням этого квадрата». То есть чему должен быть равен квадрат числа, для того чтобы в сумме с двадцатью одним дирхамом он был равен десяти корням квадрата этого числа? Решение: возьмем половину числа корней, т. е. пять. Умножим это число на себя – получим двадцать пять. Вычтем из получившегося результата двадцать один – остается четыре. Извлечем из результата корень – получится два. Вычтем два от половины корней, что составляет пять, – получается три. Это корень, квадрат которого равен девяти. Можно также прибавить корень к половине корней – сумма будет равна семи; это корень искомого квадрата, а его квадрат равен сорока девяти.
Этот текст в наше время покажется очень косноязычным даже студентам, которые изучают данный вопрос. Уравнение имеет два решения: 9 и 49.
Риторическая алгебра, как ее окрестили впоследствии, не только слишком громоздка в описании, но и неоднозначна с точки зрения формулировок, которые могут быть истолкованы различным образом. Учитывая сложность аргументации и доказательств, эта форма изложения становится крайне неудобной для использования.
К этим сложностям математики иногда добавляют дополнительные. Например, многие математические работы того времени написаны в стихах. Это явление зачастую было связано с тем, что математические факты заучивались наизусть, а в стихотворной форме это сделать проще. Когда Тарталья передал свой метод решения уравнений третьей степени Кардано, тот опубликовал его на итальянском и александрийском языках. Разумеется, доказательство, написанное в стихотворной форме, становится более сложным для восприятия, в связи с чем есть мнение, что Тарталья целенаправленно писал доказательство в такой форме, чтобы его было сложнее понять. Вот перевод отрывка его работы.
Если известно, что куб и значения
Равны по количеству между собой,
Возьмем еще два других, отличных от них.
Затем получаем, что
Их производная равна
Кубу трети значения.
Затем, вычислив
Их кубический корень,
Вы найдете значение.
Очень замысловато написано, не правда ли? Тарталья называет значением неизвестную, искомую величину. Присутствие слова «куб» в этом отрывке четко указывает на то, что речь идет о кубическом уравнении. Сам Кардано с трудом разобрал смысл содержания этого отрывка.
Чтобы упросить восприятие своих работ, математики постепенно начали упрощать алгебраический язык. Этот процесс начался в Западной части мусульманского мира в эпоху позднего Средневековья и особенно активно набрал обороты в Европе в период XV–XVI вв.
Впервые в истории в математике появились специальные слова. Так, уэльский математик Роберт Рекорд предложил в середине XVI в. термины для обозначения степеней неизвестных чисел, основанные на системе префиксов, которые могут добавляться до бесконечности. Квадрат неизвестного, например, назывался зензике (zenzike), шестая степень – зензикубике (zenzicubike), восьмая степень – зензизензизензике (zenzizenzizenzike).
А затем постепенно распространились символы, которые так хорошо знакомы всем нам сегодня.
Приблизительно в 1460 г. немецкий ученый Иоганн Видман впервые начал использовать знаки + и – для обозначения сложения и вычитания. В начале XVI в. Тарталья был одним из первых, кто начал использовать круглые скобки () в своих расчетах. В 1557 г. английский ученый Роберт Рекорд впервые использовал знак = для обозначения равенства. В 1608 г. голландский ученый Рудольф Снеллиус стал использовать запятую для разделения целой и дробной частей числа. В 1621 г. английский ученый Томас Хэрриот ввел знаки < > для обозначения соотношения двух чисел (больше/меньше).
В 1631 г. английский ученый Уильям Отред начал использовать значок × для умножения, а в 1647 г. первым обозначил знаменитую постоянную величину, открытую Архимедом, как π. Немецкий математик Иоганн Ран в 1659 г. впервые использовал ÷ для обозначения деления. В 1525 г. немецкий ученый Кристоф Рудольф ввел в обиход знак квадратного корня √, который в 1647 г. был дополнен горизонтальной полосой французским математиком Рене Декартом: √.
Конечно же, все это происходило не так последовательно и упорядоченно, как описано выше. В течение этого времени много других символов появлялось и исчезало. Некоторые из них использовались только один раз, другие – более активно. Между моментом, когда знак использовался впервые и его окончательным принятием всем математическим сообществом, зачастую проходили десятилетия. Так, даже спустя столетие после первого использования, + и – не стали универсальными знаками и многие математики продолжали использовать буквы P и M, инициалы латинских слов плюс (plus) и минус (minus), для обозначения сложения и вычитания.
И какова же роль Виета в этом? Деятельность французского ученого стала катализатором всеобщего принятия новой системы знаков. Написав «Исагогику», он тем самым начал обширную программу модернизации алгебры и заложил основу для использования букв алфавита в вычислениях. Его предложение гениально в своей простоте: обозначать неизвестные величины в уравнениях гласными, а известные числа – согласными.
Однако Рене Декарт впоследствии предложил иную систему: первые буквы латинского алфавита (a, b, c…) для обозначения известных величин и последние буквы (x, y и z) – для обозначения неизвестных. Этот подход используется сегодня большинством математиков, а буква «х» стала всеобщим обозначением чего-то неизвестного и таинственного.
Для того чтобы понять, как изменилась алгебра после появления всеобщего языка математики, рассмотрим уравнение:
Найдите число, которое при умножении на 5 дает 30.
В новой системе символов это будет записываться как: 5 × x = 30.
Обратите внимание, насколько короче запись! Это уравнение пример более широкой группы:
Найдите число, которое при умножении на число 1 дает число 2.
Это уравнение будет иметь вид: a × x = b.
Числа a и b взяты в начале алфавита, что, как мы знаем, означает, что это известные величины, зная которые, мы сможем вычислить х. И, как мы уже видели, уравнение этого типа решается путем деления второго известного члена на первый, другими словами: х = b ÷ a.
С этого момента математики начинают классифицировать уравнения по их типам и устанавливают правила для решения уравнений с буквенными обозначениями. Алгебра постепенно превращается в форму игры с собственными правилами. Решение нашего уравнения находится следующим образом: переходя из a × x = b в x = b ÷ a, буква a переходит с левой стороны от знака = направо, и умножение заменяется делением. Это одно из сформулированных правил: умножение можно заменить делением в другой части уравнения. Аналогичные правила применяются для сложения и вычитания, а также возведения в степень. Цель остается прежней: отыскать значение х.
Использование символов стало настолько эффективным, что алгебра начала быстро развиваться автономно от геометрии. Исчезла необходимость изображать умножение в виде прямоугольников или применять доказательство в виде мозаики. Теперь все сводилось к определению x, y и z! Более того, стремительное развитие эффективности алгебраических конструкций с использованием букв в скором времени приведет к тому, что уже геометрия будет опираться на алгебраические доказательства.
Французский математик Рене Декарт будет основоположником эффективного способа решения геометрических задач алгебраическими методами с использованием системы осей координат.
Декартова система координат
Идея Декарта была одновременно элементарной и гениальной: начертить две размеченные линии, горизонтальную и вертикальную, с тем чтобы идентифицировать каждую геометрическую точку координатами по двум осям. Рассмотрим, например, следующую точку А:
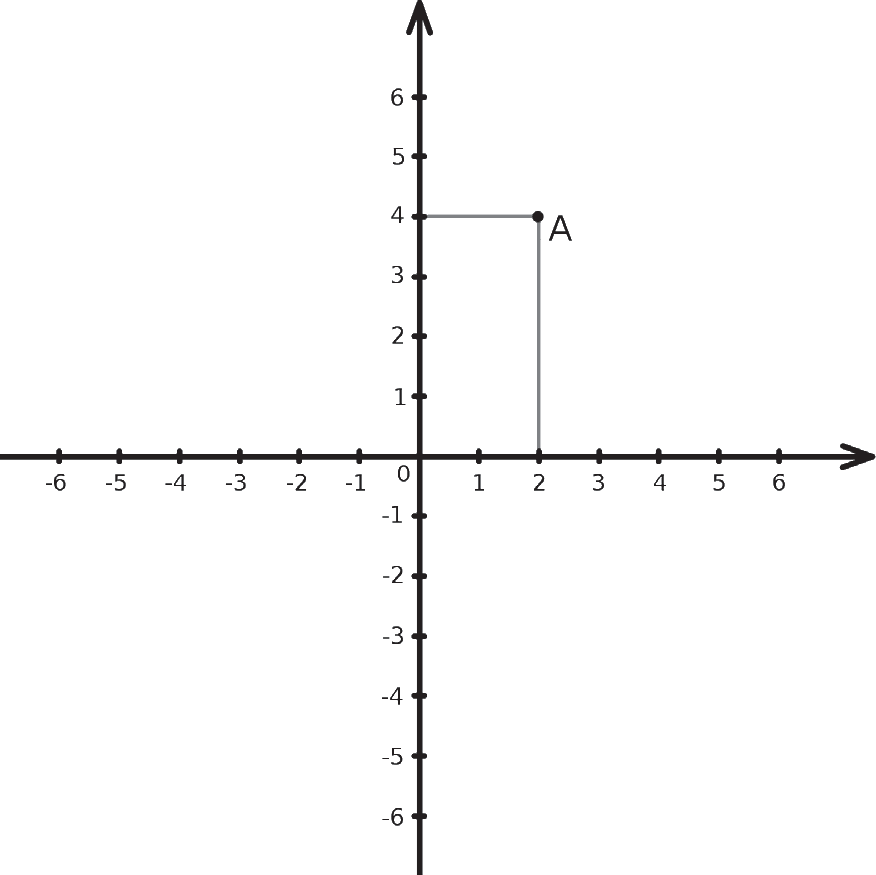
Точка находится на отметке 2 горизонтальной оси и 4 – вертикальной оси. Следовательно, ее координаты равны 2 и 4. С помощью этого метода становится возможным представлять каждую геометрическую точку двумя числами и, наоборот, находить точку для каждой пары чисел.С момента своего возникновения геометрия и числа всегда имели тесные связи, но с появлением прямоугольной системы координат две эти дисциплины стали неразрывны. С того времени любая геометрическая задача могла решаться алгебраически, а алгебраическая задача – геометрически.Рассмотрим, например, следующее уравнение первой степени: х = у + 2. Это уравнение с двумя неизвестными: необходимо найти х и у. Например, можно заметить, что х = 2 и у = 4 образуют решение, так как 2 + 2 = 4. Далее ясно, что числа 2 и 4 – это координаты точки А. Таким образом, можно представить это решение геометрически как точку.На самом деле уравнение х + 2 = у имеет бесконечное количество решений. Например, пары чисел х = 0 и у = 2 или х = 1 и у = 3. Для любого значения х находится соответствующий у путем добавления 2. Теперь мы можем отметить в нашей системе координат все точки, соответствующие этим решениям. Таким образом, мы получим следующий график.
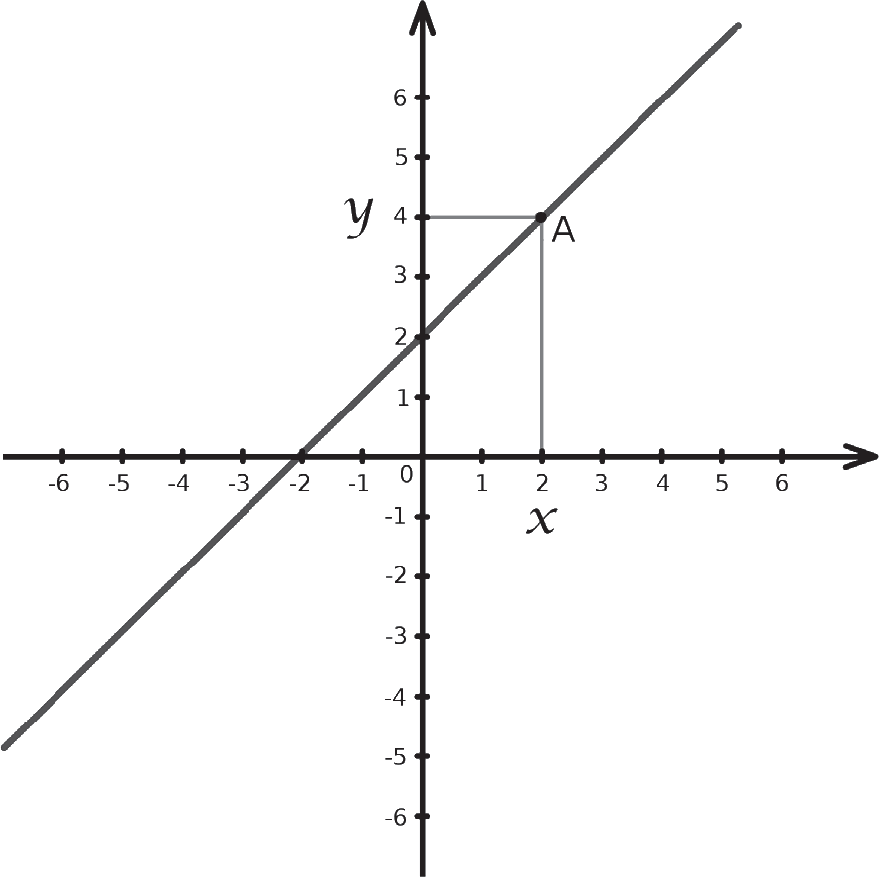
Прямая линия! Решения формируют идеально прямую линию. Нет ни одного из них, которое отклонялось бы от этого правила. В прямоугольной системе координат линия является геометрическим решением уравнения, а уравнение – алгебраическим представлением прямой линии. Два объекта слились воедино, и сегодня нередко можно услышать, как математики называют прямую линию х + 2 = y. Давая одни и те же имена разным вещам, алгебра и геометрия в действительности становятся единой дисциплиной.Такая взаимозависимость привела к тому, что геометрические явления могут быть описаны алгебраическим языком и наоборот. Например, то, что называется «серединой» в геометрии, именуется «средним» в алгебре. Возьмем точку А с координатами 2 и 4 и соединим ее с точкой B с координатами 4 и 6. Для того, чтобы найти середину отрезка, соединяющего А и В, достаточно найти средние значения координат. Первые координаты А и В равны 2 и 4, соответственно, из чего можно сделать вывод о том, что первая средняя координата равна среднему значению этих двух чисел: (2 + 4) / 2 = 3. Аналогично можно найти среднее значение по вертикальной оси: (4 + (–6)) / 2 = –1. Таким образом, координаты середины отрезка равны 3 и –1, в чем можно убедиться, отметив эту точку на графике:
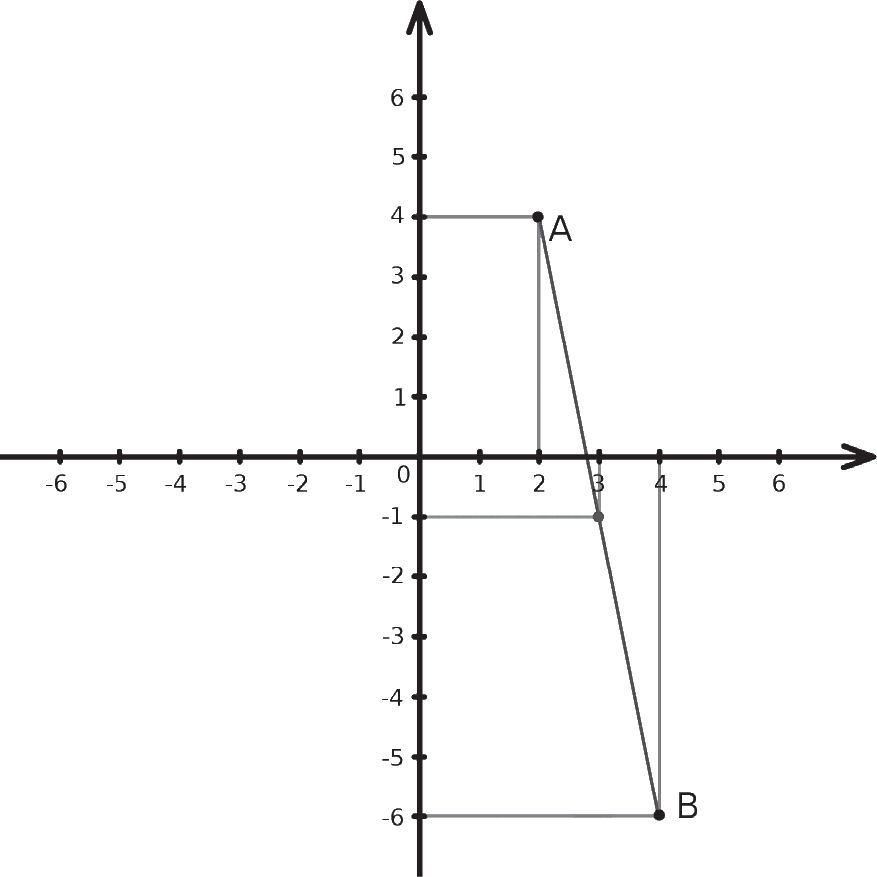
В словаре соответствий терминов из алгебры и геометрии окружность обозначает квадратное уравнение, точки пересечения двух окружностей – систему уравнений, а теорема Пифагора, тригонометрические конструкции и разделение на мозаичные части трансформируются в различные буквенные формулы.Подводя итоги, можно сделать вывод, что в дальнейшем для решения геометрических задач не было необходимости изображать фигуры: алгебраические расчеты окончательно заняли свое место в математике, что значительно упростило и ускорило решение задач!
В последующие века использование прямоугольной системы координат способствовало достижению значительных успехов в развитии математики.
Одним из наиболее важных среди них было, несомненно, решение вопроса гипотезы, волновавшей умы математиков еще со времен Античности: определение квадратуры круга.
Можно ли с помощью линейки и циркуля начертить квадрат и круг, равные по площади? Вспомните, как еще более трех тысяч лет назад писец Ахмес уже пытался решить этот вопрос. После него разгадку безуспешно искали в Древнем Китае и Греции, но вопрос оставался на протяжении веков одной из величайших математических загадок, ответа на которую не было найдено.
В прямоугольной системе координат прямые линии, проведенные с помощью линейки, становятся линейными уравнениями, в то время как окружность, начерченная циркулем, может быть представлена в виде квадратного уравнения. С алгебраической точки зрения вопрос о квадратуре круга, таким образом, сводится к вопросу о том, можно ли найти такие уравнения первой и второй степени, решениями которых будет число π? Благодаря этой формулировке исследования возобновились, но вопрос все равно оставался сложным.
Только в 1882 г. немецкий математик Фердинанд фон Линдеман нашел окончательный ответ на этот вопрос. Нет, решением уравнений первой и второй степени не будет число π, и найти квадратуру круга невозможно. Таким образом, была решена проблема, которая до этого времени не поддавалась ни одному математику.
Прямоугольная система координат может легко быть расширена до пространственной геометрии. В трехмерной системе координат каждая точка будет иметь уже три координаты, и алгебраические методы могут быть применены к ним таким же образом.
Все становится несколько сложнее, когда мы переходим к четвертому измерению. С точки зрения геометрии невозможно представить себе фигуру в четырех измерениях, так как мы живем в трехмерном мире. В алгебре, однако, это не представляет сложности: значение координаты четвертого измерения – это все лишь четвертая строчка в координатной записи. И все алгебраические методы применимы в четырехмерном пространстве аналогичным образом. Например, если мы рассмотрим точки А и В, координаты которых равны 1, 2, 3 и 4 для первой точки и 5, 6, 7 и 8 для второй соответственно, можно без проблем найти среднее значение этих чисел: их координаты будут равны 3, 4, 5 и 6. Четырехмерная геометрия, в частности, использовалась в XX в. при формулировании теории относительности Альберта Эйнштейна, который станет использовать четвертую координату для моделирования времени.
Можно продолжить расширять количество измерений. Пять значений в определении координаты точки будут означать, что эта точка находится в системе, состоящей из пяти измерений. Добавьте еще одну координату, и количество измерений возрастет до шести. Этот процесс можно продолжать бесконечно. Тысяча чисел в обозначении координат точки будет указывать, что она определена в системе, состоящей из тысячи измерений.
На этом уровне аналогия может показаться простой игрой слов и вызывать улыбку, т. к. может показаться, что такие системы не имеют практической пользы. Задумайтесь еще раз. Многомерные системы координат имеют многочисленные варианты применения, включая статистику, в задачи которой входит изучение больших массивов числовых данных.
При изучении, например, демографии может потребоваться определить количественные характеристики различных групп населения, такие как рост, вес или тип питания представителей каждой из них, а также отклонения от среднего значения. Для того чтобы изобразить это геометрически, потребуется определить расстояние между двумя точками: первой, соответствующей данным по каждому человеку, и второй, характеризующей среднее значение. Таким образом, количество координат соответствует количеству лиц в группе. Затем осуществляется расчет с помощью прямоугольных треугольников, для чего можно применить теорему Пифагора. Статистик, вычисляющий отклонения от среднего значения в группе, состоящей из тысячи людей, часто, не подозревая об этом, использует теорему Пифагора в пространстве, состоящем из тысячи измерений! Этот метод также применяется в эволюционной биологии, чтобы вычислить генетическую разницу между популяциями животных. Измеряя по формулам, взятым из геометрии, расстояния между генами, обозначенные в виде списков чисел, становится возможным установить относительную близость различных видов и постепенно построить схему генетического родства всех живых организмов.
Можно даже проводить исследования с бесконечным списком чисел, то есть анализировать точки в пространстве бесконечной размерности! На самом деле мы уже сталкивались с ними: это такие числовые последовательности, как, например, последовательность Фибоначчи. Изучая динамику роста популяции кроликов, итальянский математик, сам того не подозревая, занимался исследованиями в пространстве бесконечной размерности! Именно эта геометрическая интерпретация позволила математикам XVIII в. найти еле уловимую связь между последовательностью Фибоначчи и золотым сечением.
Назад: 11 Воображаемые миры
Дальше: 13 Мировой алфавит

