Если нравственные чувства так полезны, то почему тогда в мире так много нечестных людей? Какие силы помешали нравственным чувствам вытеснить чувства менее благородные, которые так же очевидно свойственны человеческой природе? Чтобы сфокусироваться на этих вопросах, давайте изучим специфический пример проблемы обмана.

Вернемся к примеру с рестораном. И у Смита, и у Джонса есть выбор — обманывать или нет. Выбор этот предполагает четыре возможные комбинации поведения. Для большей наглядности предположим, что выигрыши для этих комбинаций представлены в табл. III. 1. Термины «предать» и «сотрудничать» означают соответственно «обманывать» и «не обманывать».

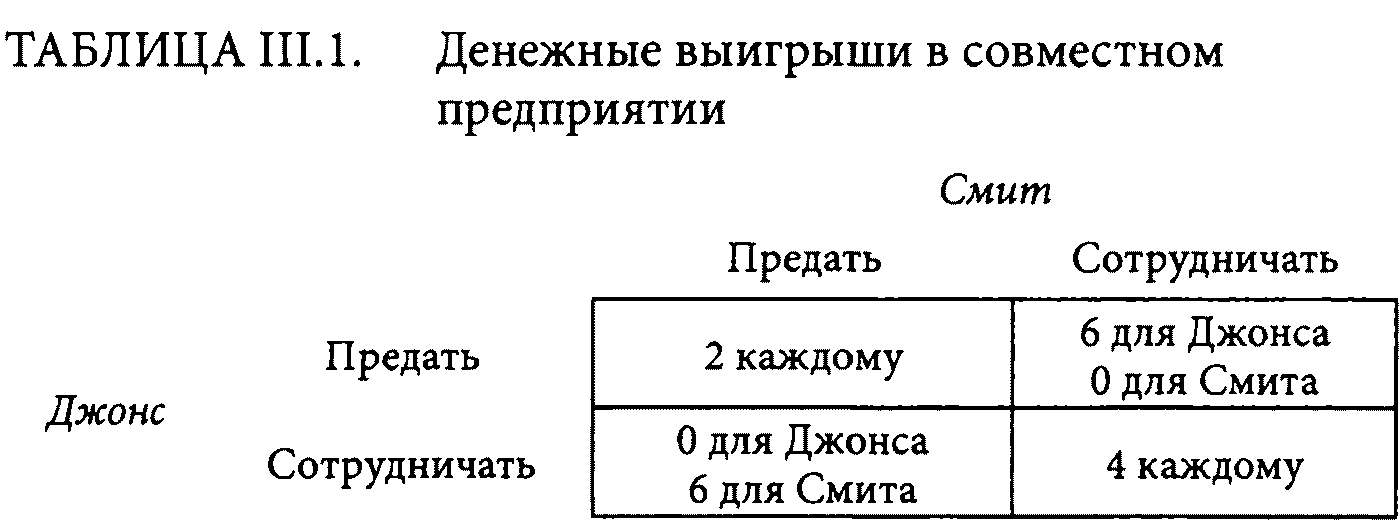
Выигрыши в табл. III. 1 — те же самые, что мы видели в таблице для материальной дилеммы заключенного в главе II. Как и раньше, преобладающая стратегия — предать своего партнера. Джонс получит более высокий выигрыш, если предаст, чего бы ни делал Смит, и то же самое верно для Смита. Если Джонс считает, что Смит ведет себя эгоистически, он предскажет, что Смит предаст. И пусть только ради того, чтобы защитить себя, он скорее всего будет вынужден тоже предать. Когда оба предадут друг друга, каждый получает выигрыш в 2 единицы. Неприятность, как со всеми такими дилеммами, в том, что оба легко могли бы выиграть больше. Если бы они сотрудничали, каждый бы получил выигрыш в 4 единицы.

Теперь предположим, что у нас не только Смит и Джонс, но более крупная популяция. Пары людей снова создают совместные предприятия, и отношения между поведением и выигрышами для членов каждой пары — снова такое же, как приведено в табл. III. 1. Предположим далее, что каждый в популяции относится к одному из двух типов — сотрудничающему или предателю. Сотрудничающий — тот, кто, возможно, благодаря интенсивному культурному принуждению развил генетически передаваемую способность испытывать нравственное чувство, склоняющее его к сотрудничеству. Предатель — тот, кто либо лишен этой способности, либо не смог ее развить.

В этой схеме сотрудничающие — жесткие альтруисты в том смысле, в каком это описывалось в главе II. Они воздерживаются от обмана, даже когда нет возможности разоблачения, и это поведение очевидным образом противоречит их интересам. Предатели, в свою очередь, — настоящие оппортунисты. Они всегда делают выбор в пользу того, что максимизирует их личный выигрыш. Наша задача — определить, что произойдет, когда людей из двух этих групп столкнут в конкурентной борьбе друг против друга. Какие результаты покажет каждый тип, зависит от того, можно ли (а если да, то как) различить эти две группы. Я по очереди рассмотрю несколько случаев.

Прежде всего, предположим, что сотрудничающие и предатели выглядят совершенно одинаково. В такой популяции два этих типа будут образовывать случайные пары. Естественно, предел желаний для сотрудничающих (и по той же причине для предателей) — образовать пару с другим сотрудничающим, но здесь у них не будет выбора. Поскольку все похожи друг на друга, им придется действовать на свой страх и риск. Предполагаемые выигрыши и для сотрудничающих, и для предателей, таким образом, зависят от вероятности образования пары с сотрудничающим, которая в свою очередь зависит от доли сотрудничающих в популяции.

Предположим, например, что популяция почти полностью состоит из сотрудничающих. Тогда сотрудничающий почти наверняка получит в качестве партнера другого сотрудничающего, и потому их будет ожидать выигрыш в 4 единицы. Редкий предатель в такой популяции точно так же почти наверняка образует пару с сотрудничающим и может ожидать выигрыш приблизительно в 6 единиц. (Незадачливый партнер предателя, конечно, получит нулевой выигрыш, но его единичная неудача незначительно скажется на среднем выигрыше для сотрудничающих как группы.)

Или же предположим, что популяция состоит наполовину из сотрудничающих, наполовину из предателей. У каждого в ней равные шансы образовать пару как с сотрудничающим, так и с предателем — 50 на 50. У сотрудничающих будут равные шансы получить как нулевой выигрыш, так и 4 единицы, что дает им средний выигрыш в 2 единицы. Предатели, в свою очередь, имеют равные шансы получить 2 или 6 единиц, так что для них средний выигрыш составит 4 единицы. В целом средние выигрыши для каждого типа будут расти с ростом доли сотрудничающих в популяции: у сотрудничающих — потому что меньше вероятность, что ими воспользуется предатель, у предателя — потому что у него будет больше шансов найти сотрудничающего, которого он может использовать. Точное соотношение выигрышей из данного примера приводится на рис. III.2.

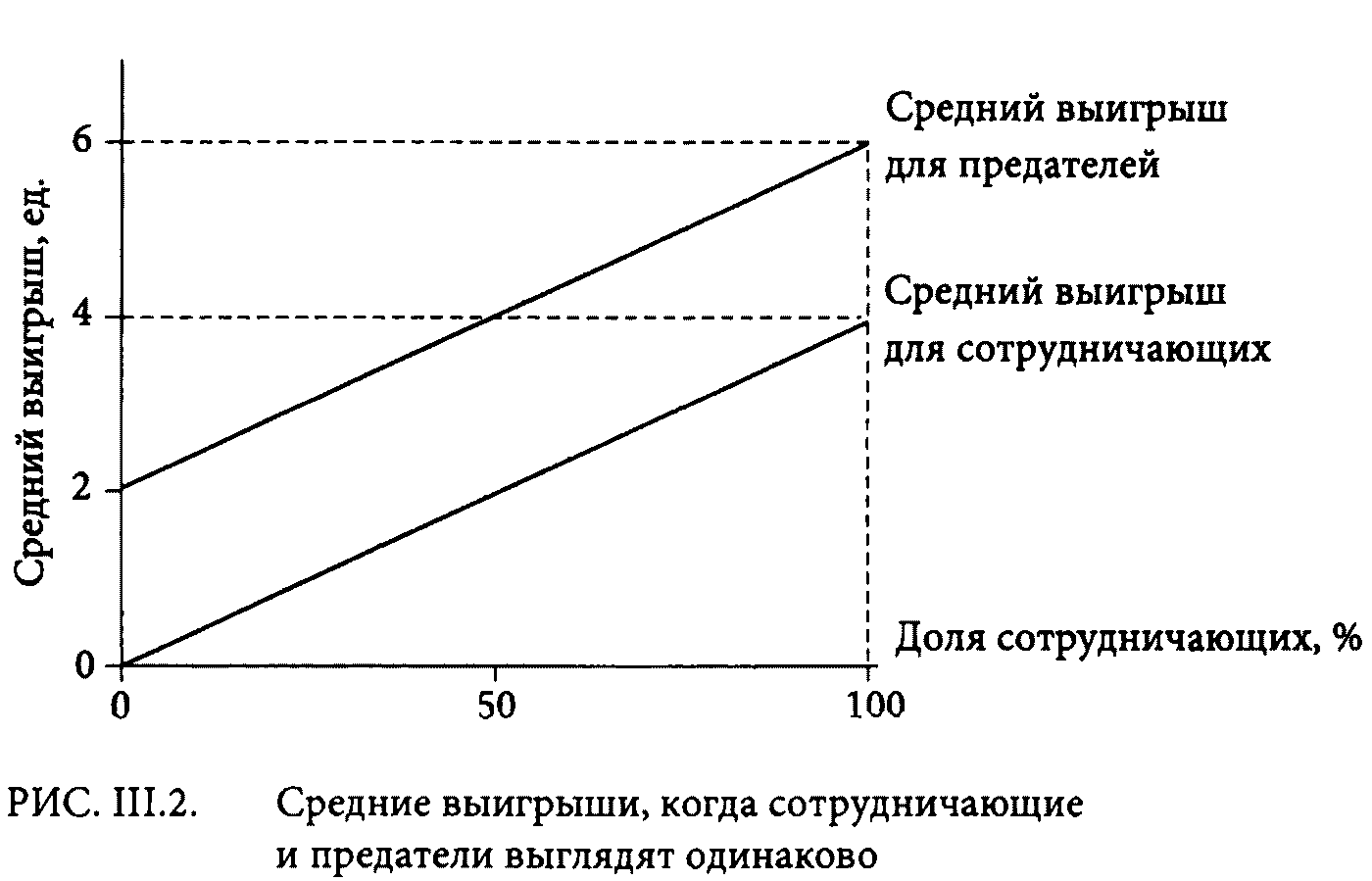
Если сотрудничающие и предатели внешне ничем не отличаются друг от друга, как будет эволюционировать популяция с течением времени? В эволюционных моделях каждый индивид воспроизводится пропорционально его среднему выигрышу: те, у кого материальный выигрыш больше, имеют ресурсы для производства большего числа потомства. Поскольку предатели всегда будут получать здесь более высокий средний выигрыш, их доля в популяции со временем вырастет. Сотрудничающие, даже если вначале они составляют подавляющее большинство в популяции, таким образом, обречены на исчезновение. Когда сотрудничающие и предатели выглядят одинаково, истинного сотрудничества возникнуть не может. Грубо говоря, этот случай воплощает в себе традиционное социобиологическое описание поведения.

Теперь предположим, что все, как и раньше, за исключением того, что сотрудничающие и предатели совершенно не похожи друг на друга. Представим, что сотрудничающие рождаются с красной С на лбу, предатели — с красным П. Внезапно картина полностью меняется. Сотрудничающие теперь могут взаимодействовать исключительно друг с другом и рассчитывать на выигрыш в 4 единицы. Сотрудничающему никогда не понадобится взаимодействовать с предателем. Предателям ничего не остается, как взаимодействовать друг с другом, в результате чего они получают выигрыш всего в 2 единицы.

Поскольку все элементы случайности были исключены из процесса взаимодействия, выигрыши больше не зависят от доли сотрудничающих в популяции (см. рис. III.3). Сотрудничающие всегда получают 4 единицы, предатели всегда получают 2.

На этот раз более крупные выигрыши сотрудничающих дают им возможность создавать более крупные семьи, что означает, что их доля в популяции будет неуклонно расти. Когда сотрудничающих легко распознать, с угрозой исчезновения сталкиваются предатели.

Однако предателям не понадобится «уходить безмолвно в ночи край». Предположим, появляется группа предателей-мутантов, которые ведут себя точно так же, как другие предатели, но у которых на лбу написано красным не П, а С. Поскольку эта отдельная группа предателей выглядит точно так же, как сотрудничающие, последние не могут их дискриминировать. Каждый самозванец, таким образом, имеет такие же шансы вступить во взаимодействие с сотрудничающим, как и настоящий сотрудничающий. Это, в свою очередь, означает, что предатели-мутанты получат более высокие выигрыши, нежели кооператоры.

Предатели-немутанты — продолжающие носить на лбу П — будут иметь более низкие выигрыши, чем обе эти группы и, как и раньше, будут обречены на вымирание. Но пока сотрудничающие каким-либо образом не приспособятся, им грозит та же судьба. Когда предатели могут в точности имитировать отличительные черты сотрудничающего безо всяких затрат или отлагательств, эти черты теряют свою различительную функцию. Сотрудничающие и выжившие предатели снова выглядят одинаково, что грозит гибелью сотрудничающим.

Способность к адаптации, конечно, не является монополией предателей. Если случайные мутации изменят отличительные черты сотрудничающих, предатели будут иметь дело с движущейся мишенью. Предположим, что красное С, по которому сотрудничающие первоначально узнавали друг друга, со временем превратилось в красноватый цвет лица — своего рода румянец — и что у некоторых предателей тоже есть такой румянец. Но поскольку сотрудничающие искренне испытывают эмоции, которые мотивируют на сотрудничество, у них этот румянец в среднем более сильный.

В целом мы могли бы ожидать континуума интенсивности румянца для обеих групп. Ради простоты, однако, предположим, что цвет лица имеет два четких типа: 1) сильный румянец и 2) легкий румянец. Люди с сильным румянцем — сотрудничающие, со слабым — предатели. Если эти два типа можно различить с первого взгляда, предатели снова обречены. Но предположим, что нужно приложить какие-то усилия для определения степени интенсивности румянца. Для большей конкретности предположим, что проверка стоит 1 единицу. Для людей, которые заплатят эту цену, завеса будет приподнята: сотрудничающих и предателей можно будет различить со 100%-й точностью. Для тех, кто не станет платить 1 единицу за проверку, два этих типа останутся совершенно одинаковыми.

Чтобы увидеть, что случилось на этот раз, предположим, что выигрыши снова такие же, как приводились в табл. III.1, и рассмотрим решения, которые должен принимать сотрудничающий, пытающийся решить, платить ли за проверку. Если он за нее заплатит, то гарантированно будет иметь дело с другим сотрудничающим и тем самым получит выигрыш 4-1=3 единицы. Если нет, его выигрыш неопределён. Сотрудничающие и предатели будут казаться ему совершенно одинаковыми, и ему придется действовать на свой страх и риск. Если ему попадется другой сотрудничающий, он получит 4 единицы. Но если ему попадется предатель, он ничего не получит. Имеет ли смысл платить 1 единицу за проверку, зависит от вероятности этих двух исходов.

Предположим, что доля сотрудничающих в популяции — 90%. Не заплатив за проверку, сотрудничающий будет иметь дело с другим сотрудничающим 90% времени, с предателем — только 10%. Его выигрыш, таким образом, будет в среднем составлять (0,9 х 4) + (0,1 х 0) = 3,6. Поскольку это больше, чем чистый выигрыш в 3 единицы, который он получил бы заплатив за проверку, ясно, что лучше не платить.

Теперь предположим, что доля сочувствующих в популяции не 90, а 50%. Если наш сочувствующий не платит за проверку, его шансы столкнуться с предателем 50 на 50. Его средний выигрыш будет составлять всего 2 единицы, или на 1 единицу меньше, чем если бы он заплатил за проверку. При таком раскладе ему, очевидно, лучше заплатить за проверку.

Цифры в этом примере предполагают «точку безубыточности», когда доля сотрудничающих в популяции — 75%. В этом случае сотрудничающий, не заплативший за проверку, имеет 75% шансов получить выигрыш в 4 единицы и 25% шансов получить нулевой выигрыш. Его средний выигрыш, таким образом, 3 единицы, такой же, как если бы он заплатил за проверку. Когда доля сотрудничающих в популяции ниже 75%, ему всегда лучше заплатить за проверку; а когда доля сотрудничающих выше 75%, для него всегда лучше за нее не платить.

С учетом этого правила мы теперь можем сделать некоторые предположения, как популяция будет развиваться со временем. Когда доля сотрудничающих в ней ниже 75%, все сотрудничающие будут платить за проверку и получать выигрыш в 3 единицы, сотрудничая друг с другом. Не в интересах предателей нести эти расходы, потому что прозорливые сотрудничающие все равно не станут с ними взаимодействовать. Предателям ничего не останется, как взаимодействовать друг с другом и получать выигрыш всего в 2 единицы. Таким образом, если мы начинаем с доли сотрудничающих в популяции ниже 75%, сотрудничающие будут получать более высокий средний выигрыш, что означает, что их доля в популяции будет расти.

В популяциях, состоящих из более чем 75% сотрудничающих, ситуация обратная. Теперь нет смысла платить за проверку. Сотрудничающие и предатели будут, таким образом, взаимодействовать случайно, что означает, что у предателей будет более высокий средний выигрыш. Это различие в выигрышах, в свою очередь, будет вести к тому, что доля сотрудничающих в популяции будет сокращаться.

Для величин, предполагаемых в этом примере, средние графики выигрышей для двух групп представлены на рис. III.4. Как отмечалось, прямая сотрудничающих проходит выше прямой предателей для доли менее 75%, но ниже — для более высоких долей. Резкий разрыв в прямых предателей отражает тот факт, что слева от 75% все сотрудничающие платят за проверку, тогда как справа от 75% — никто. Как только доля сотрудничающих в популяции превышает 75%, предатели неожиданно получают доступ к своим жертвам. Правило эволюции, напомним, в том, что более высокие относительные выигрыши ведут к росту соответствующей доли населения. Это правило ясно показывает, что в данном примере популяция придет в равновесие на цифре 75% сотрудничающих.

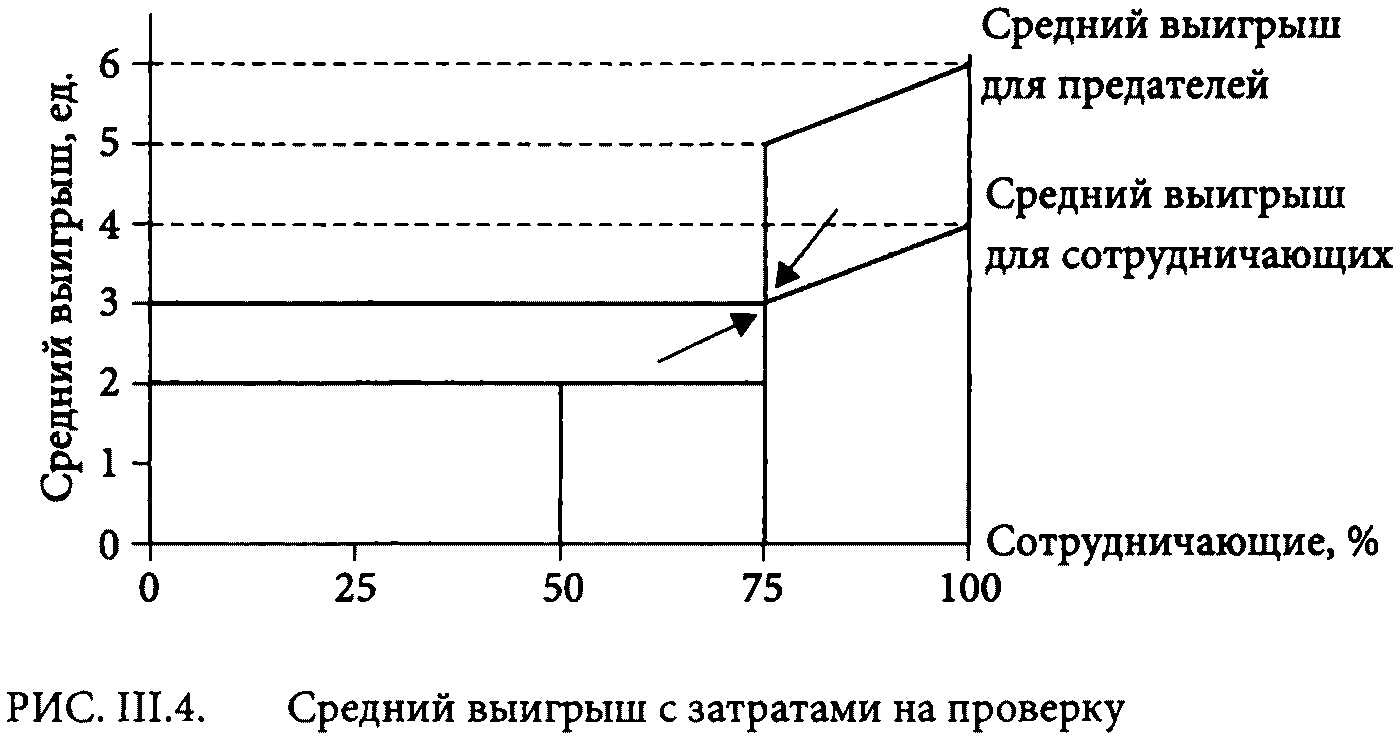
Однако в этих 75% нет ничего волшебного. Если бы, например, цена проверки была выше 1 единицы, доля сотрудничающих в популяции была бы меньше. Сокращение выигрыша, когда сотрудничающие объединяются друг с другом, возымела бы такое же действие на равновесие долей населения. Суть этого примера в том, что, когда есть затраты на проверку, будет создаваться давление, которое подтолкнет популяцию к какому-то устойчивому смешению сотрудничающих и предателей. Как только это смешение в популяции установится, члены обеих групп будут иметь один и тот же средний выигрыш и потому будут иметь равные шансы на выживание. Иными словами, есть экологическая ниша для обеих групп. Этот результат резко противоречит традиционному социобиологическому результату, согласно которому выживает только оппортунизм.