Перейдем от масштабов галактик, т. е. астрономических, к масштабам космологическим. Это позволяет решить несколько задач. Во-первых, получить независимые оценки Ωm – плотности материи, выраженной в процентах от критической плотности. Во-вторых, разделить вклады темной и барионной материй. Для этого вводится аналогичный параметр Ωb – отношение плотности барионной материи к критической. Понятно, что плотность небарионной темной материи в процентах от критической плотности будет равна Ωm – Ωb. В-третьих, кроме этого, естественно получаются оценки параметра ΩΛ – отношения плотности энергии, связанной с космологической постоянной, к критической плотности энергии. В настоящее время космологическая постоянная рассматривается как один из частных случаев темной энергии, о которой мы расскажем ниже.

Еще до открытия реликтового излучения космологи мечтали о двух типах космических объектов, которые позволили бы им разобраться с геометрией пространства-времени, в частности определить знак кривизны Вселенной. Первый тип объектов получил жаргонное название «стандартная свеча». Это объекты, которые обладают одинаковой светимостью, но при этом находятся на очень разных расстояниях от Земли. Второй тип объектов называется стандартной линейкой и имеет одинаковые линейные размеры. Зачем эти объекты были так нужны? Дело в том, что в искривленном пространстве, как мы уже упоминали в разделе 2.5, понятие расстояния становится неоднозначным. Вводятся несколько видов расстояний, которые связаны друг с другом через кривизну пространства.

Имея стандартную свечу, мы можем ввести так называемое фотометрическое расстояние. По определению, это расстояние, на которое нужно в плоском пространстве отнести источник света, чтобы получить наблюдаемый поток света. Его отличие от обычного расстояния связано с двумя факторами. Первый из них связан с тем, что освещенность поверхности обратно пропорциональна квадрату расстояния до точечного источника света. Это справедливо только для плоского пространства. В пространстве с положительной кривизной поверхность сферы радиуса r меньше чем 4πr2. Соответственно, освещенность будет падать медленнее, чем r–2. Понятно, что в пространстве с положительной кривизной, где поток больше, чем в плоском пространстве, благодаря только первому фактору, фотометрическое расстояние будет меньше, чем в плоском. Соответственно, в пространстве отрицательной кривизны, где площадь поверхности сферы больше чем 4πr2, фотометрическое расстояние было бы больше, чем в плоском пространстве при одинаковых потоках.

Второй фактор связан с тем, что свет от удаленных источников был излучен в более ранней Вселенной и за время распространения длина его волны увеличилась в 1 + z раз. Соответственно, энергия фотонов, пропорциональная частоте, уменьшилась в 1 + z раз. Кроме того, в 1 + z раз увеличилось время между приходами фотонов. В результате в формуле для потока света, наблюдаемого на Земле, возникает множитель (1 + z)–2, что увеличивает фотометрическое расстояние в 1 + z раз.

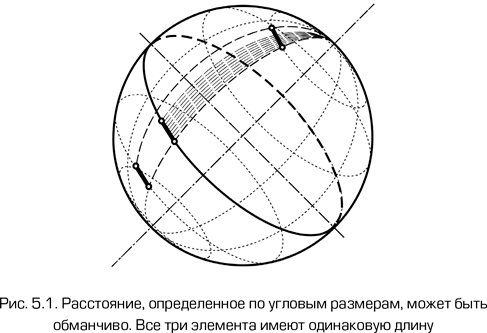
Имея стандартную линейку, мы можем ввести понятие расстояния, определенного по угловым размерам. В плоском пространстве объект длиной l на расстоянии r >> l виден под углом φ = l/r в радианной мере. Соответственно, расстояние может быть определено по формуле r = l/φ. В кривом пространстве все куда сложнее. Рассмотрим поверхность сферы, например Земли (см. рис. 5.1). Пусть наблюдатель находится на Северном полюсе и измеряет угловые размеры метровой линейки, расположенной точно вдоль параллели. Поскольку в двумерном пространстве с положительной кривизной свет распространяется по большому кругу, фактически нам необходимо вычислить разность долгот западного и восточного концов линейки. По мере удаления линейки от наблюдателя ее угловые размеры будут уменьшаться, достигнут минимума на экваторе, а затем снова начнут увеличиваться при приближении к Южному полюсу. При этом угловой размер линейки на экваторе будет равен 2π×1 м/40 000 км. В плоском же пространстве угловой размер линейки будет равен 1 м/10 000 км. Таким образом, в пространстве с положительной кривизной минимальный угловой размер линейки будет в π/2 ≈ 1,57 раз больше, чем в плоском, независимо от величины кривизны. Соответственно, расстояние по угловым размерам будет меньше, чем в плоском пространстве. В пространстве с отрицательной кривизной ситуация будет обратной: расстояние по угловым размерам будет больше, чем в плоском пространстве.

Кроме этого, у нас существует уже введенное расстояние по красному смещению, которое легко определяется для любого астрономического объекта по его спектру. Имея стандартную свечу, мы можем построить график зависимости фотометрического расстояния от расстояния по красному смещению, который даст нам необходимую информацию о свойствах пространства. Аналогично, имея стандартную линейку, мы можем построить зависимость расстояния по угловым размерам от расстояния по красному смещению. Как видим, достаточно иметь либо свечу, либо линейку. Если же имеется и то и другое, мы можем получить две независимые оценки кривизны Вселенной.

Раньше в качестве стандартных свечи и линейки пытались использовать галактики, предполагая, что их светимость и линейные размеры постоянны. Эти попытки не увенчались успехом, что не удивительно, учитывая, что галактики довольно сильно отличаются друг от друга. В настоящее время мы имеем куда более совершенных кандидатов на роль стандартной свечи и стандартной линейки.

В качестве стандартной свечи используются взрывы сверхновых типа Ia. Сверхновой называется катастрофический этап в жизни звезды, когда она в течение короткого промежутка времени излучает со светимостью, сравнимой со стандартной светимостью целой галактики. Название пришло из трактата Тихо Браге «О новой звезде» (De stella nova), описавшего подобную вспышку, которую он наблюдал в 1572 г. Отсюда и пошли термины «новая» и «сверхновая».

Вспышки, как правило, обозначаются буквами SN, за которыми следует год их наблюдения, а иногда и латинская строчная буква, чтобы различать сверхновые, обнаруженные в том же году. Сверхновую, которую наблюдал Тихо Браге, обозначают SN 1572.

Вспышки сверхновых – довольно редкие события. В нашей Галактике они происходят нечасто, а наблюдать их астрономы могут еще реже – в среднем 3–4 раза в тысячелетие. В истории человечества было только пять подтвержденных наблюдений сверхновых в нашей галактике Млечный Путь, в последний раз это произошло в 1604 г., по иронии судьбы, всего за несколько лет до изобретения телескопа Галилео Галилеем в 1610 г. Следующая сверхновая наблюдалась в 1885 г. в галактике Андромеды. Все последующие вспышки сверхновых тоже наблюдались в других галактиках.

Тем не менее астрономы составили список звезд в нашей Галактике, которые в ближайшее время могут стать сверхновыми. Наиболее близкими к нам являются белый карлик IK Пегаса B, находящийся на расстоянии всего 150 св. лет, и красный гигант Бетельгейзе, находящийся на расстоянии 640 св. лет. Карлик IK Пегаса B, также известный под именем HR 8210, превратится в сверхновую типа Ia, а Бетельгейзе – в сверхновую типа IIn. Несмотря на то что минимальное безопасное расстояние от сверхновой порядка 200 св. лет, опасаться нет причин. Во-первых, «в ближайшее время» в астрономических масштабах может означать сотни миллионов лет, а во-вторых, IK Пегаса B к этому времени отдалится от Земли на значительное расстояние. Впрочем, для космологии куда более интересны взрывы сверхновых на больших расстояниях с z > 0,3. На данный момент наиболее далекие из наблюдаемых сверхновых имеют z-фактор немного больше 1.

Всего различают пять типов сверхновых, обозначенных римскими цифрами от I до V. Эти типы разделены на подтипы, которые обозначены строчными латинскими буквами, например тип Ia обозначается как SN Ia, а тип IIn – как SN IIn. К таким вспышкам приводят два различных механизма.

Время от времени массивные звезды (тяжелее, чем приблизительно 10 масс Солнца), выработавшие водород в ядре, коллапсируют и взрываются, сбрасывая оболочку. Эффективность термоядерного синтеза падает, и давление излучения больше не может скомпенсировать силу гравитации. После этого звезда коллапсирует, т. е. быстро сжимается, давление и температура резко возрастают, и синтез вновь запускается, используя теперь в качестве сырья еще и гелий и более тяжелые элементы. Этот процесс является единственным источником элементов тяжелее свинца во Вселенной. Если дополнительного давления, создаваемого реакцией синтеза, достаточно, чтобы преодолеть сжатие, то происходит взрыв сверхновой, который выбрасывает внешние слои звезды на большие расстояния; в противном случае звезда коллапсирует дальше, превращаясь в черную дыру или нейтронную звезду. Этот механизм называется коллапсом ядра и является причиной возникновения всех типов сверхновых (в зависимости от параметров исходной звезды), за исключением самых мощных сверхновых типа Ia. Мы упоминали об этом в подразделе 3.8.2.

Сверхновые типа Ia образуются совершенно иначе, механизм их образования называется тепловым убеганием. В отличие от коллапса ядра, свойственного очень массивной звезде, тепловое убегание происходит с двойной системой, содержащей белый карлик – небольшую и чрезвычайно горячую звезду. Когда расстояние между звездами достаточно мало, белый карлик начинает красть вещество у своего компаньона, увеличивая свою массу за счет этого вещества, перетекающего от одной звезды к другой.

Когда давление и температура ядра белого карлика превысит порог, после которого начинают сливаться ядра углерода, этот процесс синтеза выделяет еще больше тепла. В результате происходит взрыв сверхновой типа Ia, полностью разрушающий ядро с высвобождением огромного количества энергии, – весьма живописная иллюстрация того, что чревоугодие действительно является смертным грехом. Важность появления таких сверхновых для внегалактической астрономии связана с тем, что в максимуме они имеют практически одну и ту же светимость, соответствующую абсолютной звездной величине, равной –19,3, что примерно в 5 млрд раз ярче Солнца.

Тем не менее существует определенный скептицизм, вытекающий из исторического опыта использования цефеид в качестве индикаторов расстояния. Первый потенциальный источник беспокойства связан с тем, что особо далекие сверхновые типа Ia могут не иметь такого же пика светимости из-за того, что их звезды-предшественники должны быть значительно моложе. Однако работа механизма теплового убегания не должна зависеть от возраста звезды. Другая проблема заключается в том, что наблюдатель может неправильно классифицировать некоторые вспышки существенно более слабых сверхновых типа Ib или Ic как сверхновую типа Ia из-за сходства их спектров. Однако такие ошибки были бы отчетливо видны на графике зависимости фотометрического расстояния от красного смещения как явные выбросы. Третья проблема состоит в том, что система из двух белых карликов может иметь широкий спектр пиковых светимостей в зависимости от масс обоих компонентов. Это соображение может скорее поставить под сомнение объяснение механизма вспышек сверхновых типа Ia, но не сам факт, что они имеют одинаковые пиковые светимости, который был установлен статистически по данным наблюдений.

Как происходит поиск вспышек сверхновых? Несмотря на всю масштабность этих событий, они случаются настолько далеко, что до Земли доходят в виде кратковременного появления слабо светящегося объекта. Типичная продолжительность вспышки сверхновой – около 20 дней. Из-за расширения Вселенной наблюдаемая продолжительность в 1 + z раз больше. Уже одно это подтверждает факт расширения Вселенной.

Астрономы ежедневно делают снимки всего неба и сравнивают их со вчерашними. Если на снимках появляется новый точечный светящийся объект и проверка показывает, что это не ошибка и не известный переменный объект, то с большой вероятностью наблюдается либо вспышка сверхновой, либо событие микролинзирования. И то и другое очень интересует астрономов разных специализаций и требует продолжительного наблюдения этого объекта. Наблюдение должно вестись непрерывно днем и ночью, поэтому его нужно проводить в обсерваториях по всему миру.

Именно поэтому астрономы не оставляют новые объекты для личного наблюдения, а рассылают информацию всем подписавшимся на ее получение. В случае, если объект оказывается сверхновой типа Ia, что определяется по ее спектру, строится ее кривая блеска. По наблюдениям сверхновых типа Ia на близких расстояниях выяснилось, что светимость в максимуме все-таки немного меняется и для повышения точности следует ввести небольшую поправку, определяемую по форме кривой блеска. Именно светимость в максимуме и определяют при наблюдениях вспышек сверхновых. Кроме того, наблюдения спектра дают нам значение z-фактора.

Наблюдениями сверхновых типа Ia для задач космологии занимались сразу несколько групп. Вначале результаты их наблюдений вполне укладывались в теорию Фридмана, предсказывающую замедление расширения Вселенной. Как мы отмечали в разделе 2.6.1, это замедление описывается так называемым космологическим параметром замедления q, который всегда положителен в моделях Фридмана. Но все изменилось после того, как в 1998 г. вначале группа Адама Рисса, а затем группа Саула Перлмуттера объявили, что по данным их наблюдений Вселенная расширяется с ускорением и параметр замедления отрицателен. Соответствующие статьи были опубликованы в 1998 и 1999 гг. Это открытие, перевернувшее космологию, стало возможным благодаря повышению точности за счет увеличения выборки и введения описанной выше поправки. Кроме того, стало ясно, что до какого-то момента скорость разбегания галактик уменьшалась, достигла минимального значения, а затем стала увеличиваться. Это произошло при z ~ 0,645 или около 6,2×109 лет назад. Это является убедительным доказательством существования космологической постоянной или чего-то похожего на нее, что в настоящее время называется темной энергией.

Попутно это открытие решило еще одну проблему. Дело в том, что оценки возраста Вселенной, полученные из модели Фридмана, были меньше возраста самых старых из наблюдаемых звезд, что, конечно же, абсурдно. Если же Вселенная в течение какого-то времени расширяется с ускорением, то эта проблема снимается.

За это открытие Саул Перлмуттер, Адам Рисс и Брайан Шмидт получили Нобелевскую премию по физике 2011 г. Приведем некоторые подробности этого открытия на примере работы группы Перлмуттера. Они измерили параметры 42 сверхновых типа Ia с z-факторами от 0,17 до 0,83, из которых только 2 сверхновые имели z < 0,3, а для калибровки использовали выборку из 18 сверхновых с z-факторами от 0,02 до 0,10. Кроме того, они рассматривали случай, когда вместо космологической постоянной действует темная энергия с уравнением состояния (2.33), и пришли к выводу, что этот вариант не обеспечивает лучшего согласия с наблюдательными данными.

Немного позже космологи получили и возможность использовать что-то похожее на стандартную линейку. В ряде работ это называется барионными акустическими колебаниями (сокращенно BAO – baryon acoustic oscillations). В других работах пишут о кластеризации (скучивании) галактик или о крупномасштабной структуре. Попробуем объяснить простыми словами основную идею этого непростого явления. Как мы уже писали, в ранней Вселенной возникли и росли флуктуации плотности. При этом к областям повышенной плотности стекалось вещество из окружающих слоев. Темная материя спокойно падала на эту область, а обычной материи препятствовало возрастающее давление. В результате вокруг этой области появлялась волна плотности, распространяющаяся наружу со скоростью c/√3 (это значение было получено Яковом Зельдовичем). За время до рекомбинации волна достигла вполне определенного радиуса. После рекомбинации Вселенная стала прозрачна для излучения и излучение перестало быть «вмороженным» в материю. Условия роста флуктуаций изменились. Из них стала формироваться крупномасштабная структура Вселенной, в частности области образования галактик. Галактика, образовавшаяся в центре этой области, имеет наибольшее число соседей на расстоянии, равном радиусу этой волны. В настоящее время с учетом расширения Вселенной это расстояние близко к 150 Мпк. Таким образом, вероятность того, что две галактики будут находиться на расстоянии 150 Мпк, будет несколько выше, чем при случайном распределении.

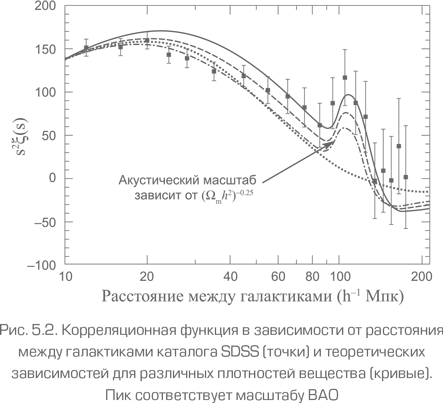
Этот эффект наблюдается во всех достаточно больших каталогах галактик, в частности на Слоуновском цифровом обзоре неба (Sloan Digital Sky Survey – SDSS). На рис. 5.2 показана корреляционная функция зависимости от расстояния между галактиками, показывающая отличие числа галактик на данном расстоянии от случайного. Основной особенностью этого графика является пик, соответствующий тому самому расстоянию около 150 Мпк. Параметры этого пика зависят от космологических параметров и позволяют наложить на них ограничения.

Третий способ получить ограничения на космологические параметры не требует наличия стандартных объектов. Это форма спектра мощности реликтового излучения, изображенного на рис. 3.2, т. е. распределение флуктуаций по гармоникам. Существуют достаточно сложные методы расчета формы этой кривой, в которых в качестве входных параметров задается ряд космологических параметров. Кроме плотностей разных компонентов ΩΛ, Ωm и Ωb задаются также параметр, характеризующий форму спектра флуктуаций, количество сортов нейтрино и другие параметры. Полученная форма сравнивается с наблюдаемой, и выбираются оптимальные значения параметров. В частности, форма кривой сильно зависит от значения Ωb. Некоторые из этих параметров получают непосредственно, например ΩΛ. Некоторые из них получают в комбинации, например Ωmh2 и Ωbh2. Однако следует отметить, что отношение Ωb/Ωm не зависит от h.

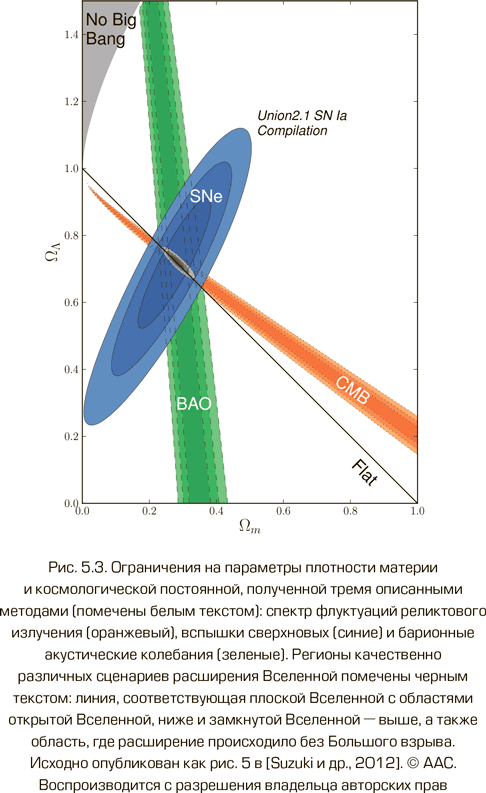
На рис. 5.3 изображены совместные ограничения (градации серого цвета) на Ωm и ΩΛ, полученные тремя описанными методами (с надписями белым цветом): спектр флуктуаций реликтового излучения (оранжевый), вспышки сверхновых (синий) и барионные акустические колебания (зеленый). Как видно, доверительные области пересекаются, образуя сравнительно небольшую область значений этих параметров, которые вписываются во все эти данные. Ограничения, полученные по слабому гравитационному линзированию, тоже включают эту область. Таким образом, ограничения, полученные из совершенно разных методов, пересекаются в одной области.

На том же рисунке указаны границы областей, соответствующих качественно разным физическим сценариям расширения Вселенной (отмечены черным цветом): линия, соответствующая плоской Вселенной, с областью открытой Вселенной ниже и замкнутой Вселенной выше, а также области, где расширение происходило без Большого взрыва. По тому, куда попала область совместных ограничений, мы можем сделать определенные выводы о прошлом и будущем Вселенной. При этом предсказания делаются в рамках стандартной на сегодняшний день ΛCDM-модели. Серая область в левом верхнем углу графика соответствует Вселенной, расширявшейся вечно без Большого взрыва. Ниже расположена область, в которой Вселенная имела начало, т. е. Большой взрыв, но будет расширяться вечно. Еще ниже находится область, в которой Вселенная рано или поздно коллапсирует. Понятно, что при Ωm ≤ 1 мы имеем дело с открытой или плоской моделями, в которых Вселенная будет расширяться вечно. Но в присутствии космологической постоянной вечное расширение возможно и для закрытой космологической модели, если плотность не сильно превышает критическую. Дополнительное отталкивание предотвратит коллапс. Кроме того, диагональная линия разделяет области с различной пространственной кривизной Вселенной: положительная кривизна сверху, отрицательная – снизу. Легко видеть, что область совместных ограничений соответствует Вселенной, рожденной в результате Большого взрыва, которая будет расширяться вечно. Ее пространственная кривизна близка к нулю. Последний вывод основан главным образом на исследованиях анизотропии реликтового излучения.

Кроме описанных методов существует и ряд других, например Лайман-альфа лес и эффект Сюняева – Зельдовича, которые также подтверждают существование и свойства темной материи.