ГЛАВА ТРИНАДЦАТАЯ

ГДЕ ПЕРЕСЕКАЮТСЯ ЖЕЛЕЗНОДОРОЖНЫЕ РЕЛЬСЫ

Понятие полезности помогает объяснить одно загадочное явление, связанное с лотереей Cash WinFall. С одной стороны, когда игроки группы Джеральда Селби покупали большое количество лотерейных билетов, они использовали функцию Quic Pic, позволяя компьютерам лотереи выбирать числа в случайном порядке. С другой стороны, игроки группы Random Strategies выбирали числа сами. Это означало, что они должны были заполнять десятки тысяч карточек вручную, а затем по одному вставлять их в автомат в выбранном магазине — трудоемкое и невероятно скучное занятие.

Выигрышные номера выпадают совершенно случайно, а значит, все лотерейные билеты имеют одинаковую ожидаемую ценность: 100 тысяч билетов Селби, выбранных с помощью компьютеров, обеспечили бы такое же количество призовых денег, что и 100 тысяч билетов Харви и Лу, заполненных вручную. Согласно ожидаемой ценности, игроки Random Strategies выполняли большой объем трудной работы без какого бы то ни было вознаграждения. Зачем?

Рассмотрим следующий пример — более простой, но аналогичный по своей сути. Вы предпочли бы взять 50 тысяч долларов, или заключить пари 50 на 50 между потерей 100 тысяч долларов и получением 200 тысяч долларов? Ожидаемая ценность этого пари составляет:

(1/2) × (−100 000 долларов) + (1/2) × (200 000 долларов) = 50 000 долларов,

то есть столько же, сколько и наличных денег. На самом деле действительно есть основания, чтобы нейтрально относиться к обоим вариантам: если вы многократно заключали бы такие пари, то почти наверняка в половине случаев получали бы 200 тысяч долларов, а в другой половине — 100 тысяч долларов. Представьте себе, что выигрыши и проигрыши чередуются: после двух пари вы выиграли 200 тысяч долларов и проиграли 100 тысяч долларов, получив в итоге 100 тысяч долларов; после четырех пари эта сумма составила бы 200 тысяч долларов, после шести — 300 тысяч долларов и так далее. В среднем ваша прибыль составила бы 50 тысяч долларов на одно пари, как и в случае, если вы с самого начала выбрали бы безопасный путь.

Теперь советую вспомнить, что вы не персонаж задачи из учебника по экономике, но живой человек — человек, у которого нет на руках 100 тысяч долларов. Когда вы проиграете свою первую ставку, к вам обязательно заглянет букмекер (этакий огромный, злой, наголо бритый парень с накачанными мышцами) и потребует вернуть долг. А вы ему в ответ: «Вычисление ожидаемой ценности показывает, что я, по всей вероятности, смогу выплатить вам долг в долгосрочном периоде». Вы допускаете, что в силах произнести такое? Конечно, нет. Ваш математически убедительный аргумент не достигнет своей цели.

Следовательно, если вы обычный живой человек, вам следует взять 50 тысяч долларов.

Такие рассуждения хорошо объясняет теория полезности. Если я — корпорация с неограниченными финансовыми средствами, то потеря 100 тысяч долларов может выглядеть не слишком страшным событием, оно обойдется мне, скажем, в 100 ютилей, тогда как выигрыш 200 тысяч долларов принесет 200 ютилей. В таком случае зависимость между долларами и ютилями может носить линейный характер, и тогда ютиль — всего лишь другое название тысячи долларов.

Но если я — обычный живой человек со скромными сбережениями, то вычисления будут совсем другими. Выигрыш 200 тысяч долларов изменит мою жизнь в гораздо большей степени, чем жизнь корпорации, а значит, это событие может иметь для меня более высокую ценность — скажем, 400 ютилей. А вот проигрыш 100 тысяч долларов не просто опустошит мой банковский счет: мне придется выплачивать долг сердитому бритому качку. Речь уже не идет о просто плохом показателе в балансовой ведомости. Мы рискуем получить серьезные физические увечья, и этот риск мы можем оценить в 1000 ютилей. В таком случае ожидаемая полезность этого пари составляет:

(1/2) × (−1000) + (1/2) × (400) = −300

Отрицательная полезность данного пари означает, что данный вариант развития событий не просто хуже верных 50 тысяч долларов; он даже хуже того, если вы вообще ничего не делали бы. Равная 50% вероятность, что вы будете разорены, означает риск, который вы не можете себе позволить, во всяком случае без перспективы получения намного большего вознаграждения.

Я показал математический способ формального описания принципа, с которым вы уже знакомы: чем более вы богаты, тем больше вы позволяете себе рисковать. Такие пари, как в представленном выше примере, подобны рискованным инвестициям с положительным ожидаемым выигрышем: когда вы часто делаете такие капиталовложения, то в некоторых случаях неизбежны какие-то денежные потери, но в долгосрочной перспективе вы остаетесь с прибылью. Чтобы покрыть нерегулярные потери, богатый человек, имеющий достаточно большой резерв, продолжает инвестировать и становится еще богаче. Небогатые люди остаются там же, где и находились.

Рискованные инвестиции могут иметь смысл даже в случае, если у вас нет денег для покрытия потерь, но только при условии, что вы предусмотрели запасной план. Определенное действие на рынке может обеспечить возможность заработать 1 миллион долларов с вероятностью 99% и потерять 50 миллионов долларов с вероятностью 1%. Целесообразно ли совершать этот шаг? Он имеет положительную ожидаемую ценность, поэтому кажется хорошей стратегией. Также вы можете отказаться от риска нести такие большие убытки — главным образом потому, что настолько малые вероятности, как известно, трудно оценить довольно точно. Профи придумали для таких случаев меткую фразу: «Все равно что подбирать десятицентовики на пути парового катка». В большинстве случаев вы получаете не слишком много денег, но стоит поскользнуться — и каток вас раздавит.

Так что делать? Одна из стратегий сводится к тому, чтобы по полной использовать заемные средства — до тех пор пока не соберется вдоволь бумажных активов, — тогда вы делаете свой рискованный шаг, поставив на кон в сто раз больше денег. Теперь вы можете получать по 100 миллионов на каждую транзакцию — отлично! Что случится, если паровой каток вас все-таки настигнет? Вы потеряете 5 миллиардов. А может быть, и нет. Ведь сегодня, когда всё завязано друг на друге, мировая экономика представляет собой большой разваливающийся дом на дереве, который держится исключительно за счет ржавых гвоздей и веревки. Серьезное крушение в одном месте моментально создаст угрозу полного обвала нашей хибары. Однако Федеральная резервная система США решительно настроена на то, чтобы не допустить никакого краха. Как говорится, если вы потеряли миллион — это ваша проблема, а если пять миллиардов — проблема правительства.

Довольно циничная финансовая стратегия, но во многих случаях она срабатывает. В частности, она оправдала себя в 1990-е годы с хеджевым фондом Long-Term Capital Management — его истории посвящена замечательная книга Роджера Ловенстайна When Genius Failed («Когда гений терпит поражение»). Кроме того, эта стратегия оправдала себя с компаниями, выжившими и даже извлекшими для себя выгоду из финансового кризиса 2008 года. Сегодня, в отсутствие кардинальных перемен, которых пока нигде не видно, подобная финансовая политика снова станет востребованной.

Финансовые компании все-таки не люди, а вот большинство людей, даже богатых, не любят неопределенности. Богатый инвестор может охотно заключить пари 50 на 50 с ожидаемой ценностью 50 тысяч долларов, но скорее он предпочтет сразу взять 50 тысяч долларов. Для данного явления существует специальный термин — дисперсия, или мера рассеяния возможных последствий того или иного решения, а также вероятность крайних значений. Из всей совокупности сделок, имеющих одну и ту же ожидаемую денежную стоимость, большинство людей (особенно людей, у которых нет неограниченных ликвидных активов) отдают предпочтение вариантам с более низкой дисперсией. Именно поэтому многие вкладывают деньги в муниципальные облигации, хотя акции обеспечивают более высокую рентабельность инвестиций в долгосрочной перспективе. Имея дело с облигациями, вы обязательно вернете свои деньги. Рискните инвестировать в акции с их более высокой дисперсией — вы, вероятно, добьетесь большего, но в то же время все может закончиться и гораздо хуже.

Как бы мы ни обозначали происходящее, но борьба с дисперсией представляет собой основную задачу управления деньгами. Именно из-за дисперсии пенсионные фонды диверсифицируют свои инвестиции. Если все ваши деньги вложены в акции нефтяных и газовых компаний, одно большое потрясение в энергетическом секторе может сжечь весь ваш портфель. Вам необходимо раскладывать яйца в разные корзины, во много разных корзин. Когда вы вкладываете все свои сбережения в крупный индексный фонд, распределяющий инвестиции по всем секторам экономики, вы придерживаетесь именно этого принципа. Данной стратегии посвящены некоторые работы с математическом уклоном, в которых можно найти практические советы по финансовым вопросам, например книга Бертона Малкиела A Random Walk Down Wall Street («Случайная прогулка по Уолл-стрит») — стратегия унылая, но действенная. Если вас волнует порядок выхода на пенсию, то…

Акции, как минимум в долгосрочной перспективе, в среднем становятся более ценными; другими словами, инвестирование в фондовый рынок — это шаг, имеющий положительную ожидаемую ценность. В случае отрицательной ожидаемой ценности совсем иные расчеты: люди так же не любят верные проигрыши, как любят верные выигрыши. Следовательно, вас интересует более высокая, а не более низкая дисперсия. Вряд ли вы увидите в казино, как люди подходят к колесу рулетки и с важным видом ставят по одной фишке на каждое число — слишком неоправданный и чрезмерно сложный способ отдавать крупье свои фишки.

Какое отношение все сказанное имеет к лотерее Cash WinFall? Как мы уже говорили, ожидаемая ценность 100 тысяч лотерейных билетов одна и та же, какие бы билеты вы ни покупали. Однако дисперсия — совсем другое дело. Предположим, я приму решение сделать большую ставку в этой игре, но поступлю другим способом: куплю 100 тысяч копий одного и того же лотерейного билета.

Если случится так, что во время розыгрыша лотереи в этом билете совпадут четыре цифры из шести, тогда я стану счастливым обладателем 100 тысяч билетов, выигравших в категории «Четыре совпадения». По существу, мне достанется весь призовой фонд в размере 1,4 миллиона долларов, то есть очень большой доход в размере 600%. Но если мой набор цифр проиграет, я потеряю все свои 200 тысяч долларов. Это пари с высокой дисперсией, когда существует большая вероятность крупного выигрыша и небольшая вероятность еще большего проигрыша.

Таким образом, «не ставить все деньги на одно число» — весьма правильный совет, гораздо лучше вести игру в более широком диапазоне. Но разве не этим занималась группа Селби, когда использовала при покупке лотерейных билетов функцию Quic Pic, которая обеспечивает случайный выбор чисел?

Не совсем. Хотя Селби не ставил все свои деньги на один билет, он все-таки действительно покупал много билетов с одинаковыми числами. На первый взгляд это кажется странным. В период самой активной игры группа Селби покупала по 300 тысяч лотерейных билетов на один розыгрыш, предоставляя компьютеру в случайном порядке выбирать числа из 10 миллионов вариантов. Следовательно, объем покупок Селби составлял всего 3% от возможных билетов. В таком случае какова вероятность того, что он покупал два билета с одинаковыми числами?

На самом деле эта вероятность довольно высокая. Вспомним старую шутку: соберите гостей на вечеринку, и выяснится, что двое из них родились в один день. Но это должна быть большая вечеринка — скажем, человек на тридцать. Тридцать дней рождения из 365 вариантов — это не слишком много, а значит, вряд ли два из этих дней рождения выпадут на одну дату. Однако речь идет не о количестве людей, а о количестве пар. Нетрудно вычислить, что есть 435 пар людей, а также что каждая пара может иметь общий день рождения с вероятностью 1 из 365. Следовательно, на такой вечеринке вы вполне можете встретить пару людей (а возможно, даже две пары), родившихся в один день. На самом деле вероятность, что из тридцати человек двое родились в один день, равна немногим более 70% — довольно большое значение. А если вы покупаете 300 тысяч лотерейных билетов, выбранных случайным образом из 10 миллионов вариантов, вероятность покупки двух билетов с одинаковыми числами настолько близка к 1, что я предпочитаю не вычислять, сколько еще девяток мне нужно после 99,9%, а просто использую слово наверняка, чтобы получить точное значение вероятности.

Однако проблема не только в дублировании лотерейных билетов. Как и всегда, чтобы нарисовать соответствующую картину, легче будет понять, что происходит с математическими расчетами, если взять достаточно малые величины. Поэтому давайте устроим розыгрыш лотереи с участием всего семи шаров, из которых штат выбирает три шара в качестве комбинации, за которую выплачивается джекпот. Существует всего тридцать пять таких комбинаций, соответствующих тридцати пяти различным способам, которыми можно выбрать три числа из множества 1, 2, 3, 4, 5, 6, 7. Вот эти комбинации в порядке возрастания чисел:

123 124 125 126 127

134 135 136 137

145 146 147

156 157

167

234 235 236 237

245 246 247

256 257

267

345 346 347

356 357

367

456 457

467

567

Предположим, Джеральд Селби идет в магазин и покупает семь лотерейных билетов с числами, выбранными случайным образом с помощью функции Quic Pic. (Лотерею с такой структурой называют иногда трансильванской лотереей, хотя я не нашел свидетельств, что в нее когда-либо играли в Трансильвании или чтобы ею баловались вампиры.)

Угадать два числа из трех довольно легко, поэтому я больше не буду говорить «два из трех»; давайте просто назовем получающий меньший выигрыш билет двойкой. Например, если в розыгрыше джекпота выпадают номера 1, 4 и 7, четыре билета с одним числом 1, одним числом 4 и каким-то количеством чисел, отличающихся от числа 7, — это двойки. Кроме этих четырех билетов есть еще четыре билета, в которых угаданы числа 1–7, а также еще четыре с числами 4–7. Таким образом, двенадцать билетов из тридцати пяти, то есть более трети возможных билетов, — это двойки. А значит, среди семи билетов Джеральда Селби есть минимум пара двоек. Выполнив необходимые расчеты, можно получить более точные значения вероятности того, что у Селби будет то или иное количество двоек.

Вероятность полного отсутствия двоек составляет 5,3%.

Вероятность одной двойки составляет 19,3%.

Вероятность двух двоек составляет 30,3%.

Вероятность трех двоек составляет 26,3%.

Вероятность четырех двоек составляет 13,7%.

Вероятность пяти двоек составляет 4,3%.

Вероятность шести двоек составляет 0,7%.

Вероятность семи двоек составляет 0,1%.

Таким образом, ожидаемое количество двоек равно:

5,3% × 0 + 19,3% × 1 + 30,3% × 2 + 26,3% × 3 + 13,7% × 4 + 4,3% × 5 + 0,7% × 6 + 0,1% × 7 = 2,4.

Однако в трансильванской версии стратегии Джеймса Харви функция Quic Pic не используется: он заполняет все семь билетов вручную. Вот что получается в таком случае:

124

135

167

257

347

236

456

Предположим, в розыгрыше лотереи выпадают числа 1, 3 и 7. Это значит, что у Харви три двойки — 135, 167 и 347. А что если выпадут номера 3, 5 и 6? Тогда у Харви снова было бы три двойки — 135, 236 и 456. Продолжив перебирать возможные комбинации, вы вскоре увидите, что у всех вариантов Харви есть одно особое свойство: он выиграет либо джекпот, либо в точности три двойки. Вероятность того, что среди билетов Харви есть билет, выигравший джекпот, — 7 из 35, или 20%. Таким образом, вероятность двоек среди лотерейных билетов Харви такова:

вероятность полного отсутствия двоек составляет 20%;

вероятность трех двоек составляет 80%.

Следовательно, ожидаемое количество двоек в случае Харви равно:

20% × 0 + 80% × 3 = 2,4.

Другими словами, это то же самое значение, как и должно быть. Однако во втором случае дисперсия гораздо меньше, а значит, у Харви почти нет сомнений в том, сколько двоек он получит. Что делает портфель Харви гораздо более привлекательным для потенциальных членов его группы. Обратите особое внимание на следующее: каждый раз, когда у Харви нет трех двоек, он выигрывает джекпот. Следовательно, стратегия Харви гарантирует довольно большой минимальный выигрыш — выигрыш, который вряд ли получится у игроков, подобных Селби, выбирающих числа с помощью функции Quic Pic. Самостоятельно выбирая числа, вы можете устранить риск и в то же время получить вознаграждение — если только выберете правильные числа.

Как это сделать? Вопрос на миллион долларов — в данном случае в буквальном смысле слова.

Рассмотрим первый способ, когда можно просто попросить свой компьютер сделать это. Харви и члены его команды были студентами MIT, скорее всего, способными написать несколько дюжин строк кода еще до утренней чашки кофе. Почему просто не придумать программу, которая перебрала бы все комбинации 300 тысяч билетов лотереи WinFall в поисках стратегии с самой низкой дисперсией?

Написать такую программу было бы не трудно. Есть только одна небольшая проблема: всю материю и энергию во Вселенной постигла бы тепловая смерть, прежде чем ваша программа обработала бы первый крохотный фрагмент мельчайшего клочка данных, которые вы пытаетесь проанализировать. Для современного компьютера 300 тысяч — не слишком большое число. Однако объекты, которые должна перебрать предложенная программа, — не 300 тысяч билетов, а возможные наборы 300 тысяч билетов, которые предстоит купить из 10 миллионов возможных билетов лотереи Cash WinFall. Сколько всего таких наборов? Больше 300 тысяч. Больше количества субатомных частиц, существующих или когда-либо существовавших во Вселенной. Намного больше. Скорее всего, вы даже не слышали о настолько большом числе, как количество способов выбора ваших 300 тысяч билетов.

Здесь мы столкнулись с ужасающим феноменом, который программисты называют «комбинаторный взрыв». Говоря простым языком, очень простые операции могут превратить приемлемо большое количество вариантов в абсолютно не поддающееся обработке количество. Если вы хотите узнать, какой из пятидесяти штатов является самым выгодным местом для размещения вашего бизнеса, определить это не составит труда — довольно просто сопоставить пятьдесят разных объектов. Но если вам необходимо определить, какой маршрут передвижения через все пятьдесят штатов наиболее эффективен (так называемая задача коммивояжера), произойдет комбинаторный взрыв, и вы столкнетесь с трудностями совсем другого порядка: вам предстоит делать выбор из 30 вигинтиллионов маршрутов. В более знакомых терминах это 30 тысяч триллионов триллионов триллионов триллионов.

Следовательно, чтобы снизить уровень дисперсии, нам лучше найти другой способ выбирать лотерейные билеты. Поверите ли вы мне, если я скажу, что все сводится к планиметрии?

ГДЕ ЖЕЛЕЗНОДОРОЖНЫЕ РЕЛЬСЫ ПЕРЕСЕКАЮТСЯ…

Параллельные линии не пересекаются. Это и делает их параллельными.

Но иногда параллельные линии выглядят так, будто пересекаются. Вспомните о паре железнодорожных рельсов в пустынной местности, которые как будто сходятся в одной точке, по мере того как ваш взгляд перемещается по ним все ближе к горизонту. (По моему мнению, мысленный образ встречающихся друг с другом двух рельсов станет еще ярче, если включить музыку в стиле кантри.) Здесь имеет место феномен перспективы; когда вы пытаетесь отобразить трехмерный мир в двумерном поле зрения, чем-то придется пожертвовать.

Первыми, кто разобрался с этим явлением, оказались люди, которым было необходимо постичь: во-первых, суть объектов; во-вторых, как они выглядят; в-третьих, разницу между реальным объектом и его визуальным образом. Речь идет о художниках. Когда в начале эпохи итальянского Возрождения художники поняли феномен перспективы, визуальное представление изменилось навсегда: с этого момента картины европейских художников перестали напоминать рисунки ваших детей на дверце холодильника (в том случае, если ваши дети рисуют в основном распятого на кресте Иисуса) и стали похожими на то, что на них изображено.

Вопрос, как именно флорентийские художники, например Филиппо Брунеллески, пришли к пониманию современной теории перспективы, стал предметом множества дискуссий среди искусствоведов. Мы не будем вдаваться в детали их споров. Но мы наверняка знаем: этот прорыв стал возможен благодаря соединению эстетических соображений с новыми идеями в области математики и оптики. Отправной точкой стало понимание, что изображения, которые мы видим, формируются лучами света, отражающимися от объектов и попадающими в наши глаза. Современному человеку это кажется очевидным, но в те времена, поверьте, было далеко не так. Многие ученые древности — самый известный из них Платон — утверждали, что одним из элементов зрительного восприятия должен быть некий огонь, который испускают глаза. Эта точка зрения восходит как минимум к Алкмеону Кротонскому; считается, что на его мировоззрение повлияло учение Пифагора и пифагорейской школы (о взглядах пифагорейцев шла речь во ). Алкмеон утверждал, что глаза должны испускать огонь, иначе из какого еще источника могут появляться фосфены — звезды, которые вы видите, когда закрываете глаза и надавливаете пальцем на глазное яблоко? Теорию зрительного восприятия посредством отраженных лучей разработал на довольно подробном уровне каирский математик XI столетия Абу Али аль-Хасан ибн аль-Хасан ибн аль-Хайсам аль-Басри (но давайте называть его Альхазеном, как делают большинство западных авторов). Трактат Альхазена об оптике Kitab al-Manazir («Книга оптики») был переведен на латинский язык и с воодушевлением принят философами и художниками, искавшими более систематическую трактовку связи между взглядом и тем, на что он направлен. Основная мысль сводится к следующему: точка Р на вашем холсте представляет прямую линию в трехмерном пространстве. Благодаря Евклиду мы знаем, что существует только одна прямая линия, которая проходит между двумя заданными точками. В данном случае это линия, которая проходит через точку Р и ваш глаз. Любой объект, расположенный на этой линии, необходимо рисовать в точке Р.

А теперь представьте себя Филиппом Брунеллески, стоящим в степи; перед вами холст на мольберте, и вы рисуете железнодорожный путь. Этот путь состоит из двух рельсов, которые мы обозначим R₁ и R₂. Каждый из этих рельсов, нарисованный на холсте, должен представлять собой прямую линию. А подобно тому как точка на холсте соответствует прямой в пространстве, прямая линия на холсте соответствует плоскости. Плоскость P₁, соответствующая рельсу R₁, — это и есть та плоскость, которая образована прямыми, соединяющими каждую точку на этом рельсе с вашим глазом. Точно так же плоскость P₂, соответствующая рельсу R₂, — это плоскость, на которой находится ваш глаз и рельс R₂. Пересечение каждой из этих плоскостей с холстом представляет собой прямую линию; обозначим эти прямые L₁ и L₂.

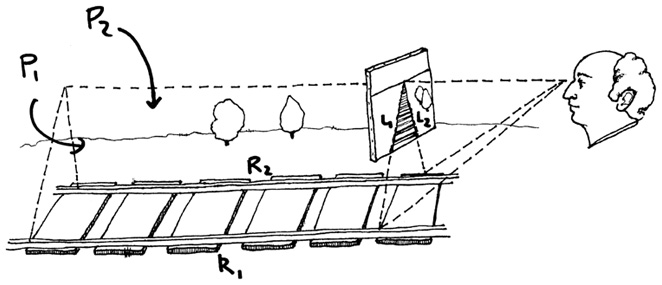
Эти два рельса параллельны друг другу. Однако две плоскости не параллельны. Как они могут быть параллельными? Они ведь пересекаются в вашем глазу, а параллельные плоскости не пересекаются. Плоскости, которые не являются параллельными, должны иметь пересечение в виде прямой линии. В данном случае это горизонтальная линия, которая исходит из вашего глаза и проходит дальше параллельно рельсам. Эта линия, будучи горизонтальной, не пересекается со степью: она стремится к горизонту, не касаясь поверхности земли. Однако (и в этом весь смысл происходящего) она пересекается с холстом в точке V. Поскольку точка V находится на плоскости R₁, она должна быть на линии L₁, вдоль которой рельс R₁ пересекается с холстом. А поскольку точка V находится также на плоскости R₂, она должна быть на линии L₂. Другими словами, V — это точка на холсте, в которой пересекаются нарисованные рельсы. На самом деле любой путь в степи, пролегающий параллельно рельсам, будет выглядеть на холсте как линия, которая проходит через точку V. Точка V — так называемая точка схода, то есть точка, через которую проходят все нарисованные линии, параллельные рельсам. В действительности каждая пара параллельных рельсов образует определенную точку схода на холсте, а положение этой точки зависит от направления параллельных линий. (Исключение составляют только пары прямых линий, параллельных самому холсту, как шпалы между рельсами — на картине они по-прежнему выглядят как параллельные.)

Концептуальный сдвиг, который совершил Филиппо Брунеллески, лежит в основе того, что математики называют проективной геометрией. Вместо точек на местности мы анализируем прямые линии, проходящие через наш глаз. На первый взгляд различие может показаться сугубо семантическим: каждая точка на поверхности земли определяет одну и только одну линию между этой точкой и нашим глазом, так не все ли равно, о чем мы думаем — о точке или о прямой? Разница вот в чем: количество линий, которые проходят через наш глаз, больше количества точек на поверхности, поскольку среди них есть еще и горизонтальные линии, вообще не пересекающиеся с поверхностью земли. Эти прямые соответствуют точкам схода на нашем холсте, то есть тем местам, в которых пересекаются рельсы. Вы можете представить такую линию как точку на поверхности, которая расположена «бесконечно далеко» в направлении рельсов. Математики обычно называют их бесконечно удаленными точками. Если взять плоскость, известную Евклиду, и изобразить на ней бесконечно удаленные точки, получится проективная плоскость. Вот рисунок такой плоскости.

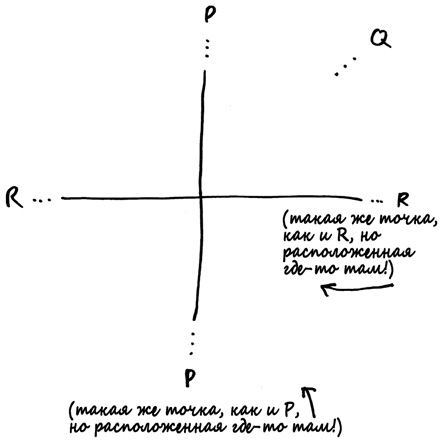
Большая часть проективной плоскости выглядит точно так же, как и обычная плоскость, к которой вы привыкли. Однако на проективной плоскости больше точек: на ней есть так называемые бесконечно удаленные точки — по одной на каждое возможное направление, в котором прямая может быть ориентирована на плоскости. Вы должны представлять себе точку Р, соответствующую вертикальному направлению, как расположенную бесконечно высоко по вертикальной оси, но также и как расположенную бесконечно низко по вертикальной оси. На проективной плоскости два конца оси Y сходятся в бесконечно удаленной точке, поэтому данная ось на самом деле представляет собой не прямую линию, а окружность. Аналогичным образом Q — это точка, расположенная бесконечно далеко на северо-восток (или на юго-запад), а R — точка, которая находится в конце горизонтальной оси. Или, скорее, на обоих концах. Если вы будете перемещаться бесконечно далеко вправо, до тех пор пока не окажетесь в точке R, а затем продолжите идти дальше, то обнаружите, что по-прежнему двигаетесь вправо, но теперь возвращаетесь в центр от левого края рисунка.

Ситуация «отправился по одному пути, вернулся по другому» поразила молодого Уинстона Черчилля, который дал яркое описание одного математического откровения, произошедшего в его жизни:

Однажды я прочувствовал математику, словно обозрел ее всю, все ее глубины раскрылись передо мной, вся ее бездонность. Подобно тому как многие наблюдают за прохождением Венеры или шествием лорда-мэра, я наблюдал за полетом величины через бесконечность и сменой ее знака с плюса на минус. Я понял, почему это происходит и как один шаг влечет за собой все другие. Похоже на политику. Но озарение пришло после плотного ужина — и мне было не до него!

По существу, точка R — не просто конечная точка горизонтальной оси, а конечная точка любой горизонтальной линии. Если есть две линии и они обе горизонтальные, значит, это параллельные линии. Тем не менее в проективной геометрии они пересекаются в бесконечно удаленной точке. Дэвиду Фостеру Уоллесу в 1996 году в одном из интервью задали вопрос о концовке романа Infinite Jest («Бесконечная шутка»), который многие считали незавершенным. Журналист поинтересовался у Уоллеса, не уклоняется ли тот от написания заключительной части романа, потому что ему «надоело его писать». Уоллес довольно раздраженно ответил:

Концовка есть, как мне кажется. Считается, что определенные типы параллельных линий начинают сходиться таким образом, что читатель может спроецировать «конец» куда-то за пределы правильной системы координат. Если вы не увидели такого схождения или проекции, значит, книга для вас потеряна.

*   *   *

У проективной плоскости есть недостаток: ее трудно нарисовать. Но есть у нее и преимущество, делающее правила геометрии более согласованными. На евклидовой плоскости две различные точки определяют одну прямую, а две различные прямые определяют одну точку пересечения, если только они не параллельные — в таком случае они вообще не пересекаются. В математике мы любим правила, но не любим исключений. С проективной плоскостью вам не придется делать никаких исключений в правиле, говорящем, что две прямые пересекаются в одной точке, поскольку параллельные прямые также пересекаются. Например, любые две вертикальные линии пересекаются в точке Р, а две линии, указывающие с северо-восточного направления в юго-западном, пересекаются в точке Q. Две точки определяют одну линию, две линии пересекаются в одной точке, вот и все. Здесь имеет место идеальная симметрия, простота и изысканность, не свойственные классической планиметрии. Совсем не случайно, что проективная геометрия возникла естественным образом в результате попыток решить практическую задачу отображения трехмерного мира на плоском холсте. Как раз за разом показывает история науки, математическая элегантность и практическая полезность идут рука об руку. Порой ученые открывают теорию и предоставляют математикам искать объяснение ее элегантности; в других случаях математики разрабатывают элегантную теорию и оставляют ученым искать области ее применения.

Реалистическая живопись — та область деятельности, в которой применяется проективная плоскость. Еще одна такая область — выбор лотерейных номеров.

МИНИАТЮРНАЯ ГЕОМЕТРИЯ

В основе геометрии проективной плоскости лежат две аксиомы.

Каждая пара точек лежит ровно на одной общей прямой.

Каждая пара прямых линий содержит ровно одну общую точку.

Когда математики обнаружили одну разновидность геометрии, удовлетворявшую этим двум идеально согласованным аксиомам, вполне естественно было задать вопрос, существуют ли другие типы геометрии. Оказывается, есть много таких геометрий, одни большие, а другие маленькие. Самая крохотная из них называется «плоскость Фано», по имени ее создателя Джино Фано, который был одним из первых математиков конца XIX столетия, всерьез воспринявших идею конечных геометрий. Вот как выглядит плоскость Фано.

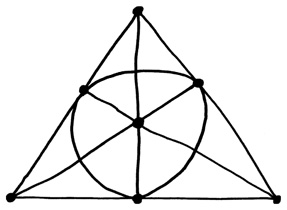
Действительно совсем небольшая геометрическая система, состоящая всего из семи точек! В качестве «прямых» в ней выступают линии, показанные на рисунке; линии также маленькие, поскольку на каждой из них всего по три точки. Существует семь таких линий, шесть из которых выглядят как прямые, а седьмая похожа на окружность. И все-таки эта так называемая геометрия, и без того экзотическая, удовлетворяет и первой и второй аксиомам точно так же, как плоскость Брунеллески.

Фано придерживался современного подхода, достойного восхищения: у него была, говоря словами Харди, «привычка определения», поскольку он избегал вопроса, не имеющего ответа, а именно: «Что такое геометрия?» Вместо этого он спрашивал: «Какой феномен ведет себя подобно геометрии?» Вот свидетельство самого Фано:

A base del nostro studio noi mettiamo una varietà qualsiasi di enti di qualunque natura; enti che chiameremo, per brevità, punti indipendentemente però, ben inteso, dalla loro stessa natura.

А это перевод:

В качестве основы нашего исследования мы исходим из предположения, что существует произвольная совокупность объектов произвольной природы — объектов, которые мы для краткости называем точками, но это не имеет отношения к их природе.

Для Фано и его интеллектуальных преемников не имеет значения, «как выглядит» прямая — похожа ли она на линию, на окружность, на крякву или на что угодно. Важно лишь то, что прямые линии подчиняются законам прямых линий — законам, установленным Евклидом и его преемниками. Если это ходит как геометрия и крякает как геометрия, значит, будем называть это геометрией. Существует точка зрения, согласно которой такой шаг создает разрыв между математикой и реальностью, чему необходимо противостоять. Мнение чрезмерно консервативное. Смелая идея, что мы можем размышлять в геометрических категориях о системах, не похожих на евклидово пространство, и называть эти системы геометриями — причем говорить об этом с высоко поднятой головой, — сыграла решающую роль в осмыслении релятивизма геометрии пространственно-временного континуума, в котором мы живем. В настоящее время мы используем обобщенные геометрические идеи для построения карты интернет-пространства, которое представляет собой нечто весьма далекое от того, что мог представить Евклид. Это один из аспектов красоты математики: мы разрабатываем совокупность идей, и если они верны, то они верны, даже если их применение выходит далеко за рамки контекста, в котором они изначально были задуманы.

Возьмем в качестве иллюстрации такой пример. На рисунке снова изображена плоскость Фано, но точки на ней обозначены числами от 1 до 7.

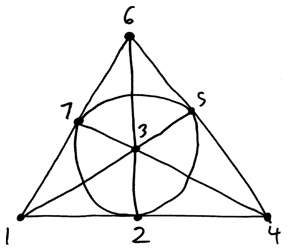
Выглядит знакомо? Если составить список этих семи линий, обозначив их совокупностью трех точек, которые расположены на каждой из них, получится следующее:

124

135

167

257

347

236

456

Это не что иное, как совокупность семи лотерейных билетов, о которых мы говорили выше, — совокупность, в которой каждая пара чисел выпадает только один раз, гарантируя минимальный выигрыш. В тот момент такое свойство казалось впечатляющим и загадочным. Как может кто бы то ни было сформировать столь идеально упорядоченное множество лотерейных билетов?

Ну вот, только что с моей помощью ларчик открылся и продемонстрировал суть фокуса: все дело в геометрии. Каждая пара чисел появляется ровно в одном билете, поскольку каждая пара точек лежит ровно на одной прямой. Это всего лишь Евклид, правда, говорим мы теперь о точках и линиях, и вряд ли Евклид их узнал бы.

ПРОШУ ПРОЩЕНИЯ, ВЫ СКАЗАЛИ «BOFAB»?

Плоскость Фано подсказывает нам, как без всякого риска играть в трансильванскую лотерею из семи чисел, но как насчет лотереи штата Массачусетс? Существует множество конечных геометрий с количеством точек, большим семи, но ни одна из них, к сожалению, не отвечает полностью требованиям лотереи Cash WinFall. В этом случае необходимо нечто более универсальное. Решение проблемы проистекает не непосредственно из живописи эпохи Возрождения или евклидовой геометрии, а из еще одного неожиданного источника — теории цифровой обработки сигналов.

Предположим, мне нужно отправить на спутник важное сообщение, например, «Включить правый двигатель». Спутники не разговаривают на человеческом языке, поэтому на самом деле я отправляю последовательность единиц и нулей — то, что программисты называют битами:

1110101…

Сообщение кажется четким и недвусмысленным. Однако в реальной жизни в каналах связи бывают помехи. Может быть, космический луч попадает в спутник в тот момент, когда спутник принимает ваше сообщение, и искажает один бит информации, поэтому в итоге получается такое сообщение:

1010101…

На первый взгляд может показаться, что это сообщение не очень отличается от предыдущего, но, если изменение одного бита информации приведет к замене команды «включить правый двигатель» на команду «включить левый двигатель», у спутника могут возникнуть серьезные проблемы.

Спутники стоят очень дорого, а значит, лучше избегать подобных проблемных ситуаций. Когда вы пытаетесь поговорить с приятелем на бурной вечеринке, то имеете возможность повторить сказанное, и ваши слова не утонут в общем шуме. Данный способ применим и в нашем случае: в исходном сообщении можно продублировать каждый бит, отправив 00 вместо 0 и 11 вместо 1:

11 11 11 00 11 00 11…

Теперь, когда космический луч выбьет второй бит сообщения, спутник увидит такую последовательность:

10 11 11 00 11 00 11…

Спутник знает, что каждый сегмент из двух бит должен представлять собой либо 00, либо 11, а значит, сигнал «10» — признак того, что что-то не в порядке. Но что именно? Спутнику трудно разобраться с этим, поскольку он не знает, в каком именно месте помеха исказила сигнал, не существует способа определить, как выглядело исходное сообщение — 00 или 11.

Но и эту проблему можно исправить, повторив каждый бит три раза вместо двух:

111 111 111 000 111 000 111…

Предположим, сообщение приходит в искаженном виде:

101 111 111 000 111 000 111…

Теперь спутник готов к этому. Он знает, что первый сегмент из трех бит должен представлять собой 000 или 111, а значит, присутствие 101 означает, что что-то пошло не так. Но, если в исходном сообщении была бы последовательность 000, это означало бы, что искажены два бита, расположенные в непосредственной близости друг от друга, — маловероятное событие, учитывая редкость космических лучей, искажающих сообщения. Следовательно, у спутника есть все основания применить принцип большинства: если два из трех бит содержат 1, велика вероятность, что в исходном сообщении была последовательность 111.

Вы только что увидели пример кода с исправлением ошибок — протокол обмена данными, позволяющий получателю устранять ошибки в искаженном сигнале. Эта идея, как практически и все остальное в теории информации, сформулирована в вышедшей в 1948 году и ставшей сразу классической работе Клода Шеннона Mathematical Theory of Communication («Математическая теория связи»).

Математическая теория коммуникации! Звучит несколько претенциозно, не так ли? Разве коммуникация — не сугубо человеческий вид деятельности, который нельзя свести к холодным цифрам и формулам?

Я хочу, чтобы вы понимали: я от всей души поддерживаю и настоятельно рекомендую демонстрировать жесткий скептицизм по отношению к любым заявлениям, что ту или иную сущность можно объяснить, или укротить, или полностью понять математическими средствами.

Тем не менее история математики представляет собой историю агрессивной территориальной экспансии, поскольку математические методы становятся все более всеобъемлющими и богатыми, а математики находят способы изучать вопросы, которые раньше считались находящимися вне их области знаний. В наше время словосочетание «математическая теория вероятностей» выглядит вполне обычным, но когда-то могло показаться большим перегибом: математика занималась только изучением определенного и истинного, а не случайного и возможного! Ситуация изменилась, когда Паскаль, Бернулли и другие математики открыли математические законы, описывающие действие случая. Математическая теория бесконечности? До работы Георга Кантора в XIX столетии изучение бесконечности было не столько наукой, сколько теологией; сейчас мы понимаем теорию Кантора о множественности бесконечностей, каждая из которых бесконечно больше предыдущей, настолько полно, что преподаем эту тему первокурсникам, изучающим математику. (По правде сказать, она действительно поражает их воображение.)

Формальные математические модели не охватывают все детали того феномена, который описывают, они и не должны этого делать. Например, существуют вопросы о случайности — на них теория вероятностей не дает ответа. В понимании некоторых людей проблемы, остающиеся вне досягаемости математики, представляют собой самые интересные вопросы. Но в наши дни было бы ошибкой размышлять о случае, не опираясь на теорию вероятностей. Если не верите мне, спросите Джеймса Харви. Или, что еще лучше, спросите об этом у людей, чьи деньги он выиграл.

Появится ли когда-либо математическая теория сознания? Общества? Эстетики? Кто-то наверняка пытается создать такие теории, но пока безуспешно. Заявления такого рода должно каждый раз подвергать сомнению, полагаясь на интуицию. Но также следует помнить, что в конечном счете они могут правильно интерпретировать некоторые вещи.

На первый взгляд код с исправлением ошибок не кажется революционным математическим методом. Ведь мы всегда повторяем сказанное, когда находимся в шумном месте, — и таким образом решаем проблему! Но у данного решения есть своя цена. Если вы будете повторять каждый бит информации три раза, для передачи сообщения понадобится в три раза больше времени. Вряд ли это послужит препятствием на громогласной вечеринке, но может стать настоящей проблемой, если вам необходимо, чтобы спутник включил правый двигатель в данную секунду. В своей работе, положившей начало теории информации, Шеннон описал негативный побочный эффект, с которым инженеры борются до сих пор: чем более устойчивым к помехам вы хотите сделать свой сигнал, тем медленнее будут передаваться биты. Присутствие шума ограничивает длину сообщения, которое ваш канал связи может безопасно передать за определенное количество времени. Шеннон обозначил этот предел термином пропускная способность канала. Подобно тому как труба пропускает только определенное количество воды, канал связи также передает только определенный объем информации.

Однако для исправления ошибок не обязательно сокращать пропускную способность канала связи, как того требует протокол «повторить три раза». Шеннон знал, что их можно исправить более эффективно, поскольку Ричард Хэмминг, его коллега по Bell Labs, уже понял, как решить данную проблему.

У Хэмминга, молодого ветерана Манхэттенского проекта, в Bell Labs был доступ к десятитонной релейной вычислительной машине Model V, однако уровень его допуска позволял ему работать с этой машиной только по выходным. Проблема заключалась в том, что любая механическая ошибка могла остановить процесс вычислений, и никто не мог снова запустить машину до утра понедельника. Это раздражало. А раздражение, как известно, — один из величайших стимулов технического прогресса. Хэмминг подумал, как было бы отлично, если машина смогла бы исправлять собственные ошибки и продолжать работать. В итоге он написал программу. Данные, которые вводятся в машину, можно представить в виде нулей и единиц, точно так же как и при передаче сообщений на спутник; с точки зрения математики не имеет значения, что представляют собой эти цифры: биты в цифровом потоке, состояние электрического реле или отверстия на перфоленте — в то время самый современный интерфейс передачи данных.

Первый шаг Хэмминга состоял в разбиении сообщения на блоки, состоящие из трех символов:

111 010 101…

Код Хэмминга — правило, в соответствии с которым каждый блок из трех цифр преобразуется в последовательность из семи цифр. Вот таблица кодирования:

000 → 0000000

001 → 0010111

010 → 0101011

011 → 0111100

101 → 1011010

110 → 1100110

100 → 1001101

111 → 1110001

Таким образом, кодированное сообщение будет выглядеть так:

1110001 0101011 1011010…

Перечисленные выше блоки из семи бит называются кодовыми словами. Эти восемь кодовых слов представляют собой единственные восемь блоков, которые разрешает данный код; если получатель видит что угодно другое, значит, что-то наверняка пошло не так. Предположим, вы получили блок 1010001. Вы знаете, что он не может быть правильным, потому что 1010001 — не кодовое слово. Более того, полученное вами сообщение отличается от кодового слова 1110001 всего на одну позицию. Другого кодового слова, которое было бы столь близким к искаженному сообщению, не существует. Следовательно, вы можете с довольно высокой степенью уверенности предположить, что кодовое слово, которое намеревался передать отправитель, — 1110001, а это означает, что соответствующий блок из трех цифр в исходном сообщении был 111.

Наверное, сейчас вы подумали, что нам просто повезло. Разве загадочное сообщение не могло быть близким к двум разным кодовым словам? В таком случае мы не имели бы возможности дать однозначную оценку. Но этого никогда не произойдет, и вот почему. Посмотрите еще раз на линии плоскости Фано:

124

135

167

257

347

236

456

Как бы вы описали данную геометрию компьютеру? Компьютеры любят, чтобы с ними разговаривали в нулях и единицах, поэтому нужно записать каждую линию в виде последовательности цифр 0 и 1, где 0 на позиции n означает «точка n находится на линии», а 1 на позиции n означает «точка n не находится на линии». Таким образом, первая линия, 124, будет представлена в таком виде:

0010111

а вторая, 135, — в таком:

0101011

Обратите внимание, что обе строки символов представляют собой кодовые слова из кода Хэмминга. В действительности семь ненулевых кодовых слов из кода Хэмминга в точности соответствуют семи линиям плоскости Фано. Код Хэмминга и плоскость Фано (а также, если уж на то пошло, оптимальная совокупность билетов для трансильванской лотереи) — один и тот же математический объект, но в разных нарядах!

Это и есть тайная геометрия кода Хэмминга. Кодовое слово представляет собой совокупность трех точек на плоскости Фано, образующих прямую линию. Изменение одного бита в строке равносильно прибавлению или исключению одной точки. Следовательно, если исходное кодовое слово было не 0000000, искаженное сообщение, которое вы получите, соответствует множеству из двух или из четырех точек. Если вы получите множество из двух точек, вам известно, как найти недостающую точку: это просто третья точка на единственной прямой, соединяющей две полученные вами точки. Что если вы получите множество из четырех точек, имеющее вид «прямая плюс одна дополнительная точка»? В таком случае вы можете сделать вывод, что правильное сообщение состоит из тех трех точек в вашем множестве, которые образуют прямую линию. Здесь есть одна тонкость: откуда вам известно, что существует только один способ выбора такого множества из трех точек? Давайте обозначим точки символами A, B, C и D. Если точки A, B и C лежат на прямой линии, тогда A, B и C должны быть тем самым множеством точек, которое намеревался передать вам отправитель. Но что если A, C и D также расположены на одной прямой? Не беспокойтесь: это невозможно, поскольку прямая, содержащая точки A, B и C, а также прямая, содержащая точки A, С и D, имели бы две общие точки — А и С. Однако две прямые линии могут пересекаться только в одной очке — таково правило. Другими словами, благодаря аксиомам геометрии код Хэмминга имеет такое же магическое свойство по исправлению ошибок, что и метод «повторить три раза»: если в процессе передачи в сообщении будет искажен один бит, получатель может вычислить, какое сообщение намеревался передать отправитель. Однако вместо увеличения времени передачи сообщения в три раза ваш новый усовершенствованный код позволяет отправлять семь бит на каждые три бита исходного сообщения, что обеспечивает более эффективный коэффициент 2,33.

Открытие кодов с исправлением ошибок, как первых кодов Хэмминга, так и разработанных впоследствии более эффективных кодов, преобразило проектирование информационных систем. Больше не требовалось создавать системы с двойной проверкой, нуждающиеся в столь сильной защите — защите, которая полностью исключала бы возможность ошибок. После открытий Хэмминга и Шеннона было достаточно сделать ошибки просто редкими, чтобы гибкость кода с исправлением позволяла нейтрализовать любые искажения. В настоящее время коды с исправлением ошибок используются в тех случаях, когда необходимо обеспечить быструю и надежную передачу данных. Орбитальный модуль Mariner 9 отправлял снимки поверхности Марса на Землю с использованием одного из таких кодов, кода Адамара. Компакт-диски кодируются с помощью кода Рида—Соломона — именно поэтому они звучат идеально, даже если их поцарапать. (Читатели, родившиеся после 1990 года и не знающие, что такое компакт-диски, могут просто вспомнить о картах флеш-памяти, в которых среди прочего используется код Боуза—Чоудхури—Хоквингема, чтобы предотвратить нарушение целостности данных.) Код вашего банка шифруется с помощью простого кода, который называется «контрольная сумма». Это не код с исправлением ошибок, а просто код с обнаружением ошибок, подобный протоколу «повторить каждый бит дважды». Если вы напечатаете одну цифру неправильно, компьютер, выполняющий перевод, может не понять, какое число вы на самом деле имели в виду, но он хотя бы определит, что что-то не так, и не отправит ваши деньги не в тот банк.

Не совсем ясно, когда именно Хэмминг понял весь диапазон применения своего нового метода, однако его руководство в Bell наверняка отдавало себе отчет, что стоит за его открытием. Хэмминг выяснил это, когда попытался опубликовать свою работу:

Патентный отдел не давал разрешение на публикацию до тех пор, пока не была обеспечена патентная защита… Я не верил, что они могут запатентовать кучку математических формул. Я так им и сказал. Они ответили: «Вот увидите». И были правы. С тех пор я понимаю, что плохо знаю патентное законодательство, поскольку часто бывает так, что вы вынуждены патентовать такие вещи, которые не нуждаются в этом, и это возмутительно.

Однако математика двигается вперед быстрее, чем патентное бюро. Швейцарский математик и физик Марсель Голей узнал об идеях Хэмминга от Шеннона и разработал много новых кодов, не зная о том, что Хэмминг разрабатывал такие же коды за завесой патентного права. Голей опубликовал свои работы первым, что повлекло за собой путаницу в отношении авторских прав, которая сохраняется до сих пор. Что касается патента, в Bell его получили, но потеряли право взимать деньги за лицензию в рамках антимонопольного соглашения 1956 года.

Что делает код Хэмминга столь эффективным? Чтобы понять это, необходимо взглянуть на ситуацию под другим углом и поставить вопрос так: что могло бы стать причиной его провала?

Помните: настоящее проклятие любого кода с исправлением ошибок — это блок цифр, который очень близок к двум разным кодовым словам одновременно. Получатель, в адрес которого отправлена проблемная комбинация битов, окажется в затруднительном положении, не имея надежного способа определить, какое из кодовых слов было в исходном сообщении.

Что мы имеем в виду, когда говорим про «близость» одного блока к другому? На первый взгляд может показаться, что мы используем метафору, поскольку блоки двоичных знаков не имеют местоположения. По твердому убеждению Хэмминга, понятие близости отнюдь не метафора и таковой не должна восприниматься — именно в этом и заключался его важный концептуальный вклад. Он ввел новое понятие расстояния, которое теперь называется расстоянием Хэмминга. Концепция расстояния была адаптирована к новой математике информации точно так же, как расстояние Евклида и Пифагора было адаптировано к геометрии плоскости. Хэмминг дал простое определение: расстояние между двумя блоками символов — это количество битов, которые необходимо изменить, чтобы превратить один блок в другой. Таким образом, расстояние между кодовыми словами 0010111 и 0101011 равно 4; чтобы превратить первое кодовое слово во второе, необходимо изменить биты во второй, третьей, четвертой и пятой позициях.

Восемь кодовых слов Хэмминга — хороший код, поскольку ни один блок из семи бит не находится на расстоянии Хэмминга между двумя кодовыми словами, равному 1. Если бы это было так, два кодовых слова были бы на расстоянии Хэмминга 2 друг от друга. Но вы можете проверить это сами — и увидите, что нет таких двух кодовых слов, которые отличались бы на две позиции; на самом деле расстояние Хэмминга между любыми двумя кодовыми ­словами равно 4. Вы можете провести аналогию между этими кодовыми словами и электронами в коробке или необщительными людьми в кабине лифта. Они находятся в ограниченном пространстве и в пределах этих ограничений пытаются расположиться как можно дальше друг от друга.

Этот же принцип лежит в основе всех возможных каналов коммуникации, устойчивых к помехам. Именно так устроен естественный язык: если я напишу lanvuage вместо language («язык»), вы поймете, что я имел в виду, поскольку в английском языке это единственное слово, которое можно получить посредством замены одной буквы в слове lanvuage. Безусловно, данный принцип не сработает при употреблении односложных слов: dog, cog, bog и log — каждое из этих слов имеет свое значение в английском языке, но всплеск шума, заглушающий первую фонему, не позволит распознать, что именно имелось в виду. Однако даже в таком случае можно использовать семантическое расстояние между словами, чтобы исправить ошибки. Если вас что-то укусило, значит, это dog («собака»); если вы с чего-то упали, то это log («бревно») и так далее.

Язык можно сделать более эффективным, но при этом возникает тот же негативный побочный эффект, с которым столкнулся Шеннон. В свое время многие люди, и упертые зануды и те, кто обладал математическими наклонностями, потратили массу усилий на создание языков, которые обеспечили бы компактную и точную передачу информации без всякой избыточности, синонимии и двусмысленности — всего того, чем грешат такие языки, как английский. Священник Эдвард Пауэлл Фостер создал в 1906 году искусственный язык Ро, с тем чтобы заменить дебри английского словаря лексиконом, в котором значение каждого слова можно было логически вывести из его звучания. Пожалуй, нет ничего удивительного в том, что среди горячих приверженцев языка Ро был Мелвилл Дьюи, который создал десятичную систему классификации, обеспечивающую расположение книг на полках библиотек в строгом порядке. Лаконичность языка Ро действительно заслуживает восхищения. Многие длинные английские слова, такие как ingredient, на языке Ро становятся гораздо короче — просто cegab. Однако подобная лаконичность имеет свою цену: она сопровождается потерей возможности исправлять ошибки, присутствующей в английском языке как встроенная функция. Это как маленькая, заполненная до отказа кабинка лифта, в которой у пассажиров нет дополнительного личного пространства. Другими словами, каждое слово на языке Ро очень похоже на многие другие слова, что создает возможности для путаницы. Например, на языке Ро «цвет» — это bofab. Но если вы измените всего одну букву, получаются следующие слова: «звук» — bogab; «электричество» — bokab; bolab — «вкус». Более того, в логической структуре языка Ро слова с похожим звучанием имеют похожее значение. Это обстоятельство еще больше усугубляет ситуацию, поскольку не позволяет по контексту понять, что происходит. Слова bofoc, bofof, bofog и bofol означают «красный», «желтый», «зеленый» и «голубой» соответственно. Концептуальное сходство звучания слов имеет свой смысл, но именно это затрудняет разговор, например, о том же цвете на той же людной вечеринке: «Простите, вы сказали “bofoc” или “bofog”?»

Впрочем, некоторые современные искусственные языки устроены иначе: в них используют принципы, сформулированные Хэммингом и Шенноном. Один из самых успешных примеров такого подхода — язык ложбан; в нем действует строгое правило, согласно которому два базовых корня (ginsu) не могут быть фонетически близкими.

Представление Хэмминга о расстоянии соответствует философии Фано: величина, которая крякает как расстояние, имеет право на то, чтобы вести себя как расстояние. Но нужно ли останавливаться на этом? Множество точек, расположенных от заданной центральной точки на расстоянии, меньшем или равном 1, имеет в евклидовой геометрии свое название: круг, или, в большей размерности, сфера. Таким образом, мы должны обозначить множество строк, расстояние Хэмминга которых от кодового слова не больше 1, термином «сфера Хэмминга», в центре которой находится кодовое слово. Для того чтобы код был кодом с исправлением ошибок, ни одна строка (ни одна точка, если серьезно относиться к этой аналогии) не может находиться на расстоянии 1 от двух разных кодовых слов; другими словами, требуется, чтобы две сферы Хэмминга с соответствующими кодовыми словами в центре не имели общих точек.

Таким образом, задача конструирования кодов с исправлением ошибок имеет такую же структуру, что и классическая геометрическая задача про упаковку сфер: каким образом разместить множество сфер одинакового размера в небольшом пространстве как можно плотнее, при условии что любые две сферы никогда не пересекутся? Проще говоря, сколько апельсинов можно уложить в ящик?

Задача упаковки сфер гораздо старше кодов с исправлением ошибок; этой проблемой занимался в свое время астроном Иоганн Кеплер, в 1611 году написавший на латинском языке трактат Strena, seu de nive sexangula («Новогодний подарок, или О шестиугольных снежинках») . Название довольно причудливое, но Кеплер на самом деле обращается к общим вопросам происхождения естественных форм. Почему снежинки и пчелиные соты образуют шестиугольники, тогда как семенная камера яблока состоит из пяти частей? Почему зерна граната имеют, как правило, двенадцать плоских сторон? Кстати последний вопрос имеет самое непосредственное отношение к нашей современной жизни.

Посмотрим, что по этому поводу говорит Кеплер. Гранатовое дерево стремится поместить под кожицей своего плода как можно больше зерен; другими словами, оно решает задачу упаковки сфер. При условии, что природа делает свою работу очень качественно и сверхответственно, эти сферы должны быть размещены с максимальной плотностью. Кеплер предложил, по его утверждению, самый оптимальный вариант упаковки сфер. Для укладки нижнего слоя следует начать с плоской стороны зерен, расположив их таким традиционным образом, как показано на рисунке.

Следующий слой должен выглядеть аналогично, но зернышки необходимо выложить так, чтобы каждое разместилось в маленьком треугольном углублении, образованном тремя зернами нижнего слоя. Затем необходимо точно так же выкладывать следующие слои зерен граната. При укладке требуется проявлять некоторую осторожность: только половина углублений будет поддерживать сферы следующего уровня, и на каждом этапе предстоит решать, какую именно половину углублений вы хотите заполнить. Традиционное решение, которое называется «гранецентрированная кубическая решетка», имеет одно замечательное свойство: на каждом очередном уровне есть сферы, расположенные непосредственно над сферами тремя уровнями ниже. По мнению Кеплера, не существует способа более плотной упаковки сфер в пространстве. В гранецентрированной кубической решетке каждая сфера соприкасается ровно с двенадцатью другими сферами. Кеплер считал, что по мере роста зерен граната каждое из них начинает придавливать своих двенадцать соседей, из-за чего поверхность у точки соприкосновения становится плоской и зерна граната превращаются в фигуры с двенадцатью гранями.

Понятия не имею, был ли прав Кеплер насчет граната, но его утверждение, что гранецентрированная кубическая решетка обеспечивает самую плотную упаковку сфер, на целые столетия оказалось в центре пристального интереса математиков. Кеплер не сформулировал доказательство своего утверждения; по всей вероятности, ему просто казалось очевидным, что гранецентрированную кубическую решетку превзойти невозможно. С ним солидарны целые поколения бакалейщиков, пакующие апельсины в соответствии с гранецентрированной кубической конфигурацией. Однако математикам как людям требовательным понадобилось абсолютное подтверждение, причем не только в отношении окружностей и сфер. В мире чистой математики ничто не мешает выйти за рамки окружностей и сфер, устремиться к более высоким размерностям и начать упаковать так называемые гиперсферы в пространство с количеством измерений больше трех. Не позволяет ли геометрическая история об упаковке сфер в пространстве с большей размерностью лучше понять теорию кодов с исправлением ошибок, подобно геометрической истории о проективном плане? В данном случае поток перемещается главным образом в другом направлении: открытия в области кодирования подстегнули прогресс в области упаковки сфер. Например, в 1960-е годы Джон Лич, применив один из кодов Голея, построил в двадцатичетырехмерном пространстве невероятно плотную упаковку сфер. Конфигурация, известная сегодня как «решетка Лича», представляет собой крайне густонаселенное место, в котором каждая из двадцатичетырехмерных сфер соприкасается с 196 560 соседними сферами. До сих пор неизвестно, обеспечивает ли она самую плотную упаковку сфер в двадцатичетырехмерном пространстве, но в 2003 году Генри Кон и Абхинав Кумар доказали, что, если более плотная решетка и существует, она обеспечит плотность упаковки сфер больше плотности решетки Лича максимум в

1,0­00­000­000­000­000­000­000­000­000­001­65 раз,

то есть довольно близко к решетке Лича .

Я пойму вас и даже прощу, если вы скажете, что вам, мол, нет никакого дела до двадцатичетырехмерных сфер и того, как можно их упаковать. Но важно понимать один момент: любой математический объект, столь невероятный, как решетка Лича, приобретает весьма большое значение, и к нему должно отнестись крайне серьезно. Как выяснилось, решетка Лича содержит множество симметрий поистине экзотического вида — Джон Конвей, крупный специалист в области теории групп, узнал о ней в 1968 году, за двадцать четыре часа непрерывных вычислений он выписал на огромный рулон бумаги все симметрии решетки Лича. В конечном счете эти симметрии позволили сформулировать последние фрагменты теории конечных групп симметрии, занимавшей умы алгебраистов на протяжении большей части ХХ столетия.

Что касается старых добрых трехмерных апельсинов… Оказывается, Кеплер был прав, настаивая, что его способ упаковки самый лучший, но это не было доказано еще целых четыре столетия, пока в 1998 году теорию Кеплера не подтвердил Томас Хейлс, в то время профессор Мичиганского университета. Хейлс решил этот вопрос с помощью сложного и изящного доказательства, в котором задача была сведена к анализу всего лишь нескольких тысяч сфер, выполненному посредством большого объема компьютерных вычислений. Для математического сообщества не проблема создать сложное и изящное доказательство (мы привыкли к такого рода трудам), и эта часть работы Хейлса быстро получила превосходную оценку и подтверждение правильности; но что касается большого объема компьютерных вычислений — тут сложилась более серьезная ситуация. Доказательство возможно проанализировать до последней детали, однако с компьютерной программой все обстоит иначе. Теоретически человек в состоянии проверить каждую строку кода, но, даже если он с этим справится, может ли он полагаться на то, что код будет выполняться корректно?

Почти все математики признали доказательство ученого, но, по всей видимости, самолюбие Хейлса было сильно задето сомнением коллег по поводу того, что при доказательстве ему пришлось воспользоваться компьютерными вычислениями. После подтверждения гипотезы Кеплера он отошел от геометрии, которая сделала его знаменитым, и занялся проектом формальной верификации доказательств. Хейлс предвидит появление математики будущего, отличной от современной, и работает над ее созданием. Он считает, что математические доказательства, независимо от того, как они выполнены — с помощью ли компьютера или с помощью карандаша и бумаги, — стали настолько сложными и взаимозависимыми, что мы больше не можем быть полностью уверенными в их корректности. Классификация конечных простых групп — к настоящему времени завершившийся проект, важной частью которого стал выполненный Конвеем анализ решетки Лича, — состоит из сотен работ сотен авторов. В итоге их труд занимает около десяти тысяч страниц, и не приходится утверждать, что хотя бы один человек из ныне живущих понимает его целиком. Так как мы можем быть уверены в его правильности?

По мнению Хейлса, у нас нет иного выбора, кроме как начать все с самого начала, перестроив всю совокупность математических знаний в пределах формальной структуры, которую можно будет проверять с помощью компьютера. Коль скоро код, проверяющий формальные доказательства, сам поддается проверке (с точки зрения Хейлса, эта цель вполне достижима), мы можем навсегда избавиться от споров вокруг проблемы, с которой столкнулся в свое время Хейлс, — действительно ли доказательство является доказательством. Что будет дальше? Возможно, на следующем этапе появятся компьютеры, способные конструировать доказательства или даже генерировать идеи без какого бы то ни было вмешательства человека.

Если так и произойдет, наступит ли конец математики? Безусловно. В том случае, если машины догонят, а затем и превзойдут человека во всех областях мыслительной деятельности; если они начнут использовать нас в качестве рабов, скота или игрушек, как предсказывают некоторые самые смелые футуристы, — тогда да, математике придет конец, как, собственно, и всему остальному. Но если исключить такой вариант, то математика, должно быть, выживет. По крайней мере хочется так думать. Если на то пошло, математика уже десятки лет обращается за помощью к компьютерам. Многие вычисления, которые в прошлом мы отнесли бы к категории исследований, сейчас считаются не более творческими или достойными похвалы, чем сложение ряда десятизначных чисел. Если что-то может сделать ваш ноутбук, значит, это что-то уже не математика. Тем не менее данное обстоятельство не оставило математиков без работы. Мы смогли сохранить свои позиции при каждодневно растущем доминировании компьютерной сферы. Мы продолжаем работать на опережение, подобно киногероям, обгоняющим огненный шар.

Если даже искусственный интеллект будущего сможет взять на себя большую часть работы, которая сегодня квалифицируется как научная деятельность, мы просто переведем эти исследования в категорию вычислений. А все, чем мы, люди с математическим складом ума, захотим заняться в освободившееся время, мы называем математикой.

Код Хэмминга довольно хорош, но наверняка найдется кто-то, рассчитывающий, что ему удастся создать код более совершенный. В конце концов, в коде Хэмминга присутствует определенная избыточность: даже во времена перфолент и механических реле компьютеры были настолько надежны, что почти все блоки из семи бит передавались без искажений. Этот код кажется слишком консервативным: мы вполне могли бы обойтись включением меньшего количества защитных битов в свои сообщения. И мы действительно можем это сделать — доказательством тому служит знаменитая теорема Шеннона. Например, если ошибки происходят с частотой одна ошибка на тысячу бит, Шеннон утверждает, что есть коды, которые сделают каждое сообщение всего на 1,2% длиннее, чем то же сообщение без кода. Более того, делая базовые блоки все более длинными, можно найти коды, обеспечивающие заданную скорость и удовлетворяющие любым требованиям к надежности, какими бы жесткими они ни были.

Как Шеннон сконструировал свои безупречные коды? На самом деле ответ очень прост: он этого не делал. Когда мы встречаем такую сложную конструкцию, как код Хэмминга, то, разумеется, склонны думать, будто код с исправлением ошибок представляет собой некий особый код, который сначала разрабатывают, затем вносят в него изменения, после чего пишут его снова — и так до тех пор, пока каждая пара кодовых слов не окажется осторожно разделенной, но при этом любые другие два кодовых слова не будут находиться слишком близко друг к другу. Гениальность Шеннона состояла в том, что он понял всю необоснованность подобных представлений. В кодах с исправлением ошибок нет ничего особенного. Шеннон доказал — это было не сложно, как только он понял, что именно нужно доказывать, — что почти все наборы кодовых слов обладают свойством исправления ошибок. Другими словами: совершенно случайный код, не имеющий никакой структуры, с очень большой вероятностью является кодом с исправлением ошибок.

Это было поразительное открытие, если не сказать больше. Представьте себе, что вам дали задание построить аппарат на воздушной подушке. Вряд ли вы начнете с того, что в беспорядке разбросаете на земле кучу резиновых трубок и деталей двигателя, рассчитывая, что то, что получилось, полетит.

Хэмминг в 1986 году посвятил Шеннону почти восторженные слова — даже сорок лет спустя его открытие производило на математиков огромное впечатление:

Храбрость — качество, которым Шеннон владел в полной мере. Достаточно вспомнить о его главной теореме. Он хочет создать метод кодирования, но не знает, что делать, поэтому создает случайный код. Затем он заходит в тупик. А после задает невероятный вопрос: «Что сделал бы обычный случайный код?» Позже он доказывает, что обычный код вполне хорош, а значит, должен существовать как минимум один хороший код. Кто кроме человека беспредельной храбрости посмел бы размышлять о чем-то подобном? Это и есть черта великих ученых: им свойственна храбрость. Они идут вперед при невообразимых обстоятельствах; они никогда не прекращают мыслить.

Но если случайный код с большой вероятностью может быть кодом с исправлением ошибок, в чем смысл кода Хэмминга? Почему просто не выбрать кодовые слова совершенно случайным образом, опираясь на знание — согласно теореме Шеннона, — что этот код, по всей вероятности, будет исправлять ошибки? Вот одна из проблем этого плана. Недостаточно, чтобы код в принципе был способен исправлять ошибки; он должен быть применимым на практике. Если в одном из кодов Шеннона используются блоки размером 50, тогда количество кодовых слов равно количеству строк из 0–1 длиной 50 бит, что составляет 2 в степени 50, немногим более квадриллиона. Большое число. Ваш космический корабль получает сигнал, который предположительно является одним из квадриллиона кодовых слов или как минимум близок к одному из них. Но какое именно кодовое слово? Не перебирать же квадриллион кодовых слов по одному! Снова происходит комбинаторный взрыв, и в данном контексте это влечет за собой еще один компромисс. Коды со сложной структурой, такие как коды Хэмминга, в большинстве случаев легко декодировать. Однако сугубо специальные коды оказались не столь эффективными, как совершенно случайные коды, которые изучал Шеннон! За прошедшие с тех пор десятилетия, вплоть до настоящего времени, математики пытались одолеть эту границу между структурой и случайностью, кропотливо работая над созданием оптимальных кодов — достаточно случайных, чтобы быть быстрыми, и достаточно структурированных, чтобы поддаваться декодированию.

Код Хэмминга прекрасно подходит для трансильванской лотереи, но он неэффективен в случае лотереи Cash WinFall. В трансильванской лотерее всего семь чисел, в лотерее штата Массачусетс их сорок шесть. Следовательно, нам понадобится код побольше. Лучший код, который мне удалось найти для этой цели, открыл в 1976 году Ральф Деннистон из Лестерского университета. И это очень красивый код.

Деннистон составил список из 285 384 комбинаций шести чисел из сорока восьми. Этот список начинается так:

1 2 48 3 4 8

2 3 48 4 5 9

1 2 48 3 6 32

В первых двух билетах четыре общие числа: 2, 3, 4 и 48. Однако (в этом и заключается поразительная особенность системы Деннистона) среди всех этих 285 384 лотерейных билетов вы не найдете пяти совпадающих чисел. Систему Деннистона можно перевести в код, как мы сделали это с плоскостью Фано, — заменив числа каждого билета строкой из 48 единиц и нулей, в которой 0 стоит на позициях, соответствующих числам вашего билета, а 1 — на позициях, соответствующих числам, которых в билете нет. Таким образом, первый билет из приведенных выше можно представить в виде такого кодового слова:

00­00­11­10­11­11­11­11­11­11­11­11­11­11­11­11­11­11­11­11­11­11­11­10

Проверьте сами: тот факт, что среди всех этих лотерейных билетов нет двух билетов с пятью совпадающими числами из шести, означает, что этот код, подобно коду Хэмминга, не содержит два кодовых слова, разделенных расстоянием Хэмминга, меньшим четырех.

Это можно сформулировать так: каждая комбинация из пяти чисел присутствует в максимум одном из билетов Деннистона. На самом деле все даже лучше: по существу, каждая комбинация из пяти чисел присутствует ровно в одном билете.

Можете представить, какой тщательности требует выбор комбинаций чисел, входящих в список Деннистона? Деннистон включил в свою работу компьютерную программу на языке алгол, которая проверяет список на предмет того, действительно ли он обладает заявленным магическим свойством — для 1970-х годов жест довольно прогрессивный. Тем не менее Деннистон настаивает, что роль компьютера в этой работе следует расценивать как вторичную по отношению к его собственной: «На самом деле я хотел бы заявить, что все объявленные здесь результаты были получены без использования компьютера, хотя я допускаю, что их можно проверить с помощью компьютеров».

В лотерее Cash WinFall всего сорок шесть чисел, поэтому, чтобы сыграть в нее по методу Деннистона, придется немного нарушить красивую симметрию его системы, выбросив из его списка все билеты с числами 47 и 48. После этого у вас все еще останется 217 833 лотерейных билета. Предположим, вы достанете из тайника 435 666 долларов и решите поиграть в числа. Что произойдет?

В розыгрыше лотереи выпадает по шесть чисел — скажем, 4, 7, 10, 11, 34 и 46. Если произойдет маловероятное событие, эти числа совпадут с числами в одном из ваших лотерейных билетов — и вы получаете джекпот. Но даже если этого не произойдет, вы все равно сможете выиграть кучу денег по тем лотерейным билетам, в которых совпадут пять из шести чисел. Есть ли у вас билет с числами 4, 7, 10, 11, 34? В одном из билетов Деннистона такие числа есть, а значит, единственный случай, когда у вас не окажется такого билета, — если в нем были числа 4, 7, 10, 11, 34, 47 или 4, 7, 10, 11, 34, 48, поэтому вы его выбросили.

Но как насчет другой комбинации из пяти чисел, скажем 4, 7, 10, 11, 46? Может быть, вам не повезло в первый раз, потому что билет с числами 4, 7, 10, 11, 34, 47 был одним из билетов Деннистона. Но в таком случае билет 4, 7, 10, 11, 46, 47 не может быть в списке Деннистона, поскольку пять чисел этого билета совпадают с пятью числами билета, который, как вам известно, входит в этот список. Другими словами, если из-за злополучного числа 47 вы упустите один из призов за пять угаданных чисел, это не приведет к тому, что вы упустите и все остальные призы. То же самое можно сказать и о числе 48. Вот список возможных выигрышных билетов в категории «Пять угаданных чисел из шести»:

4, 7, 10, 11, 34

4, 7, 10, 11, 46

4, 7, 10, 34, 46

4, 7, 11, 34, 46

4, 10, 11, 34, 46

7, 10, 11, 34, 46

Минимум четыре из этих билетов гарантированно окажутся среди ваших. В действительности, если вы купите 217 833 лотерейных билета Деннистона, у вас будет такая вероятность выигрыша:

вероятность выиграть джекпот составляет 2%;

вероятность выиграть шесть призов в категории «Пять из шести» составляет 72%;

вероятность выиграть пять призов в категории «Пять из шести» составляет 24%;

вероятность выиграть четыре приза в категории «Пять из шести» составляет 2%.

Сравните этот подход со стратегией Селби, который выбирал числа случайным образом с помощью функции Quic Pick. В этом случае существует небольшая вероятность 0,3% вообще потерять все призы категории «Пять угаданных чисел из шести». Более того, вероятность выиграть только один приз этой категории составляет 2%, два приза — 6%, три приза — 11% и четыре приза — 15%. Гарантированная прибыльность стратегии Деннистона уступает место риску. Безусловно, у этого риска есть свое преимущество: команда Селби может выиграть более шести таких призов с вероятностью 32%, что невозможно в случае выбора лотерейных билетов по системе Деннистона. Билеты Селби, билеты Деннистона и любые другие билеты имеют одну и ту же ожидаемую ценность, однако метод Деннистона защищает игрока от воли случая. Чтобы играть в лотерею, ничем не рискуя, недостаточно играть сотнями тысяч билетов; необходимо играть правильными сотнями тысяч билетов.

Является ли эта стратегия причиной того, что члены группы Random Strategies тратили так много времени на заполнение сотен тысяч лотерейных билетов вручную? Использовали ли они систему Деннистона, разработанную в духе чистой математики, ради того чтобы выкачать деньги из лотереи без всякого риска для себя? Здесь мои изыскания зашли в тупик. Мне удалось связаться с Юраном Ли, но он не знал наверняка, как выбирались эти билеты; он сказал только, что у них в общежитии был человек, к которому они обращались за помощью и который занимался всеми вопросами, связанными с алгоритмом выбора чисел. Я не уверен, использовал ли этот человек систему Деннистона или что-то в этом роде. Но если нет, то думаю, ему следовало бы так поступить.

ТАК И БЫТЬ, МОЖЕТЕ ИГРАТЬ В ЛОТЕРЕЮ

К настоящему моменту мы всеми возможными способами обосновали вывод о том, что решение играть в лотерею почти всегда является неудачным с точки зрения ожидаемого количества денег, а также что в тех редких случаях, когда ожидаемая денежная стоимость лотерейного билета превышает его цену, необходимо очень тщательно подходить к вопросу извлечения максимальной пользы из тех билетов, которые вы покупаете.

Учитывая все это, экономистам с математическим складом мышления придется объяснить один неудобный факт — тот самый, что более двух сотен лет назад озадачил Адама Смита. Лотереи очень и очень популярны. Дело в том, что лотерея — совсем не та ситуация, которую изучал Эллсберг. Когда люди сталкиваются с проблемой принятия решений при неизвестных обстоятельствах, которые невозможно установить. Крошечный шанс выиграть в лотерею выставлен на всеобщее обозрение. Закон, гласящий, что люди склонны принимать решения, которые в той или иной степени приносят им максимальную пользу, является одним из столпов экономики и действительно позволяет моделировать поведение в самых разных областях, от ведения бизнеса до выбора спутника жизни. Но это не касается лотереи. Для определенной категории экономистов такое иррациональное поведение в такой же мере неприемлемо, как для пифагорейцев была неприемлемой иррациональная длина гипотенузы. Подобное не вписывается в их модель происходящего — и все же оно имеет место быть.

Экономисты мыслят более гибко, чем пифагорейцы. Вместо того чтобы в ярости топить гонцов с плохими вестями, они адаптируют свои модели к реальности. Одну известную интерпретацию предложили наши старые друзья Милтон Фридман и Леонард Сэвидж, которые предположили, что игроки в лотерею придерживаются волнообразной кривой полезности, отображающей тот факт, что люди думают о богатстве в категориях классов, а не в количественных величинах. Если вы, будучи представителем среднего класса, тратите на лотерею пять долларов в неделю и проигрываете, такое решение обходится вам в небольшую сумму денег, но не меняет ваш социальный статус: несмотря на потерю денег, отрицательная полезность почти близка к нулю. Но, если вы выиграете, это переведет вас в другую социальную группу. Вы можете считать это моделью «смертного одра»: когда вы окажетесь при смерти, будет ли вас беспокоить мысль, что вы умираете с несколько меньшим количеством денег — и все потому, что любили играть в лотерею? По всей вероятности, нет. Будет ли для вас иметь значение тот факт, что в тридцать пять лет вы ушли на пенсию и остаток жизни провели где-то на Карибских островах, занимаясь подводным плаваньем, — и все потому, что выиграли большой приз в лотерею? Да, будет.

Еще больше отдалившись от классической теории, Даниель Канеман и Амос Тверски выдвинули предположение, что люди в основном склонны придерживаться образа действий, отличающегося от того, что предписывает кривая полезности, причем не только когда Дэниел Эллсберг ставит перед ними свою урну, но и в целом в жизни. Их работа о теории перспектив, за которую Канеман впоследствии получил Нобелевскую премию, рассматривается сейчас в качестве основополагающей в концепции бихевиористской экономики, чья задача состоит в создании максимально точной модели поведения людей: как они действуют на самом деле, а не как должны действовать согласно абстрактной концепции рациональности. Теория Канемана—Тверски гласит: люди склонны придавать маловероятным событиям большее значение по сравнению с человеком, придерживающимся аксиом Неймана—Моргенштерна. Именно поэтому притягательность джекпота превосходит уровень, который можно было бы считать приемлемым согласно строгой оценке ожидаемой полезности.

Однако самое простое объяснение не требует никаких сложных теоретических выкладок. Все просто: лотерейный билет, независимо от того, выиграете вы или нет, в каком-то смысле просто развлечение. Развлечение не того уровня, как отдых на Карибских островах или танцы всю ночь напролет, но все-таки… Стоит ли оно одного-двух долларов? Видимо, да. Есть основания поставить это объяснение под вопрос (сами игроки в лотерею называют перспективу выигрыша в качестве основной причины для игры), но оно наилучшим образом проливает свет на то поведение, которое мы видим.

Экономика — это не физика, а полезность — это не энергия. Полезность не сохраняется, подобно энергии, а взаимодействие между двумя людьми может оставить их с большей полезностью, чем то, с чего они начинали. Лотерея — это не регрессивный налог, а игра, когда люди платят штату небольшие комиссионные за несколько минут развлечения, которое штат может организовать с минимумом затрат. Кстати, благодаря вырученным средствам библиотеки будут работать и уличные фонари будут светить. Подобно тому как две страны торгуют друг с другом, в случае с лотереей выигрывают обе стороны сделки.

Поэтому, да — играйте в лотерею, если она приносит вам удовольствие. Математика вам это разрешает!

Безусловно, такая точка зрения не лишена недостатка. Приведу еще одну мысль Паскаля; он дает, как всегда, мрачную оценку возбуждению, которое вызывают азартные игры:

Вот этот человек живет, не скучая: он всякий день играет по малой. Давайте ему каждое утро ту сумму, которую он может выиграть днем, но потребуйте, чтобы он отказался от игры: вы сделаете его несчастным. Возможно, кто-то скажет, что он играет для забавы, а не для выигрыша. Тогда заставьте его играть не на деньги: он охладеет к игре и заскучает. Значит, он ищет не просто забавы. Забава без риска и страсти нагонит на него скуку. Ему нужно горячительное, нужно возбуждать себя мыслью, будто он будет счастлив, выиграв сумму, которой не пожелал бы, если б ему ее предложили с условием отказаться от игры… 

Паскаль считает презренным удовольствие от азартных игр. А если это удовольствие выходит за рамки разумного, то, конечно оно может навредить человеку. Подобные рассуждения оборачиваются своей обратной стороной и начинают звучать в поддержку лотерей. Предполагаю, что продавцы метамфетамина и их клиенты поддерживают такие же взаимовыгодные отношения. Говорите о метамфетамине все, что хотите, но вы не можете отрицать: многие люди получают от него настоящее удовольствие.

Как насчет другого сравнения? Оставим наркоманов и подумаем о владельцах малого бизнеса, гордости Америки. Открытие магазина или продажа услуг — отнюдь не то же самое, что покупка лотерейных билетов. Ведя свой небольшой бизнес, вы в какой-то степени контролируете собственный успех. Однако у этих двух явлений есть нечто общее: для большинства людей открытие компании — это заведомо проигрышное дело. Не имеет значения, насколько вкусным будет ваш соус для барбекю, или насколько новаторским будет ваше приложение, или насколько жесткими будут ваши методы ведения бизнеса, — у вас гораздо больше шансов потерпеть неудачу, чем добиться успеха. Такова природа предпринимательства, поскольку вы балансируете на грани между очень низкой вероятностью разбогатеть, довольно большой вероятностью зарабатывать на жизнь тяжелым трудом и существенно высокой вероятностью потерять все свои деньги. Если подсчитать цифры, для большой части потенциальных предпринимателей ожидаемая финансовая ценность, подобно ценности лотерейного билета, окажется меньше нуля. Обычные предприниматели (как и обычные покупатели лотерейных билетов) переоценивают свои шансы на успех. Даже бизнес, которому удается уцелеть, обычно приносит своим владельцам меньше денег, чем они получили бы в виде заработной платы в успешной компании. Тем не менее общество в целом выигрывает от существования мира, в котором люди вопреки здравому смыслу начинают свой бизнес. Нам нужны рестораны, нужны парикмахерские, нужны игры для смартфонов. Можно ли назвать предпринимательство «налогом на глупость»? Вас назвали бы сумасшедшим, если вы посмели бы сказали нечто подобное. Отчасти это объясняется тем, что мы относимся к владельцу бизнеса с большим уважением, чем к азартному игроку, поскольку нам трудно отделить свои нравственные установки в отношении той или иной деятельности от суждений, которые мы делаем по поводу рациональности. Однако полезность ведения бизнеса измеряется не только в ожидаемой денежной стоимости. Сам акт осуществления мечты или даже попытки ее осуществить — уже есть часть вознаграждения.

Как бы там ни было, именно к такому выводу пришли Джеймс Харви и Юран Лу. После закрытия лотереи WinFall они переехали на запад и основали в Кремниевой долине стартап, который продает компаниям системы для ведения переговоров в онлайновом режиме. (На странице Харви среди его интересов есть такой скромный пункт: «нетрадиционные инвестиционные стратегии».) В момент написания этих строк Харви и Лу все еще ищут венчурный капитал. Может быть, они его когда-нибудь получат. Если нет, держу пари, что вскоре они снова начнут новый бизнес — какой бы ни была ожидаемая ценность — в расчете на то, что следующая ставка, которую они сделают, окажется выигрышной.

Отправить

Антон

Перезвоните мне пожалуйста 8 (953) 367-35-45 Антон.