ГЛАВА ДВЕНАДЦАТАЯ
ЧАЩЕ ОПАЗДЫВАЙТЕ НА САМОЛЕТЫ!
Лауреат Нобелевской премии по экономике за 1982 год Джордж Стиглер говорил: «Если вы никогда не опаздываете на самолет, значит, вы проводите слишком много времени в аэропорту». На первый взгляд это утверждение кажется парадоксальным, особенно если недавно вы действительно опоздали на самолет. Когда я застреваю в аэропорту О’Хара и ем там ужасный куриный ролл «Цезарь» за 12 долларов, я редко отдаю должное своему экономическому здравому смыслу. Однако, каким бы необычным ни казалось утверждение Стиглера, вычисление ожидаемой ценности показывает, что оно абсолютно корректно — во всяком случае для тех, кто много летает. Для простоты мы можем проанализировать всего три варианта.
Вариант 1. Прибытие в аэропорт за 2 часа до вылета, опоздание на самолет в 2% случаев.
Вариант 2. Прибытие в аэропорт за 1,5 часа до вылета, опоздание на самолет в 5% случаев.
Вариант 3. Прибытие в аэропорт за 1 час до вылета, опоздание на самолет в 15% случаев.
Безусловно, во сколько вам обойдется опоздание на самолет, в значительной мере зависит от ситуации: одно дело — опоздать на челночный рейс до округа Колумбия и сесть на следующий, и совсем другое — опоздать на последний рейс, пытаясь попасть на свадьбу, которая состоится завтра в десять утра. В лотерее как цена билета, так и размер приза выражены в долларах. Гораздо менее очевидно, как можно определить ценность времени, которое мы можем потратить зря, сидя в терминале аэропорта, в сравнении с ценностью опоздания на самолет. И то и другое вызывает раздражение, однако общепризнанной денежной единицы раздражения не существует.
Во всяком случае, такой денежной единицы нет на бумаге. Однако решения необходимо принимать, и экономисты стремятся рассказать нам, как это делать, а значит, необходимо сконструировать некую версию доллара раздражения. В экономике принято считать: если люди действуют рационально, они принимают решения, которые максимально увеличивают полезность этих решений. В жизни все имеет полезность; хорошие вещи, такие как деньги или торт, имеют положительную полезность, тогда как плохие вещи, такие как пальцы ног, которые вы ушибли, и самолеты, на которые вы опоздали, имеют отрицательную полезность. Некоторые даже предпочитают измерять полезность в стандартных единицах под названием «ютили». Предположим, один час вашего времени дома стоит один ютиль; в таком случае прибытие в аэропорт за два часа до вылета обойдется вам в два ютиля, тогда как прибытие за один час — один ютиль. Опоздание на самолет явно хуже потраченного зря часа времени. Если вы считаете, что опоздание стоит шесть часов вашего времени, тогда можете приравнять упущенный рейс к шести ютилям.
Если мы переведем все в ютили, это позволит нам сравнить ожидаемую ценность трех стратегий.
| Вариант 1 | −2 + 2% × (−6) = −2,12 ютиля |
| Вариант 2 | −1,5 + 5% × (−6) = −1,8 ютиля |
| Вариант 3 | −1 + 15% × (−6) = −1,9 ютиля |
Вариант 2 — именно тот, который в среднем обойдется вам в самое меньшее количество ютилей, хотя он и сопровождается ненулевой вероятностью опоздания на самолет. Да, надолго застрять в аэропорту — утомительно и неприятно, но разве настолько, чтобы раз за разом проводить лишних полчаса в терминале, чтобы сократить и без того небольшой шанс опоздать на самолет?
Может быть, вы ответите утвердительно. Может быть, вы не любите опаздывать на самолет, и опоздание обойдется вам в двадцать ютилей, а не в шесть. В таком случае представленные выше расчеты изменятся и предпочтительным станет консервативный вариант 1 с ожидаемой ценностью
−2 + 2% × (−20) = −2,4 ютиля.
Но это не значит, что Стиглер неправ; это просто переводит компромисс в другое место. Вы могли бы сократить вероятность опоздания на самолет еще больше, приехав в аэропорт за три часа до вылета. Тем не менее такой шаг, даже если он сократит вероятность опоздания до нуля, неизбежно обойдется вам в 3 ютиля, а это хуже варианта 1. Если отобразить на графике количество часов, которые вы проводите в аэропорту, вместе с ожидаемой ценностью каждого варианта, получится такая картина.
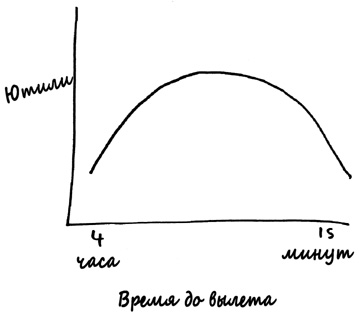
Но это снова кривая Лаффера! Прибытие в аэропорт за пятнадцать минут до вылета сопряжено с высокой вероятностью опоздания со всей отрицательной полезностью, которую это подразумевает. С другой стороны, прибытие в аэропорт за много часов до вылета также обойдется вам во много ютилей. Оптимальный образ действий находится где-то посередине, но где именно — зависит от вашего восприятия относительных преимуществ опоздания на самолет и напрасной потери времени. Если вы никогда не опаздываете на самолет, значит, ваш выбор смещен влево от оптимальной стратегии. Как и говорит Стиглер, вам следует экономить свои ютили и чаще опаздывать на самолет.
Безусловно, такие расчеты носят сугубо субъективный характер: ваш дополнительный час в аэропорту может обойтись вам не во столько же ютилей, во сколько обходится мне. (Я на самом деле терпеть не могу куриные роллы «Цезарь».) Следовательно, от этой теории нельзя ожидать, что она выдаст вам точное время прибытия в аэропорт или точное количество самолетов, на которые следует опоздать. Результат этих расчетов носит качественный, а не количественный характер. Я не знаю, какова самая подходящая для вас вероятность опоздания на самолет; я знаю только, что она не равна нулю.
Одно предостережение: на практике вероятность, близкую к нулю, бывает трудно отличить от нулевой вероятности. Если вы экономист мирового уровня, часто летающий на самолетах, принятие риска опоздания на самолет в размере 1% может означать, что вы будете опаздывать на самолет каждый год. Для большинства обычных людей такой низкий уровень риска мог бы означать, что они за всю свою жизнь не опоздают ни на один самолет. Следовательно, если 1% — приемлемый для вас уровень риска, и если вы всегда успеваете на самолет, то это не значит, что вы делаете что-то неправильно. Точно так же не следует использовать аргумент Стиглера для обоснования следующего утверждения: «Если вы никогда не разбивали машину вдребезги, значит, вы ездите слишком медленно». Стиглер сказал бы: если вы вообще не рискуете разбить свою машину вдребезги, значит, вы ездите слишком медленно, что совершенно верно: единственный способ полностью исключить риск состоит в том, чтобы вообще не ездить!
Аргументация в стиле Стиглера — это полезный инструмент для самых разных задач оптимизации. Рассмотрим хотя бы расточительство правительства: не проходит и месяца, чтобы вы не прочитали в газетах о государственном служащем, который обошел правила системы, чтобы получить завышенную пенсию, или о военном подрядчике, заключившем контракт с Министерством обороны по абсурдно высоким ценам, или о городском агентстве, которое уже давно исчерпало свои функции, но по-прежнему существует за счет населения города благодаря инертности городских властей и влиятельным покровителям. Вот фрагмент из типичной статьи такого рода, опубликованной в Wall Street Journal:
В понедельник генеральный инспектор управления социальной защиты США заявил, что агентство ошибочно выплатило социальных пособий на сумму 31 миллион долларов 1546 американцам, которые предположительно уже скончались.
Генеральный инспектор сказал, что еще больше усугубляет ситуацию тот факт, что информация о смерти каждого из этих людей была подана управлением социальной защиты в государственную базу данных, а это значит, что в агентстве должны были знать о смерти этих американцев и остановить платежи.
Почему мы допускаем существование подобных ситуаций? Ответ прост: устранение потерь имеет свою цену, так же как заблаговременное прибытие в аэропорт имеет свою цену. Обеспечение соблюдения правил и бдительность — это достойные цели, но устранение всех потерь, подобно устранению малейшей вероятности опоздать на самолет, влечет за собой затраты, которые перевешивают преимущества. Как отметил блогер (и в прошлом участник математических олимпиад) Николас Бодро, 31 миллион долларов составляет всего 0,004% от общей суммы социальных пособий, выплачиваемых управлением социальной защиты за год. Другими словами, агентство уже и так прекрасно справляется с задачей получения информации о том, кто жив, а кто покинул этот мир. Попытки еще более эффективно проводить это различие с целью устранения последних немногочисленных ошибок могут обойтись очень дорого. Если мы хотим подсчитать количество ютилей, мы не должны спрашивать: «Почему мы зря тратим деньги налогоплательщиков?» Вопрос следует ставить так: «Какова разумная сумма денег налогоплательщиков, которую допустимо потратить зря?» Перефразируя Стиглера, можно сказать следующее: если ваше правительство совсем не транжирит, вы тратите слишком много времени на то, чтобы бороться с правительственным транжирством.
ЕЩЕ РАЗ О БОГЕ — И НА ЭТОМ ПОСТАВИМ ТОЧКУ, ОБЕЩАЮ
Одним из первых ученых, отчетливо представлявших себе ожидаемую ценность, был Блез Паскаль. Пытаясь найти ответ на вопросы, которые поставил ему любитель азартных игр Антуан Гомбо (называвший себя кавалером де Мере), Паскаль потратил вторую половину 1654 года на переписку с Пьером Ферма, пытаясь понять, какие ставки в случае многократного повторения принесут прибыль в долгосрочной перспективе, а какие приведут к разорению. Если говорить в современных терминах, он хотел понять, какие ставки имеют положительную ожидаемую ценность, а какие отрицательную. Принято считать, что эта переписка между Паскалем и Ферма положила начало теории вероятностей.
Вечером 23 ноября 1654 года Паскаль, уже после своего обращения в веру, пережил сильный мистический опыт, который изложил так, как мог:
Огонь
Бог Авраама, Бог Исаака, Бог Иакова, а не Бог философов и ученых.
…
Я был с Ним разлучен. Я бежал, отрекся от Него, я Его распял.
Да не разлучусь с Ним никогда.
Его хранят лишь на путях, указанных в Евангелии.
Полное и кроткое отречение.
…
Полная покорность Иисусу Христу и моему духовнику.
Вечная радость за день испытаний на земле.

Рукопись «Мемориала», выполненная на пергаменте. Фотография © Bibliothèque Nationale de France, Paris
Паскаль зашил страницу с этими строками в полу камзола и хранил ее там до конца своих дней. После этой «ночи огня» Паскаль оставил занятия математикой, посвятив все свои интеллектуальные усилия религиозным темам. В 1660 году, когда его старый друг Пьер Ферма написал письмо с предложением встретиться, Паскаль ответил:
Сказать вам откровенно, я считаю математику самым возвышенным упражнением для ума; но в то же время я нахожу ее столь бесполезной, что не вижу большой разницы между человеком, который всего лишь математик, и искусным ремесленником. Да, я называю ее прекраснейшим ремеслом на свете; но, в конце концов, это не более чем ремесло. <…> Но теперь у меня к этому добавляется еще и то, что я погружен в занятия, столь далекие от таких вещей, что едва помню об их существовании .
Паскаль умер через два года, в возрасте тридцати девяти лет, оставив после себя множество записей и коротких эссе, предназначенных для книги в защиту христианства. Впоследствии все эти материалы были собраны в книге Pensées («Мысли»), опубликованной через восемь лет после смерти Паскаля. Это поразительная работа, которая изобилует афоризмами и которую можно цитировать бесконечно, во многом наполненная отчаянием и во многом непостижимая. Большая часть паскалевских «Мыслей» содержит короткие пронумерованные фрагменты, представляющие собой вспышки мысли:
(434)199. Представьте себе цепочку людей в кандалах. Все они приговорены к смерти, и каждый день кого-то из них казнят на глазах у других; оставшиеся в живых видят свою судьбу в судьбе себе подобных и, глядя друг на друга с мукой и без надежды, ожидают, когда настанет их черед. Вот образ удела человеческого.
(361)209. Разве ты не остаешься рабом, когда господин тебя любит и ласкает? Ты на верху блаженства, раб, господин тебя обласкал. Он тебя скоро побьет.
Однако самый известный фрагмент «Мыслей» Паскаля — параграф двести тридцать третий, названный им Infinite-rien («Бесконечное ничто»), широко известный как «Пари Паскаля».
Как мы уже говорили в предыдущей главе, Паскаль считал вопрос о существовании Бога неподвластным логике: «Бог или есть, или Его нет; но на какую сторону мы склонимся? Разум тут ничего определить не может». Однако Паскаль на этом не останавливается. Что такое вопрос веры, спрашивает он, если не азартная игра, игра с максимально возможными ставками, игра, в которую вы не можете не играть? Анализ ставок, проведение различия между разумной и глупой игрой — это была тема, которую Паскаль понимал лучше всех на свете. По большому счету, он не совсем забросил математическую работу.
Как Паскаль вычисляет ожидаемую ценность игры в веру? Ключ к этому содержится в его «Мемориале» — мистическом откровении:
Вечная радость за день испытаний на земле.
Что это, если не вычисление издержек и выгод принятия веры? Даже в разгар экстатического общения со спасителем Паскаль делал математические вычисления! Меня восхищает это его качество.
Чтобы вычислить ожидаемую ценность, о которой говорил Паскаль, нам необходимо знать вероятность существования Бога. Представим себе на мгновение, что мы глубоко сомневаемся в этом, и присвоим данной гипотезе вероятность в размере всего 5%. Если мы верим в Бога и окажемся правы, тогда наше вознаграждение — «вечная радость», или, если говорить в экономических терминах, бесконечно большое количество ютилей. Если мы верим в Бога и окажемся неправы (результат, в котором мы уверены на 95%), тогда мы заплатим за это свою цену; может быть, даже нечто большее, чем «один день исполнения долга на земле», как предположил Паскаль, поскольку мы должны учесть не только время, потраченное на выполнение религиозных обрядов, но и ценность тех мирских удовольствий, которые мы упустили в поисках спасения. Тем не менее это фиксированная сумма, скажем, сто ютилей.
В таком случае ожидаемая ценность веры равна:
(5%) × бесконечность + (95%) (−100).
Итак, 5% — это малая величина, однако бесконечная радость — очень много радости, а значит, 5% от этого количества по-прежнему представляют собой бесконечную величину. Следовательно, эта бесконечная радость захлестнет нас, чего бы нам ни стоило принятие религии.
Мы уже говорили об опасности попыток присвоить ту или иную числовую вероятность такой гипотезе, как «Бог есть». Непонятно, имеет ли вообще какой-то смысл такое присвоение вероятности. Однако Паскаль вообще не предпринимает никаких рискованных действий с числами. Ему это не нужно, поскольку не играет роли, какое это число — 5% или какое-то другое. Один процент от бесконечного блаженства — это все то же бесконечное блаженство, превосходящее любые конечные издержки, которые влечет за собой жизнь в добродетели. Это можно сказать о величине 0,1% или 0,000001%. Важно только одно: что вероятность существования Бога не равна нулю. Разве вы не должны согласиться с этой мыслью? Что существование Бога как минимум возможно? Если да, то вычисление ожидаемой ценности дает однозначный результат: верить стоит. Ожидаемая ценность такого выбора — это не просто положительная, а бесконечно положительная величина.
У аргументации Паскаля есть серьезные недостатки. Самый большой из них заключается в наличии той же проблемы «Кота в шляпе», о которой мы говорили в : Паскаль не смог проанализировать все возможные гипотезы. В его схеме существует всего два варианта: что христианский Бог действительно существует и вознаградит определенную группу верующих, или что Бога нет. Но что если существует Бог, который вовеки проклинает христиан? Разумеется, такой Бог тоже возможен, и одной только этой возможности достаточно, чтобы уничтожить аргумент Паскаля: теперь, приняв христианство, мы рассчитываем на возможность бесконечной радости, но при этом оказываемся под угрозой бесконечных мучений, и у нас нет надежного способа взвесить относительную вероятность этих двух вариантов. Мы вернулись к тому, что разум ничего решить не может.
Вольтер выдвинул другое возражение. Возможно, вам казалось, что он должен одобрительно относиться к пари Паскаля: как мы уже видели, он не имел ничего против азартных игр. Вольтер любил математику; его отношение к Ньютону граничило с поклонением (однажды он назвал его Богом, которого он почитает). Кроме того, на протяжении многих лет Вольтер поддерживал романтические отношения с математиком Эмили дю Шатле. Однако Паскаль не относился к числу мыслителей, которыми Вольтер восхищался. Между этими двумя людьми были огромные разногласия как личностного, так и философского характера. В жизнеутверждающем мировоззрении Вольтера не было места мрачным, мистическим всплескам мысли погруженного в себя Паскаля. Он называл Паскаля «возвышенным мизантропом» и посвятил длинное эссе опровержению «Мыслей» — одного фрагмента за другим . Вольтер относился к Паскалю как признанный умница и всеми обласканное дитя к вечно унылому, ни во что не вписывающемуся зануде.
Что касается так называемого пари из параграфа 233, то Вольтер считал его «немного неприличным и ребяческим; эта идея игры, выигрыша и проигрыша не подобает серьезности предмета. …Более того, моя заинтересованность в том, чтобы во что-то верить, не является доказательством существования этой вещи». Сам Вольтер, будучи человеком жизнерадостным, склоняется к неформальному аргументу о замысле: посмотрите на этот мир, посмотрите, как он прекрасен, а значит, Бог есть, что и требовалось доказать!
Однако Вольтер не понял главного. Интересно то, что пари Паскаля звучит весьма современно — настолько современно, что Вольтер просто не уловил суть. Вольтер прав в том, что, в отличие от Вицтума и других искателей библейских кодов, или Арбетнота, или современных сторонников теории разумного замысла, Паскаль не предлагает никаких доказательств существования Бога. На самом деле он говорит только о причине для веры, но эта причина должна быть связана с полезностью веры, а не с ее обоснованием. В каком-то смысле Паскаль предвосхищает суровую позицию Неймана и Пирсона, о которой шла речь в . Как и они, он скептически относился к идее, что доказательства, с которыми мы сталкиваемся, откроют перед нами надежный способ определения, что является истинным. Однако нам не остается ничего другого, как решать, что делать. Паскаль не пытается убедить вас в том, что Бог есть; он пытается донести до вас мысль, что вам выгодно верить в это, а значит, ваш лучший курс действий — общаться с христианами и демонстрировать благочестие в разных его формах до тех пор, пока в силу самой близости с верующими вы сами не начнете по-настоящему верить. Могу ли я сформулировать аргументацию Паскаля на современном языке лучше, чем это сделал Дэвид Фостер Уоллес в романе Infinite Jest («Бесконечная шутка»)? Нет, не могу.
Отчаявшихся, потерявших надежду людей, которые только что встали на путь трезвости, неизменно поощряют и призывают хотя бы на словах поддерживать лозунги, которых они еще не понимают и в которые не верят — скажем, «Медленно, но верно!», «Двигайся дальше!» или «Шаг за шагом!». Это называется «Притворяйся, пока это не станет правдой» — фраза, которая сама по себе часто используется как лозунг. Каждый, кто взял на себя Обязательство, поднимается со своего места, чтобы выступить перед другими членами группы, и начинает со слов о том, что он алкоголик, и говорит, считает ли так он сам или нет. Затем каждый из присутствующих произносит, как благодарен он за то, что сегодня трезв, а также как замечательно вместе с группой работать над выполнением Обязательства — и все это говорится даже тогда, когда человек не испытывает ни благодарности, ни удовлетворения. Вас заставляют говорить все это до тех пор, пока вы не начнете в это верить. Однажды вы спросите человека, который уже давно ведет трезвый образ жизни, сколько еще вам придется таскаться на эти треклятые собрания, а он улыбнется так, что это едва не выведет вас из себя, и скажет: пока ты не захочешь ходить на эти треклятые собрания.
САНКТ-ПЕТЕРБУРГ И ЭЛЛСБЕРГ
Ютили могут пригодиться при принятии решений по поводу того, что не имеет четко определенной денежной стоимости, например зря потраченное время или неприятная еда. Но о полезности необходимо говорить даже в тех случаях, когда речь идет о чем-то имеющем определенную денежную стоимость — скажем, о деньгах.
Осознание этого пришло еще в самом начале развития теории вероятностей. Подобно многим другим важным открытиям, эта идея впервые была сформулирована в виде головоломки. Даниил Бернулли описал ее в 1738 году, в труде Exposition on a New Theory of the Measurement of Risk («Опыт новой теории измерения жребия»):
Петр бросает вверх монету, пока она не упадет лицевой стороной вверх; если это произойдет после первого броска, он должен дать Павлу 1 дукат, но если только после второго — 2 дуката, после третьего — 4, после четвертого — 8 и так далее, так что после каждого броска число дукатов удваивается.
Очевидно, что для Павла это достаточно привлекательный сценарий игры, за участие в которой он готов выложить какую-то сумму. Но какую именно? Учитывая наш опыт с лотереями, естественный ответ сводится к тому, чтобы вычислить ожидаемую ценность суммы денег, которую Павел получит от Петра. Вероятность того, что монета упадет лицевой стороной вверх после первого же броска, составляет 50 на 50, и в этом случае Павел получит один дукат. Если после первого броска выпадет реверс, а после второго аверс (событие, которое происходит в одном из четырех случаев), Павел получит два дуката. Чтобы он получил четыре дуката, в первых трех бросках монета должна упасть так: реверс, реверс, аверс (что происходит с вероятностью 1/8). Если продолжить этот ряд и просуммировать его отдельные элементы, ожидаемая прибыль Павла составит:
(1/2) × 1 + (1/4) × 2 + (1/8) × 4 + (1/16) × 8 + (1/32) × 16 +…
или
1/2 + 1/2 + 1/2 + 1/2 +…
Данная сумма не является числом. Это расходящийся ряд: чем больше членов вы складываете, тем больше становится сумма, увеличиваясь до бесконечности и превышая любой конечный предел. На первый взгляд может показаться, что Павел готов заплатить любое количество дукатов за право принимать участие в игре.
Похоже на полную чушь. И так оно и есть! Однако, когда математика говорит, что нечто похоже на чушь, математики не уходят прочь, пожав плечами. Мы начинаем искать тот поворот, после которого либо математика, либо наша интуиция пошла не по тому пути. Эту головоломку, известную как санкт-петербургский парадокс, впервые сформулировал Николай Бернулли (двоюродный брат Даниила) примерно на тридцать лет раньше, и многие специалисты по теории вероятностей того времени ломали над ней голову, но так и не пришли к удовлетворительному выводу. Младший Бернулли предложил замечательный способ разрешения этого парадокса — важнейший результат, с тех пор лежащий в основе экономического мышления по поводу неопределенной ценности. Бернулли утверждал: было бы ошибкой говорить, что дукат — это просто дукат. Дукат в руках богатого человека имеет иную ценность, чем дукат в руках крестьянина, что можно увидеть даже по тому, насколько по-разному эти двое относятся к своим деньгам. В частности, две тысячи дукатов — это не в два раза лучше одной тысячи, поскольку для человека, у которого уже есть тысяча дукатов, тысяча дукатов имеет меньшую ценность, чем для человека, у которого нет ничего. В два раза больше дукатов не означает в два раза больше ютилей: не все линии прямые, а зависимость между деньгами и их полезностью отображается в виде одной из таких непрямых линий.
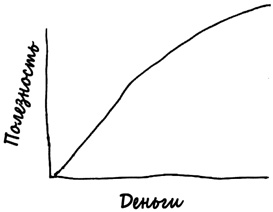
Бернулли считал, что такая полезность возрастает по логарифмическому закону, то есть k-й приз в размере 2k дукатов имеет ценность всего k ютилей. Помните: мы можем представить логарифм как своего рода совокупность цифр, а значит, если сформулировать гипотезу Бернулли в долларах, то она гласит, что богатые люди измеряют ценность своих денег в количестве цифр после долларового знака: миллиардер настолько богаче миллионера с капиталом 100 миллионов долларов, насколько миллионер с капиталом 100 миллионов долларов богаче миллионера с капиталом 10 миллионов долларов.
В формулировке Бернулли ожидаемая полезность петербургской игры представляет собой сумму:
(1/2) × 1 + (1/4) × 2 + (1/8) × 3 + (1/16) × 4 +…
Это укрощает парадокс, поскольку, оказывается, эта сумма больше не является бесконечной или даже большой. На самом деле существует замечательный прием, который позволяет нам точно вычислить эту сумму:
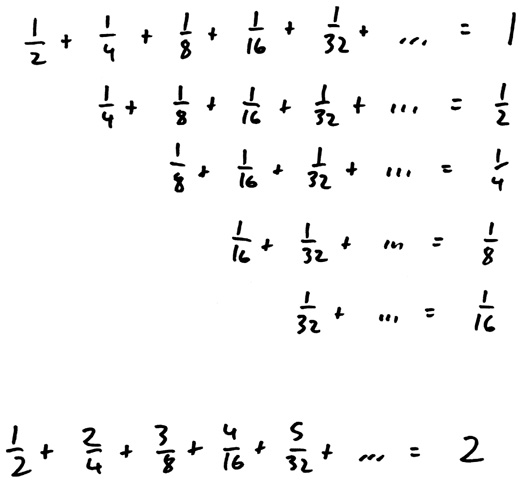
Сумма первого ряда, (1/2) + (1/4) + (1/8) + …, равна 1; это тот самый бесконечный ряд, который обнаружил Зенон в . Второй ряд такой же, как и первый, только каждый его член разделен на 2, а значит, сумма этого ряда должна быть равной половине суммы первого ряда, то есть 1/2. Точно так же третий ряд, представляющий собой второй ряд, в которой каждый член разделен на 2, должен быть равным половине суммы второго ряда, то есть 1/4. Сумма всех чисел, представленных в правой части этого треугольника, равна 1 + 1/2 + 1/4 + 1/8 + …, на единицу больше, чем сумма ряда Зенона, другими словами, 2.
Но что если мы просуммируем сначала столбцы, а не ряды? Как и в случае с отверстиями в боковой панели стереосистемы моих родителей, не имеет значения, как считать — по горизонтали или по вертикали: сумма останется одной и той же. В первом столбце есть только число 1/2; во втором два числа 1/4, то есть (1/4) × 2; в третьем три числа 1/8, то есть (1/8) × 3, и так далее. Ряд, сформированный из сумм столбцов, — это не что иное, как сумма, которую установил Бернулли для изучения санкт-петербургской задачи. А эта сумма представляет собой сумму всех чисел бесконечного треугольника, то есть 2. Следовательно, сумма денег, которую должен заплатить Павел, равна такому количеству дукатов, которое, согласно его личной кривой полезности, стоит 2 ютиля.
Помимо того факта, что кривая полезности изгибается вниз по мере увеличения количества денег, ее форму невозможно определить точно, хотя современные экономисты и психологи постоянно изобретают все более замысловатые эксперименты, призванные внести ясность в наше понимание свойств этой кривой. («А теперь, если не возражаете, удобно положите голову в центре камеры функционального магнитно-резонансного томографа, и я попрошу вас упорядочить следующие шесть покерных стратегий, от самых привлекательных до наименее привлекательных. Затем, если вы не против, полежите спокойно еще немного, пока мой ассистент возьмет у вас мазок из ротовой полости…»)
По крайней мере мы знаем, что не существует универсальной кривой: разные люди в разных ситуациях присваивают деньгам разную полезность. Это важный факт, который заставляет нас задуматься (или как минимум должен), когда мы начинаем делать обобщения по поводу экономического поведения. Грег Мэнкью — экономист Гарвардского университета, чью оценку рейганомики мы дали в , в 2008 году написал в своем блоге, что предложенное кандидатом в президенты США Бараком Обамой повышение налогов заставит его меньше работать. Ведь Мэнкью уже достиг точки равновесия, в которой полезность денег, которые он получил бы за дополнительный час работы, была бы полностью сведена на нет отрицательной полезностью потери часа времени, который он мог бы провести со своими детьми. Сократите количество денег, зарабатанных Мэнкью за один час, — и эта сделка перестает быть выгодной для него; в итоге он будет сокращать объем выполненной работы до тех пор, пока этот объем не опустится до того уровня доходов, на котором один час с детьми будет иметь для него такую же ценность, что и один час, потраченный на работу с сокращенной Обамой оплатой. Мэнкью разделяет подход Рейгана к экономике с точки зрения звезды ковбойских фильмов: когда налоговая ставка повышается, вы снимаете меньше фильмов.
Но не все рассуждают так, как Грег Мэнкью. В частности, не у всех такая же кривая полезности, как у него. Автор комических эссе Фран Лебовиц рассказывает историю своей манхэттенской молодости, когда она работала таксистом. Она начинала зарабатывать на такси в начале месяца и делала это каждый день, пока не заработает достаточно денег на жилье и еду. Затем прекращала водить такси и оставшуюся часть месяца писала. Для Фран Лебовиц все деньги, заработанные свыше определенного порога, имеют, по сути, нулевую полезность. Это означает, что у нее совсем другая кривая полезности, чем у Мэнкью. Ее кривая становится пологой, как только она расплатится за жилье. Что произойдет с Фран Лебовиц, когда повысится подоходный налог? Она будет работать больше, а не меньше, чтобы вернуться к своему пороговому значению дохода.

Бернулли был не единственным математиком, который пришел к идее полезности и ее нелинейной связи с деньгами. У него было как минимум два предшественника, одним из которых был Габриель Крамер из Женевы, а другим — не кто иной, как бросатель игл Жорж Луи Леклерк, граф де Бюффон. Интерес Бюффона к вероятности не ограничивался салонными играми. На более позднем этапе своей жизни он так вспоминал о своей встрече с досадным санкт-петербургским парадоксом:
Какое-то время я размышлял над этой задачей, но не мог определить, в чем загвоздка; я не видел возможности привести математические расчеты в соответствие со здравым смыслом без учета моральных соображений. Когда я сообщил о своих идеях господину Крамеру, он сказал мне, что я прав и что он также решил этот вопрос с помощью аналогичного подхода.
Бюффон пришел к точно такому же выводу, что и Бернулли, причем он особенно отчетливо представлял себе эту нелинейность:
Деньги не должны оцениваться по их численному количеству: если бы металл, который является всего лишь символом богатства, сам был богатством, другими словами, если бы счастье или выгоды, проистекающие из богатства, были пропорциональны количеству денег, у людей были бы основания выражать их стоимость в числовой форме и по их количеству, однако далеко не всегда бывает так, что польза денег пропорциональна их количеству: богатый человек с доходом в сотню тысяч экю не является в десять раз более счастливым, чем человек, у которого всего десять тысяч экю. Деньги представляют собой нечто большее, и как только их количество превышает определенный предел, они почти не имеют реальной ценности и не способны повысить благополучие того, кому они принадлежат: человек, обнаруживший гору золота, будет не богаче того, кто нашел всего одну кубическую морскую сажень золота.
Принцип ожидаемой полезности притягательно прямолинеен и прост: при наличии ряда вариантов следует выбирать тот вариант, который имеет максимальную ожидаемую полезность. Пожалуй, этот принцип наиболее близок к математической теории индивидуального принятия решений из всего, что у нас есть. Кроме того, модель ожидаемой полезности охватывает многие аспекты того, как люди принимают решения, поэтому она остается основным количественным инструментом среди всех тех методов, которыми пользуются социологи. Свой трактат Essai philosophique sur les probabilités («Опыт философии теории вероятностей»), написанный в 1814 году, Пьер Симон Лаплас закончил такими словами: «Мы видим в этом эссе, что теория вероятностей есть в сущности не что иное, как здравый смысл, сведенный к исчислению: она заставляет оценивать с точностью то, что рациональные умы чувствуют как бы инстинктом, часто не отдавая себе в этом отчета. …Она не оставляет места для сомнения в выборе мнений и решений; ее применение позволяет сделать самый правильный выбор».
И снова мы видим все тот же принцип: математика — это продолжение здравого смысла другими средствами.
Однако ожидаемая полезность не отвечает на все вопросы. В который раз досадные сложности предстают в виде головоломки. В данном случае головоломку сформулировал военный аналитик Дэниел Эллсберг, впоследствии получивший известность как разоблачитель нелицеприятных подробностей войны во Вьетнаме, передавший прессе секретные документы Пентагона. (В математических кругах, которые бывают порой довольно ограниченными в своих взглядах, нередко можно было услышать, как об Эллсберге говорят нечто в таком роде: «Знаете, прежде чем заняться политикой, он делал поистине важную работу».)
За десять лет до своей внезапной известности, в 1961 году, Эллсберг был блестящим молодым аналитиком в корпорации RAND, консультировавшим правительство США по вопросам ядерной войны: как можно ее предотвратить, а если это невозможно, то как эффективно вести. Одновременно с этим он работал над своей докторской диссертацией по экономике в Гарвардском университете. В обеих областях своей деятельности Эллсберг много размышлял о процессе принятия решений в условиях неизвестности. В то время теория ожидаемой полезности занимала важнейшее место в математическом анализе решений. В своей фундаментальной книге Theory of Games and Economic Behavior («Теория игр и экономическое поведение») Фон Нейман и Моргенштерн доказали, что все люди, подчиняющиеся определенному набору правил поведения, или аксиом, должны действовать так, будто их решения ориентированы на максимизацию функции полезности. Эти аксиомы (которые впоследствии определил Леонард Джимми Сэвидж, входивший в состав Группы статистических исследований вместе с Абрахамом Вальдом) были в то время стандартной моделью поведения в условиях неопределенности.
Теория игр и теория ожидаемой полезности до сих пор играют большую роль в изучении переговоров между людьми и государствами, но никогда эта роль не была такой важной, как в RAND в разгар холодной войны, где к трудам фон Неймана и Моргенштерна относились с таким же благоговением и анализировали так же тщательно, как Пятикнижие. Исследователи RAND изучали основополагающие аспекты человеческой жизни, а именно: проблему выбора и вопросы конкуренции. А в играх, которые они исследовали (таких как пари Паскаля), были очень высокие ставки.
Эллсберг, будучи молодым талантливым ученым, имел склонность выходить за рамки общепринятых ожиданий. Закончив Гарвардский университет третьим в своей группе, он поразил своих интеллектуальных собратьев тем, что записался в корпус морской пехоты, где прослужил три года в качестве рядового. Будучи еще младшим научным сотрудником, в 1959 году, Эллсберг прочитал в публичной библиотеке Бостона лекцию по стратегии внешней политики, в которой, как известно, рассуждал об эффективности действий Адольфа Гитлера в качестве геополитического стратега: «Это мастер своего дела, действия которого следует изучить, с тем чтобы узнать, на что можно рассчитывать, что можно сделать в случае угрозы насилия». (Эллсберг всегда настаивал на том, что он не рекомендовал Соединенным Штатам использовать гитлеровские стратегии, а хотел только беспристрастно исследовать их эффективность. Может быть, так и было, однако трудно усомниться в том, что он пытался спровоцировать аудиторию.)
Таким образом, вряд ли стоит удивляться тому, что Эллсберг не очень охотно принимал общепринятые взгляды. Еще в период работы над дипломным проектом в университете он ставил под сомнение основные положения теории игр. А в RAND он разработал знаменитый эксперимент, получивший известность как парадокс Эллсберга.
Предположим, у вас есть урна, внутри которой находится 90 шаров. Вам известно, что 30 из этих шаров красные, а про остальные 60 шаров вы знаете только то, что некоторые из них черные, а некоторые желтые. Ведущий эксперимента предлагает вам следующие четыре варианта действий.
Красный. Вы получите 100 долларов, если следующий шар, который будет вынут из урны, окажется красным; в противном случае вы не получите ничего.
Черный. Вы получите 100 долларов, если следующий шар окажется черным; в противном случае вы не получите ничего.
Не красный. Вы получите 100 долларов, если следующий шар будет либо черным, либо желтым; в противном случае вы не получите ничего.
Не черный. Вы получите 100 долларов, если следующий шар будет либо красным, либо желтым; в противном случае вы не получите ничего.
Какой вариант вы выберете — «красный» или «черный»? А как насчет «не красный» или «не черный»?
Эллсберг предлагал участникам эксперимента определить, какому варианту они отдали бы предпочтение, если у них был бы такой выбор. В итоге он обнаружил, что люди, принимавшие участие в эксперименте, чаще склонны выбирать вариант «красный», чем вариант «черный». В случае варианта «красный» вам известно, чего вы можете ожидать: у вас есть один шанс из трех получить деньги. В случае варианта «черный» вы не имеете никакого представления о том, что можно ожидать. Что касается вариантов «не красный» и «не черный», участники эксперимента Эллсберга чаще выбирали вариант «не красный», предпочитая знать, что вероятность получения награды составляет ровно 2/3.
А теперь предположим, что вам предстоит принять более сложное решение: выбрать два варианта из всех возможных, причем не по своему усмотрению, а либо «красный» и «не красный», либо «черный» и «не черный». Если вы предпочитаете вариант «красный» варианту «черный» и вариант «не красный» варианту «не черный», для вас имеет смысл выбрать вариант «красный» и «не красный» вместо варианта «черный» и «не черный».
Но здесь возникает проблема. Выбрать вариант «красный» и «не красный» — все равно что дать себе 100 долларов. Но то же самое происходит и в случае выбора варианта «черный» и «не черный»! Как одно может быть предпочтительнее другого, если это одно и то же?
Приверженцам теории ожидаемой полезности выводы Эллсберга казались очень странными. Каждый вариант должен иметь ценность, равную определенному количеству ютилей, и если вариант «красный» имеет более высокую полезность, чем вариант «черный», а вариант «не красный» — более высокую полезность, чем вариант «не черный», значит, вариант «красный» + «не красный» стоит больше ютилей, чем «черный» + «не черный», а ведь они одинаковые. Если вы хотите доверять ютилям, тогда вам придется сделать вывод о том, что участники эксперимента Эллсберга просто ошибаются в своих предпочтениях, что они не умеют делать расчеты, не поняли сути вопроса или просто сошли с ума. Однако, поскольку на самом деле среди приглашенных Эллсбергом людей были известные экономисты и специалисты по теории принятия решений, такой вывод создает ряд собственных проблем в сложившейся ситуации.
С точки зрения Эллсберга, этот парадокс объясняется ошибочностью теории ожидаемой ценности. Как скажет впоследствии Дональд Рамсфельд, есть известное неизвестное и есть неизвестное неизвестное, и с ними необходимо вести себя по-разному. «Известное неизвестное» подобно варианту «красный»: мы не знаем, какой шар будет вынут, но можем определить вероятность, что это будет шар нужного нам цвета. С другой стороны, вариант «черный» подвергает игрока воздействию «неизвестного неизвестного»: мы не только не уверены в том, что шар будет черным, но и не знаем, какова вероятность того, что он окажется черным. В книгах по теории принятия решений первый тип неизвестного называется риском, а второй неопределенностью. Рискованные стратегии поддаются количественному анализу; неопределенные стратегии, по мнению Эллсберга, выходят за пределы формального математического анализа или как минимум за пределы того математического анализа, которым занимались в корпорации RAND.
Однако ничто из сказанного выше не опровергает чрезвычайную полезность теории полезности. Существует множество ситуаций (одна из них — лотерея), и в них вся тайна, с которой мы сталкиваемся, связана с риском, который подчиняется точно определенным вероятностям. Тем не менее есть намного больше ситуаций, в которых «неизвестное неизвестное» присутствует, но играет не столь важную роль. Мы видим здесь своего рода перетягивание каната в математическом подходе к науке. Математики вроде Бернулли и фон Неймана создают формальные математические модели, проливающие свет на область исследований, понимание которой носило прежде расплывчатый характер. Ученые, подобные Эллсбергу, более свободно обращающиеся с математическими концепциями, стремятся понять пределы таких формальных математических моделей и по возможности усовершенствовать их, а если это невозможно — оставить сформулированные в категорических выражениях предупредительные знаки.
Работа Эллсберга написана в ярком художественном стиле, не свойственном формальной экономике. В заключительной части он пишет об участниках эксперимента следующее:
Байесовский подход и подход Сэвиджа дают ошибочные прогнозы и, по их мнению, плохие советы. Они сознательно, без всяких оправданий предпринимают действия, противоречащие этим аксиомам, поскольку такое поведение кажется им разумным. Неужели они ошибаются?
В Вашингтоне и корпорации RAND периода холодной войны теория принятия решений и теория игр считались высшей интеллектуальной ценностью и рассматривались в качестве научных инструментов, которые помогут выиграть следующую мировую войну, подобно тому как атомная бомба выиграла последнюю. Тот факт, что на самом деле эти инструменты могут иметь ограниченную область применения, особенно в ситуациях, у которых еще не было прецедентов, а значит, нет способа оценить вероятность (скажем, как в случае мгновенного превращения человечества в радиоактивную пыль), должен был вызывать определенное беспокойство у Эллсберга. Может быть, именно с этого, помимо разногласий насчет математики, начались его сомнения в военной системе?

