ГЛАВА ДЕВЯТАЯ
МЕЖДУНАРОДНЫЙ ЖУРНАЛ ГАРУСПИЦИИ
Вот притча, которую я узнал от статистика по имени Козма Шализи. Представьте, что вы гаруспик, то есть человек, который предсказывает будущие события по внутренностям принесенных в жертву овец, особенно тщательно подвергается анализу их печень. Безусловно, вы не считаете свои предсказания надежными только потому, что придерживаетесь практики, предписанной этрусскими божествами. Это было бы нелепо. Вам нужны доказательства. Поэтому вы и ваши коллеги отправляете материалы своей работы в рецензируемый журнал под названием «Международный журнал гаруспиции», чьи правила требуют, чтобы все без исключения опубликованные результаты прошли проверку на статистическую значимость.
Гаруспиция, особенно научно обоснованная, подкрепленная фактами, — не слишком легкое занятие. Во-первых, вы проводите много времени, пачкаясь в крови и желчи. Во-вторых, многие из ваших экспериментов не дают требуемых результатов. Вы пытаетесь использовать внутренности овцы для того, чтобы предсказать цену акций Apple, — и терпите неудачу; пытаетесь смоделировать долю голосов, которые отдадут за демократов выходцы из Латинской Америки, — и получаете неверный результат; пытаетесь оценить глобальный уровень предложения нефти — и снова терпите неудачу. Боги весьма своенравны, поэтому не всегда можно точно определить, какое расположение внутренних органов и какие именно заклинания позволят достоверно раскрыть будущее. Иногда разные гаруспики проводят один и тот же эксперимент, который одному обеспечивает нужный результат, а другому нет — кто знает, почему? Все это приводит в уныние. Порой вам хочется все бросить и поступить в юридическую школу.
Однако занятие гаруспицией того стоит — благодаря тем моментам открытия, когда все работает, и вы видите, что текстура и выступы на печени действительно предсказывают тяжелую эпидемию гриппа следующей зимой. И вы, молча поблагодарив богов, публикуете результаты своей работы.
Возможно, вы обнаружите, что это происходит в одном случае из двадцати.
При любых условиях именно на это рассчитывал бы я сам. Поскольку, в отличие от вас, я не верю в гаруспицию. Я считаю, что внутренности овцы ничего не знают о гриппе, а когда данные совпадают, это просто дело случая. Иначе говоря, во всем, касающемся гадания на внутренностях животных, я сторонник нулевой гипотезы. Поэтому в моем мире успешное завершение любого эксперимента с гаруспицией весьма маловероятно.
Насколько маловероятно? Стандартный порог статистической значимости, а значит, и критерий для публикации статьи в «Международном журнале гаруспиции» по соглашению установлен в виде p-значения, равного 0,05, или 1 из 20. Вспомните определение p-значения, которое состоит в том, что, если нулевая гипотеза истинна в случае определенного эксперимента, вероятность того, что этот эксперимент все-таки приведет к получению статистически значимого результата, составляет всего 1 из 20. Если нулевая гипотеза всегда истинна (другими словами, если гаруспиция — это надувательство в чистом виде), тогда результаты только одного из двадцати экспериментов могут быть опубликованными.
Тем не менее существуют сотни гаруспиков и тысячи овец со вспоротыми животами; при этом даже одна двадцатая предсказаний дает достаточно материала для заполнения каждого выпуска журнала новыми результатами, демонстрирующими эффективность этой методики и мудрость богов. Протокол эксперимента, который в одном случае сработал и публикуется в журнале, как правило, не дает нужных результатов, когда его пытается применить другой гаруспик. Однако материалы о проведении экспериментов, не обеспечивших статистически значимые результаты, не публикуются, поэтому никто так и не узнает о неудачных попытках воспроизвести этот эксперимент. И даже если начинают распространяться слухи, всегда есть мелкие различия, на которые могут указать эксперты, чтобы объяснить, почему последующие исследования завершились неудачей. В конце концов, мы ведь знаем, что протокол работает, поскольку проверили его и определили, что он обеспечивает статистически значимые результаты!
Современная медицина и социология — отнюдь не гаруспиция. Тем не менее в последние годы многие ученые все громче бьют тревогу: возможно, в науке гораздо больше данных, полученных в духе гадания на внутренностях животных, чем нам хотелось бы признавать.
Громче всех заявил об этом Джон Иоаннидис; в средней школе, в Греции, он блистал как математик, но впоследствии занялся медико-биологическими исследованиями. В 2005 году Иоаннидис опубликовал статью Why Most Published Research Findings Are False («Почему большинство публикуемых открытий оказываются ошибочными»), вызвавшую в медицинской среде волну жесткой самокритики, а затем вторую волну самозащиты. Мы знаем работы, привлекающие к себе внимание скорее своими сенсационными заголовками, а не собственно содержанием, — но только не в данном случае. Иоаннидис весьма серьезно подходит к идее о том, что целые области медицинских исследований относятся к категории «нулевых областей» (такие как гаруспиция), в которых просто нет фактического воздействия, поддающегося обнаружению. «Можно доказать, что выводы самых востребованных исследований являются ошибочными», — пишет Иоаннидис.
«Доказать» — это несколько больше, чем я готов принять, однако Иоаннидис все же приводит веские доводы в пользу того, что его радикальное утверждение нельзя назвать неправдоподобным. Вот в чем суть истории. В медицине большинство случаев вмешательства, которое мы предпринимаем, не обеспечивает требуемых результатов, а большинство связей, которые мы пытаемся обнаружить, отсутствуют. Возьмем хотя бы связь генов с заболеваниями: геном содержит множество генов, и большинство из них не вызывают рака, или депрессии, или ожирения, или любого другого прямого воздействия, которое можно было бы распознать. Иоаннидис предлагает нам проанализировать случай влияния генов на шизофрению. Такое влияние почти наверняка существует, учитывая, что нам известно о наследственности этого расстройства. Но где находится источник самого влияния в геноме? Исследователи могут забросить большую сеть (ведь сейчас Эпоха Больших Данных) и проанализировать сотни тысяч генов (точнее говоря, генетических полиморфизмов), чтобы выяснить, какие гены связаны с шизофренией. Иоаннидис считает, что около десяти генов действительно могут оказывать клинически значимое воздействие на возникновение этой болезни.
А как насчет оставшихся 99 990 полиморфизмов? Они не имеют никакого отношения к шизофрении. Тем не менее один из двадцати полиморфизмов, или около пяти тысяч, могут пройти проверку статистической значимости, превысив p-значение. Другими словами, среди результатов типа «Боже мой, я нашел ген шизофрении», которые могут быть опубликованы, в пятьсот раз больше фиктивных, чем реальных.
И все это при условии, что тест пройдут все гены, действительно оказывающие воздействие на возникновение шизофрении! Как мы видели в случаях с Шекспиром и баскетболом, реальное воздействие вполне может быть отброшено как статистически незначимое, если исследование недостаточно мощное, чтобы это воздействие обнаружить. Если исследования недостаточно мощные, полиморфизмы, которые действительно имеют отношение к данной болезни, могут пройти проверку значимости только в половине случаев, однако это означает, что из всех полиморфизмов, влияние которых на шизофрению подтверждено p-значением, только пять действительно оказывают такое воздействие, в отличие от пяти тысяч претендентов, прошедших проверку значимости совершенно случайно.
Хороший способ отследить соответствующие величины сводится к тому, чтобы нарисовать круги в клетках матрицы.
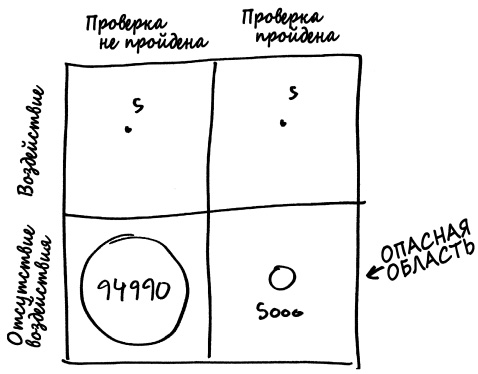
Размер каждого круга отображает количество генов в каждой категории. В левой части матрицы находятся отрицательные результаты, или полиморфизмы, которые не прошли проверку значимости, а в правой части — положительные результаты. Две верхние клетки матрицы содержат крохотное множество полиморфизмов, которые действительно связаны с шизофренией: полиморфизмы в правой верхней клетке представляют собой истинные положительные результаты (гены, связанные с шизофренией, и тест подтверждает это), тогда как в левой верхней клетке расположены ложные отрицательные результаты (полиморфизмы, связанные с шизофренией, но тест говорит о том, что это не так). В нижней части матрицы находятся полиморфизмы, не связанные с этим заболеванием: истинные отрицательные результаты представлены большим кругом в нижней левой клетке, а ложные положительные результаты — кружком в нижней правой клетке.
На этом рисунке вы можете увидеть, что сама проверка статистической значимости не является проблемой: тест выполняет именно ту работу, для которой он создан. Полиморфизмы, не имеющие никакого отношения к шизофрении, редко проходят эту проверку, тогда как полиморфизмы, действительно нас интересующие, проходят проверку в половине случаев. Однако неактивные полиморфизмы имеют большое количественное преимущество, и хотя круг ложных положительных результатов достаточно мал по сравнению с истинными отрицательными результатами, он все-таки гораздо больше круга истинных положительных результатов.
ДОКТОР, МНЕ БОЛЬНО, КОГДА Я ДЕЛАЮ Р-Р
И это только цветочки. Недостаточно мощное исследование способно обнаружить лишь довольно большое воздействие. Однако в некоторых случаях вам известно, что такое воздействие (если оно существует) совсем небольшое. Другими словами, результат исследования, которое точно оценивает воздействие того или иного гена, скорее всего будет отброшен как статистически незначимый, тогда как любой результат, прошедший тест p < 0,05, является либо ложным положительным, либо истинным положительным результатом, что значительно преувеличивает воздействие данного гена. Низкая мощность исследования особенно опасна в областях, в которых часто используются небольшие исследования, а размер воздействия, как правило, совсем небольшой. Не так давно в самом авторитетном журнале по психологии Psychological Science была опубликована статья, в которой сказано, что замужние женщины с гораздо большей вероятностью поддерживают кандидата на пост президента США от Республиканской партии Митта Ромни в благоприятный для зачатия период овуляторного цикла: из всех женщин, опрошенных в самый благоприятный для зачатия период, 40,4% женщин высказались в поддержку Ромни, тогда как всего 23,4% замужних женщин, опрошенных в неблагоприятные для зачатия периоды, отдали свои голоса за Митта. В данном случае выборка маленькая (всего 228 женщин), а различие между результатами большое — достаточно большое, чтобы пройти тест на p-значение, получив оценку 0,03.
В этом и состоит проблема: различие слишком большое. Действительно ли возможно, что среди всех состоящих в браке женщин, испытывающих симпатию к Митту Ромни, почти половина на протяжении большой части месяца поддерживают Барака Обаму? Неужели этого никто не заметил бы?
Если даже политический поворот в сторону правых во время овуляции действительно существует, то он, по-видимому, существенно меньше. Однако сравнительно небольшой размер исследуемой выборки означает, что, как ни парадоксально, более реалистичная оценка воздействия будет отброшена фильтром p-значения. Другими словами, мы можем быть вполне уверены, что значительное воздействие, о котором свидетельствуют результаты исследования, — это главным образом или всецело всего лишь шум в сигнале.
Однако этот шум с одинаковой вероятностью может направить вас в сторону, противоположную реальному воздействию, а может сказать правду. В итоге мы остаемся в неведении, получив результат, имеющий высокую статистическую значимость, но весьма низкую достоверность.
Ученые называют эту проблему «проклятие победителя», и это одна из причин, почему при повторном проведении того же опыта впечатляющие, громко расхваливаемые результаты экспериментов зачастую тают, превращаясь в удручающую лужицу. В одном показательном случае группа ученых под руководством Кристофера Шабри изучала тринадцать одиночных нуклеотидных полиморфизмов (single-nucleotide polymorphism, далее по тексту — SNP) в геноме, которые в предыдущих исследованиях показали статистически значимую корреляцию с показателем IQ. Нам известно, что способность успешно проходить тесты на определение коэффициента интеллекта в какой-то мере передается по наследству, поэтому поиск генетических маркеров не лишен оснований. Однако, когда команда Шабри проверила эти SNP на предмет корреляции с показателями IQ на больших множествах данных (таких как данные висконсинского лонгитюдного исследования, охватившего 10 тысяч человек), все эти связи оказались статистически незначимыми: если такие связи и существуют, они почти наверняка настолько слабые, что их невозможно обнаружить даже в ходе крупного эксперимента. В наше время специалисты по геномике считают, что наследственный компонент IQ, по всей вероятности, не сосредоточен в нескольких генах «умности», а скорее, формируется как совокупность многочисленных генетических особенностей, каждая из которых оказывает малое воздействие. Это означает, что, занявшись поиском большого воздействия отдельных полиморфизмов, вы добьетесь успеха — с тем же показателем 1 из 20, что и в случае гадания по внутренностям животных.
На самом деле даже Иоаннидис не считает, что только одна из тысячи опубликованных работ безошибочна. Большинство научных исследований не сводится к произвольному блужданию по геному; они проверяют гипотезы, в отношении которых у исследователей есть основания считать, что они истинны, поэтому нижняя строка матрицы не так уж значительно преобладает над верхней строкой. Однако кризис воспроизводимости результатов исследований действительно имеет место. В 2012 году было проведено исследование, в ходе которого ученые из калифорнийской биотехнологической компании Amgen попытались воспроизвести ряд самых известных экспериментальных результатов исследований в области биологии рака (всего пятьдесят три исследования). В процессе проведения независимых испытаний они смогли воспроизвести результаты лишь шести работ.
Как такое могло произойти? Причина не в том, что специалисты по геномике и ученые, изучающие онкологические заболевания, кретины. В какой-то мере кризис воспроизводимости результатов исследований — это просто отражение того факта, что наука трудна, а большинство идей, которые у нас возникают, оказываются неправильными — даже большинство идей, которые прошли первый круг тестирования.
Однако в мире науки существуют практики, которые еще больше усугубляют кризис воспроизводимости результатов исследований, и их можно изменить. Во-первых, мы используем неправильный подход к публикации научных работ. Рассмотрим в качестве примера ситуацию, изображенную на комиксе.






Предположим, вы проверили двадцать генетических маркеров на наличие связи с тем или иным заболеванием и обнаружили, что только один результат имеет статистическую значимость p < 0,05. Будучи грамотным математиком, вы осознаете, что один успешный результат из двадцати — это в точности то, чего вы ожидали бы, если ни один из маркеров не оказывал бы никакого воздействия, и высмеяли бы ничем не обоснованный заголовок, как это пытается сделать художник, нарисовавший этот комикс.
Было бы еще больше оснований утверждать это, если вы протестировали бы тот же ген (или зеленые конфетки из желе) двадцать раз и получили статистически значимый результат только в одном случае.
Но что если двадцать типов конфеток были бы протестированы двадцать раз двадцатью разными исследовательскими группами в двадцати разных лабораториях? В девятнадцати лабораторий не обнаружено статистически значимого воздействия, поэтому исследователи не пишут научные работы по полученным результатам — кто станет публиковать сенсационную новость о том, что зеленые конфетки из желе не имеют никакого отношения к состоянию вашей кожи? Ученые из двадцатой лаборатории (везунчики) обнаруживают статистически значимое воздействие, поскольку им повезло — но они не знают, что им повезло. Все, что они могут сказать, так это то, что они всего один раз проверили гипотезу «зеленые конфетки из желе вызывают прыщи», и она прошла тест на статистическую значимость.
Если вы принимаете решение, какого цвета конфетки можно есть, только на основании опубликованных работ, вы совершаете ту же ошибку, что и армейские чиновники, которые подсчитывали пробоины только на самолетах, вернувшихся после воздушных боев. Как отметил Абрахам Вальд, если вы хотите получить правдивую картину происходящего, необходимо принять во внимание и те самолеты, которые не вернулись.
Это так называемая проблема архивного ящика: в той или иной области науки формируется крайне искаженная картина доказательств в пользу гипотезы, когда широкое распространение полученных данных ограничено порогом статистической значимости. Но мы уже дали этой проблеме другое название. Речь идет о балтиморском брокере. Везучий ученый, который взволнованно готовит публикацию по теме «Связь между зелеными конфетками из желе и дерматологическими проблемами», напоминает наивного инвестора, который отдает все свои сбережения жуликоватому брокеру. Этот инвестор, так же как и ученый, видит только результаты одного эксперимента, по воле случая завершившегося успешно, но ничего не знает о гораздо более многочисленной группе неудавшихся экспериментов.
Однако здесь есть одно существенное различие. В науке нет нечистых на руку мошенников и невинных жертв. Когда члены научного сообщества отправляют результаты неудавшихся экспериментов в архив, они играют и ту и другую роль. Они совершают мошенничество по отношению к самим себе.
И все это при условии, что ученые, о которых идет речь, ведут справедливую игру. Но так бывает не всегда. Помните проблему пространства для маневра, из-за которой попали в ловушку искатели библейских кодов? Ученые, которые вынуждены публиковать свои работы, чтобы не разрушить научной карьеры, могут не устоять перед соблазном того же пространства для маневра. Если вы проводите собственный статистический анализ и получаете p-значение 0,06, вы должны сделать вывод, что ваши результаты статистически незначимы. Однако, чтобы отправить результаты многих лет работы в архив, требуется высокая психологическая устойчивость. В конце концов, разве данные об этом конкретном участнике экспериментального исследования не выглядят несколько подозрительными? Если это резко отклоняющееся значение, может быть, стоит попытаться удалить эту строку из таблицы данных. Был ли учтен возраст? Были ли учтены погодные условия? Был ли учтен возраст и погодные условия? Если только вы позволите себе слегка подправить и завуалировать результаты статистической проверки полученных данных, во многих случаях вам удастся снизить p-значение с 0,06 до 0,04. Профессор Пенсильванского университета Ури Саймонсон, ведущий ученый в области изучения проблемы воспроизводимости результатов исследований, называет эту практику «p-хакингом» . Хакинг p-значения бывает, как правило, не таким грубым, каким я его здесь представил, и редко происходит по злому умыслу. P-хакеры искренне верят в истинность своих гипотез (как в случае искателей библейских кодов), а когда вы верите во что-то, легко обосновать, что анализ, который дает пригодное для публикации p-значение, — это именно то, что вам и следовало сделать с самого начала.
Однако все знают, что на самом деле это неправильно. Когда ученым кажется, что их никто не слышит, они говорят о своей практике: «Пытаем данные, пока они не сознаются». Следовательно, достоверность результатов соответствует тому, что можно ожидать от признаний, полученных силой.
Оценить масштаб проблемы p-хакинга не так просто: невозможно проанализировать работы, которые были отправлены в архив или вообще не были написаны, подобно тому как нельзя изучить самолеты, сбитые во время воздушых боев, чтобы найти места пробоин. Но вы, так же как Абрахам Вальд, можете сделать ряд логических выводов по поводу данных, которые не можете получить напрямую.
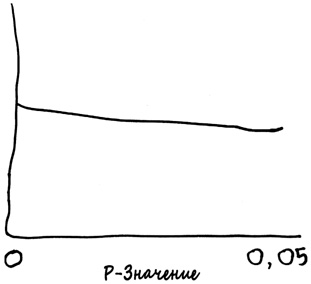
Вспомните о «Международном журнале гаруспиции». Что вы увидели бы, если могли бы изучить все когда-либо опубликованные работы и записать обнаруженные там p-значения? Не забывайте о том, что в данном случае нулевая гипотеза неизменно истинна, поскольку гаруспиция не работает. Следовательно, 5% экспериментов дадут p-значение 0,05 или меньше, 4% получат p-значение не более 0,04, 3% — не более 0,03 и так далее. Эту же идею можно сформулировать так: количество экспериментов, обеспечивающих p-значение от 0,04 до 0,05, должно быть примерно таким же, что и в случае p-значения от 0,03 до 0,04, от 0,02 до 0,03 и так далее. Если отобразить все p-значения, упомянутые во всех работах, которые вы изучили, получится такой плоский график.
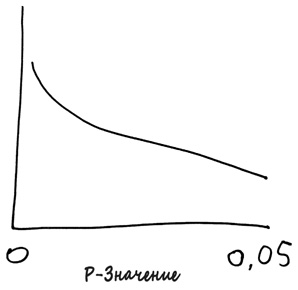
Но что если вы посмотрите реальный журнал? Хотелось бы надеяться, что многие из тех феноменов, информацию о которых вы ищете, действительно существуют; это повысит вероятность того, что эксперименты получат хорошее (а значит, низкое) p-значение. В таком случае график p-значений должен быть нисходящим.
Однако это не совсем то, что происходит в реальной жизни. В самых разных областях науки, от политологии до экономики, психологии и социологии, детективы от статистики обнаружили заметный восходящий наклон графика при приближении p-значений к порогу 0,05.
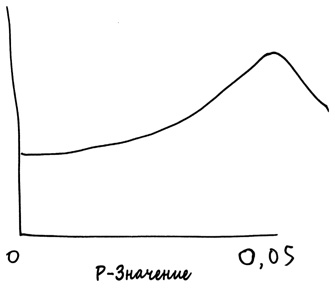
Именно этот наклон отображает факт p-хакинга. Такой график говорит о том, что результаты многих экспериментов, попадающие на ту сторону границы p = 0,05, на которой находятся не подлежащие публикации работы, посредством обмана, незначительных изменений, поправок или элементарного искажения были перенесены на более благоприятную сторону графика. Это хорошо для ученых, но плохо для науки.
Но что если автор работы отказывается истязать данные или если пытки все равно не дают требуемого результата и p-значение остается на уровне, слегка превышающем столь важный порог 0,05? В этом случае есть обходные пути. Ученые придумывают замысловатые формулировки, пытаясь оправдать получение результатов, не достигших порога статистической значимости. Они говорят, что эти результаты «почти значимы», «склоняются к значимости», «находятся на грани значимости» или даже что они «колеблются на пределе значимости». Конечно, можно было бы просто высмеять испытывающих такие муки исследователей, полагающихся на подобные фразы, но мы должны критиковать игру, а не игроков, ведь не они виновны в том, что публикация результатов их работы зависит от принципа «все или ничего». Принимать решение «жить или умереть» исключительно по значению 0,05 означало бы совершить крупную ошибку, обращаясь с непрерывной переменной (сколько у нас есть доказательств в пользу того, что лекарственный препарат работает, ген определяет IQ, а женщины в фертильный период отдают предпочтение республиканцам?) так, будто это бинарная переменная (истинный или ложный? да или нет?). Ученым необходимо дать возможность составлять отчеты о статистически незначимых данных.
В некоторых ситуациях их даже можно вынудить сделать это. Верховный суд США в 2010 году единогласно вынес решение, что Matrixx, производитель средства от простуды Zicam, обязан раскрыть информацию о том, что у некоторых пациентов, принимавших этот препарат, возникла аносмия, потеря обоняния. В этом судебном решении, которое составила Соня Сотомайор, было сказано, что, хотя данные о случаях аносмии не прошли проверку значимости, они все-таки входят в «общую совокупность» информации, на доступ к которой у инвесторов компании есть полное право. Результат с низким p-значением может представлять собой слабое доказательство, но слабое доказательство — это лучше, чем полное его отсутствие; результат с высоким р-значением мог бы стать более сильным доказательством, но, как мы уже видели, он все равно далек от подтверждения того факта, что заявленное воздействие реально.
Если уж на то пошло, в значении 0,05 нет ничего особенного. Это абсолютно произвольное значение, чистая условность, которую выбрал Фишер. Такое условное значение имеет свою ценность: благодаря единой пороговой величине, которую принимают все, мы знаем, о чем говорим, когда произносим слово «значимый». В свое время я прочитал статью Роберта Ректора и Кирка Джонсона о консервативной организации Heritage Foundation (фонд «Наследие»), которая жаловалась на ошибочное заявление конкурирующей группы ученых по поводу того, что обет воздержания не оказывает никакого воздействия на уровень распространенности заболеваний, передающихся половым путем, в подростковом возрасте. На самом деле среди принимавших участие в исследовании юношей и девушек до 20 лет, которые дали обет воздержания до первой брачной ночи, уровень распространенности заболеваний, передающихся половым путем, действительно был немного ниже, чем среди остальных членов выборки, но это различие не было статистически значимым. Представители фонда «Наследия» были в чем-то правы: доказательства того, что обет воздержания работает, были слабыми, но они все-таки были.
В то же время Ректор и Джонсон пишут в другой работе по теме статистически незначимой связи между расой и бедностью, которую они хотели бы отбросить: «Если переменная не является статистически значимой, это означает, что у этой переменной нет статистически заметной разницы между значением коэффициента и нолем, а значит, нет и воздействия». Что хорошо для трезвой гусыни, то хорошо и для перебравшего гусака! Ценность условной границы состоит в том, что она в какой-то мере дисциплинирует исследователей, удерживая их от искушения позволить собственным предпочтениям определять, какие результаты имеют значение, а какие нет.
Однако условную границу, если придерживаться ее достаточно долго, можно ошибочно принять за то, что действительно происходит в реальном мире. Представьте, что было бы, если мы говорили бы в таком духе о состоянии экономики! У экономистов есть формальное определение рецессии, которое зависит от произвольных пороговых значений, как и в случае статистической значимости. Никто не скажет: «Меня не интересует уровень безработицы, или количество строящихся жилых домов, или совокупный объем задолженности по студенческим кредитам, или дефицит федерального бюджета; если это не рецессия, мы не станем это обсуждать». Было бы глупо так говорить. Однако критики (а их с каждым годом все больше, и их голоса становятся все громче) заявляют о том, что значительная часть научной практики — это такая же глупость.
ДЕТЕКТИВ, НЕ СУДЬЯ
Очевидно, что было бы ошибкой использовать р < 0,05 в качестве синонима определения «истинный» и p > 0,05 для обозначения понятия «ложный». Доказательство от маловероятного, само по себе интуитивно привлекательное, просто не работает в качестве принципа для выведения научной истины, лежащей в основе данных.
Но какова альтернатива? Если вы когда-либо проводили эксперимент, вам известно, что научная истина не возникает из облаков, взывая к вам звуком громогласной трубы. Данные не всегда упорядочены, а логический вывод — трудный процесс.
Одна простая и распространенная стратегия сводится к тому, чтобы помимо р-значений сообщать также доверительные интервалы. Это подразумевает некоторое расширение концептуальных рамок, предлагая нам анализировать не только нулевую гипотезу, но и весь диапазон альтернатив. Предположим, у вас онлайновый магазин, который продает изготовленные кустарным способом фестонные ножницы. Будучи современным человеком (если не считать того, что вы занимаетесь изготовлением фестонных ножниц), вы устраиваете проверку «А или Б», в ходе которой половина пользователей видит текущую версию вашего веб-сайта (А), а другая половина — обновленную версию (Б) с анимационным изображением пары ножниц, которые поют и танцуют, расположившись над кнопкой «Купить сейчас». После тестирования этих двух версий сайта вы обнаруживаете, что на сайте Б объем покупок увеличивается на 10%. Отлично! Теперь, если вы человек продвинутый, у вас может возникнуть беспокойство по поводу того, не было ли это увеличение случайной флуктуацией, поэтому вы вычисляете р-значение и приходите к выводу, что вероятность получения такого хорошего результата в случае, если переформатирование сайта действительно не работало бы (то есть если нулевая гипотеза оказалась бы верной), составляет всего 0,03.
Но зачем останавливаться на этом? Если я плачу студенту колледжа за то, чтобы он сделал изображение танцующих ножниц на всех страницах моего сайта, мне нужно знать не только то, сработает ли этот прием вообще, но какие именно результаты он обеспечит. Согласуется ли воздействие, которое я обнаружил, с тем, что в долгосрочной перспективе обновление сайта повысит объем продаж всего на 5%? При такой гипотезе вы можете обнаружить, что вероятность роста на 10% гораздо выше, скажем 0,2. Другими словами, доказательство от маловероятного не исключает гипотезу, что обновление сайта приведет к улучшению ситуации на 5%. Однако вы можете оптимистично задать себе вопрос, не было ли невезение причиной полученного вами результата, и на самом деле обновление сайта повысит привлекательность ваших ножниц на 25%. Вы вычисляете еще одно р-значение и получаете 0,01 — довольно малую вероятность, которая убеждает вас отбросить эту гипотезу.
Доверительный интервал — это тот диапазон гипотез, которые доказательство от маловероятного не отбрасывают, или гипотез, которые в разумных пределах согласуются с реально наблюдаемым результатом. В данном случае доверительный интервал мог бы составлять от +3% до +17%. Тот факт, что 0%, как следовало бы из нулевой гипотезы, не включается в доверительный интервал, говорит о том, что результаты статистически значимы в том смысле, о котором шла речь выше в данной главе.
Однако доверительный интервал дает гораздо больше информации. Интервал [+3%, +17%] позволяет быть уверенным в том, что эффект положительный, но не в том, что он большой. С другой стороны, интервал [+9%, +11%] позволяет с гораздо большей уверенностью предположить, что эффект не только положительный, но и довольно большой.
Доверительный интервал содержит полезную информацию и в случаях, когда вы не получаете статистически значимых результатов — другими словами, когда доверительный интервал нулевой. Если доверительный интервал равен [−0,5%, 0,5%], тогда тот факт, что вы не получили статистически значимых результатов, становится веским доказательством в пользу того, что вмешательство не имеет никакого эффекта. Если доверительный интервал составляет [−20%, 20%], причина отсутствия статистически значимых результатов состоит в том, что вы представления не имеете, оказывает ли вмешательство какое-либо воздействие и в какую сторону. С точки зрения статистической значимости эти два следствия кажутся одинаковыми, но имеют разные последствия в плане того, чего вам следует ожидать дальше.
Разработку концепции доверительного интервала обычно приписывают Ежи Нейману, еще одному выдающемуся ученому раннего периода развития статистики. Нейман был поляком, который, как и Абрахам Вальд, занимался чистой математикой в Восточной Европе, прежде чем перейти в новую по тем временам область математической статистики и переехать на Запад. В конце 1920-х годов Нейман начал сотрудничать с Эгоном Пирсоном, унаследовавшим от своего отца Карла как академическую должность в Лондоне, так и ожесточенную научную вражду с Рональдом Фишером. Фишер был трудным человеком, всегда готовым вступить в спор; его дочь говорила о нем: «Он вырос, не научившись чутко относиться к обычным человеческим качествам собратьев». В Неймане и Пирсоне он нашел оппонентов, которые оказались достаточно непреклонными, чтобы сражаться с ним десятилетиями.
Научные разногласия между этими учеными нашли свое самое яркое выражение в подходе Неймана и Пирсона к проблеме вывода. Как установить истину по имеющимся данным? Их поразительный ответ состоит в том, чтобы не задавать вопросов. Для Неймана и Пирсона задача статистики — сказать нам, не во что нам верить, а что нам делать. Статистика ориентирована на принятие решений, а не на поиск ответов на вопросы. Проверка статистической значимости — не более чем правило, которое подсказывает ответственным лицам, целесообразно ли одобрять лекарственный препарат, предпринимать предложенную экономическую реформу или делать сайт более интересным.
Поначалу кажется просто диким отрицать тот факт, что цель науки состоит в поисках истины, но философия Неймана и Пирсона не так далека от рассуждений, которые мы используем в других областях. В чем состоит цель судебного разбирательства по уголовному делу? Мы могли бы наивно заявить, что это выяснение, действительно ли подсудимый совершил преступление, по поводу которого начато судебное разбирательство. Однако все далеко не так. Существуют нормы доказательного права, которые запрещают жюри присяжных заслушивать свидетельские показания, полученные с нарушением закона, даже если эти показания могли бы помочь им точно определить, виновен подсудимый или нет. Цель судебного разбирательства — не истина, а справедливость. У нас есть правила, которых необходимо придерживаться, поэтому, когда мы говорим, что подсудимый «виновен», мы имеем в виду (если внимательно относимся к словам) не то, что этот человек совершил преступление, в котором его обвиняют, а то, что он был осужден честно и справедливо в соответствии с данными правилами. Какие бы правила вы ни выбрали, в некоторых случаях вы неизбежно освободите преступников и посадите за решетку невиновных. Чем меньше вы делаете первое, тем больше вероятность того, что совершите второе. Поэтому мы пытаемся создавать правила, в случае которых общество так или иначе считает, что мы лучше всего обеспечиваем этот важнейший компромисс.
В понимании Неймана и Пирсона наука — тот же суд. Когда лекарственный препарат не проходит проверку значимости, мы не используем формулировку: «У нас есть уверенность, что этот препарат не работает», а говорим просто: «Не было доказано, что этот препарат работает». А затем мы отклоняем этот препарат, точно так же как прекращаем дело в отношении подсудимого, присутствие которого на месте преступления невозможно было установить в пределах разумных сомнений, даже если каждый человек в здании суда считает его виновным на все сто процентов.
Фишеру все это было не нужно: в его понимании Нейман и Пирсон погрязли в чистой математике, настаивая на строгом рационализме в ущерб всему, что напоминает научную практику. Большинство судей не пошли бы на то, чтобы позволить невиновному подсудимому встретиться с палачом, даже если того требуют существующие правила. А большинство практикующих ученых, вообще не заинтересованных в следовании строгой совокупности инструкций, отказывают себе в удовольствии выработать мнение по поводу того, какие гипотезы действительно являются истинными. В письме Уильяму Эдмунду Хику Фишер писал:
Мне немного жаль, что вы вообще беспокоились по поводу излишне серьезного подхода к проверке значимости, представленного Нейманом и Пирсоном в виде критических областей и т.д. В действительности я и мои ученики во всем мире даже не думали использовать их. Если меня попросят назвать точную причину этого, я скажу, что они подходят к проблеме совершенно не с того конца, то есть не с точки зрения исследователя, с базой обоснованных знаний, в рамках которой весьма неустойчивая совокупность гипотез и несвязанных наблюдений подвергается постоянному анализу. Что ему необходимо, так это уверенный ответ на вопрос: «Следует ли мне учитывать это?» Безусловно, этот вопрос можно и ради уточнения идеи необходимо сформулировать так: «Отбрасывает ли эта совокупность наблюдений данную гипотезу, и если да, то при каком уровне значимости?» В таком виде это можно недвусмысленно сформулировать только потому, что у настоящего экспериментатора уже есть ответы на все вопросы, на которые последователи Неймана и Пирсона пытаются (думаю, напрасно) ответить исключительно посредством математических размышлений.
Конечно, Фишер понимал, что достичь порога статистической значимости — это не то же самое, что найти истину. В 1926 году он писал и о более богатом, более итеративном подходе: «Научный факт следует считать экспериментально установленным только в случае, если должным образом спланированный эксперимент редко не обеспечивает данный уровень значимости».
Здесь сказано не «один раз обеспечивает данный уровень значимости», а «редко не обеспечивает данный уровень значимости». Статистически значимый результат дает вам подсказку по поводу того, на чем следует сосредоточить свою исследовательскую энергию. Проверка значимости — это детектив, а не судья. Вам ведь известно: когда вы читаете статью о революционном открытии по поводу того, что это вызывает то-то или что одно предотвращает другое, в конце всегда есть банальное высказывание ведущего ученого, не принимавшего участия в исследовании, который провозглашает нечто несущественное в следующем духе: «Это довольно интересное открытие, предполагающее, что необходимо провести дополнительные исследования в этом направлении»? А ведь вы даже не читаете эту часть публикации, поскольку считаете ее обязательным предостережением, не имеющим смысла.
Но дело вот в чем: ученые всегда говорят так лишь потому, что это важно и это правда! Интересное и ах-какое-статистически-значимое-открытие — это не заключительная часть научного процесса, а его начало. Если получен беспрецедентный, важный результат, другие ученые в других лабораториях должны многократно протестировать этот феномен и его варианты, пытаясь понять, является ли результат счастливой случайностью или он действительно соответствует фишеровскому стандарту «редко не обеспечивает данный уровень значимости». Это и есть то, что ученые называют воспроизводимостью: если воздействие нельзя воспроизвести, несмотря на многократные попытки, наука отступает, признавая свою ошибку. Предполагается, что такой процесс воспроизведения должен стать иммунной системой науки, которая атакует новые объекты и уничтожает те из них, которым здесь не место.
Однако это идеал. На практике у науки несколько ослабленный иммунитет. Безусловно, некоторые эксперименты трудно воспроизвести. Если задача вашего исследования состоит в том, чтобы оценить способность четырехлетних детей к отсрочке вознаграждения, а затем соотносит эти данные с итогами жизни тридцать лет спустя, вы не можете просто организовать воспроизведение эксперимента.
Но даже результаты исследований, которые можно было бы повторить, во многих случаях не воспроизводятся. Каждый журнал стремится опубликовать важное открытие, но кто хочет публиковать работу, в которой идет речь о повторении того же эксперимента год спустя с теми же результатами? Что происходит с исследованиями, в ходе которых проводятся такие же эксперименты, но полученный результат не является статистически значимым? Для того чтобы система работала, результаты этих экспериментов необходимо сделать общедоступными. Но вместо этого они слишком часто оказываются в архиве.
Однако культура меняется. Активные реформаторы, как Иоаннидис и Саймонсон, выступающие как перед научным сообществом, так и перед широкой общественностью, подняли вопрос об актуальности такой проблемы, как опасность сползания к крупномасштабному гаданию по внутренностям животных. Ассоциация психологических наук в 2013 году объявила о начале публикации новой категории статей под названием «Отчеты о зарегистрированных случаях воспроизведения результатов исследований». Способ рассмотрения отчетов об экспериментах, ориентированных на воспроизведение результатов широко известных исследований, существенно отличается от того, как рассматриваются обычные работы: материалы предложенного эксперимента принимаются к публикации до проведения самого исследования. Если результаты этого эксперимента подтверждают первоначальный вывод — отлично, если нет, они все равно публикуются, благодаря чему все научное сообщество может получить исчерпывающую информацию о фактическом положении вещей. Еще одно объединение, проект Many Labs, проводит повторную проверку открытий в области психологии, получивших широкую огласку, и пытается воспроизвести их на больших многонациональных выборках. В ноябре 2013 года психологи с воодушевлением приняли первые итоги проверки воспроизводимости, полученные Many Labs: результаты десяти из тринадцати исследований были успешно воспроизведены.
Безусловно, в конечном счете необходимо сделать окончательные выводы и подвести черту. В конце концов, что именно имел в виду Фишер под словом «редко» во фразе «редко не обеспечивает данный уровень значимости»? Присвоив этому слову произвольное числовое значение («воздействие действительно имеет место, если оно достигает статистической значимости в более чем 90% экспериментов»), мы можем снова оказаться в трудной ситуации.
Как бы там ни было, Фишер не верил в существование непреложного правила, которое говорит нам, что делать. Он не признавал чистого математического формализма. В самом конце своей жизни, в 1956 году, он писал: «В действительности ни у одного ученого нет фиксированного уровня значимости, в соответствии с которым он из года в год, при любых обстоятельствах отбрасывает гипотезы; скорее, он осмысливает каждую конкретную гипотезу в свете имеющихся доказательств и идей».

