5 Игры с одновременными ходами: непрерывные стратегии, анализ и обсуждения
В обсуждение фокусировалось на играх с одновременными ходами, в которых каждый игрок мог делать выбор из дискретного множества действий. К дискретным стратегическим играм данного типа относятся спортивные соревнования, позволяющие использовать только небольшое количество вариантов игры в заданной ситуации, скажем пенальти в футболе, когда игрок может выбирать, куда послать мяч: высоко или низко, в угол или в центр ворот. Другие примеры включают в себя координационные игры и игры под общим названием «дилемма заключенных», в которых в распоряжении игроков только две или три стратегии. Такие игры можно проанализировать с помощью таблицы игры, по крайней мере в ситуациях с приемлемым количеством участников и доступных действий.
Однако многие игры с одновременными ходами отличаются от тех, которые мы рассматривали до сих пор, тем, что их участникам приходится выбирать стратегии из широкого диапазона возможных вариантов. Игры, в которых производители выбирают цены на свои продукты, благотворители — суммы пожертвований, а подрядчики — размер заявки на участие в проекте, — все это примеры игр, в которых участники имеют практически бесконечное множество вариантов выбора. Сугубо формально цены и другие суммы в долларах все же можно выразить в минимальных единицах, таких как цент, а значит, на самом деле речь идет о конечном и дискретном множестве стратегий ценообразования. Однако на практике эта единица настолько мала, что, если бы мы допустили подобную дискретность, каждому игроку пришлось бы иметь дело с таким большим количеством дискретных стратегий, что это сделало бы таблицу игры нереально огромной. Поэтому гораздо проще и эффективнее рассматривать эти варианты выбора как непрерывно меняющиеся действительные числа. Когда у игроков столь широкий диапазон доступных действий, таблицы игр становятся фактически бесполезны в качестве инструмента анализа, оказываясь слишком громоздкими для практического применения. Для таких игр нужен иной метод решения. В первой части данной главы мы представим аналитические инструменты для решения игр с непрерывными стратегиями.
В этой главе также рассматриваются некоторые более широкие вопросы, связанные с поведением в играх с одновременными ходами и концепцией равновесия Нэша. В частности, эмпирические данные о ведении игр в соответствии с равновесием Нэша, собранные в ходе как лабораторных экспериментов, так и наблюдений за реальными жизненными ситуациями. Кроме того, представлен ряд теоретических критических замечаний в отношении концепции равновесия Нэша, а также приведены аргументы против подобной критики. Еще вы увидите, что прогнозы, составленные на основе теории игр, во многих случаях целесообразно (с некоторыми оговорками) использовать в качестве отправной точки для понимания фактического поведения.
1. Чистые стратегии, представляющие собой непрерывные переменные
В мы сформулировали метод анализа наилучших ответов для поиска всех равновесий Нэша в чистых стратегиях в играх с одновременными ходами. Теперь расширим его на игры, в которых у каждого игрока — непрерывный диапазон вариантов выбора, например при установлении компанией цен на свою продукцию. Чтобы вычислить наилучшие ответы в игре такого типа, мы должны найти для каждого возможного значения цены одной компании значение цены другой компании, которое будет для нее лучшим (максимизирует ее прибыль). Непрерывность множества стратегий позволяет нам использовать алгебраические формулы для того, чтобы продемонстрировать, как стратегии обеспечивают выигрыши, а также показать наилучшие ответы в виде линий на графике, где на осях координат отображена цена (или любая другая непрерывная стратегия) каждого из игроков. При таком способе представления игры равновесие Нэша находится в месте пересечения линий на графике. Мы разовьем эту идею и метод на примере двух историй.
А. Ценовая конкуренция
Наша первая история происходит в маленьком городке под названием Яппи-Хейвен, в котором есть два ресторана: Xavier’s Tapas Bar и Yvonne’s Bistro. Чтобы упростить ситуацию, будем исходить из предположения, что в каждом ресторане используется стандартное меню. Владельцы Xavier’s и Yvonne’s должны установить цены на блюда в своих меню; при этом цель каждого из них, чтобы эти цены обеспечивали максимальную прибыль (выигрыш в этой игре). Мы также полагаем, что рестораны печатают меню порознь, не зная о ценах друг друга, стало быть, это игра с одновременными ходами. Поскольку цены могут принимать любое значение в пределах (почти) бесконечного диапазона, начнем с введения общих или алгебраических обозначений, затем найдем правила наилучших ответов и используем их для решения игры и определения равновесных цен. Обозначим цену ресторана Xavier’s как Px а Yvonne’s как Py.
При определении цены каждый ресторан должен просчитать последствия с точки зрения прибыли. Для того чтобы упростить задачу, мы ставим два ресторана в условия симметричной зависимости, но читатели с развитыми математическими навыками могут выполнить аналогичный анализ, воспользовавшись более общими величинами или даже алгебраическими символами. Допустим, обслуживание одного клиента обходится каждому ресторатору в 8 долларов. Предположим также, что опыт или исследования рынка показывают, что, если цена ресторана Xavier’s Px, а Yvonne’s Py, количество клиентов, Qx и Qy соответственно (в сотнях клиентов в месяц) задается уравнениями
Qx = 44 – 2Px + Py,
Qy = 44 – 2Py + Px.
Основная идея этих уравнений состоит в том, что, если один ресторан повысит цену на 1 доллар (скажем, Yvonne’s повысит Py на один доллар), его объем продаж сократится на 200 в месяц (Qy уменьшится на 2), а объем продаж другого ресторана увеличится на 100 в месяц (Qx увеличится на 1). Можно предположить, что 100 клиентов ресторана Yvonne’s перейдут к Xavier’s, а еще 100 останутся дома.
Обозначим прибыль ресторана Xavier’s за неделю (в сотнях долларов в неделю) символом πх (греческая буква π [«пи»] — традиционный экономический символ для обозначения прибыли). Эта прибыль рассчитывается как произведение чистого дохода на одного клиента (цена за вычетом затрат на обслуживание, или Рх – 8) и количества обслуженных клиентов:
πx = (Px – 8)Qx = (Px – 8) (44 – 2Px + Py).
Умножив и перегруппировав члены в правой части предыдущего выражения, можем записать прибыль как функцию повышающихся степеней Рх:
πx = – 8(44 + Py) + (16 + 44 + Py) Px – 2(Px)2 = – 8(44 + Py) + (60 + Py) Px – 2(Px)2.
Xavier’s устанавливает цену Рх, чтобы максимально увеличить свой выигрыш. Делая это для каждого возможного уровня цены ресторана Yvonne’s Py, мы получим правило наилучших ответов ресторана Xavier’s, которое можно отобразить на графике.
В такой форме можно представить многие простые иллюстративные примеры, в которых одно действительное число (такое как цена) выбирается для максимального увеличения другого, зависимого от него действительного числа (например, прибыль или выигрыш). В приложении к этой главе описан простой общий метод выполнения операции максимизации; вы найдете немало случаев его применения. Здесь же мы просто приводим формулу.
Функция, которую мы хотим максимизировать, задается следующим общим уравнением:
Y = A + BX – CX2.
Мы использовали обозначение Y для величины, которую нужно максимизировать, и X для величины, которую хотим выбрать, чтобы максимизировать Y. В нашем конкретном примере прибыль πx будет представлена в виде Y, а цена Pх в виде X. Точно так же, хотя в любой конкретной задаче члены приведенного выше уравнения А, В и С были бы известны, мы обозначили их общими алгебраическими символами, с тем чтобы наша формула была применима ко множеству аналогичных задач. (Формальный термин, которым обозначаются члены А, В и С, — параметры, или алгебраические константы.) Поскольку большинство случаев практического применения подразумевают наличие неотрицательных значений X, таких как цены, а также максимизацию значения Y, необходимо, чтобы выполнялось условие В > 0 и С > 0. Тогда формула, позволяющая выбрать X для максимизации Y с учетом известных значений А, В и С, будет выглядеть так: Х = В/2С. Обратите внимание, что А в ней отсутствует, хотя это, безусловно, влияет на полученное в результате значение Y.
Сравнив общую функцию в уравнении выше и конкретный пример функции прибыли в игре в ценообразование на предыдущей странице, получим
В = 60 + Py и С = 2.
Следовательно, цена, которую выберет ресторан Xavier’s для максимального увеличения прибыли, будет удовлетворять формуле В/2С и составит
Pх = 15 + 0,25 Py.
Это уравнение определяет значение Pх, при котором прибыль ресторана Xavier’s будет максимальной при соответствующем значении цены ресторана Yvonne’s Py. Иными словами, это и есть то, что нам нужно: правило наилучшего ответа ресторана Xavier’s.
Правило наилучшего ответа ресторана Yvonne’s можно найти аналогичным способом. Поскольку затраты на обслуживание клиентов и объемы продаж двух ресторанов полностью симметричны, очевидно, что это уравнение будет иметь такой вид:
Pу = 15 + 0,25 Pх.
Оба правила используются одним и тем же способом для построения графиков наилучших ответов. Например, если Xavier’s назначит цену 16, то Yvonne’s введет это значение в свое правило наилучшего ответа, чтобы найти Pу = 15 + 0,25 (16) = 19; точно так же наилучший ответ ресторана Xavier’s на значение цены ресторана Yvonne’s Pу = 16 составляет Pх = 19, наилучший ответ каждого ресторана на цену другого 4 равен 16, на цену 8 — 17 и т. д.
На рис. 5.1 приведены графики этих двух правил наилучшего ответа. В силу особенностей нашего примера (линейная зависимость между объемом продаж и назначенными ценами, а также постоянные издержки на приготовление каждого блюда) оба графика наилучших ответов представляют собой прямые линии. При других характеристиках спроса и затрат они могут не быть прямыми линиями, но метод их построения тот же, а именно: сначала зафиксировать цену одного ресторана (скажем, Pу), а затем найти значение цены другого ресторана (например, Pх), которая максимизирует прибыль второго ресторана, и наоборот.
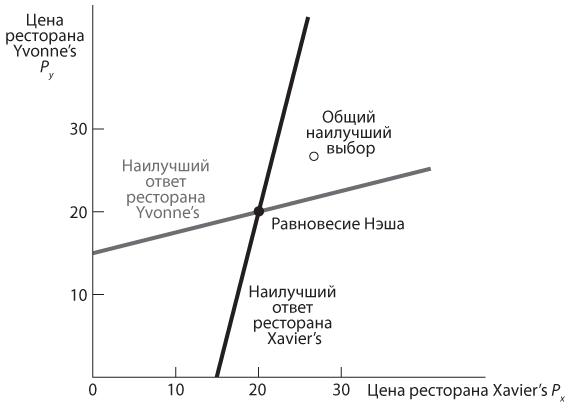
Рис. 5.1. Графики наилучших ответов и равновесия в игре «ценообразование в ресторанах»
Точка пересечения двух графиков наилучшего ответа — это равновесие Нэша в игре в ценообразование между двумя ресторанами. Она представляет пару цен (по одной на каждую компанию), которые являются наилучшими ответами друг на друга. Конкретные значения для равновесной стратегии ценообразования каждого ресторана можно вычислить алгебраически, решив два правила наилучших ответов относительно Px и Py. Мы намеренно выбрали такой пример, чтобы уравнения были линейными и легко решаемыми. В данном случае мы просто подставим формулу для Px в формулу для Py и получим следующее уравнение:
Py = 15 + 0,25Pх = 15 + 0,25(15 + 0,25Py) = 18,75 + 0,0625Py.
Последнее уравнение можно упростить до Py = 20. Ввиду симметричности задачи не составит труда найти, что Px = 20. Таким образом, в равновесном состоянии каждый ресторан назначит цену 20 долларов на блюда в своем меню и получит 12 долларов прибыли на каждых 2400 клиентов (2400 = (44 – 2 × 20 + 20) × 100), которых обслуживает за месяц, что обеспечит общий объем прибыли 28 800 долларов в месяц.
Б. Некоторые экономические аспекты олигополии
Мы привели пример с ценообразованием в ресторанах, чтобы показать, как найти равновесие Нэша в игре, где стратегии представляют собой непрерывные переменные, такие как цены. Однако эту ситуацию целесообразно проанализировать более детально и объяснить кое-какие экономические аспекты стратегий ценообразования и прибыли при конкуренции между небольшим количеством компаний (в данном случае двух). На языке экономики такую конкуренцию называют «олигополия», от греческих слов, означающих «малое количество продавцов».
Для начала обратите внимание, что график наилучшего ответа каждой компании наклонен вверх. В частности, если один ресторан поднимает цену на 1 доллар, наилучший ответ другого ресторана — поднять цену на 0,25 доллара, или 25 центов. Когда один ресторан повышает цену, некоторые его клиенты переходят в другой ресторан, а это означает, что его конкурент может получить прибыль за счет новых клиентов посредством частичного повышения цены. Таким образом, ресторан, поднимающий цену, помогает конкуренту увеличить прибыль. В случае равновесия Нэша, при котором каждый ресторан назначает цену независимо от другого и исходя исключительно из собственной прибыли, он не учитывает дополнительное преимущество, которое создает для другого ресторана. Могут ли они объединить усилия и договориться о повышении цен, тем самым увеличив свою прибыль? Да. Предположим, два ресторана установили цены по 24 доллара каждый; стало быть, каждый из них получит 16 долларов прибыли на каждого из 2000 клиентов (2000 = (44 – 2 × 24 + 24) × 100), которых ресторан обслуживает за месяц, следовательно, общий объем прибыли составит 32 000 долларов в месяц.
Эта игра в ценообразование в точности такая же, как и дилемма заключенных, рассмотренная в , но теперь стратегии носят непрерывный характер. В истории из у мужа и жены было искушение предать друг друга и признаться в совершении преступления в полиции, однако, сделав это, оба бы получили более длинные тюремные сроки (худшие исходы игры). Аналогично более прибыльная цена 24 доллара не является равновесием Нэша. Каждый из ресторанов, произведя расчеты, попытается предложить клиентам более низкую цену. Предположим, Yvonne’s начнет с цены 24 доллара. Воспользовавшись формулой наилучших ответов, можно определить, что Xavier’s при этом установит цену 15 + 0,25 × 24 = 21. Далее Yvonne’s отреагирует своим наилучшим ответом: 15 + 0,25 × 21 = 20,25. В случае продолжения этого процесса цены обоих ресторанов сведутся к равновесию Нэша, то есть к 20 долларам.
Но какая цена выгоднее для обоих ресторанов? При наличии симметрии допустим, что оба заведения назначат одну и ту же цену Р. Тогда прибыль каждого ресторана равна:
πx = πy = (P – 8) (44 – 2P + P) = (P – 8) (44 – P) = – 352 + 52P – P2.
Оба могут выбрать Р для максимизации формулы. Воспользовавшись уравнением, представленным в , мы видим, что решение: Р = 52/2 = 26. Полученная в результате прибыль каждого ресторана составит 32 400 долларов в месяц.
На языке экономики соглашение о повышении цен до уровня, оптимального для обеих сторон, называется картелем. Высокие цены наносят ущерб потребителям, поэтому органы государственного регулирования США обычно пытаются предотвратить образование картелей и заставить компании конкурировать друг с другом. Явный сговор по поводу цен находится вне закона, но негласный сговор все же может иметь место в повторяющейся дилемме заключенных (мы проанализируем повторяющиеся игры такого рода в ).
Сговор необязательно приводит к повышению цен. В нашем примере, если один ресторан снизит цену, его объем продаж увеличится отчасти потому, что он переманит некоторых клиентов от конкурента, поскольку продукты (блюда) двух ресторанов взаимозаменяемы. В других контекстах две компании могут продавать взаимодополняющие продукты, скажем программное и аппаратное обеспечение. В этом случае, если одна из них снижает цену, объем продаж в обеих компаниях возрастает. При равновесии Нэша, когда две фирмы действуют независимо друг от друга, они не учитывают выгоду, которую принесло бы обеим снижение цен. Следовательно, они поддерживают цены на более высоком уровне, чем если бы координировали свои действия. Сотрудничество между такими компаниями привело бы к снижению цен, что было бы выгодно и клиентам.
Конкуренция не всегда подразумевает использование цен в качестве стратегических переменных. Например, рыболовные флотилии могут конкурировать за более крупный улов. В таком случае имеет место конкуренция по количеству, а не по цене, рассмотренная в данном разделе. Мы опишем конкуренцию по количеству чуть ниже, а также в нескольких упражнениях, размещенных в конце главы.
В. Политическая реклама
Наш второй пример взят из политики. Он требует немного больше математических выкладок, чем мы обычно используем, но мы объясним интуитивные идеи, лежащие в их основе, с помощью слов и графиков.
Рассмотрим выборы с участием двух партий или двух кандидатов. Каждая сторона пытается отнять голоса избирателей у другой стороны посредством рекламы — либо позитивных рекламных объявлений, подчеркивающих достоинства самой партии или кандидата, либо негативной рекламы, сфокусированной на недостатках соперника. Для простоты будем исходить из предположения, что изначально избиратели не владеют никакой информацией и не отдают предпочтения ни одной из партий, поэтому формируют свое мнение исключительно под влиянием рекламы. (Многие сказали бы, что это точное описание американской политики, но более продвинутые исследования в области политологии подтверждают тот факт, что информированные, стратегически мыслящие избиратели все же существуют. Мы проанализируем их поведение более подробно в .) Для того чтобы упростить ситуацию еще больше, допустим, что доля избирателей, голосующих за партию, равна доле партии в общей сумме расходов на рекламу избирательной кампании. Назовем партии или кандидатов Л и П; если Л тратит на рекламу x миллионов долларов, а П — y миллионов долларов, то Л получит долю x / (x + y) голосов, а П — у / (x + y) голосов. Читатели, заинтересовавшиеся этой областью практического применения теории игр, найдут более общее описание соответствующих методов в специальной литературе по политологии.
Сбор средств на оплату такой рекламы требует определенных затрат; к их числу относятся деньги на рассылку писем и телефонные звонки; время и труд кандидатов, партийных лидеров и активистов; будущее политическое вознаграждение для лиц, сделавших крупные пожертвования, а также возможные политические издержки в случае, если такое вознаграждение станет достоянием гласности и повлечет за собой скандал. Для простоты анализа предположим, что все эти затраты пропорциональны прямым затратам на проведение кампании х и у. В частности, допустим, что выигрыш партии Л оценивается как процент голосов за вычетом расходов на рекламу: 100x (x + y) – x. Аналогичным образом выигрыш партии П составляет: 100у / (x + y) – у.
Теперь можем определить наилучшие ответы. Поскольку это нельзя сделать без вычислений, выведем математическую формулу, а затем объясним ее общий смысл на интуитивном уровне. Для заданной стратегии х партии Л партия П выбирает стратегию у, чтобы максимизировать свой выигрыш. Условие первого порядка можно найти, зафиксировав значение х и приравняв производную от 100у / (x + y) – у по у к нулю. В итоге получим уравнение 100x / (x + y)2 – 1 = 0, или 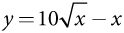 . На рис. 5.2 показан график этой функции, а также аналогичный график функции наилучшего ответа партии Л, а именно
. На рис. 5.2 показан график этой функции, а также аналогичный график функции наилучшего ответа партии Л, а именно 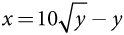 .
.
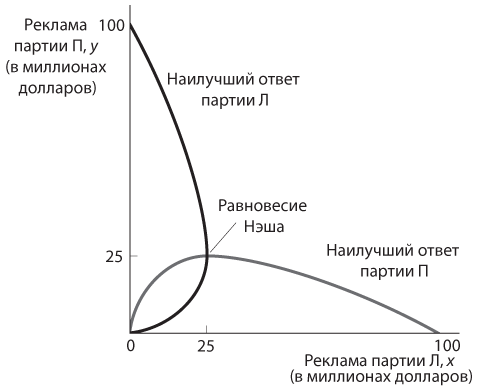
Рис. 5.2. Наилучшие ответы и равновесие Нэша в игре «политическая реклама»
Посмотрите на кривую наилучших ответов партии П. По мере роста значения переменной x партии Л значение переменной у партии П сначала немного повышается, а затем снижается. Если другая партия размещает мало рекламных материалов, то реклама первой партии обеспечит высокую отдачу в виде голосов избирателей, поэтому на незначительное увеличение расходов другой партии на рекламу целесообразно ответить еще более существенным увеличением собственных расходов на рекламу в целях усиления конкуренции. Однако если другая партия уже вкладывает в рекламу солидные средства, то реклама первой партии обеспечит мизерную отдачу по отношению к затратам на нее, поэтому лучше ответить на повышение рекламных расходов другой партии сокращением собственных расходов.
Оказывается, кривые наилучших ответов двух партий пересекаются в точках максимума. Опять же, некоторые алгебраические манипуляции с уравнениями этих двух кривых позволяют получить точные величины равновесных значений x и y. Вы можете убедиться, что в данном случае значение каждой из переменных x и y равно 25, или 25 миллионов долларов. (Предполагается, что речь идет о выборах в Конгресс; выборы в Сенат и президентские выборы обходятся в наши дни гораздо дороже.)
Как и в игре в ценообразование, здесь мы имеем дело с дилеммой заключенных. Если обе партии сократят расходы на рекламу в равной пропорции, это никак не повлияет на долю голосов избирателей, но при этом обе партии сэкономят на расходах, а значит, получат более крупный выигрыш. В отличие от картеля производителей взаимозаменяемых продуктов (который поддерживает высокие цены и наносит ущерб потребителям), соглашение между политиками о сокращении объема рекламы, по всей вероятности, принесло бы пользу избирателям и обществу в целом, подобно тому как картель производителей взаимодополняющих продуктов привел бы к снижению цен и выгоде потребителей. Из решения данной дилеммы заключенных извлекли бы пользу все. В действительности Конгресс уже несколько лет пытается это сделать и даже ввел частичные ограничения, однако политическая конкуренция слишком ожесточенная для того, чтобы обеспечить полное или длительное разрешение этой дилеммы.
Но что если партии находятся в несимметричных ситуациях? Тогда может возникнуть асимметрия двух типов. Одна партия (скажем, П) может иметь возможность размещать рекламу по более низкой цене, поскольку у нее есть доступ к средствам массовой информации. Или рекламные расходы партии П могут быть эффективнее, чем у партии Л, — например, доля голосов Л может составлять x / (x + 2y), тогда как доля голосов П — 2y / (x + 2y).
В первом случае партия П использует свой более дешевый доступ к рекламе, выбирая более высокий уровень расходов y для любого заданного значения x партии Л; иными словами, кривая наилучших ответов на смещается вверх. Равновесие Нэша смещается вверх и направо вдоль неизменной кривой наилучших ответов партии Л. Таким образом, в итоге партия П потратит на рекламу больше, а партия Л меньше, чем раньше. Это сродни ситуации, когда побеждающая сторона как будто «играет мускулами», а проигрывающая как будто сдается перед таким натиском.
Во втором случае кривые наилучших ответов обеих партий смещаются в соответствии с более сложной схемой. В итоге обе несут равные расходы на рекламу, но меньше 25, как в симметричной ситуации. В нашем примере, где эффективность рекламных расходов партии П в два раза превышает эффективность расходов партии Л, это приводит к тому, что объем расходов каждой партии составляет 200 / 9 = 22,2 < 25. (Следовательно, именно в симметричной ситуации наблюдается самая острая конкуренция.) Если рекламные расходы партии П более эффективны, верно также и то, что в связи с характером асимметричности кривых наилучших ответов новое равновесие Нэша вместо точек максимума этих двух кривых расположено на нисходящей части кривой наилучших ответов партии Л и восходящей части кривой наилучших ответов партии П. Иными словами, хотя обе партии тратят на рекламу одинаковую сумму, объем рекламных расходов партии П, находящейся в более благоприятных условиях, превышает сумму, вызывающую максимальный ответ партии Л, а объем рекламных расходов более слабой партии Л меньше суммы, способной вызвать максимальный ответ партии П. В конце данной главы приведено дополнительное упражнение (), которое позволит студентам с более высоким уровнем математических знаний вывести эти результаты.
Г. Общий метод поиска равновесий Нэша
Хотя стратегии (цены или расходы на политическую рекламу) и выигрыши (прибыль и доля голосов избирателей) в предыдущих двух примерах связаны с конкуренцией между компаниями или политическими партиями, данный метод поиска равновесия Нэша в игре с непрерывными стратегиями абсолютно универсален и вы можете использовать его для решения других подобных игр.
Предположим, игроки следуют под номерами 1, 2, 3, … . Обозначим их стратегии как х, у, z, … в этом порядке, а выигрыши — соответствующими заглавными буквами X, Y, Z, … . В общем случае выигрыш каждого игрока является функцией выбора всех игроков; отметим соответствующие функции как F, G, H, … На основании этой информации об игре составим выигрыши и запишем их так:
X = F (x, y, z, …), Y = G (x, y, z, …), Z = H (x, y, z, …).
Если использовать этот общий формат для описания нашего примера с ценовой конкуренцией между двумя игроками (компаниями), то стратегии x и y становятся ценами Px и Py. Выигрыши X и Y — это прибыль πx и πy. Функции F и G — квадратичные функции вида
πx = –8(44 + Py) + (16 + 44 + Py) Px – 2(Px)2.
Аналогичная формула есть для πy.
Согласно общему подходу, игрок 1 рассматривает стратегии игроков 2, 3, … как не поддающиеся его контролю и выбирает свою стратегию так, чтобы максимально увеличить собственный выигрыш. Следовательно, для каждого заданного множества значений y, z, … выбор игроком 1 значения х максимизирует X = F (x, y, z, …). При использовании дифференциального исчисления условие такой максимизации состоит в том, что производная от X по х при постоянном значении y, z, … (это частная производная) равна нулю. Для особых функций существуют простые формулы, подобные приведенной выше и использованной для квадратичной функции. И даже если алгебраические формулировки или исчисление слишком сложны, есть немало компьютерных программ, которые составят для вас таблицы или построят графики наилучших ответов. Какой бы метод вы ни применили, вы можете найти уравнение оптимального выбора игроком 1 значения x при заданных значениях y, z, …, описывающее функцию наилучшего ответа игрока 1. Аналогичным способом можно найти функции наилучших ответов всех остальных игроков.
Функции наилучших ответов соответствуют числу стратегий в игре и могут быть решены одновременно при условии, что стратегические переменные рассматриваются как неизвестные величины. Это решение и есть равновесие Нэша, которое мы ищем. В одних играх может быть множество решений, обеспечивающих множество равновесий Нэша, в других решение может отсутствовать, что требует дальнейшего анализа, например включения смешанных стратегий.
2. Критический анализ концепции равновесия Нэша
Хотя равновесие Нэша — важнейшая концепция решения игр с одновременными ходами, оно стало объектом ряда теоретических критических замечаний. В данном разделе мы кратко рассмотрим некоторые из них, а также приведем контраргументы, подкрепляя каждый примером. Отдельные критические замечания противоречат друг другу; есть и подлежащие опровержению при более тщательном анализе игр. Некоторые утверждают, что сама концепция равновесия Нэша неполная, и предлагают дополненные или расширенные концепции с более эффективными свойствами. Мы сформулируем в данном разделе одну из таких альтернатив и укажем еще на несколько в последующих главах. Мы убеждены, что наши объяснения помогут вам заново обрести, хотя и с оговорками, уверенность в целесообразности применения концепции равновесия Нэша. Однако определенные серьезные сомнения остаются неразрешенными, и это говорит о том, что теорию игр пока еще нельзя назвать окончательно сформировавшейся наукой. Но даже этот факт должен воодушевить начинающих специалистов по теории игр, поскольку открывает перед ними широкое поле для новых идей и исследований. Неразвивающаяся наука — мертвая наука.
Давайте начнем с анализа основного фактора привлекательности концепции равновесия Нэша. Большинство игр в этой книге относятся к категории некооперативных, то есть тех, в которых игроки действуют независимо друг от друга. Следовательно, было бы естественно предположить, что если действие игрока нельзя назвать лучшим согласно его системе ценностей (шкале выигрышей) в контексте действий других игроков, то он изменит его. Иными словами, весьма заманчиво предположить, что действие каждого игрока будет представлять собой наилучший ответ на действия остальных игроков. Равновесие Нэша обладает именно таким свойством «одновременных наилучших ответов»; собственно говоря, это и есть его определение. При любом предполагаемом исходе, не являющемся равновесием Нэша, минимум один игрок мог бы добиться более выгодных для себя результатов, переключившись на другое действие.
Такие соображения заставили нобелевского лауреата Роджера Майерсона возразить против критических замечаний в адрес равновесия Нэша, основанных на интуитивной привлекательности использования другой стратегии. В качестве контрдовода Майерсон просто переложил бремя доказывания на критика. «Когда меня спрашивают, почему участники игры должны вести себя так, как предписывает равновесие Нэша, — сказал он, — мой любимый ответ — спросить “Почему бы нет?” и предоставить сомневающемуся возможность предложить свой вариант того, что, по его мнению, должны делать игроки. Если этот вариант не является равновесием Нэша, тогда… мы можем продемонстрировать, что он бы свел к нулю собственную обоснованность, если бы игроки считали его точным описанием поведения друг друга».
А. Решение проблемы риска в равновесии Нэша
Некоторые критики утверждают, что концепция равновесия Нэша не уделяет должного внимания риску. В ряде игр можно найти стратегии, отличающиеся от стратегий равновесия Нэша тем, что они более безопасны, а значит, было бы целесообразнее выбрать именно их. Мы предлагаем два примера игр такого типа. Автор первого — профессор экономики Калифорнийского университета в Беркли Джон Морган; таблица этой игры представлена на рис. 5.3.
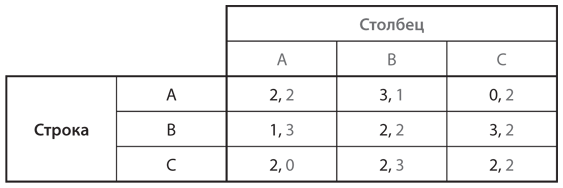
Рис. 5.3. Игра со спорным равновесием Нэша
Анализ наилучших ответов позволяет быстро определить, что в этой игре есть единственное равновесие Нэша, а именно сочетание стратегий А, А, обеспечивающее выигрыши 2, 2. Но вы, как и многие другие участники экспериментов, проведенных Морганом, можете подумать, что стратегия С весьма привлекательна по двум причинам. Во-первых, она гарантирует тот же выигрыш, что и при равновесии Нэша, то есть 2, тогда как, выбрав стратегию из равновесия Нэша А, вы получите выигрыш 2, только если другой игрок тоже выберет А. Зачем же идти на такой риск? Более того, если вы считаете, что другой игрок также может прибегнуть к подобному логическому обоснованию целесообразности выбора стратегии С, то вы совершили бы серьезную ошибку, предпочтя стратегию А, поскольку в таком случае вы получите выигрыш 0, тогда как могли бы получить 2, применив стратегию С.
Майерсон ответил на это так: «Не спешите. Если вы действительно считаете, что другой игрок рассуждает подобным образом и выберет стратегию С, то вам следует применить стратегию В, чтобы получить выигрыш 3. А если вы думаете, что другой игрок тоже так думает и выберет стратегию В, тогда вашим наилучшим ответом на стратегию В была бы стратегия А. А если вы полагаете, что другой игрок также это поймет, вы должны выбрать свой наилучший ответ на А, то есть стратегию А. Вот мы и вернулись к равновесию Нэша!» Как видите, критика в адрес равновесия Нэша и аргументы против нее — уже сами по себе нечто вроде интеллектуальной игры, причем довольно интересной.
Второй, еще более впечатляющий пример сформулировал экономист Стэнфордской бизнес-школы Дэвид Крепс. Таблица игры приведена на рис. 5.4. Прежде чем приступить к ее теоретическому анализу, вы должны представить, что действительно играете в нее в качестве игрока А. Какое из двух действий вы выбрали бы?
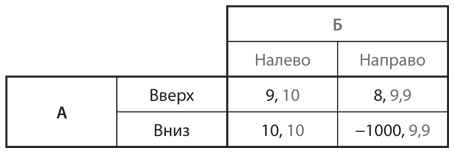
Рис. 5.4. Катастрофическое равновесие Нэша?
Запомните свой ответ на заданный выше вопрос, и продолжим анализ игры. Начав с поиска доминирующих стратегий, мы увидим, что у игрока А их нет, а у игрока Б есть. Выбор стратегии «налево» гарантирует игроку Б выигрыш 10, что бы ни сделал игрок А, тогда как в случае выбора стратегии «направо» (также при любых действиях игрока А) он получит выигрыш 9,9. Следовательно, игрок Б должен играть «налево». При условии, что игрок Б предпочтет «налево», игроку А лучше выбрать «вниз». Единственное равновесие Нэша в чистых стратегиях в этой игре — «вниз»/«налево», при таком ее исходе каждый участник получит выигрыш 10.
Проблема здесь в том, что многие (хотя и не все) люди, играющие роль игрока А, не выбирают стратегию «вниз». (А что выбрали вы?) Так поступают как те, кто много лет изучает теорию игр, так и те, кто никогда не слышал об этом предмете. Если у игрока А есть какие-либо сомнения по поводу выигрыша игрока Б или его рациональности, то для него гораздо безопаснее выбрать стратегию «вверх», чем равновесную стратегию «вниз». Но что если бы игрок А считал, что выигрыши совпадают с тем, что показано на , а в действительности выигрыши игрока Б были бы совсем другими: выигрыш 9,9 соответствовал бы стратегии «налево», а выигрыш 10 — стратегии «направо»? Что если бы значение 9,9 было приближенным, а на самом деле точный выигрыш составлял бы 10,1? Что если бы у Б была совсем иная система ценностей или на самом деле он не относится к числу рациональных игроков и мог бы выбрать «неправильное» действие просто ради забавы? Очевидно, что наши исходные предположения о совершенной информации и рациональности действительно могут играть важную роль в процессе анализа, используемого нами при изучении стратегии. Колебания относительно игроков могут изменить те равновесия, наличие которых мы предсказали бы при обычных условиях, а также поставить под сомнение корректность концепции равновесия Нэша.
Однако реальная проблема со многими такого рода примерами не в том, что концепция равновесия Нэша неприемлема, а в том, что эти примеры иллюстрируют ее неподобающе упрощенным способом. Если в приведенном выше примере есть какие-то сомнения в выигрышах игрока Б, то этот факт должен стать неотъемлемой частью анализа. Если игрок А не знает выигрышей игрока Б, значит, это игра с асимметричной информацией (мы ее сможем обсудить только в ). Но в данном примере представлена сравнительно простая игра такого типа, и мы можем без особого труда проанализировать ее равновесие.
Предположим, игрок А полагает, что существует вероятность p того, что выигрыши игрока Б при выборе стратегий «налево» и «направо» противоположны выигрышам, представленным на ; следовательно, (1 – p) — это вероятность того, что выигрыши игрока Б соответствуют информации на рисунке. Поскольку игрок А вынужден действовать, не зная фактических выигрышей игрока Б, он должен применить свою стратегию как «наилучшую в среднем». В данном примере расчеты достаточно просты, так как в каждом случае у игрока Б есть доминирующая стратегия; единственная проблема для игрока А — то, что в двух разных случаях у игрока Б разные доминирующие стратегии. С вероятностью (1 – p) доминирующая стратегия игрока Б — «налево» (случай, показанный на рисунке), а с вероятностью p его доминирующая стратегия — «направо» (противоположный случай). Таким образом, если игрок А выберет «вверх», то с вероятностью (1 – p) он будет играть против Б, применившего «налево», а значит, получит выигрыш 9; с вероятностью p игроку А предстоит вступить в игру с игроком Б, выбравшим «справа», и, стало быть, он получит выигрыш 8. Итак, статистическое, или взвешенное по вероятности среднее значение выигрыша игрока А при выборе стратегии «вверх» составляет 9(1 – p) + 8p. Аналогично статистическое, или взвешенное по вероятности, среднее значение выигрыша игрока А при использовании стратегии «вниз» равно 10(1 – p) – 1000p. Следовательно, для игрока А предпочтительнее стратегия «вверх», если
9(1 – p) + 8p > 10(1 – p) – 1000p, или p > 1 / 1009.
Таким образом, при наличии даже малейшей вероятности того, что выигрыши игрока Б противоположны выигрышам на , игроку А лучше выбрать стратегию «вверх». В данном случае правильно выполненный анализ, основанный на рациональном поведении, не противоречит ни интуитивным догадкам, ни экспериментальным данным.
При выполнении этих вычислений мы исходили из предположения, что, столкнувшись с неопределенностью в отношении выигрышей, игрок А рассчитает их статистическое среднее значение в случае различных действий и выберет действие, обеспечивающее самое высокое среднестатистическое значение выигрыша. Это неявное допущение хотя и соответствует цели данного примера, но сопряжено с определенными проблемами. Например, оно подразумевает, что человек, столкнувшийся с двумя ситуациями, в одной из которых он выиграет или проиграет 10 долларов с вероятностью 50 на 50, а в другой выиграет 10 001 доллар и проиграет 10 000 долларов с той же вероятностью, должен выбрать вторую ситуацию, поскольку она обеспечивает среднестатистический выигрыш в размере 50 центов (1/2 × 10 001 – 1/2 × 10 000), тогда как первая принесет нулевой выигрыш (1/2 × 10 – 1/2 × 10). Однако многие сочли бы, что вторая ситуация гораздо рискованнее, а потому предпочли бы первую. Решить эту проблему достаточно легко. В показано, как создание нелинейной шкалы выигрышей, соответствующих денежным суммам, позволяет человеку, принимающему решение, предусмотреть как риск, так и прибыль. А в продемонстрировано, как можно использовать эту концепцию для того, чтобы понять, как люди реагируют на риск в своей жизни — например, разделяют его с другими или покупают страховку.
Б. Множественность равновесий Нэша
Еще одно критическое замечание в адрес концепции равновесия Нэша строится на наблюдении, что во многих играх присутствует множество равновесий Нэша, а значит, данная концепция неспособна определить исходы игры достаточно точно для того, чтобы давать однозначные прогнозы. Данный аргумент не требует от нас отказа от концепции равновесия Нэша, а скорее подразумевает, что при необходимости получить однозначный прогноз на основании нашей гипотезы мы должны включить некий критерий, который поможет нам решить, какое именно из множества равновесий Нэша выбрать.
В мы изучили много координационных игр со множеством равновесий. Из всех этих равновесий игроки могут выбрать одно в качестве фокальной точки при наличии у них общих социальных, культурных или исторических знаний. Рассмотрим координационную игру, в которую сыграли студенты Стэнфордского университета. За одним игроком закрепили Бостон, за другим — Сан-Франциско. Затем каждому студенту вручили список из девяти американских городов (Атланта, Чикаго, Даллас, Денвер, Хьюстон, Лос-Анджелес, Нью-Йорк, Филадельфия и Сиэтл) и попросили выбрать подмножество городов. Оба делали выбор одновременно и независимо друг от друга и могли получить приз только при условии, что их выбор приведет к формированию двух непересекающихся подмножеств городов. Несмотря на наличие 512 других равновесий Нэша, если оба студента были американцами или гражданами США, довольно долго прожившими в стране, более чем в 80 процентах случаев они выбирали единственное равновесие по географическому принципу. Студент, за которым был закреплен Бостон, указывал все города к востоку от Миссисипи, а студент, которому соответствовал Сан-Франциско, — все города к западу от Миссисипи. Вероятность такой координации существенно снижалась, когда один или оба студента не были гражданами США. Тогда выбор порой делался в алфавитном порядке, но с гораздо меньшим уровнем координации по той же точке раздела.
Характеристики самой игры в сочетании с общим культурным опытом могут способствовать сходимости ожиданий. В качестве еще одного примера множественности равновесий рассмотрим игру, в которой два игрока одновременно и независимо друг от друга записывают, какую долю от 100 долларов каждый из них хотел бы получить. Если сумма указанных ими чисел не превышает 100 долларов, каждый игрок получает то, что записал, если превышает, оба ничего не получают. Равновесие Нэша наблюдается в случае, если при любом значении x один игрок напишет x, а другой — (100 – x). Следовательно, в этой игре есть практически бесконечный диапазон равновесий Нэша. Однако на практике фокальной точкой чаще всего становится вариант 50 на 50. Данная социальная норма равенства или справедливости, кажется, насколько глубоко укоренилась, что стала почти инстинктивной: игроки, выбирающие 50 долларов, утверждают, что это очевидный ответ. Для того чтобы это действительно была фокальная точка, это не только должно быть очевидно для всех, но каждый должен знать, что это очевидно для всех, и все должны знать, что… Иными словами, такая очевидность должна быть общим знанием. Но так бывает далеко не всегда, что подтверждает ситуация, в которой один игрок — женщина из просвещенного, эгалитарного общества, считающая очевидным разделение 50 на 50, а другой — мужчина из патриархального общества, убежденный, что о каком бы дележе ни шла речь, мужчина должен получить в три раза больше женщины. В этом случае оба сделают то, что очевидно для нее и для него, и останутся ни с чем, поскольку очевидное решение для каждого из них не будет очевидным в качестве общего знания для обоих.
Фокальная точка часто возникает в результате случайного стечения обстоятельств, а создание фокальных точек там, где их на самом деле нет, — своего рода искусство, требующее пристального внимания к историческому и культурному контексту игры, а не просто ее математического описания. Это беспокоит многих специалистов по теории игр, которые предпочли бы, чтобы исход игры зависел исключительно от ее абстрактного описания: игроки и их стратегии должны быть определены числами безо всяких внешних ассоциаций. Мы с этим не согласны. На наш взгляд, исторический и культурный контекст так же важен для игры, как и ее сугубо математическое описание, и если он помогает выбрать уникальный исход игры из множества равновесий Нэша, то это, безусловно, плюс.
В мы покажем, что игры с последовательными ходами могут иметь множество равновесий Нэша. Там же введем условие о достоверности, позволяющее выбрать конкретное равновесие; как оказалось, в его качестве выступает, по сути, равновесие обратных рассуждений, о котором рассказывалось в . В более сложных играх с асимметричностью информации или иными трудностями вводятся другие ограничения под названием уточнения, позволяющие идентифицировать и исключить из рассмотрения в некотором роде бессмысленные равновесия Нэша. В мы рассмотрим один процесс подобного уточнения, выбирающий исход под названием совершенное байесовское равновесие. Обоснование такого уточнения зачастую имеет свою специфику в играх определенного типа; оно оговаривает, как игроки должны обновлять свою информацию, наблюдая за действиями других игроков. Каждая такая оговорка чаще всего абсолютно уместна в своем контексте, поэтому во многих играх не так уж трудно исключить большинство равновесий Нэша, а значит, и снизить неоднозначность прогнозирования.
Тогда как в одних играх может быть слишком много равновесий Нэша, в других они могут отсутствовать вообще. Мы приводили пример подобной игры в , а также уточнили, что равновесие Нэша можно восстановить, расширив концепцию стратегии на случайные комбинации стратегий. В мы объясним и проанализируем равновесия Нэша в смешанных стратегиях. На более высоких уровнях теории игр существуют и более сложные примеры игр, в которых равновесия Нэша нет и в смешанных стратегиях. Однако такая дополнительная сложность не имеет отношения к рассматриваемым в данной книге типам анализа и областям применения, поэтому мы не будем затрагивать здесь эту тему.
В. Требования рациональности в равновесии Нэша
Как вы уже знаете, равновесие Нэша можно рассматривать как систему стратегических вариантов выбора каждого игрока, а также его убеждений в отношении выбора других игроков. В случае равновесия 1) выбор каждого игрока должен обеспечивать ему лучший выигрыш с учетом его убеждения в отношении выбора других игроков; 2) убеждение каждого игрока должно быть правильным, то есть его фактический выбор должен быть именно таким, каким он должен быть, по его твердому убеждению. Такова естественная интерпретация требований о взаимной согласованности рационального выбора отдельных игроков. Если у всех игроков есть общее знание того, что они рациональны, то как может один из них иметь рациональные убеждения в отношении выбора других игроков, не соответствующие рациональной реакции на его собственные действия?
Для того чтобы изучить этот вопрос, рассмотрим игру три на три, представленную на рис. 5.5. Анализ наилучших ответов позволяет быстро определить, что в ней всего одно равновесие Нэша, а именно R2, C2, обеспечивающее выигрыш 3, 3. В этом равновесии Строка выбирает вариант R2, исходя из убеждения, что Столбец сыграет C2. Почему Строка в этом убеждена? Потому что она знает Столбца как рационального игрока, но в то же время она должна считать, что Столбец убежден в ее выборе варианта R2 по той причине, что вариант С2 не будет его наилучшим выбором, если бы он полагал, что Строка сыграет либо R1, либо R3. Таким образом, суть этого утверждения состоит в том, что убеждения, полученные в результате рационального процесса формирования, должны быть правильными.
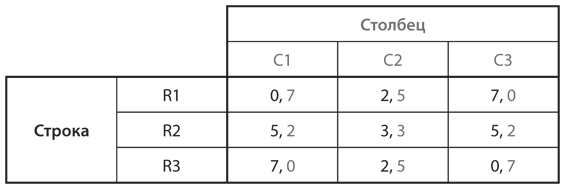
Рис. 5.5. Обоснование выбора посредством цепочки убеждений и ответных действий
Проблема такой аргументации состоит в том, что она ограничена одним циклом рассуждений об убеждениях. Продолжив их, мы можем обосновать и другие комбинации вариантов выбора. Например, можно рационально обосновать выбор Строкой варианта R1. Для этого отметим, что R1 — лучший выбор Строки в случае, если она убеждена, что Столбец сыграет С3. Почему Строка в этом убеждена? Потому что уверена, что Столбец убежден в том, что она выберет R3. Строка обосновывает это убеждение, считая, что Столбец убежден в том, что Строка убеждена в том, что Столбец сыграет С1, будучи убежденным в том, что Строка предпочтет вариант R1, будучи, в свою очередь, убежденной в том, что… Каждое звено этой цепочки убеждений абсолютно рационально.
Таким образом, рациональность сама по себе не объясняет равновесия Нэша. Существуют более сложные доводы такого рода, действительно позволяющие обосновать особый вид равновесия Нэша, при котором игроки могут поставить свои стратегии в зависимость от поддающегося наблюдению инструмента рандомизации (случайного выбора). Однако мы оставим эту тему для более углубленного изучения и сформулируем в следующем разделе более простую концепцию, отражающую то, что логически вытекает из общего знания игроков только об их рациональности.
3. Рационализация
Какие стратегические варианты выбора в играх можно обосновать, исходя исключительно из рациональности? В матрице игры на мы можем объяснить любую пару стратегий, по одной на каждого игрока, посредством применения той же логики, что и в . Иными словами, можем обосновать любую из девяти возможных комбинаций. Следовательно, рациональность в чистом виде не позволяет нам сократить совокупность вероятных исходов игры или вообще спрогнозировать их. Присуще ли это всем играм? Нет. Например, если стратегия доминируемая, ее можно исключить из рассмотрения на основе одной только рациональности. А когда игроки осознают, что их соперники, будучи рациональными, не выберут доминируемые стратегии, исходя из такого общего знания можно выполнить итеративное исключение доминируемых стратегий. Лучшее ли это из доступных действий? Нет. Можно продолжить дальнейшее исключение стратегий, воспользовавшись несколько более сильным свойством, чем доминируемость в чистых стратегиях. Оно определяет стратегии, которые не могут быть наилучшим ответом. Стратегии, оставшиеся после такой процедуры исключения, называются рационализируемыми, а сама концепция — рационализацией.
Зачем вводить эту дополнительную концепцию, и что она нам дает? Что касается первого вопроса, полезно знать, насколько можно сузить совокупность возможных исходов игры на основании одной лишь рациональности игроков, не прибегая к правильности ожиданий относительно фактического выбора игрока. Иногда можно определить, что игрок не выберет то или иное действие или действия, даже если нельзя вычислить, какое именно действие он все же выберет. Ответ на второй вопрос зависит от контекста. Порой рационализация вообще не позволяет сократить совокупность исходов игры. Именно так было в примере три на три, представленном на . Подчас рационализация позволяет это сделать только до определенной степени, но не до равновесия Нэша, если оно в игре всего одно, или не до совокупности равновесий Нэша, если их в игре несколько. Примером такой ситуации может служить расширенный до матрицы четыре на четыре предыдущий пример, который рассматривается в ниже. Иногда сокращение совокупности возможных исходов игры приводит к определению единственного равновесия Нэша, причем в подобных случаях мы имеем его более веское обоснование, опирающееся исключительно на рациональность, без предположений о правильности ожиданий. Ниже в представлен пример игры с конкуренцией по количеству, в котором аргументация на основе концепции рационализации позволяет найти в ней единственное равновесие Нэша.
А. Применение концепции рационализации
Рассмотрим игру на рис. 5.6, аналогичную той, что приведена на , но с дополнительной стратегией на каждого игрока. Как отмечалось выше, девять комбинаций стратегий, в которые входит одна из первых трех стратегий для каждого из игроков, можно обосновать посредством цепочки убеждений игроков в отношении убеждений друг друга. Это верно и в увеличенной матрице. Но подходит ли такой способ для стратегий R4 и C4?
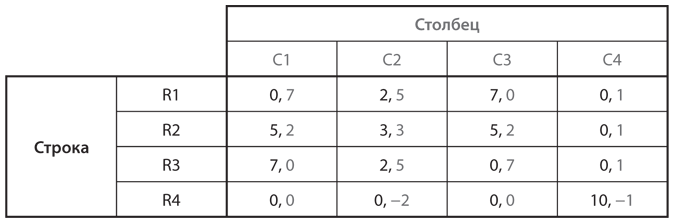
Рис. 5.6. Рационализируемые стратегии
Может ли Строка исходить из убеждения, что Столбец выберет стратегию C4? В его основе должны лежать убеждения Столбца в отношении выбора Строки. Могут ли они сделать стратегию С4 наилучшим ответом Столбца? Нет. Если Столбец полагает, что Строка сыграет R2, его наилучший ответ С2. Если Столбец считает, что Строка предпочтет R3, то его наилучший ответ С3. А если Столбец убежден, что Строка выберет R4, тогда его наилучший ответ либо С1, либо С3. Следовательно, С4 не может быть наилучшим ответом Столбца. Это означает, что Строка, зная о рациональности Столбца, ни в коем случае не припишет ему выбор стратегии С4. Стало быть, Строка не должна исходить из убеждения, что Столбец сыграет С4.
Обратите внимание, что хотя стратегия С4 не может быть наилучшим ответом, она не является доминируемой по отношению к стратегиям С1, С2 и С3. Для Столбца она предпочтительнее стратегии С1 против стратегии Строки R3, предпочтительнее стратегии С2 против стратегии Строки R4 и предпочтительнее стратегии С3 против стратегии Строки R1. Если стратегия все же доминируемая, она тоже не может быть наилучшим ответом. Таким образом, «стратегия, которая не может быть наилучшим ответом», — более общая концепция, чем «доминируемая стратегия». Исключение таких стратегий возможно даже тогда, когда исключение доминируемых стратегий невозможно. Следовательно, исключение стратегий, которые не могут быть наилучшим ответом, способно сузить совокупность вероятных исходов игры в большей степени, чем исключение доминируемых стратегий.
Исключение стратегий, которые не могут быть наилучшим ответом, также можно выполнять в итеративном режиме. Поскольку рациональный игрок Строка не может исходить из убеждения, что рациональный игрок Столбец выберет стратегию С4, рациональный игрок Столбец должен это предвидеть. Учитывая, что R4 — наилучший ответ Строки только на стратегию С4, Столбец не должен думать, что Строка сыграет R4. Следовательно, R4 и С4 не могут входить в набор рационализируемых стратегий. Концепция рационализации действительно позволяет сократить совокупность возможных исходов данной игры.
Если в игре есть равновесие Нэша, оно будет рационализируемым и его можно подтвердить посредством простой системы убеждений, состоящей из одного цикла, как в представленном выше . Но в более общем плане, даже если в игре нет равновесия Нэша, она может иметь рационализируемые исходы. Возьмем в качестве примера игру два на два, полученную из игры на или , в которой оставлены только стратегии R1 и R3 для Строки и С1 и С3 для Столбца. Легко увидеть, что в этой игре нет равновесия Нэша в чистых стратегиях. Однако все четыре ее исхода рационализируемы посредством такой же цепочки убеждений, как выстроенная выше и охватывающая эти стратегии.
Таким образом, концепция рационализации представляет собой возможный способ решения игр с отсутствием равновесия Нэша. Что еще более важно, эта концепция подсказывает нам, как сократить совокупность вероятных исходов игры исключительно на основании рациональности.
Б. Рационализация может привести к равновесию Нэша
В некоторых играх итеративное исключение стратегий, которые не могут быть наилучшим ответом, может сократить всю совокупность возможных исходов до равновесия Нэша. Обратите внимание, что мы сказали «может», а не «должно». Но если подобное все же происходит, это очень полезно, поскольку позволяет подкрепить доводы в пользу равновесия Нэша путем утверждения, что оно следует исключительно из рациональных мнений игроков о рассуждениях друг друга. Интересно, что один класс игр, решаемых таким способом, играет важную роль в экономике. К нему относится конкуренция между компаниями при определении количества производимой продукции, когда они знают, что от ее общего объема на рынке зависит цена.
Мы проиллюстрируем игру такого типа в контексте небольшого прибрежного городка. В нем две некие рыбацкие лодки каждый вечер уходят в море, а утром возвращаются с уловом и выставляют его на рынок. Игра разыгрывается во времена, когда еще не было современного холодильного оборудования, поэтому вся рыба должна быть продана и съедена в тот же день. В океане неподалеку от города полно рыбы, поэтому владелец каждой лодки может решать, сколько рыбы поймать за ночь. Но каждый из них также знает, что избыток рыбы на рынке приведет к снижению цен и прибыли.
Предположим, что если одна лодка выставит на рынок R бочек рыбы, а другая S бочек, то цена P (в дукатах за бочку) будет равна P = 60 – (R + S). Допустим также, что две лодки и их команды несколько отличаются по эффективности рыбной ловли: затраты первой лодки на ловлю рыбы составляют 30 дукатов на одну бочку, тогда как второй — 36 дукатов на бочку.
Теперь мы можем записать формулы определения прибыли двух владельцев лодок U и V с учетом их стратегий R и S.
U = [(60 – R – S) – 30]R = (30 – S)R – R2,
V = [(60 – R – S) – 36]S = (24 – R)S – S2.
На основании этих формул выигрышей можно построить кривые наилучших ответов и найти равновесие Нэша. Как и в примере игры с ценовой конкуренцией из , выигрыш каждого игрока представляет собой квадратичную функцию его собственной стратегии при условии неизменности стратегии другого игрока. Следовательно, в данном случае можно применить математические методы, изложенные в данной главы и в .
Наилучший ответ первой лодки R должен максимизировать значение U для каждого заданного значения S другой лодки. При использовании дифференциального исчисления это означает, что мы должны продифференцировать U по R при фиксированном значении S и приравнять производную к нулю, что дает следующее уравнение:
(30 – S) – 2R = 0; R = 15 – S / 2.
Подход без дифференциального исчисления использует результат, согласно которому значение R, максимизирующее значение U, равно R = B / (2C), где B = 30 – S, а C = 1. Это дает R = (30 – S) / 2, или R = 15 – S / 2.
Аналогичным образом уравнение наилучшего ответа второй лодки можно найти, выбрав значение S, максимизирующее значение V при каждом фиксированном значении R, что дает следующее значение:
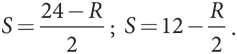
Равновесие Нэша можно найти посредством совместного решения двух уравнений наилучших ответов для R и S, что не так уж трудно сделать, поэтому мы просто приведем результаты. Количество: R = 12, S = 6; цена: P = 42; прибыль: U = 144, V = 36.
На рис. 5.7 представлены графики наилучших ответов двух рыбаков (обозначенные как BR1 и BR2 с указанием соответствующих уравнений), а также равновесие Нэша (обозначенное как N с указанием координат) на пересечении двух линий. Кроме того, на рис. 5.7 также показано, как сократить совокупность убеждений игроков в отношении выбора друг друга посредством итеративного исключения стратегий, которые не могут быть наилучшим ответом.
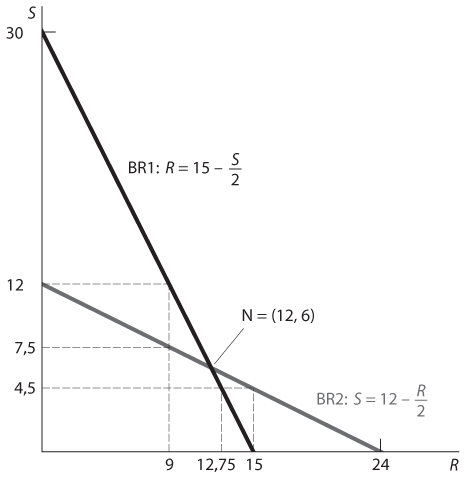
Рис. 5.7. Поиск равновесия Нэша с помощью рационализации
Какие значения S, по рациональному убеждению владельца первой лодки, выберет владелец второй лодки? Это зависит от того, какой улов, по мнению владельца второй лодки, получит владелец первой лодки. Но каким бы ни был этот улов, наилучшие ответы владельца второй лодки находятся в диапазоне от 0 до 12 бочек. Следовательно, владелец первой лодки не может рационально считать, что владелец второй лодки выберет что-то другое: все отрицательные варианты выбора (что очевидно) и все значения S, превышающие 12 бочек (что менее очевидно), исключаются. Точно так же владелец второй лодки не может рационально считать, что владелец первой лодки выловит рыбы меньше 0 или больше 15 бочек.
Теперь перейдем ко второму циклу рассуждений. Когда владелец первой лодки ограничит варианты выбора значений S владельцем второй лодки диапазоном от 0 до 12 бочек, его собственные варианты выбора значений R будут ограничены диапазоном наилучших ответов на диапазон значений S. Наилучший ответ на S = 0 — это R = 15, а наилучший ответ на S = 12 — это R = 15 – 12 / 2 = 9. Поскольку график BR1 наклонен вниз, все значения R, допустимые на данном этапе рассуждений, лежат в диапазоне от 9 до 15. Точно так же выбор владельцем второй лодки значений S ограничен диапазоном наилучших ответов на R от 0 до 15, точнее говоря, значениями от S = 12 до S = 12 – 15 / 2 = 4,5. Эти ограниченные диапазоны значений показаны на на осях координат.
Третий цикл рассуждений сужает диапазоны значений еще больше. Поскольку значение R должно составлять минимум 9, а график BR2 имеет отрицательный наклон, S может быть не более чем наилучшим ответом на 9; в частности, S = 12 – 9 / 2 = 7,5. В ходе второго цикла рассуждений уже было показано, что значение S должно быть как минимум 4,5. Следовательно, теперь значения S ограничены диапазоном от 4,5 до 7,5. Кроме того, так как значение S должно быть не менее 4,5, значение R может составлять не более 15 – 4,5 / 2 = 12,75. Во втором цикле рассуждений мы узнали, что значение R должно равняться минимум 9, а значит, теперь оно ограничено диапазоном от 9 до 12,75.
Эту последовательность циклов рассуждений можно продолжать сколько угодно, но уже сейчас очевидно, что последовательное сужение диапазонов значений двух показателей сводит эти значения к равновесию Нэша, R = 12 и S = 6. Таким образом, равновесие Нэша — единственный исход игры, остающийся после итеративного исключения стратегий, которые не могут быть наилучшим ответом. Мы знаем, что в общем аргументация на основе концепции рационализации не обязательно должна сводить исходы игры к равновесиям Нэша, а значит, это особое свойство данного примера. В действительности этот процесс применим к целому классу игр и позволяет решить любую игру, имеющую единственное равновесие Нэша на пересечении нисходящих кривых наилучших ответов.
Эту аргументацию следует отличать от прежней, основанной на последовательности наилучших ответов. Тогда ход рассуждений выглядел следующим образом. Начнем с любой стратегии одного из игроков, скажем R = 18. В этом случае наилучший ответ другого игрока S = 12 – 18/2 = 3. Наилучший ответ R на S = 3 — это R = 15 – 3/2 = 13,5. В свою очередь, наилучший ответ S на R =13,5 — 12 – 13,5/2 = 5,25. Тогда наилучший ответ R против этого значения S составляет R = 15 – 5,25/2 = 12,375. И так далее.
Цепочка рассуждений в прежней аргументации также сходится к равновесию Нэша, но в ней есть один недостаток. Речь идет об игре с одновременными ходами, разыгрываемой только раз. В такой ситуации невозможно, чтобы один игрок отреагировал на выбор другого игрока, после чего первый игрок снова предпринял ответное действие и т. д. Если бы такая динамика игры допускалась, разве игроки не предвидели бы реакцию друг друга и не предприняли бы совсем другие действия?
Аргументация на основе концепции рационализации представляет собой нечто иное. В ней четко учитывается тот факт, что игра проходит только раз и сводится к одновременному выполнению ходов. Все размышления относительно цепочки наилучших ответов выполняются с опережением событий, а все последующие циклы рассуждений и ответных действий носят сугубо концептуальный характер. Игроки реагируют не на фактический выбор, а лишь на расчетные значения того выбора, который так и не будет сделан. Весь процесс протекает исключительно в головах игроков.
4. Эмпирические данные о равновесии Нэша
В , посвященной анализу эмпирических данных об играх с последовательными ходами и методу обратных рассуждений, мы представили данные, полученные в ходе наблюдений за играми, происходящими в реальной жизни, и играми, специально разработанными для проверки теории в лабораторных условиях. Там же мы выделили различные достоинства и недостатки двух методов оценки достоверности прогнозов, полученных посредством поиска равновесия методом обратных рассуждений. Аналогичные вопросы возникают и в связи с получением и интерпретацией эмпирических данных относительно равновесия Нэша в играх с одновременными ходами.
В реальных играх делаются крупные ставки, и в основном в них участвуют опытные игроки, обладающие знаниями и стимулами для применения эффективных стратегий. Но в таких ситуациях присутствует много факторов, выходящих за рамки того, что изучает теория. Например, в реальных играх трудно отслеживать количественные выигрыши, которые получили бы игроки при всех возможных комбинациях стратегий. Поэтому, если их поведение не подтверждает теоретические прогнозы, невозможно определить, обусловлено ли это ошибочностью теории или тем, что какие-то иные факторы превосходят стратегические соображения.
В ходе лабораторных экспериментов эти факторы пытаются учитывать, чтобы обеспечить более точную проверку теории. Но организаторы экспериментов зачастую привлекают неопытных игроков и предоставляют им слишком мало времени и относительно слабые стимулы для изучения игры. Столкнувшись с новой игрой, большинство из нас поначалу с трудом ориентируется в ней и пробует играть бессистемно. По этой причине несколько ее первых раундов в условиях эксперимента могут представлять собой этап обучения, а не равновесие, которое нашел бы в игре опытный игрок. Обычно такую неопытность и обучение учитывают, исключая из рассмотрения данные первых нескольких раундов игры, однако этап обучения может длиться дольше, чем одно утро или вторая половина дня, что зачастую составляет предельную продолжительность лабораторных сеансов.
А. Лабораторные эксперименты
За три прошедших десятилетия ученые провели множество лабораторных исследований в целях проверки поведения людей в определенных интерактивных стратегических ситуациях. В частности, исследователи пытаются найти ответ на вопрос: «Выбирают ли участники игры стратегии равновесия Нэша?» Проанализировав эту работу, Дуглас Дэвис и Чарльз Холт пришли к выводу, что в относительно простых одноходовых играх с единственным равновесием Нэша оно «обретает значительную притягательную силу… после нескольких повторений игры с разными партнерами». Однако успех этой теории носит переменный характер в более сложных ситуациях, например при наличии множества равновесий Нэша, когда эмоциональные факторы выводят выигрыши за пределы оговоренных денежных сумм, когда для поиска равновесия Нэша требуются более сложные расчеты или когда игра повторно проводится с одними и теми же партнерами. Ниже представлен краткий анализ эффективности равновесия Нэша в нескольких подобных ситуациях.
I.-Выбор из множества равновесий Нэша. В приведено несколько примеров, показывающих, что иногда фокальные точки помогают игрокам выбрать из множества равновесий Нэша одно. Игрокам не удается скоординировать свои действия в 100 процентах случаев, однако обстоятельства зачастую позволяют им добиться гораздо большей координации действий, чем при случайном выборе из всей совокупности возможных равновесных стратегий. Ниже мы представляем координационную игру с одним интересным свойством: равновесие, обеспечивающее самый высокий выигрыш всем ее участникам, при этом и самое рискованное в том смысле, о котором шла речь выше в .
Джон Ван Хайк, Реймонд Батталио и Ричард Бейл описывают игру с участием 16 игроков, в которой каждый из них одновременно выбирает уровень «усилий» от 1 до 7. Индивидуальные выигрыши зависят от «результата» всей группы, который является функцией от минимального уровня усилий, выбранного любым ее членом, за вычетом затрат на эти усилия. В игре ровно семь равновесий Нэша в чистых стратегиях: любой исход, при котором все игроки выбирают один и тот же уровень усилий, представляет собой равновесие. Максимальный выигрыш (1,30 доллара на одного игрока) будет получен в случае, если все участники игры выберут уровень усилий 7, тогда как минимальный (0,70 доллара на одного игрока) — при выборе всеми игроками уровня усилий 1. Равновесие, обеспечивающее самый высокий выигрыш, — естественный кандидат на роль фокальной точки, но при этом существует риск выбрать самый высокий уровень усилий: если хотя бы один игрок выберет уровень усилий ниже вашего, то ваши дополнительные усилия будут потрачены зря. Например, если вы предпочтете вариант 7 и минимум один игрок вариант 1, вы выиграете всего 0,10 доллара — гораздо меньше, чем в случае наихудшего равновесного выигрыша в размере 0,70 доллара. Это заставляет игроков волноваться по поводу того, выберут ли другие участники игры максимальный уровень усилий; в итоге большим группам, как правило, не удается скоординировать свои действия так, чтобы обеспечить самое выгодное равновесие. Несколько игроков неизбежно выбирают более низкий уровень усилий, и в последующих раундах игра сводится к равновесию с самым низким уровнем усилий.
II.-Эмоции и социальные нормы. В в процессе анализа игр с последовательными ходами мы привели несколько примеров более щедрого отношения игроков друг к другу, чем можно было ожидать согласно равновесию Нэша. Подобные наблюдения можно сделать и в играх с одновременными ходами, таких как дилемма заключенных. Одна из причин состоит в том, что выигрыши игроков могут отличаться от тех, из которых исходит экспериментатор: помимо денег, участники игры могут относить к числу выигрышей испытываемые в ходе игры эмоции, такие как сопереживание, гнев или чувство вины. Иными словами, в системе ценностей игроков могли проявиться некоторые социальные критерии, например доброта и справедливость, которые доказали свою значимость в более широком социальном контексте и в силу этого распространяются на их поведение и в экспериментальной игре. С этой точки зрения подобные наблюдения не вскрывают недостатков самой концепции равновесия Нэша, а предостерегают против ее использования при наивных или ошибочных исходных предположениях о том, какие выигрыши важны для людей. Например, было бы ошибкой полагать, что игроки всегда движимы в своих действиях эгоистичной погоней за деньгами.
III.-Когнитивные ошибки. Как мы убедились в случае экспериментальных данных по равновесию обратных рассуждений в , игроки не всегда предварительно продумывают всю игру, как и не всегда ожидают этого от других игроков. Поведение участников игры, известной как дилемма путешественников, иллюстрирует подобную ограниченность равновесия Нэша в играх с одновременными ходами. В этой игре оба путешественника во время отпуска покупают одинаковые сувениры, а на обратном пути авиакомпания теряет их багаж. Она сообщает, что намерена возместить им убытки, но ей неизвестна точная сумма ущерба. Авиаперевозчик знает, что правильная сумма должна находиться в пределах от 80 до 200 долларов на человека, поэтому проводит игру по следующей схеме. Каждый игрок может потребовать возмещения убытков в размере от 80 до 200 долларов. Авиакомпания возместит обоим игрокам сумму, которая окажется меньшей из двух заявленных. Кроме того, если они будут разниться, авиакомпания выплатит 5 долларов вознаграждения тому, кто потребовал меньше, и оштрафует на 5 долларов того, кто запросил больше.
При таких правилах игры, независимо от фактической стоимости утерянного багажа, каждый игрок заинтересован назвать более низкую сумму возмещения убытков, чем другой игрок. На самом деле единственное равновесие Нэша и единственный рационализируемый исход этой игры сводится к тому, чтобы оба указали минимальную сумму возмещения — 80 долларов. Однако в условиях эксперимента игроки редко называют 80 долларов, вместо этого требуя возмещения сумм, которые гораздо ближе к 200 долларам. (Как правило, в лаборатории реальные выигрыши исчисляются в центах, а не в долларах.) Интересно, что если размер «штрафвознаграждения» увеличивается в 10 раз, с 5 до 50 долларов, то поведение игроков существенно приближается к равновесию Нэша, а указанная ими сумма ущерба чаще всего составляет около 80 долларов. Таким образом, поведение участников эксперимента в значительной мере зависит от показателя, никак не влияющего на равновесие Нэша: единственное равновесие — это 80 долларов, независимо от суммы штрафа или вознаграждения.
Для объяснения результатов, полученных в лаборатории, Моника Капра и ее коллеги использовали теоретическую модель под названием равновесие квантильных откликов (или просто «квантильное равновесие»), первоначально предложенную Ричардом Маккелви и Томасом Палфри. Математическое описание этой модели выходит за рамки данной книги, но ее основная идея состоит в том, что она допускает возможность совершения ошибок игроками, причем вероятность определенной ошибки гораздо ниже в случае более дорогостоящих ошибок, чем в случае ошибок, незначительно уменьшающих выигрыш. Более того, в этой модели игроки ожидают друг от друга таких ошибок. Как оказалось, анализ квантильных откликов позволяет объяснить приведенные выше данные. Указание большей суммы возмещения убытков обойдется не так уж дорого при размере штрафа 5 долларов, поэтому игроки чаще называют сумму, близкую к 200 долларам, — особенно если знают, что соперники, по всей вероятности, поступят так же, а значит, выигрыш при этом может быть достаточно высоким. С другой стороны, если штраф или вознаграждение составляет 50 долларов вместо пяти, предъявление завышенных требований о возмещения ущерба может обернуться значительными потерями, поэтому игроки вряд ли будут ожидать друг от друга подобных действий. Это ожидание склоняет их в сторону равновесия Нэша, то есть 80 долларов. Благодаря такому успеху квантильное равновесие стало темой активных исследований в области теории игр.
IV.-Общее знание о рациональности. Как мы только что увидели, чтобы лучше объяснить результаты экспериментов, модель квантильного равновесия допускает вероятность того, что игроки могут не считать других участников игры в высшей степени рациональными игроками. Еще один способ объяснить данные экспериментов — предположить, что разные игроки строят свои рассуждения на разных уровнях. В стратегической игре на угадывание, часто используемой в аудиториях или лабораториях, каждому участнику предлагают выбрать число от 0 до 100. Как правило, игрокам выдают карточки, на которых они должны написать свое имя и выбранное число, поэтому данная игра относится к категории игр с одновременными ходами. После сбора карточек вычисляется среднее значение указанных чисел. Побеждает тот, чье число окажется ближе всего к оговоренной доле (например, двум третям) от среднего значения. Правила игры (вся описанная выше процедура) объявляются заранее.
Равновесие Нэша в этой игре сводится к выбору каждым игроком числа 0. В действительности игра разрешима по доминированию. Даже если каждый ее участник укажет 100, половина от среднего значения не может превысить 67, поэтому для каждого игрока выбор числа больше 67 доминируемый по отношению к выбору числа 67. Однако это должно быть понятно всем рационально рассуждающим игрокам, а значит, среднее значение не может превышать 67, а две трети от него — 44, поэтому любой выбор числа больше 44 будет доминируемым по отношению к выбору числа 44. Данный процесс итеративного удаления доминируемых стратегий продолжается до тех пор, пока не останется только число 0.
Тем не менее когда группа играет в такую игру впервые, побеждает не тот, кто выбрал число 0. Как правило, выигрышное число попадает в диапазон от 15 до 20. Чаще всего игроки указывают числа 33 и 22, из чего можно сделать вывод, что многие из них выполняют всего один-два цикла итеративного доминирования, не продолжая этот процесс дальше. Иначе говоря, игроки «уровня 1» считают, что все остальные участники игры будут выбирать числа случайным образом, со средним значением 50, поэтому в качестве наилучшего ответа указывают две трети от этого числа, то есть 33. Точно так же игроки «уровня 2» предполагают, что все остальные игроки рассуждают на «уровне 1», поэтому в качестве наилучшего ответа выбирают две трети от 33, или 22. Обратите внимание, что все эти варианты далеки от равновесия Нэша, числа 0. Создается впечатление, что многие игроки иногда выполняют ограниченное количество шагов итеративного исключения доминируемых стратегий по той причине, что ожидают от других игроков ограниченного количества циклов рассуждений.
V.-Обучение и движение в сторону равновесия. Что происходит при повторном разыгрывании стратегической игры на угадывание в одной и той же группе игроков? Аудиторные эксперименты показывают, что в ходе каждого очередного раунда выигрышное число может легко уменьшиться на 50 процентов, поскольку студенты ожидают, что все их одногруппники выберут число, не превышающее победившее в предыдущем раунде. Как правило, в третьем раунде выгрышные числа не больше (а то и меньше) 5.
Как следует интерпретировать этот результат? Критики бы заявили, что, если в игре не достигнуто точное равновесие Нэша, это опровергает теорию. Они бы утверждали, что в действительности, если у вас есть все основания полагать, что другие игроки не используют стратегии равновесия Нэша, ваш лучший выбор также не должен быть стратегией равновесия Нэша. Если вы можете определить, как другие игроки будут отклоняться от стратегий равновесия Нэша, то должны выбрать свой наилучший ответ на то, что они, по вашему мнению, предпочтут. Другие бы сказали, что в социальных науках теория не может претендовать на такой же уровень точности прогнозов, что и в таких науках, как физика и химия. Если наблюдаемые исходы игры близки к равновесию Нэша, это и есть подтверждение теории. В данном случае эксперимент не только обеспечивает это подтверждение, но и иллюстрирует процесс, посредством которого люди накапливают опыт и учатся применять стратегии, близкие к равновесию Нэша. Мы склонны согласиться с данной точкой зрения.
Примечательно одно наше наблюдение: люди учатся немного быстрее, следя за игрой со стороны, чем принимая в ней непосредственное участие. Это можно объяснить тем, что как наблюдатели они могут сфокусироваться на игре в целом и использовать аналитическое мышление. А поскольку мозг игроков занят решением задачи собственного выбора, они в меньшей степени способны увидеть более широкую картину.
Мы должны внести ясность в концепцию накопления опыта посредством участия в играх. В цитате Дэвиса и Холта в начале данного раздела говорится о повторении игры с разными партнерами. Иными словами, опыт игры следует накапливать посредством многократного участия в ней, но всякий раз с разными соперниками. Однако для того, чтобы такой процесс обучения обеспечивал исходы игры, максимально приближающиеся к равновесию Нэша, вся совокупность обучающихся игроков должна оставаться неизменной. Если в игре постоянно будут появляться новички, применяющие новые экспериментальные стратегии, исходная группа рискует утратить знания, накопленные в процессе игры друг против друга.
Если игра повторно проводится между двумя игроками или среди небольшой группы одних и тех же игроков, то два любых игрока с большой вероятностью могут неоднократно играть друг с другом. В такой ситуации повторяющаяся игра в целом сама по себе становится игрой. Равновесия Нэша в ней могут отличаться от тех, которые просто дублируют равновесие Нэша в одном раунде игры. Например, в повторяющихся дилеммах заключенных молчаливое сотрудничество может сформироваться как следствие ожиданий того, что любая временная выгода от обмана будет полностью сведена на нет последующей потерей доверия. Если игры повторяются таким способом, то процесс обучения должен включать в себя многократное участие в полных множествах таких повторений, каждый раз против других партнеров.
Б. Реальные игры
В играх, разыгрываемых в естественных условиях, нет стольких возможностей для прямых наблюдений, как в ходе лабораторных экспериментов, но тем не менее наблюдения за пределами лабораторий также позволяют получить ценные доказательства значимости равновесия Нэша. В свою очередь оно зачастую становится для социологов ценной отправной точкой для осмысления реального мира.
I.-Области применения равновесия Нэша. Одной из первых областей применения концепции равновесия Нэша по отношению к поведению субъектов реального мира стала сфера международных отношений. Томас Шеллинг первым использовал теорию игр для объяснения таких феноменов, как эскалация гонки вооружений (даже между странами, не имеющими намерения нападать друг на друга) и достоверность сдерживающих угроз. Впоследствии концепцию равновесия Нэша начали применять в этой сфере для решения вопросов о том, когда и как страна может подать достоверный сигнал о своих намерениях в ходе дипломатических переговоров или перед лицом возможной войны. В середине 1970-х теорию игр начали систематически использовать в сфере экономики и бизнеса, и количество областей применения продолжает расти.
Как мы уже говорили в данной главе, ценовая конкуренция — одна из важных областей применения равновесия Нэша. К числу других областей, в которых компаниям приходится делать стратегический выбор, относится качество продукции, инвестиции, научные исследования и разработки и т. д. Кроме того, теория игр помогла нам понять, как и когда компании, присутствующие в отрасли много лет, могут взять на себя достоверные обязательства по сдерживанию новых конкурентов — например, посредством ведения губительной ценовой войны против нового участника рынка. Теоретико-игровые модели, построенные на концепции равновесия Нэша и ее динамических обобщениях, достаточно эффективно обеспечивают необходимыми данными многие крупные отрасли промышленности, в частности автомобилестроение. Кроме того, такие модели позволяют лучше понять основные факторы конкуренции по сравнению с более старыми моделями, исходящими из совершенной конкуренции и оценочных кривых спроса и предложения.
Профессор бизнес-школы IESE в Барселоне Панкадж Гемават представил ряд исследований отдельных компаний или отраслей, подкрепив их статистическим анализом данных. Его теоретико-игровые модели чрезвычайно эффективно улучшают наше понимание нескольких на первый взгляд озадачивающих бизнес-решений по таким вопросам, как ценообразование, производственные мощности, инновации и т. д. Например, в 1970-х компания DuPont нарастила огромный объем производственных мощностей по выпуску диоксида титана. Их избыток превышал прогнозируемый рост мирового спроса на этот продукт на протяжении следующего десятилетия. Поначалу этот выбор казался ужасной стратегией, поскольку избыток мощностей мог повлечь за собой снижение рыночных цен на данный товар. Однако в DuPont с успехом предвидели, что наличие в резерве дополнительных производственных мощностей позволит компании наказывать конкурентов, занижающих цены, увеличивая объем производства и снижая цены еще больше. Это сделало DuPont ценовым лидером в своей отрасли и позволило обеспечить высокую рентабельность. Стратегия оказалась весьма эффективной, и даже 40 лет спустя компания DuPont сохраняет мировое лидерство по производству диоксида титана.
В последнее время теория игр стала самым предпочтительным инструментом изучения политических систем и институтов. Как мы увидим в , она показала, как в погоне за чьими-то целями могут осуществляться стратегические манипуляции в ходе голосования и определения повестки дня в комитетах и на выборах. В четвертой части книги представлены примеры практического применения равновесия Нэша при проведении аукционов, голосований и переговоров. Кроме того, в мы приводим свой учебный пример, посвященный Карибскому ракетному кризису.
Некоторые критики не признают ценности концепции равновесия Нэша, заявляя, что аналогичное объяснение тех же явлений можно получить с помощью уже известных общих экономических принципов, политологии и т. д. Отчасти они правы. Ряд подобных аналитических инструментов существовал еще до появления данной концепции. Например, равновесие во взаимодействии между двумя компаниями, устанавливающими цены, о котором шла речь в данной главы, известно в экономике уже более 100 лет. Равновесие Нэша можно считать общей формулировкой концепции равновесия, применимой ко всем играм. Некоторые теории стратегического голосования сформулированы еще в XVIII столетии, а представления о достоверности можно найти в «Истории Пелопонесской войны» Фукидида. Однако равновесие Нэша позволяет унифицировать все эти области применения, а значит, способствует формированию новых областей.
Кроме того, развитие теории игр обусловило появление огромного количества новых идей и областей применения, не существовавших ранее, например: как возможность нанести второй удар уменьшает страх перед внезапным нападением; как разные правила проведения аукционов влияют на характер предложения цены и доход продавца; как правительства могут успешно манипулировать фискальной и монетарной политикой с тем, чтобы добиться переизбрания даже тогда, когда опытные избиратели знают об этих попытках, и т. д. Если бы все эти задачи можно было решить с помощью ранее известных подходов, это бы уже давно было сделано.
II.-Реальные примеры обучения. Напоследок предлагаем вашему вниманию интересный пример равновесия и процесса обучения в реальной игре Главная лига бейсбола. В ней очень высокие ставки, а игроки участвуют более чем в 100 матчах в год, что создает сильную мотивацию и благоприятные возможности для обучения. Стивен Гулд обнаружил следующий замечательный пример. На протяжении большей части XX столетия максимальное значение средних коэффициентов результативности отбивания, зафиксированных на протяжении бейсбольного сезона, неизменно снижалось. Скажем, в прошлом игроки обеспечивали средний коэффициент результативности отбивания 0,400 гораздо чаще, чем сейчас. Почитатели истории бейсбола часто объясняют такое снижение, с ностальгией восклицая: «В те времена были выдающиеся игроки!» Если на секунду задуматься, сразу же возникает вопрос: почему тогда не было выдающихся питчеров, способных удерживать средний коэффициент результативности отбивания на низком уровне? Однако Гулд опровергает подобные доводы посредством более системного подхода, указывая на то, что следует анализировать все значения среднего коэффициента результативности отбивания, а не только самые высокие. В настоящее время худшие показатели далеко не такие низкие, как раньше; кроме того, сейчас в командах Главной лиги гораздо меньше хиттеров со средним коэффициентом результативности отбивания 0,150, чем раньше. Гулд утверждает, что общее сокращение разброса — следствие стандартизации или стабилизации.
Когда бейсбол был очень молодым, методы игры еще не стандартизировались настолько, чтобы это могло помешать проделкам лучших игроков. Вилли Килер мог «бить туда, где никого нет» (и набрать средний коэффициент 0,432 в 1897 году), потому что филдеры еще не знали, где им следует находиться. Постепенно игроки осваивали оптимальные методы расстановки на поле, перемещения по нему, подачи и отбивания мяча — и разброс неизбежно сокращался. Сегодня лучшие игроки столкнулись с настолько отточенным под их собственное совершенство противодействием, что это делает невозможным достижение тех высоких результатов, которые были характерны для времен более бессистемной игры. [Выделено автором.]
Иными словами, посредством непрерывной корректировки стратегий в их противостоянии друг с другом система пришла к своему равновесию (Нэша).
Гулд проанализировал статистику хиттинга за десятилетия, чтобы доказать, что сокращение разброса действительно происходит, за исключением единичных «выбросов». В действительности такие «выбросы» подтверждают эту гипотезу, поскольку происходят вскоре после нарушения равновесия под влиянием внешних изменений. Каждый раз при изменении правил игры (зона страйка увеличивается или уменьшается, уменьшается высота питчерской горки или увеличивается количество команд) или технологии (используется более упругий мяч или наконец разрешат алюминиевые биты) сложившаяся система взаимных наилучших ответов выходит из равновесия. И на какое-то время, пока игроки экспериментируют, разброс значений их показателей увеличивается и некоторые из них добиваются успеха, тогда как другие терпят неудачу. В конечном счете равновесие восстанавливается, а разброс снова сокращается. Именно этого и следует ожидать в рамках обучения и корректировки в сторону равновесия Нэша.
В книге Майкла Льюиса Moneyball (по которой впоследствии был снят фильм «Человек, который изменил все» с Брэдом Питтом в главной роли) приведен похожий пример движения к равновесию в бейсболе, однако вместо акцента на стратегиях отдельных игроков он сосредоточен на административных стратегиях команды в отношении найма игроков. В книге рассказывается о решении главного менеджера команды Oakland Athletics использовать при найме игроков так называемую саберметрику, то есть уделять пристальное внимание бейсбольной статистике, основанной на теории максимизации засчитанных очков за пробежки и минимизации очков, проигранных сопернику. Такие решения подразумевали необходимость обращать больше внимания на недооцененную на рынке способность игроков зарабатывать очки. Считается, что именно эти решения сделали Oakland Athletics очень сильной командой, вышедшей в плей-офф в пяти из семи сезонов, несмотря на то что фонд ее заработной платы был меньше половины фонда заработной платы более богатых команд, таких как New York Yankees. Инновационные стратегии найма игроков и формирования фонда заработной платы впоследствии взяли на вооружение другие команды, в частности Boston Red Sox, которая под руководством Тео Эпштейна разрушила «проклятие Бамбино» в 2004 году, выиграв Мировую серию впервые за 86 лет. На протяжении десятилетия почти в дюжине команд было решено нанять специалиста по саберметрике на полную ставку. В сентябре 2011 года Билли Бин посетовал, что ему снова приходится бороться в невыгодных условиях против более крупных команд, научившихся находить наилучшие ответы на его стратегии. В реальных играх часто внедряются инновации, за которыми следует постепенное схождение к равновесию. Приведенные выше примеры из бейсбола подтверждают этот факт, хотя порой на полное схождение к равновесию могут уйти годы, а то и десятилетия.
Мы рассмотрим дополнительные сведения о других прогнозах, основанных на теории игр, в соответствующих разделах следующих глав. К настоящему моменту представленные выше экспериментальные и эмпирические данные должны выработать у вас осторожный оптимизм по отношению к использованию равновесия Нэша, особенно в качестве первого подхода. В целом мы убеждены, что вы сможете достаточно уверенно применять концепцию равновесия Нэша в случаях многократного проведения игры между игроками, составляющими достаточно устойчивую совокупность, при относительно неизменных правилах и условиях. В случае новой игры или игры, разыгрываемой только один раз, с неопытными игроками, концепцию равновесия следует использовать более осмотрительно; при этом для вас не должен стать неожиданностью тот факт, что исход игры окажется не тем равновесием, на которое вы рассчитали. Но даже тогда вашим первым шагом в процессе анализа игры должен быть поиск равновесия Нэша. Это позволит определить, возможен ли такой исход игры, и если нет, выполнить следующий шаг — выяснить причину. Зачастую она кроется в вашем неправильном понимании целей игроков, а не в их неспособности вести игру правильно с учетом своих истинных целей.
Резюме
Когда участники игры с одновременными ходами могут делать выбор из непрерывного диапазона возможных действий, анализ наилучших ответов приводит к формированию правил наилучших ответов, одновременное решение которых позволит определить стратегии равновесия Нэша. Правила наилучших ответов можно отобразить на графике, на котором пересечение двух линий представляет собой равновесие Нэша. Компании, выбирающие цены или количество из большого диапазона возможных значений, или политические партии, выбирающие объемы рекламных расходов, — примеры игр с непрерывными стратегиями.
Теоретические замечания в адрес концепции равновесия Нэша гласят, что она неадекватно учитывает риск, что от нее мало пользы, поскольку во многих играх присутствует множество равновесий Нэша, и что ее невозможно обосновать только рациональностью. Во многих случаях более полное описание игры и ее структуры выигрышей или уточнение самой концепции равновесия Нэша может привести к составлению более точных прогнозов или уменьшению количества возможных равновесий. Концепция рационализации основана на исключении стратегий, которые не могут быть наилучшим ответом, для получения совокупности рационализируемых исходов. Когда в игре есть равновесие Нэша, этот исход будет рационализируемым, однако рационализация позволяет спрогнозировать равновесные исходы и в играх, где равновесие Нэша отсутствует.
Согласно результатам лабораторных экспериментов с концепцией равновесия Нэша, координация в играх со множеством равновесий Нэша в значительной мере зависит от наличия общего культурного опыта. Повторное проведение некоторых игр показывает, что игроки учатся в процессе накопления опыта и со временем начинают выбирать стратегии, максимально близкие к равновесию Нэша. Кроме того, прогнозы равновесий точны только в случае, если исходные предположения экспериментатора соответствуют истинным предпочтениям игроков. Практическое применение теории игр помогло экономистам и политологам понять ряд важных аспектов поведения потребителей, компаний, избирателей, а также законодательных и правительственных органов.
Ключевые термины
График наилучших ответов
Непрерывные стратегии
Правила наилучших ответов
Равновесие квантильных откликов
Рационализация
Рационализируемые стратегии
Стратегии, которые не могут быть наилучшим ответом
Уточнения
Упражнения с решениями
S1. В игре с политической рекламой, о которой шла речь в , партия Л выбирает рекламный бюджет в размере x (миллионов долларов), а партия П — в размере y (миллионов долларов). Мы показали, что правила наилучших ответов в этой игре таковы: 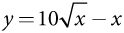 для партии П и
для партии П и 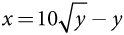 для партии Л.
для партии Л.
a) Каким будет наилучший ответ партии П, если партия Л потратит на рекламу 16 миллионов долларов?
Используйте указанные выше правила наилучших ответов для подтверждения того, что рекламные бюджеты, обеспечивающие равновесие Нэша, составляют: x = y = 25, или 25 миллионов долларов.
S2. В игре с ценообразованием в ресторанах, представленной на , функции потребительского спроса на блюда в ресторанах Xavier’s (Qx) и Yvonne’s (Qy) определены как Qx = 44 – 2Px + Py и Qy = 44 – 2Py + Px. Кроме того, прибыль каждого ресторана зависит от затрат на обслуживание каждого клиента. Предположим, ресторану Yvonne’s удастся их сократить до 2 долларов на одного клиента, полностью отказавшись от официантов (клиенты сами выбирают блюда у стойки, а несколько оставшихся работников убирают посуду со столов). Ресторан Xavier’s по-прежнему несет расходы в размере 8 долларов на одного клиента.
a) Вычислите заново правила наилучших ответов и цены в соответствии с равновесием Нэша для этих двух ресторанов с учетом изменения объема затрат.
b) Постройте график двух кривых наилучших ответов и опишите различия между ним и графиком, представленным на . В частности, какая линия сместилась, куда и насколько? Объясните почему.
S3. В Яппи-Тауне два продуктовых магазина: La Boulangerie, который продает хлеб, и La Fromagerie, который торгует сыром. Производство буханки хлеба обходится в 1 доллар, а фунта сыра — в 2 доллара. Если цена La Boulangerie составляет P1 долларов за буханку хлеба, а La Fromagerie — P2 доллара за фунт сыра, то их недельные объемы продаж, Q1 буханок хлеба и Q2 фунтов сыра, описываются следующими уравнениями:
Q1 = 14 – P1 – 0,5P2, Q2 = 9 – 0,5P1 – P2.
a) Запишите прибыль каждого магазина как функцию P1 и P2 (в следующих упражнениях мы для краткости будем называть ее функцией прибыли). Затем установите соответствующие правила наилучших ответов. Постройте график кривых наилучших ответов и определите цены, соответствующие равновесию Нэша в этой игре.
b) Предположим, оба магазина вступят в сговор и совместно установят цены, позволяющие максимизировать общую сумму своих прибылей. Определите эти цены.
c) Дайте короткое интуитивное объяснение различий между ценами в случае равновесия Нэша и ценами, максимизирующими общую прибыль. Почему максимизация общей прибыли не является равновесием Нэша?
d) В данной задаче хлеб и сыр — взаимодополняющие продукты. Их часто потребляют вместе; именно поэтому снижение цены одного продукта приводит к увеличению объема продаж другого. В ресторанах из примера, приведенного в , используются взаимозаменяющие продукты. Как это различие объясняет разницу между вашими выводами в отношении правил наилучших ответов, цен в равновесии Нэша и цен, максимизирующих общую прибыль?
S4. В игре на есть единственное равновесие Нэша в чистых стратегиях. Тем не менее все девять ее исходов будут рационализируемыми. Обоснуйте это утверждение, объясняя логику своих рассуждений по каждому исходу.
S5. Перечислите рационализруемые стратегии каждого игрока в игре, представленной в . Объясните логику своих рассуждений.
S6. В данной главы анализируется игра в рыбную ловлю, разыгрываемая в небольшом прибрежном городке. После определения правил наилучших ответов двух лодок можно использовать концепцию рационализации для обоснования равновесия Нэша в данной игре. В ее описании процесс сокращения количества стратегий, которые не могут быть наилучшим ответом, сводится к трем циклам. К третьему циклу мы знаем, что R (количество бочек рыбы, выловленной лодкой 1) должно составлять минимум 9, а S (количество бочек рыбы, выловленной лодкой 2) — минимум 4,5. Процесс сокращения в ходе этого цикла ограничил значения R диапазоном от 9 до 12,75, а значения S — диапазоном от 4,5 до 7,5. Выполните еще один (четвертый) цикл сокращений и покажите полученные к его концу диапазоны значений R и S.
S7. Две тележки для торговли кокосовым молоком (из кокосового ореха) находятся в местах 0 и 1 в одной миле друг от друга на пляже в Рио-де-Жанейро. (На этом пляже кокосовое молоко продают только эти две тележки.) Тележки 0 и 1 назначают цену за каждый кокос p0 и p1 соответственно. Кокосовое молоко покупает тысяча отдыхающих, равномерно распределенных вдоль пляжа между тележками 0 и 1. В течение одного дня, проведенного на пляже, один отдыхающий покупает одну порцию кокосового молока. Помимо цены каждый отдыхающий несет транспортные издержки в размере 0,5 × d2 где d — расстояние (в милях) от его пляжного места до кокосовой тележки. В данной системе тележка 0 продает кокосовое молоко всем отдыхающим, находящимся между точками 0 и x, а тележка 1 — всем отдыхающим между точками x и 1, где x — это местоположение отдыхающего, который платит одну и ту же общую цену, куда бы он ни отправился — к тележке 0 или к тележке 1. В таком случае местоположение точки x описывает следующая формула:
p0 + 0,5x2 = p1 + 0,5(1 – x)2.
Две тележки установят цены таким образом, чтобы максимизировать свои показатели чистой прибыли B; прибыль зависит от дохода (цена, установленная тележкой, умноженная на количество покупателей) и издержек (каждая тележка несет издержки в размере 0,25 доллара на один кокос, умноженные на количество проданных кокосов).
a) Выведите для каждой тележки формулу, описывающую количество обслуженных покупателей как функцию от p0 и p1. (Помните, что тележка 0 обслуживает покупателей, находящихся между точками 0 и x, то есть просто x, а тележка 1 обслуживает покупателей между точками x и 1, или 1 – x. Иными словами, тележка 0 продает кокосовое молоко x покупателям, а тележка 1 (1 – x) покупателям, где x и (1 − х) исчисляются в тысячах.)
b) Запишите функции прибыли для двух тележек. Определите правила наилучших ответов для обеих тележек как функцию от цены конкурента.
c) Постройте график правил наилучших ответов, а затем вычислите (и покажите на графике) соответствующий равновесию Нэша уровень цен на кокосовое молоко, продающееся на пляже.
S8. Нефть транспортируется по всему миру в танкерах класса VLCC (водоизмещением свыше 160 тысяч тонн). По состоянию на 2001 год более 92 процентов всех танкеров класса VLCC были построены в Южной Корее и Японии. Допустим, цена новых танкеров VLCC (в миллионах долларов) определяется функцией P = 180 – Q , где Q — количество построенных танкеров, Q = qКорея + qЯпония. (То есть будем исходить из того, что такие танкеры выпускают только в Японии и Корее, стало быть, они образуют дуополию.) Предположим, затраты на строительство каждого танкера составляют 30 миллионов долларов как в Корее, так и в Японии. Иначе говоря, cКорея = cЯпония = 30, где затраты на один танкер измеряются в миллионах долларов.
a) Запишите функции прибыли для каждой из двух стран, выраженные через qКорея и qЯпония, а также либо cКорея, либо cЯпония. Найдите функцию наилучшего ответа каждой страны.
b) С помощью функций наилучших ответов, вычисленных в пункте а, отыщите соответствующее равновесию Нэша количество танкеров класса VLCC, выпускаемых каждой страной в год. Какова цена танкера VLCC? Какую прибыль получает каждая страна?
c) Затраты на оплату труда на корейских верфях существенно ниже, чем на японских. Теперь предположим, что стоимость строительства одного танкера в Японии составляет 40 миллионов долларов, а в Корее — всего 20 миллионов долларов. Если cКорея = 20, а cЯпония = 40, какова рыночная доля каждой страны (то есть процент танкеров, которые продает каждая страна, от общего количества проданных танкеров)? Какова прибыль каждой страны?
S9. Расширим предыдущую задачу. Предположим, на рынок строительства танкеров класса VLCC решит выйти Китай. Дуополия, соответственно, превратится в триополию, а значит, хотя цена по-прежнему рассчитывается как P = 180 – Q, количество построенных танкеров описывается формулой Q = qКорея + qЯпония + qКитай. Допустим, во всех странах объем затрат на строительство одного танкера составляет 30 миллионов долларов: cКорея = cЯпония = сКитай = 30.
a) Запишите функции прибыли для каждой из трех стран, выраженные через qКорея, qЯпония и qКитай, а также через cКорея, cЯпония или сКитай. Вычислите функцию наилучшего ответа каждой страны.
b) Воспользовавшись решением, полученным в пункте а, определите количество выпущенных танкеров, рыночную долю (см. ) и прибыль каждой страны. Это потребует решения трех уравнений с тремя неизвестными.
c) Как изменится цена одного танкера VLCC в новой триополии по сравнению с дуополией, представленной в ? Почему?
S10. Моника и Нэнси создали деловое товарищество в целях предоставления консультационных услуг в гольф-индустрии. Каждой из них предстоит решить, сколько усилий вкладывать в этот бизнес. Пусть m — это количество усилий, вкладываемых Моникой, а n — Нэнси.
Общая прибыль товарищества рассчитывается по формуле 4m + 4n + mn и исчисляется в десятках тысяч долларов, а партнеры делят ее поровну. Однако партнеры должны по отдельности нести затраты, связанные с вложением усилий; объем этих затрат в случае Моники составляет m2, а в случае Нэнси — n2 (также исчисляются в десятках тысяч долларов). Каждая участница товарищества должна принять решение о количестве усилий, не зная о решении коллеги.
a) Если Моника и Нэнси вложат в бизнес усилия m = n = 1, какой выигрыш получит каждая из них?
b) Если Моника вложит усилия m = 1, каким должен быть наилучший ответ Нэнси?
c) Каково равновесие Нэша в этой игре?
S11. Равновесие Нэша можно получить посредством рационализации в играх с кривыми наилучших ответов, направленными вверх, если циклы исключения стратегий, которые не могут быть наилучшими ответами, начинаются с минимально возможных значений. Рассмотрим игру в ценообразование между ресторанами Xavier’s Tapas Bar и Yvonne’s Bistro, представленную на . Используйте и правила наилучших ответов, на основании которых он получен, чтобы приступить к рационализации равновесия Нэша в этой игре. Начните с самых низких цен в двух ресторанах и опишите (минимум) два цикла сужения совокупности рационализируемых цен до равновесия Нэша.
S12. Профессор предлагает Эльзе и ее 49 однокурсникам сыграть в следующую игру. Все студенты одновременно и втайне друг от друга записывают на листках бумаги число от 0 до 100, после чего сдают листки профессору. Тот подсчитывает Х — среднее чисел, выбранных студентами. Студент, число которого окажется наиболее близким к половине от Х, получает 50 долларов. Если такое число выберут несколько студентов, они делят приз поровну.
a) Докажите, что выбор числа 80 — доминируемая стратегия.
b) Какой была бы совокупность наилучших ответов для Эльзы, если бы она знала, что все однокурсники выберут число 40? То есть каков диапазон чисел, в котором каждое число ближе к выигрышному числу, чем 40?
c) Какой была бы совокупность наилучших ответов для Эльзы, если бы она знала, что все ее однокурсники выберут число 10?
d) Найдите симметричное равновесие Нэша в этой игре. Иными словами, какое число будет наилучшим ответом на выбор всеми остальными игроками одного и того же числа?
e) Какие стратегии в этой игре будут рационализируемыми?
Упражнения без решений
U1. Diamond Trading Company (DTC), дочерняя компания De Beers, — основной поставщик высококачественных алмазов на оптовый рынок. Для простоты предположим, что DTC имеет монополию на оптовую торговлю алмазами. Следовательно, их оптовая цена напрямую зависит от количества алмазов, которое решает продать компания DTC. Пусть оптовую цену алмазов (в сотнях долларов) описывает следующая функция обратного спроса: P = 120 – QDTC , где QDTC — количество продаваемых алмазов. Допустим, DTC несет издержки в размере 12 (сотен долларов) на один алмаз высокого качества.
a) Запишите функцию прибыли DTC, выраженную через QDTC , и вычислите объем поставок алмазов, обеспечивающий DTC максимальную прибыль. Какой будет оптовая цена алмазов при таком объеме поставок? Какова прибыль DTC?
Возмущенные монополией DTC, несколько компаний по добыче алмазов и крупных ретейлеров создали совместное предприятие под названием Adamantia в качестве конкурента DTC на оптовом рынке алмазов. Теперь оптовая цена алмазов определяется по формуле P = 120 – QDTC – QADA. Предположим, Adamantia несет издержки в размере 12 (сотен долларов) на один алмаз высокого качества.
b) Запишите функцию прибыли компаний DTC и Adamantia. Какое количество алмазов поставляет на оптовый рынок каждая из них в случае равновесия? Какую оптовую цену алмазов подразумевает такое количество? Какую прибыль получит каждый поставщик в такой дуополии?
c) Опишите различия между ситуацией на оптовом рынке алмазов в случае дуополии с участием DTC и Adamantia и монополии DTC. Что произойдет с объемом поставок алмазов на рынок и рыночной ценой в связи с выходом на него Adamantia? Что произойдет с совокупной прибылью компаний DTC и Adamantia?
U2. В городе Харкинсвилль есть два кинотеатра: Modern Multiplex, осуществляющий премьерные показы, и Sticky Shoe, демонстрирующий фильмы, вышедшие в прокат ранее, по более низкой цене. Спрос на фильмы в Modern Multiplex описывается формулой QMM = 14 – PMM + PSS, а в Sticky Shoe — формулой QSS = 8 – 2PSS + PMM, где цены измеряются в долларах, а количество — в сотнях кинозрителей. В кинотеатре Modern Multiplex объем затрат на одного зрителя составляет 4 доллара, а в Sticky Shoe — всего 2 доллара.
a) На основании уравнений спроса определите, какие услуги предоставляют кинотеатры Modern Multiplex и Sticky Shoe — взаимозаменяющие или взаимодополняющие.
b) Запишите функцию прибыли каждого кинотеатра, выраженную через PSS и PMM. Определите правило наилучших ответов для каждого кинотеатра.
c) Определите цену, количество и прибыль каждого кинотеатра в соответствии с равновесием Нэша.
d) Какими бы были значения цены и количества для каждого кинотеатра, если бы они вступили в сговор в целях максимизации общей прибыли на этом рынке? Почему исход, основанный на сговоре, не будет равновесием Нэша?
U3. Перенесемся на десять лет в будущее в ситуации, представленной в упражнении S3. Спрос на хлеб и сыр в Яппи-Тауне снизился, и два магазина, La Boulangerie и La Fromagerie, выкупила третья компания — L’Épicerie. Производство буханки хлеба по-прежнему обходится в 1 доллар, а фунта сыра — в 2 доллара, однако количество продаваемого хлеба и сыра (Q1 и Q2 соответственно, в тысячах) теперь описывается следующими уравнениями:
Q1 = 8 – P1 – 0,5P2, Q2 = 16 – 0,5P1 – P2.
Как и прежде, P1 — это цена буханки хлеба в долларах, а P2 — цена фунта сыра в долларах.
a) Поначалу компания L’Épicerie управляет магазинами La Boulangerie и La Fromagerie так, будто это две отдельные компании с независимыми управляющими, каждый из которых пытается максимизировать прибыль своего магазина. Определите количество, цену и прибыль этих двух подразделений L’Épicerie в соответствии с равновесием Нэша с учетом новых уравнений количества продаваемого хлеба и сыра.
b) Владельцы L’Épicerie считают, что могут получить более высокую общую прибыль посредством координации стратегий ценообразования в подразделениях своей компании в Яппи-Тауне. Какова цена хлеба и сыра, максимизирующая общую прибыль, при условии такого сговора? Какое количество каждого продукта продают магазины La Boulangerie и La Fromagerie, и какую прибыль получает каждый из них в отдельности?
c) Почему компании порой продают часть своей продукции по цене ниже себестоимости? Дайте логическое обоснование продажи продукции с убытком, воспользовавшись своим ответом из пункта b в качестве иллюстрации.
U4. Тележки для торговли кокосовым молоком из снова установили на следующий день. Почти все условия прежние: тележки находятся в тех же местах; количество и распределение отдыхающих такое же; спрос тоже не изменился — одна порция кокосового молока. Единственное отличие — это неимоверно жаркий день, поэтому каждый отдыхающий несет более высокие транспортные издержки в размере 0,6 × d2. Как и прежде, тележка 0 продает кокосовое молоко всем отдыхающим, находящимся между точками 0 и x, а тележка 1 — всем отдыхающим между точками x и 1, где x — это местоположение отдыхающего, который платит одну и ту же общую цену, куда бы он ни отправился — к тележке 0 или 1. Однако теперь местоположение точки x определяется выражением
p0 + 0,6x2 = p1 + 0,6(1 – x)2.
Каждая тележка продолжает нести издержки в размере 0,25 доллара на один проданный кокос.
a) Для каждой тележки выведите формулу, описывающую количество обслуженных покупателей как функцию от p0 и p1. (Не забывайте, что тележка 0 обслуживает покупателей, находящихся между точками 0 и x, то есть просто x, а тележка 1 — между точками x и 1, или 1 – x. Иными словами, тележка 0 продает кокосовое молоко x покупателям, а тележка 1 — (1 – x) покупателям, где x и (1 – х) исчисляются в тысячах.)
b) Запишите функции прибыли для двух тележек и определите для них правила наилучших ответов.
c) Вычислите соответствующий равновесию Нэша уровень цен на кокосовое молоко, продающееся на пляже. Как эта цена отличается от цены, рассчитанной в упражнении S7? Почему?
U5. В игре, представленной на , есть единственное равновесие Нэша в чистых стратегиях. Найдите его и покажите, что оно будет также рационализируемым исходом данной игры.
U6. Найдите рационализируемые стратегии игры «чет или нечет» из .
U7. В игре с рыболовными лодками в мы показали, как может сложиться ситуация, когда единственный рационализируемый исход в непрерывных стратегиях представляет собой также и равновесие Нэша. Тем не менее так бывает не всегда: может существовать множество рационализируемых стратегий, и не все из них обязательно будут частью равновесия Нэша.
Вернувшись к игре в политическую рекламу из , найдите совокупность рационализируемых стратегий для партии Л. (Учитывая симметричные выигрыши двух партий, совокупность рационализируемых стратегий будет такой же и для партии П.)
U8. Компании Intel и AMD, основные производители центральных процессоров, конкурируют друг с другом в категории микросхем (чипов) средней производительности (среди прочих категорий). Предположим, что мировой спрос на такие чипы зависит от их количества, выпускаемого двумя компаниями, а значит цена (в долларах) микросхем средней производительности определяется по формуле P = 210 – Q, где Q = qIntel + qAMD — количество микросхем, исчисляемое в миллионах. Производство каждого чипа обходится Intel в 60 долларов. В AMD процесс производства организован лучше, поэтому ей производство каждой микросхемы обходится в 48 долларов.
a) Запишите функцию прибыли каждой компании, выраженную через qIntel и qAMD. Определите правило наилучших ответов каждой компании.
b) Вычислите цену, количество и прибыль каждой компании в соответствии с равновесием Нэша.
c) (дополнительное упражнение). Предположим, Intel приобрела AMD и теперь имеет два подразделения с разными производственными затратами. Компания, образовавшаяся в результате поглощения, стремится максимизировать общую прибыль двух подразделений. Сколько микросхем должно производить каждое подразделение? (Подсказка: возможно, вам придется хорошенько поразмышлять над этой задачей, а не слепо применять математические методы.) Какова рыночная цена и совокупная прибыль компании?
U9. Вернемся к игре с триополией на рынке танкеров класса VLCC из . В действительности у этих стран не одинаковые издержки производства. Китай постепенно, в течение нескольких лет, выходит на этот рынок, и из-за отсутствия опыта его издержки производства с самого начала были достаточно высокими.
a) Определите количество, рыночную цену и прибыль участников триополии в случае, когда затраты на один танкер составляют 20 миллионов долларов в Корее, 40 миллионов долларов в Японии и 60 миллионов долларов в Китае (cКорея = 20, cЯпония = 40, cКитай = 60).
После того как Китай накопит больше опыта и увеличит производственные мощности, его издержки производства существенно сократятся. Поскольку в Китае рабочая сила еще дешевле, чем в Корее, в конечном счете затраты на строительство одного танкера станут в Китае даже меньше, чем в Корее.
b) Выполните то же задание, что и в пункте а, но с условием, что затраты Китая на один танкер составляют 16 миллионов долларов (cКорея = 20, cЯпония = 40, cКитай = 16).
U10. Вернемся к истории Моники и Нэнси из . После дополнительной профессиональной подготовки Моника более эффективно выполняет работу, поэтому теперь общая прибыль их компании рассчитывается по формуле 5m + 4n + mn в десятках тысяч долларов. Как и прежде, m — количество усилий, вкладываемых в бизнес Моникой, а n — Нэнси; затраты обеих составляют m2 и n2 соответственно (в тысячах долларов).
Условия партнерства по-прежнему требуют разделения прибыли поровну, несмотря на то, что Моника более продуктивна. Предположим, Моника и Нэнси принимают решения о вложении усилий одновременно.
a) Каким должен быть наилучший ответ Моники в случае, если, по ее оценкам, Нэнси будет вкладывать усилия в размере n = 4/3?
b) Найдите равновесие Нэша в этой игре.
c) По сравнению с равновесием Нэша, найденным в , Моника вкладывает больше, меньше или столько же усилий? Что можно сказать о Нэнси?
d) Каковы итоговые выигрыши Моники и Нэнси в новом равновесии Нэша (после разделения общей прибыли с учетом затрат на вложенные усилия)? Как они отличаются от выигрышей обеих при прежнем равновесии Нэша? Кто в конечном счете получает большую выгоду от дополнительной подготовки Моники?
U11. Профессор предлагает Эльзе и ее 49 однокурсникам сыграть в новую игру. Как и прежде, все студенты одновременно и втайне друг от друга записывают на листках бумаги число от 0 до 100, после чего профессор вычисляет среднее выбранных чисел и обозначает его символом X. На этот раз студент, число которого окажется наиболее близким к 2/3 × (X + 9), получит 50 долларов. Если такое число выберут несколько студентов, они разделят приз поровну.
a) Найдите симметричное равновесие Нэша в этой игре. То есть какое число станет наилучшим ответом на выбор всеми остальными игроками одного и того же числа?
b) Докажите, что выбор числа 5 — это доминируемая стратегия. (Подсказка: каким должно быть среднее значение X для всей группы, чтобы ожидаемое число было равно 5?)
c) Докажите, что выбор числа 90 — это доминируемая стратегия.
d) Определите все доминируемые стратегии.
e) Предположим, Эльза убеждена, что никто из ее однокурсников не выберет доминируемые стратегии, найденные в пункте d. Учитывая эти убеждения, какие стратегии не могут быть наилучшими ответами для Эльзы?
f) Какие стратегии в этой игре рационализируемые? Объясните логику ваших рассуждений.
U12 (дополнительное упражнение, требующее вычислений). Вспомните игру с политической рекламной кампанией партий Л и П из . В ней, когда партия Л тратит на рекламу x миллионов долларов, а партия R — y миллионов долларов, Л получает долю голосов x / (x + y) , а П — y / (x + y) . Мы также упоминали, что в такой модели может возникнуть два типа асимметрий между партиями. У одной партии (скажем, П) может быть возможность размещать рекламу по более низкой цене, или рекламный бюджет партии П может оказаться более эффективным с точки зрения привлечения голосов избирателей по сравнению с бюджетом партии Л. Для того чтобы учесть обе возможности, мы можем записать функции выигрышей двух партий следующим образом:
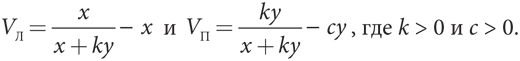
Эти функции выигрышей показывают, что у партии П есть преимущество в плане относительной эффективности ее рекламы при высоком значении k и при низком значении c.
a) Используйте эти функции выигрышей для получения функций наилучших ответов для партии П (которая выбирает y) и Л (которая выбирает x).
b) С помощью калькулятора или компьютера постройте график этих функций наилучших ответов при k = 1 и c = 1. Какой результат обеспечивает преимущество в отношении затрат на рекламу?
c) Сравните график из пункта b при k = 1 и c = 1 с графиком при k = 2 и c = 1. Какой результат обеспечивает преимущество в плане эффективности рекламного бюджета?
d) Найдите решения по функциям наилучших ответов, которые вы определили в пункте а, для x и y, чтобы показать, что расходы на рекламные кампании в случае равновесия Нэша составляют
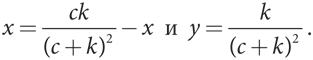
e) Пусть k = 1 в равновесных уравнениях уровней расходов. Покажите, как эти два равновесных уровня расходов меняются в зависимости от значения c (то есть объясните знаки dx / dc и dy / dc). Тогда пусть c = 1; покажите, как эти два равновесных уровня расходов меняются в зависимости от значения k (то есть объясните знаки dx / dk и dy / dk). Подтверждают ли ваши ответы результаты, полученные вами в пунктах b и c данного упражнения?

