4 Игры с одновременными ходами: дискретные стратегии
Игрой с одновременными ходами, как пояснялось в , считается игра, в которой игроки делают ходы, не зная о выборе соперников. Очевидно, что такая ситуация складывается в случае, когда игроки действуют одновременно, а также когда они выбирают действия обособленно, не располагая информацией о действиях других игроков, даже если этот выбор делается в разное время. (Именно поэтому в играх с одновременными ходами имеет место несовершенная информация в том смысле, о котором мы говорили в .) Эта глава посвящена играм, в которых присутствует только одновременное взаимодействие между игроками. Мы рассмотрим различные типы игр с одновременными ходами, опишем концепцию их решения под названием «равновесие Нэша» и проанализируем игры без, с одним и несколькими равновесиями.
К категории игр с одновременными ходами можно отнести многие из знакомых вам стратегических ситуаций. Различные производители телевизоров, стереосистем или автомобилей принимают решения о дизайне и свойствах продукта, не зная о контраргументах конкурентов. Избиратели на выборах одновременно отдают свои голоса, не зная о предпочтениях других избирателей. В футболе взаимодействие между вратарем и нападающим противника во время пенальти требует одновременного решения обоих: вратарь не может себе позволить ждать удара по мячу, чтобы определить его траекторию, поскольку тогда уже будет слишком поздно.
Очевидно, что при выборе действия участник игры с одновременными ходами не располагает информацией о решениях других игроков. Кроме того, он не может предвидеть их реакцию на его выбор, так как они тоже действуют вслепую по отношению к нему. Поэтому каждый игрок должен анализировать предполагаемые шаги соперников, а те, в свою очередь, проводить аналогичный встречный анализ. Такая цикличность несколько усложняет анализ игр с одновременными ходами по сравнению с анализом игр с последовательными ходами, но выполнить его не так уж трудно. В этой главе мы сформулируем для этих игр простую концепцию равновесия, обладающую значительной пояснительной и прогностической способностью.
1. Описание игр с одновременными ходами и дискретными стратегиями
В и мы неоднократно подчеркивали, что стратегия — это исчерпывающий план действий. Однако в чистых играх с одновременными ходами у каждого участника есть максимум одна возможность действовать (хотя такое действие может состоять из множества компонентов), поскольку если бы их было несколько, это был бы уже элемент игры с последовательными ходами. Стало быть, в играх с одновременными ходами нет никаких реальных различий между стратегией и действием, поэтому в данном контексте эти термины часто используются как синонимы. Существует только одна сложность. Стратегия может представлять собой вероятностный выбор из первоначально оговоренных базовых действий. Например, в спорте игрок или команда могут умышленно выбирать действия в случайном порядке, чтобы соперник был вынужден угадывать. Такие вероятностные стратегии называются смешанными и рассматриваются в . Сейчас же мы ограничимся анализом базовых, первоначально оговоренных действий, обозначаемых термином чистые стратегии.
Во многих играх у каждого игрока есть конечное количество дискретных чистых стратегий, например дриблинг, пас и бросок в баскетболе, тогда как в ряде других игр чистая стратегия игрока может представлять собой любое число из непрерывного диапазона значений, скажем цену, назначаемую компанией на свой продукт. Это различие никак не влияет на общую концепцию равновесия в играх с одновременными ходами, но связанные с такими играми идеи легче формулировать с помощью дискретных стратегий; решение игр с непрерывными стратегиями требует несколько более продвинутых инструментов. Поэтому в данной главе мы ограничимся анализом более простых чистых дискретных стратегий, а стратегии с непрерывными переменными рассмотрим в .
Игры с одновременными ходами и дискретными стратегиями чаще всего описывают с помощью таблицы игры (синонимы: матрица игры или таблица выигрышей), которая называется нормальной или стратегической формой игры. Таблица игры позволяет проиллюстрировать игру с любым количеством участников, однако ее размерность должна соответствовать их числу. В случае игры с двумя участниками таблица имеет два измерения, а заголовки строк и столбцов в ней — это стратегии, находящиеся в распоряжении первого и второго игроков. Следовательно, размер таблицы зависит от количества доступных игрокам стратегий. В ячейках указываются выигрыши, которые получат игроки при подобающей конфигурации стратегий. Игры с тремя участниками требуют трехмерной таблицы; ее мы рассмотрим далее в этой главе.
Концепция таблицы выигрышей для простой игры приведена на рис. 4.1. Представленная на нем игра не имеет специальной интерпретации, поэтому мы можем сформулировать концепции, не отвлекаясь на ее «историю». Имена участников игры — Строка и Столбец. В распоряжении Строки находится четыре варианта выбора (стратегий или действий), обозначенных как «вверху», «высоко», «низко», «внизу», а Столбца — три варианта: «слева», «посредине» и «справа». Каждый выбор Строки и Столбца определяет возможный исход игры. Выигрыши, связанные с каждым исходом игры, показаны в ячейке, соответствующей данной строке и данному столбцу. Принято считать, что из двух чисел, отображающих выигрыши, первое число отвечает выигрышу Строки, а второе — выигрышу Столбца. Например, если Строка выберет вариант «высоко», а Столбец — «справа», выигрыши составят 6 в случае Строки и 4 в случае Столбца. Для дополнительного удобства мы выделяем все, что касается Строки (имя игрока, его стратегии и выигрыши), черным цветом, а Столбца — серым .
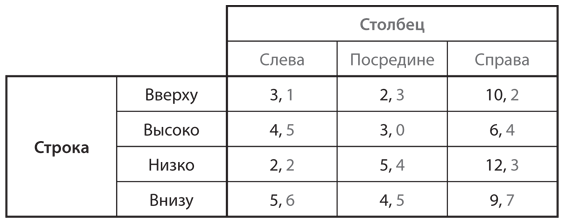
Рис. 4.1. Представление игры с одновременными ходами в виде таблицы
Далее рассмотрим второй пример игры с более содержательной историей. На рис. 4.2 представлена упрощенная версия одного розыгрыша в американском футболе. Нападающие пытаются продвинуть мяч вперед, чтобы повысить шансы забить филд-гол. У них есть четыре возможные стратегии: пробежка и три паса разной длины (короткий, средний и длинный). Чтобы сдерживать атаку, защитники могут использовать одну из трех стратегий: защита в случае пробежки и в случае паса и блиц против квотербека. Нападающие пытаются набрать как можно больше ярдов, тогда как защитники — помешать им это сделать. Предположим, у нас достаточно информации об основных сильных сторонах тех и других, для того чтобы оценить вероятность завершения различных розыгрышей и определить среднее количество набранных ярдов, которого можно было бы ожидать при каждой комбинации стратегий. Например, когда команда нападения выбирает стратегию «средний пас», а команда защиты отвечает стратегией «защита в случае паса», по нашим оценкам, выигрыш нападения составляет 4,5 набранных ярда, или +4,5. «Выигрыш» защиты — 4,5 потерянных ярда, или −4,5. В других ячейках также показаны наши оценки количества ярдов, набранных или потерянных каждой командой.
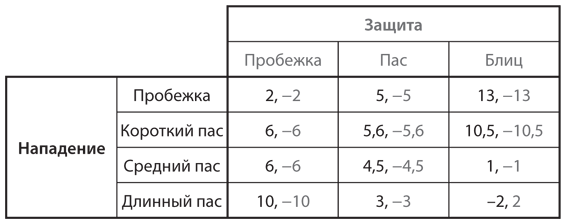
Рис. 4.2. Один розыгрыш в американском футболе
Обратите внимание, что сумма выигрышей в каждой ячейке таблицы равна 0: когда нападающие набирают 5 ярдов, защитники теряют 5 ярдов, и наоборот: когда нападающие теряют 2 ярда, защитники набирают 2 ярда. Такая схема достаточно широко распространена в спорте, где интересы двух сторон прямо противоположны друг другу. Как отмечалось в , мы называем это игрой с нулевой (или иногда с постоянной) суммой. Вы должны помнить, что, согласно определению, игра с нулевой суммой представляет собой игру, в которой сумма выигрышей во всех ячейках постоянная величина, будь то 0, 6 или 1000. (В описывается игра, в которой сумма выигрышей двух игроков составляет 100.) Основная особенность игры с нулевой суммой состоит в том, что проигрыш одного игрока равен выигрышу другого.
2. Равновесие Нэша
Для анализа игр с одновременными ходами необходимо рассмотреть, как игроки выбирают действия. Вернемся к игре, представленной на . Обратите внимание на тот ее исход, при котором Строка выбирает вариант «низко», а Столбец — «посредине», с выигрышами 5 для Строки и 4 для Столбца. Каждый игрок отдает предпочтение действию, которое обеспечит ему более высокий выигрыш, и при данном исходе делает такой выбор с учетом выбора соперника. Если Строка выбирает вариант «низко», может ли Столбец получить более высокий выигрыш, выбрав что-то другое, а не «посредине»? Нет, поскольку вариант «слева» обеспечивает ему выигрыш 2, а вариант «справа» — выигрыш 3 и оба не превышают выигрыш 4 в случае варианта «посредине». Стало быть, стратегия «посредине» — наилучший ответ Столбца на стратегию «низко», реализуемую Строкой. С другой стороны, если Столбец остановится на варианте «посредине», получит ли Строка более высокий выигрыш, предпочтя варианту «низко» какой-нибудь иной? И снова нет, потому что выигрыши от выбора варианта «вверху» (2), «высоко» (3) или «внизу» (4) не будут больше выигрыша Строки в случае выбора варианта «низко» (5). Следовательно, «низко» — наилучший ответ Строки на стратегию «посредине», применяемую Столбцом.
Эти два варианта выбора, «низко» для Строки и «посредине» для Столбца, представляют собой наилучший ответ игрока, сделавшего соответствующий выбор, на действие другого игрока. После такого выбора оба игрока не захотели бы по собственной инициативе переключаться на что-либо другое. Согласно определению некооперативной игры, игроки делают выбор независимо друг от друга; следовательно, такие односторонние изменения — все, что может предпринять каждый игрок. Но поскольку ни один из них к ним не склонен, было бы естественно называть данное положение вещей равновесием. В этом и состоит суть концепции равновесия Нэша.
Согласно несколько более формальной формулировке, равновесие Нэша в игре представляет собой перечень стратегий (по одной на каждого участника), при котором ни один игрок не может увеличить выигрыш, выбрав другую стратегию из имеющихся в его распоряжении, если другие игроки придерживаются стратегий, оговоренных в этом перечне.
А. Дальнейшее разъяснение концепции равновесия Нэша
Для того чтобы лучше понять концепцию равновесия Нэша, давайте еще раз проанализируем игру на . Возьмем какую-либо другую ячейку вместо ячеек «низко», «посредине», например ячейку, в которой Строка выбирает вариант «высоко», а Столбец — «слева». Может ли это сочетание стратегий быть равновесием Нэша? Нет, потому что, если Столбец применит стратегию «слева», Строка при выборе стратегии «внизу» вместо «высоко», которая обеспечивает выигрыш 4, получит более высокий выигрыш 5. Точно так же сочетание стратегий «внизу», «слева» не будет равновесием Нэша, поскольку Столбец может извлечь больше выгоды, перейдя на стратегию «справа» и тем самым увеличив свой выигрыш с 6 до 7.
Определение равновесия Нэша не требует, чтобы равновесные варианты выбора обязательно были лучше всех имеющихся вариантов. На рис. 4.3 отображена та же ситуация, что и на , за одним исключением: выигрыш Строки от стратегий «внизу», «посредине» изменился на 5, то есть стал таким же, как и для стратегий «низко», «посредине». По-прежнему верно то, что при выборе Столбцом варианта «посредине» Строка не может добиться большего, чем в случае выбора варианта «низко». Следовательно, ни у одного игрока нет оснований для изменения действия в результате исхода «низко», «посредине», что позволяет квалифицировать данный исход как равновесие Нэша.
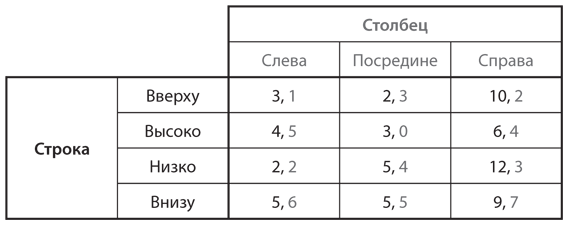
Рис. 4.3. Вариант игры, представленной на , с равными выигрышами
Однако важно учесть, что равновесие Нэша не всегда оптимально для обоих игроков. На пара стратегий «внизу», «справа» обеспечивает выигрыши 9, 7, которые лучше для обоих игроков, чем выигрыши 5, 4 при равновесии Нэша. Тем не менее, играя независимо друг от друга, игроки не смогут придерживаться именно этих стратегий. Если Столбец предпочтет вариант «справа», Строка может захотеть заменить вариант «внизу» на «низко» и выиграть 12 вместо 9. Получение выигрышей 9, 7 потребует кооперативного действия, которое сделало бы такой «обман» невозможным. Мы рассмотрим данный тип поведения чуть ниже (и более подробно в ), а пока просто хотим указать на тот факт, что равновесие Нэша может не соответствовать общим интересам игроков.
Чтобы закрепить понимание концепции равновесия Нэша, давайте еще раз посмотрим на , отображающий игру в американский футбол. Если защита выберет стратегию «защита в случае паса», то лучший вариант для нападающих — «короткий пас» (выигрыш 5,6 против 5, 4,5 или 3). И наоборот, если команда нападения предпочтет вариант «короткий пас», то лучший вариант для защиты — «защита в случае паса», которая позволит команде нападения набрать всего 5,6 ярда, тогда как при выборе вариантов «защита в случае пробежки» и «блиц» команда защиты уступила бы 6 и 10,5 ярда соответственно. (Не забывайте, что записи в каждой ячейке таблицы игры с нулевой суммой — это выигрыши игрока под именем Строка, поэтому самый лучший вариант выбора для Столбца — тот, который обеспечивает самый низкий, а не самый высокий показатель.) В данной игре сочетание стратегий «короткий пас», «защита в случае паса» — это равновесие Нэша, а полученный выигрыш команды нападения составляет 5,6 ярда.
Как вычислить равновесие Нэша в играх? Для этого можно проверить каждую ячейку на наличие стратегий, удовлетворяющих равновесию Нэша. Такой систематический анализ надежен, но утомителен, за исключением случаев, когда он выполняется в контексте простых игр или с помощью хорошей компьютерной программы. К счастью, существуют и другие методы, применимые к особым типам игр, которые позволяют не только быстро отыскать равновесие Нэша, но и лучше понять процесс размышлений, посредством которого формируются убеждения, а затем и выбор. Мы проанализируем эти методы в следующих разделах.
Б. Равновесие Нэша как система убеждений и выбор вариантов
Прежде чем приступать к дальнейшему изучению и применению концепции равновесия Нэша, попробуем прояснить то, что, возможно, тревожит некоторых из вас. Мы сказали, что в равновесии Нэша каждый игрок выбирает свой лучший ответ на выбор другого игрока. Но выбор делается одновременно. Тогда как игрок может реагировать на то, что еще не произошло, или по крайней мере не зная, что именно произошло?
Люди постоянно играют в игры с одновременными ходами и делают свой выбор. Для этого им необходимо найти замену фактическим знаниям или наблюдениям за действиями других игроков. Игроки могут делать слепые догадки и рассчитывать на то, что они окажутся ниспосланными свыше, но, к счастью, существуют более эффективные способы выяснить, что предпринимают другие. Один из них — опыт и наблюдение: если игроки постоянно играют в данную игру или аналогичные игры с подобными игроками, у них может сформироваться неплохое представление об их предпочтениях. В этом случае не самые лучшие варианты выбора вряд ли продержатся долго. Еще один способ — логический процесс мышления через размышления других игроков. Вы ставите себя на их место и размышляете о том, о чем они думают; разумеется, они тоже ставят себя на ваше место и размышляют о том, что думаете вы. На первый взгляд такая логика кажется циклической, однако есть несколько способов вмешаться в этот цикл, и мы покажем их на конкретных примерах в следующих разделах. Равновесие Нэша можно считать кульминацией такого процесса размышлений, в ходе которого каждый игрок правильно определил выбор других игроков.
Посредством наблюдения, или логической дедукции, или какого-либо иного подхода вы как участник игры формируете некоторое представление о выборе участников игр с одновременными ходами. Найти слова для описания этого процесса или его результатов не так уж легко. Речь идет не о предвидении и не о прогнозировании, поскольку действия других игроков выполняются одновременно с вашими и не относятся к будущему. Специалисты по теории игр чаще всего используют термин убеждение. Он не идеален для обозначения происходящего, поскольку вызывает смысловые ассоциации с уверенностью или определенностью в большей степени, чем следовало бы (в мы допустим возможность того, что убеждения могут быть сопряжены с некоторой неопределенностью), однако ввиду отсутствия более подходящего обозначения нам придется им довольствоваться.
Концепция убеждения соотносится также с описанием неопределенности, представленным в , где мы ввели понятие стратегической неопределенности. Даже в случаях, когда все правила игры (стратегии, имеющиеся в распоряжении игроков, и выигрыши каждого игрока как функция стратегий всех игроков) известны и не подвержены влиянию внешних факторов неопределенности, таких как погода, каждый игрок может испытывать неопределенность относительно действий, предпринимаемых одновременно с ним другими игроками. Точно так же, если прошлые действия не поддаются наблюдению, каждый игрок может испытывать неопределенность по поводу действий других игроков в прошлом. Как же игрокам делать выбор в условиях такой стратегической неопределенности? Они должны составить субъективное мнение или оценку действий других игроков, что, собственно, и позволяет осуществить концепция убеждения.
А теперь представьте себе равновесие Нэша в таком контексте. Мы определили его как конфигурацию стратегий, при которой стратегия каждого игрока представляет собой лучший ответ на стратегии других игроков. Если игрок не располагает информацией о фактическом выборе остальных участников игры, но имеет о нем определенные убеждения, в равновесии Нэша они должны быть правильными: фактические действия других игроков должны соответствовать вашим убеждениям. Следовательно, мы можем дать альтернативное и эквивалентное определение: равновесие Нэша — это такая совокупность стратегий (по одной на каждого игрока), при которой 1) у каждого игрока есть правильные убеждения о стратегиях других игроков; 2) стратегия каждого игрока — лучшая для него самого с учетом его убеждений относительно стратегий других игроков.
Данный подход к оценке равновесия Нэша имеет два преимущества. Во-первых, концепция лучшего ответа больше не содержит логического противоречия. Каждый игрок выбирает свой лучший ответ не на не поддающиеся наблюдению действия других игроков, а на собственные уже сформировавшиеся убеждения в отношении их действий. Во-вторых, как сказано в , где мы допускаем смешанные стратегии, случайность в стратегии одного игрока можно интерпретировать как неопределенность убеждений других игроков в отношении его действий. В этой главе мы будем параллельно использовать обе интерпретации равновесия Нэша.
На первый взгляд может показаться, что формирование правильных убеждений и вычисление лучших ответов — слишком сложная задача для обычного человека. Мы обсудим некоторые критические замечания такого рода, а также эмпирические и экспериментальные данные о равновесии Нэша в в контексте чистых стратегий и в в контексте смешанных стратегий. А пока просто напомним, что практика — критерий истины. Мы сформулируем и проиллюстрируем концепцию Нэша на примере ее применения и надеемся, что так вы лучше поймете ее достоинства и недостатки, чем в ходе абстрактного обсуждения этой темы.
3. Доминирование
Существует категория игр, в которых одна стратегия неизменно оказывается лучше или хуже другой. В таких случаях применяется один способ, позволяющий упростить поиск равновесия Нэша и его интерпретацию.
Эту концепцию отлично иллюстрирует известная игра под названием «дилемма заключенных». Рассмотрим сюжет, регулярно используемый в телесериале Law and Order («Закон и порядок»). Предположим, мужа и жену арестовали по подозрению в преступном сговоре в целях убийства молодой женщины. Детективы Грин и Лупо размещают их в разных камерах предварительного заключения и допрашивают по отдельности. Реальных улик, связывающих эту пару с убийством, очень мало, хотя есть доказательства того, что они причастны к похищению жертвы. Детективы объясняют каждому подозреваемому, что им обоим грозит тюремное заключение за похищение сроком до 3 лет, даже если ни один из них не признается. Кроме того, мужу и жене по отдельности внушают, что детективам «известны» подробности произошедшего и что один из них участвовал в совершении преступления по принуждению второго. При этом подразумевается, что тюремный срок одного признавшегося будет существенно сокращен, если все подробно изложить на бумаге. (Во многих фильмах такого рода в этот момент на стол обычно кладут стандартный блокнот с отрывными страницами из желтой линованной бумаги и карандаш.) И наконец, супругов убеждают, что, если они оба признают свою вину, можно будет говорить о снижении их тюремных сроков, но не настолько, как в случае, если бы один из них сознался, а другой отрицал свою вину.
В такой ситуации муж и жена — два участника игры с одновременными ходами, в которой каждый игрок должен сделать выбор: сознаваться в убийстве или нет. Оба знают, что в случае отказа признать свою вину каждому из них светит 3 года тюрьмы за причастность к похищению. Подозреваемые также знают, что если один из них сознается, то получит всего 1 год благодаря сотрудничеству с полицией, тогда как другой отправится в тюрьму минимум на 25 лет. Если сознаются оба, у них будет возможность договориться о сокращении тюремного срока до 10 лет для каждого.
Варианты выбора и исходы этой игры представлены в таблице игры на рис. 4.4. Стратегии «признать вину» и «отрицать вину» можно также обозначить как «отказ от сотрудничества» и «сотрудничество», поскольку это отображает роли двух игроков в отношениях между ними. Таким образом, стратегия «отказ от сотрудничества» означает нарушение любой молчаливой договоренности с супругом (супругой), а стратегия «сотрудничество» — совершение действия, которое поможет супругу (супруге), а не сотрудничество с полицейскими.

Рис. 4.4. Дилемма заключенных
Здесь выигрыши — это длительность тюремного заключения в случае каждого исхода игры, поэтому более низкие значения лучше для каждого игрока. Этим данный пример отличается от большинства анализируемых нами игр, в которых более высокий выигрыш — это хорошо, а не плохо. Так что хотим вас предупредить, что больше — не всегда лучше. Когда значения выигрышей отражают рейтинг исходов игры, лучшая альтернатива часто обозначается 1, а последовательно увеличивающиеся числа соответствуют следующим худшим альтернативам. Кроме того, в таблице игры с нулевой суммой, в которой показаны только выигрыши одного игрока, построенные по принципу «чем больше, тем лучше», меньшие числа для другого игрока будут лучше. В представленной здесь дилемме заключенных меньшие числа лучше для обоих игроков. Следовательно, если вам когда-либо придется составлять таблицу выигрышей, где большие числа — это плохо, вы должны четко предупредить об этом читателя, но и сами, если будете читать составленные кем-то примеры, не забывайте о данном нюансе.
Теперь рассмотрим игру с дилеммой заключенных на с точки зрения мужа. Он должен подумать, что предпочтет жена. Предположим, он убежден, что она сознается. Тогда его лучший выбор — тоже сознаться, поскольку так он получит 10 лет тюрьмы вместо 25 лет в случае отрицания вины. А если муж полагает, что жена не признается? Опять же, его лучший выбор — сознаться, так как это гарантирует ему всего год заключения вместо трех, которые бы ему обеспечило отрицание вины. Таким образом, в данной игре стратегия «признать вину» для мужа лучше стратегии «отрицать вину» независимо от его убеждений в отношении выбора жены. Будем говорить, что с точки зрения мужа «признать вину» — это доминирующая стратегия, а «отрицать вину» — доминируемая стратегия. Точно так же мы могли бы сказать, что стратегия «признать вину» доминирует над стратегией «отрицать вину» или что стратегия «отрицать вину» доминируется стратегией «признать вину».
Если то или иное действие явно лучшее для игрока независимо от действий других игроков, есть веские основания полагать, что рациональный игрок выберет именно его. Если то или иное действие явно худшее для игрока независимо от действий других игроков, есть не менее серьезные основания считать, что рациональный игрок будет его избегать. Следовательно, доминирование (когда оно существует) образует убедительную основу для теории решений игр с одновременными ходами.
А. Наличие доминирующих стратегий у обоих игроков
В представленной выше дилемме заключенных доминирование должно привести мужа к выбору стратегии «признать вину». Аналогичная логика применима и к выбору жены. Ее стратегия «признать вину» также доминирует над стратегией «отрицать вину», поэтому жена тоже решит сознаться. Следовательно, сочетание стратегий («признать вину», «признать вину») и есть прогнозируемый исход данной игры. Обратите внимание, что это равновесие Нэша. (На самом деле это единственное равновесие Нэша в данной игре.) Каждый игрок выбирает свою оптимальную стратегию.
В нашей игре лучший выбор каждого игрока не зависит от правильности его убеждений в отношении другого игрока (в этом и есть смысл доминирования), однако каждый игрок приписывает другому такую же рациональность, которую демонстрирует сам, поэтому оба должны быть в состоянии сформировать правильные убеждения. А фактическое действие каждого игрока будет наилучшим ответом на фактическое действие другого игрока. Обратите внимание, что факт доминирования стратегии «признать вину» над стратегией «отрицать вину» в случае обоих игроков совершенно не зависит от того, действительно ли они виновны, как во многих эпизодах телесериала «Закон и порядок», или обвинение против них сфабриковано, как в фильме L.A. Confidential («Секреты Лос-Анджелеса»). Все зависит исключительно от схемы выигрышей, определяемой продолжительностью сроков заключения.
Любая игра со схемой выигрышей как на обозначается общим названием «дилемма заключенных». А если конкретнее, то дилемме заключенных свойственны три ключевые особенности. Во-первых, в распоряжении каждого игрока есть две стратегии: сотрудничать с соперником (в нашем примере — отрицать любую причастностью к преступлению) или нет (признать вину в совершении преступления). Во-вторых, каждый игрок имеет доминирующую стратегию (признать вину или отказаться от сотрудничества). И наконец, равновесие в доминирующих стратегиях хуже для обоих игроков, чем неравновесная ситуация, при которой каждый игрок использует доминируемую стратегию (сотрудничать с соперниками).
Игры такого типа особенно важны при изучении теории игр по двум причинам. Первая — структура выигрышей, присущая дилемме заключенных, присутствует во многих стратегических ситуациях, касающихся экономической, социальной, политической и даже биологической конкуренции. Столь широкий диапазон применения дилеммы заключенных повышает важность ее изучения и понимания со стратегической точки зрения. Этой теме посвящена вся и некоторые разделы других глав.
Вторая — несколько необычный характер равновесного исхода, достигаемого в играх с дилеммой заключенных. Оба игрока выбирают свои доминирующие стратегии, однако полученный равновесный исход обеспечивает им выигрыши ниже, чем они могли бы получить, предпочтя доминируемые стратегии. Следовательно, в дилемме заключенных равновесный исход, по сути, плохой исход для игроков. Существует иной исход, который оба бы предпочли равновесному, но проблема в том, как гарантировать, что никто из игроков не прибегнет к обману. На данной особенности дилеммы заключенных сфокусировались специалисты по теории игр и поставили вполне резонный вопрос: что могут сделать участники игры «дилемма заключенных», чтобы достичь ее лучшего исхода? Мы пока оставим его открытым и продолжим обсуждение игр с одновременными ходами, а затем вернемся к нему и проанализируем более подробно в .
Б. Наличие доминирующей стратегии у одного игрока
Если у рационального игрока есть доминирующая стратегия, он обязательно ее использует, и другой игрок может в этом не сомневаться. В дилемме заключенных это касается обоих игроков, тогда как в ряде других игр — только одного из участников. Если вы играете в игру, не имея доминирующей стратегии в отличие от соперника, можете исходить из предположения, что он применит ее, а значит, у вас есть возможность выбрать свое равновесное действие (наилучший ответ) с учетом данного факта.
Проиллюстрируем этот случай на примере игры между Конгрессом, отвечающим за фискальную политику (налоги и правительственные расходы), и Федеральной резервной системой (ФРС), осуществляющей монетарную политику. В упрощенной версии, в которой представлены только самые важные аспекты такой игры, фискальная политика Конгресса может сводиться либо к сбалансированному бюджету, либо к дефициту бюджета, а ФРС может устанавливать либо высокие, либо низкие процентные ставки. В реальной жизни эту игру нельзя однозначно отнести к числу игр с одновременными ходами, поскольку даже если выбор в ней делается последовательно, не всегда бывает понятно, кто ходил первым. Мы рассмотрим здесь вариант игры с одновременными ходами, а в проанализируем, как будут отличаться исходы при изменении правил игры.
Почти все хотят снижения налогов. При этом немало претендентов на государственное финансирование: оборона, образование, здравоохранение и т. д. Кроме того, существуют различные политически влиятельные группы (в том числе фермеры и отрасли промышленности, страдающие от иностранной конкуренции), нуждающиеся в правительственных субсидиях. Поэтому Конгресс находится под постоянным давлением в плане как снижения налогов, так и увеличения расходов. Однако такой подход становится причиной образования дефицита бюджета, что, в свою очередь, может повлечь за собой рост инфляции. Главная задача ФРС — предотвратить инфляцию. Но ФРС тоже пребывает под политическим прессингом со стороны многих заинтересованных групп, ратующих за снижение процентных ставок, особенно домовладельцев, которым выгодны более низкие ставки по ипотечным кредитам. Снижение процентных ставок приводит к повышению спроса на автомобили, жилье и капиталовложения компаний, но этот спрос может обусловить и рост инфляции. Как правило, ФРС охотно понижает процентные ставки, но только до тех пор, пока нет угрозы инфляции. А она уменьшается, если правительство поддерживает сбалансированность бюджета. С учетом всех этих условий мы построили для этой игры матрицу выигрышей, представленную на рис. 4.5.
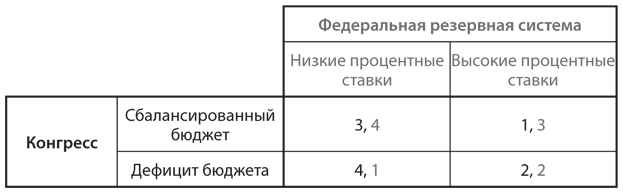
Рис. 4.5. Игра с фискальной и монетарной политикой
Для Конгресса лучший (выигрыш 4) — исход с дефицитом бюджета и низкими процентными ставками, что удовлетворяет всех непосредственных участников политического процесса. Правда, это чревато проблемами в будущем, но в политике временные интервалы непродолжительны. По той же причине худший для Конгресса (выигрыш 1) — исход со сбалансированным бюджетом и высокими процентными ставками. Из двух других исходов Конгресс предпочитает исход со сбалансированным бюджетом и низкими процентными ставками (выигрыш 3): он отвечает интересам домовладельцев как представителей важного среднего класса, а низкие процентные ставки предполагают меньше расходов на обслуживание государственного долга, поэтому в сбалансированном бюджете остается место для многих других статей расходов или снижения налогов.
Для ФРС худший (выигрыш 1) — исход с бюджетным дефицитом и низкими процентными ставками, поскольку это сочетание самое инфляционное; лучший (выигрыш 4) — исход со сбалансированным бюджетом и низкими процентными ставками, потому что это сочетание может выдержать высокий уровень экономической активности без большого риска инфляции. Сопоставив два оставшихся исхода с высокими процентными ставками, ФРС выбирает исход со сбалансированным бюджетом, так как он снижает риск инфляции.
Теперь давайте поищем в этой игре доминирующие стратегии. ФРС добьется более высоких результатов за счет низких процентных ставок, если считает, что Конгресс выберет сбалансированный бюджет (в таком случае выигрыш ФРС составит 4, а не 3). С другой стороны, ФРС выгоднее поднять процентные ставки исходя из убеждения, что Конгресс предпочтет дефицит бюджета (тогда выигрыш ФРС составит 2, а не 1). Таким образом, у ФРС нет доминирующей стратегии, а вот у Конгресса она есть. Если он убежден, что ФРС введет низкие процентные ставки, ему выгоднее выбрать бюджетный дефицит, а не сбалансированный бюджет (при этом выигрыш Конгресса составит 4 вместо 3), как, собственно, и в случае высоких процентных ставок (выигрыш Конгресса составит 2 вместо 1). Следовательно, выбор бюджетного дефицита — доминирующая стратегия Конгресса.
Итак, выбор Конгресса очевиден. Какими бы ни были его убеждения в отношении действий ФРС, он предпочтет дефицит бюджета. ФРС же может учесть этот выбор при принятии своего решения. Федеральная резервная система должна отталкиваться от убеждения, что Конгресс применит свою доминирующую стратегию (дефицит бюджета), и исходя из этого выбрать свою лучшую стратегию, то есть высокие процентные ставки.
При таком исходе игры каждая сторона получает выигрыш 2. Однако внимательное изучение показывает, что, как и в дилемме заключенных, существует еще один исход (а именно сбалансированный бюджет и низкие процентные ставки), способный обеспечить обоим игрокам более высокие выигрыши (3 для Конгресса и 4 для ФРС). Почему же он недостижим в качестве равновесия? Проблема в том, что у Конгресса возникнет искушение отклониться от заявленной стратегии и незаметно создать дефицит бюджета. ФРС, в свою очередь, зная о подобном соблазне и во избежание худшего исхода (выигрыш 1), тоже отклонится от своей стратегии и повысит ставки. В и мы расскажем, как обе стороны могут преодолеть эту трудность, чтобы достичь обоюдовыгодного исхода. Но следует отметить, что в большинстве стран в разные времена эти два политических органа действительно оказывались в тупиковой ситуации, когда фискальная политика была слишком мягкой, а монетарная требовала ужесточения, чтобы сдерживать инфляцию.
В. Последовательное исключение доминируемых стратегий
До сих пор в рассмотренных нами играх в распоряжении каждого игрока было по две чистые стратегии. Если одна стратегия в таких играх доминирующая, а другая — доминируемая, то выбор первой равнозначен исключению второй. В более масштабных играх некоторые стратегии игрока могут быть доминируемыми, даже если при этом ни одна стратегия не доминирует над остальными. Если игроки оказываются в игре данного типа, у них есть шанс добиться равновесия посредством исключения доминируемых стратегий из рассмотрения в качестве возможных вариантов выбора. Такое исключение уменьшает размер игры, а в «новой» игре у того же игрока или у его соперника может быть другая доминируемая стратегия, которую тоже можно удалить. В «новой» игре у одного из участников может даже появиться доминирующая стратегия. Последовательное, или итеративное, исключение доминируемых стратегий сводится к их удалению и сокращению размера игры до тех пор, пока дальнейшее сокращение не станет невозможным. Когда этот процесс завершается уникальным исходом, говорят, что игра разрешима по доминированию. Такой исход представляет собой равновесие Нэша, а стратегии, которые его обеспечивают, — равновесные стратегии каждого игрока.
Давайте возьмем в качестве примера этого процесса игру, представленную на . Рассмотрим первые стратегии Строки. Если какая-то стратегия неизменно обеспечивает этому игроку худшие выигрыши, то она является доминируемой и ее можно исключить из рассмотрения в поисках равновесного выбора Строки. В данном примере единственная доминируемая стратегия Строки — «высоко», над которой доминирует стратегия «внизу»: если Столбец выберет стратегию «слева», Строка получит выигрыш 5 за счет стратегии «внизу» и 4 — за счет стратегии «высоко»; если Столбец предпочтет стратегию «справа», Строка получит выигрыш 9, применив стратегию «внизу», и только 6 в случае «высоко». Следовательно, мы можем исключить стратегию «высоко» из рассмотрения. Теперь проанализируем варианты выбора Столбца на предмет исключения. Стратегия Столбца «слева» доминируется стратегией «справа» (что подтверждают аналогичные рассуждения: 1 < 2, 2 < 3 и 6 < 7). Обратите внимание, что мы не могли сделать такой вывод раньше, до удаления стратегии Строки «высоко»: в игре против стратегии Строки «высоко» Столбец получил бы выигрыш 5 за счет стратегии «слева» и только 4 за счет стратегии «справа». Стало быть, первый этап исключения стратегии Строки «высоко» позволяет перейти ко второму этапу, сводящемуся к удалению стратегии Столбца «слева». Таким образом, в контексте оставшегося набора стратегий («вверху», «низко» и «внизу» у Строки и «посредине» и «справа» у Столбца) стратегии Строки «вверху» и «внизу» доминируемы стратегией «низко». Когда у Строки остается только стратегия «низко», Столбец выберет свой наилучший ответ — а именно стратегию «посредине».
Следовательно, эта игра разрешима по доминированию, а ее исход — «низко»/«посредине» с выигрышами 5, 4. Мы определили его как равновесие Нэша, когда впервые иллюстрировали данную концепцию с помощью этой игры. Теперь более подробно рассмотрели процесс размышлений игроков, приводящий к формированию правильных убеждений. Рациональный игрок Строка не выберет стратегию «высоко». Рациональный игрок Столбец поймет это и, взвесив эффективность своих стратегий против оставшихся у Строки, не выберет «слева». Строка, в свою очередь, предвидя это, не выберет ни «вверху», ни «внизу». И наконец, Столбец, проанализировав все это, применит «посредине».
Другие игры могут быть не разрешимы по доминированию, а последовательное исключение доминируемых стратегий может не обеспечить уникальный исход игры. Но даже в таких случаях исключение доминируемых стратегий позволяет уменьшить размер игры и облегчить ее решение с помощью одного или более методов, описанных в следующих разделах. Стало быть, исключение доминируемых стратегий может стать полезным шагом на пути к решению большой игры с одновременными ходами, даже если не предоставляет возможности решить ее полностью.
До сих пор в процессе анализа итеративного исключения доминируемых стратегий все сравнения выигрышей носили однозначный характер. Но что если выигрыши окажутся равными? Рассмотрим вариант предыдущей игры, показанной на . В этой ее версии стратегии «высоко» (у Строки) и «слева» (у Столбца) также исключаются. На следующем этапе «низко» по-прежнему доминирует над «вверху», а вот доминирование «низко» над «внизу» стало менее очевидным. Эти две стратегии обеспечивают Строке равные выигрыши в борьбе против стратегии Столбца «посредине», хотя стратегия «низко» все же гарантирует Строке более высокий выигрыш по сравнению со стратегией «внизу» при их использовании против стратегии Столбца «справа». Будем говорить, что с точки зрения Строки в данный момент стратегия «низко» слабо доминирует над стратегией «внизу». Напротив, стратегия «низко» строго доминирует над стратегией «вверху», поскольку обеспечивает более высокие выигрыши, чем стратегия «вверху», разыгранная против обеих стратегий Столбца («посредине» и «справа»), анализируемых на данном этапе.
А теперь хотим предупредить вас вот о чем: последовательное исключение слабо доминируемых стратегий может привести к потере некоторых равновесий Нэша. Рассмотрим игру, представленную на рис. 4.6, где мы вводим Ровену как игрока вместо Строки и Колина вместо Столбца. В случае Ровены стратегия «вверх» слабо доминируема стратегией «вниз»; если Колин сыграет «налево», то Ровена получит лучший выигрыш, применив стратегию «вниз», а не «вверх», а если Колин сыграет «направо», то Ровена получит один и тот же выигрыш от обеих своих стратегий. Точно так же для Колина стратегия «направо» слабо доминирует над стратегией «налево». В таком случае разрешимость по доминированию говорит нам, что сочетание стратегий «вниз»/«направо» — равновесие Нэша. Это действительно так, но «вниз»/«налево» и «вверх»/«направо» — тоже равновесия Нэша. Рассмотрим сочетание «вниз»/«налево». Когда Ровена выбирает «вниз», Колин не может улучшить свой выигрыш, переключившись на стратегию «направо», а когда Колин выбирает «налево», лучший ответ Ровены — сыграть «вниз». Аналогичные рассуждения позволяют убедиться, что «вверх»/«направо» — также равновесие Нэша.
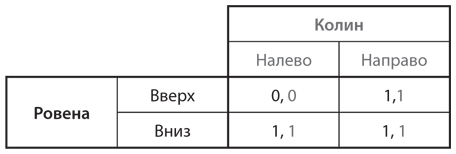
Рис. 4.6. Исключение слабо доминируемых стратегий
В связи с этим при использовании слабого доминирования для исключения некоторых стратегий целесообразно проверить, не пропустили ли вы какие-либо равновесия, с помощью других методов (таких как метод, представленный в следующем разделе). Решение по итеративному доминированию можно считать вероятным равновесием Нэша в этой игре с одновременными ходами, однако следует учитывать также важность множественности равновесий и другие равновесия сами по себе. Мы рассмотрим эти вопросы в следующих главах, проанализировав множественность равновесий в и взаимосвязи между играми с последовательными и одновременными ходами в .
4. Анализ наилучших ответов
Во многих играх с одновременными ходами нет ни доминирующих, ни доминируемых стратегий. Другие игры могут иметь одну или несколько доминируемых стратегий, но их итеративное исключение не обеспечивает единственного исхода игры. В таких случаях необходимо выполнить следующий шаг в процессе поиска решения игры. Мы по-прежнему ищем равновесие Нэша, в котором каждый игрок предпринимает свое лучшее действие с учетом действий другого игрока (игроков), но теперь должны прибегнуть к более тонкому стратегическому мышлению, чем то, которого требует простое исключение доминируемых стратегий.
Здесь мы сформулируем еще один систематический метод поиска равновесий Нэша, который нам очень пригодится при выполнении последующего анализа. Для начала введем требование о правильности убеждений. Мы будем по очереди принимать точку зрения каждого игрока и задавать такой вопрос: какой лучший ответ данного игрока на каждый вариант выбора, который может сделать другой игрок (игроки)? Таким образом мы найдем лучшие ответы каждого игрока на все стратегии, доступные другим игрокам. В математических терминах это означает, что мы найдем стратегию лучшего ответа каждого игрока в зависимости от (или как функцию от) стратегий, находящихся в распоряжении других игроков.
Вернемся к игре, в которую играли Строка и Столбец, и представим ее на рис. 4.7. Сначала проанализируем ответы Строки. Если Столбец применит стратегию «слева», наилучший ответ Строки — «внизу», обеспечивающий выигрыш 5. Мы показываем его, выделив соответствующий выигрыш кружком в таблице игры. Если Столбец предпочтет стратегию «посредине», лучший ответ Строки — «низко» (тоже выигрыш 5). А если Столбец выберет стратегию «справа», оптимальный выбор Строки — снова «низко» (выигрыш 12). Опять же, мы показываем лучшие варианты выбора Строки, обведя кружками соответствующие выигрыши. Аналогичным образом представлены лучшие ответы Столбца, выигрыши по которым выделены кружками: 3 (стратегия «посредине» как лучший ответ на стратегию Строки «вверху»), 5 («слева» как лучший ответ на «высоко»), 4 («посредине» как лучший ответ на «низко») и 7 («справа» как лучший ответ на «внизу»). Мы видим, что в одной ячейке — а именно «низко»/«посредине» — оба выигрыша выделены кружками. Следовательно, стратегии «низко» у Строки и «посредине» у Столбца одновременно будут лучшими ответами друг на друга. Мы нашли равновесие Нэша в этой игре еще раз.
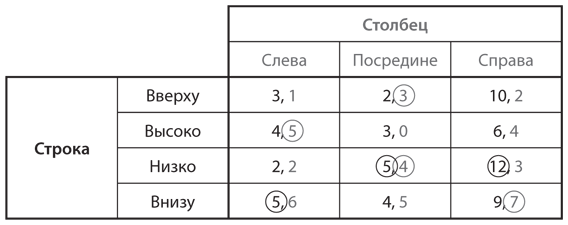
Рис. 4.7. Анализ наилучших ответов
Анализ наилучших ответов — это исчерпывающий способ обнаружения в игре всех возможных равновесий Нэша. Вам следует углубить понимание этого метода, применив его ко всем играм, описанным в данной главе. Примеры с доминированием представляют особый интерес. Если у Строки есть доминирующая стратегия, именно она будет наилучшим ответом на все стратегии Столбца; следовательно, все наилучшие ответы Строки расположены по горизонтали в одной и той же строке. Точно так же, если у Столбца есть доминирующая стратегия, то все его наилучшие ответы выстроятся по вертикали в одном и том же столбце. Вы можете сами проверить, как такой анализ позволяет определить равновесия Нэша в дилемме заключенных с участием мужа и жены, показанной на , и в игре между Конгрессом и Федеральной резервной системой, отображенной на .
В некоторых играх анализ наилучших ответов не позволяет найти равновесие Нэша, подобно тому как разрешимость по доминированию не всегда обеспечивает требуемый результат. Однако в данном случае мы можем сказать кое-что более конкретное, чем при неудачной попытке использовать доминирование. Когда анализ наилучших ответов в игре с дискретными стратегиями не обнаруживает равновесия Нэша, это означает, что в этой игре нет равновесия в чистых стратегиях. Мы рассмотрим игры такого типа в данной главы, а в расширим область применения анализа наилучших ответов на игры, в которых стратегии представляют собой непрерывные переменные, например цены или расходы на рекламу. Кроме того, мы построим кривые наилучших ответов, что позволит нам находить равновесия Нэша, и увидим, что в подобных играх равновесие может отсутствовать с меньшей вероятностью в силу непрерывности выбора стратегий.
5. Три игрока
До сих пор мы анализировали только игры между двумя участниками. Однако все рассмотренные методы анализа применимы и для поиска равновесий Нэша в чистых стратегиях в любой игре с одновременными ходами с участием любого количества игроков. Когда в игре больше двух участников, каждому из которых доступно сравнительно небольшое количество чистых стратегий, анализ можно выполнить с помощью таблицы игры, подобно тому как мы это делали в первых четырех разделах данной главы.
В мы рассматривали игру с тремя участницами, каждая из которых имела по две чистые стратегии. Эмили, Нине и Талии предстояло решить, вносить ли вклад в создание декоративного сада на их маленькой улице. Мы предположили, что в случае вклада всех трех участниц игры сад будет не лучше, чем при вкладе двоих девушек, а вот если вклад сделает только одна участница, сад получится настолько скудным, что уж лучше его и не высаживать вовсе. Теперь допустим, что три участницы делают выбор одновременно, а разнообразие возможных исходов и выигрышей несколько богаче. В частности, размер и пышность сада будут зависеть от точного количества инвесторов: вклад трех участниц позволит разбить самый большой и красивый сад, двух — средний сад и одной — маленький.
Предположим, Эмили анализирует вероятные исходы игры «уличный сад». Ей предстоит оценить шесть возможных вариантов. Эмили может выбирать, вносить или не вносить вклад, если и Нина, и Талия внесут свой вклад или если ни одна из них этого не сделает либо сделает только одна. С точки зрения Эмили, лучший возможный исход с рейтингом 6 — воспользоваться добротой соседок и сделать так, чтобы Нина и Талия инвестировали в создание сада, а она сама — нет. Тогда Эмили могла бы наслаждаться средним садом, не вкладывая в него заработанные тяжелым трудом деньги. Если Нина и Талия вложат средства в сад и Эмили тоже, она сможет любоваться большим прекрасным садом, но ценой собственного вклада, поэтому она присваивает этому исходу рейтинг 5.
На другом конце диапазона находятся исходы, возникающие в случае отказа Нины и Талии инвестировать в сад. При таком раскладе Эмили снова предпочтет не вносить вклад, поскольку иначе все расходы на создание общественного сада, которым будут наслаждаться все, лягут на ее плечи; уж лучше она посадит цветы у себя во дворе. Таким образом, если другие участницы игры отказываются вкладывать средства в создание сада, Эмили присваивает рейтинг 1 исходу, при котором она вносит вклад, и рейтинг 2 исходу, при котором она этого не делает.
Между крайними случаями находятся ситуации, в которых кто-то один — либо Нина, либо Талия — вносит вклад, но не сразу обе. Когда одна из них это делает, Эмили знает, что сможет наслаждаться маленьким садом, не принимая участия в его создании. Кроме того, она считает, что цена ее вклада перевешивает то, что он позволит увеличить размер сада. Поэтому Эмили присваивает рейтинг 4 исходу, при котором она не вносит вклад, но получает возможность наслаждаться маленьким садом, и рейтинг 3 исходу, при котором вносит вклад, обеспечивая создание среднего сада. Поскольку Нина и Талия придерживаются аналогичных взглядов на затраты и преимущества, каждая из них составляет такой же рейтинг вероятных исходов игры, в котором самый худший — когда каждая участница инвестирует в создание сада, а две оставшиеся этого не делают, и т. д.
Если все трое решают, вносить ли вклад в создание сада, не зная о действиях соседок, перед нами — игра с одновременными ходами с тремя игроками. Для того чтобы найти в ней равновесие Нэша, необходимо составить таблицу игры. В случае игры с тремя участниками таблица должна быть трехмерной, а стратегии третьего игрока должны соответствовать третьему измерению. Самый простой способ его прибавить к двумерной таблице игры — добавить страницы. Первая страница таблицы отображает выигрыши для первой стратегии третьего игрока, вторая страница — выигрыши для второй стратегии третьего игрока и т. д.
Мы показываем трехмерную таблицу игры «уличный сад» на рис. 4.8. В ней две строки отведены для двух стратегий Эмили, два столбца — для двух стратегий Нины и две страницы — для двух стратегий Талии. Мы разместили эти страницы рядом, чтобы вы могли видеть все одновременно. В каждой ячейке выигрыши перечислены в следующем порядке: сначала выигрыш игрока строки, затем выигрыш игрока столбца, далее выигрыш игрока страницы, то есть в данном примере: Эмили, Нина, Талия.
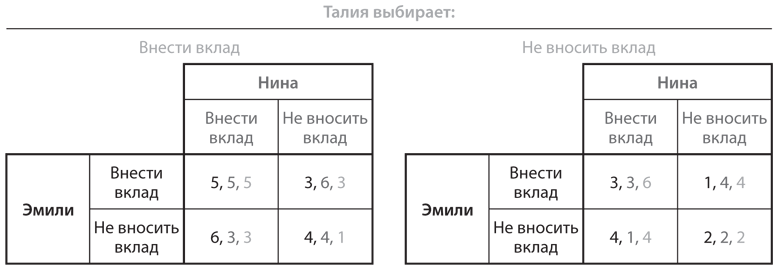
Рис. 4.8. Игра «уличный сад»
Прежде всего мы должны определить, есть ли доминирующие стратегии у каждой из участниц. В таблицах игр из одной страницы это было достаточно просто: мы просто сравнивали исходы, связанные с одной из стратегий игрока, с исходами другой его стратегии. На практике в случае игрока строки такое сравнение требовало простой проверки данных в столбцах одной страницы таблицы и наоборот в случае игрока столбца. Сейчас же мы должны проверить данные на обеих страницах таблицы, чтобы определить, есть ли доминирующая стратегия у какой-либо из участниц игры.
В случае Эмили мы сравниваем две строки обеих страниц таблицы и видим, что если Талия внесет вклад, то доминирующая стратегия Эмили — не вносить вклад. Следовательно, для Эмили лучше не вносить вклад в создание сада независимо от решений остальных участниц игры. Точно так же мы видим, что доминирующая стратегия Нины (на обеих страницах таблицы) — не вносить вклад. А вот при поиске доминирующей стратегии у Талии нужно быть предельно внимательными. Мы должны сравнить исходы, которые поддерживают постоянство поведения Эмили и Нины, проанализировав выигрыши Талии в случае выбора стратегии «внести вклад» в сравнении с выигрышами от выбора стратегии «не вносить вклад». Иными словами, мы должны сравнить ячейки двух страниц таблицы: верхнюю левую ячейку первой страницы (слева) с верхней левой ячейкой второй страницы (справа) и т. д. Как и для первых двух участниц игры, этот процесс показывает, что доминирующая стратегия Талии — тоже не вносить вклад.
Итак, у каждой участницы игры есть доминирующая стратегия, которая должна быть ее равновесной чистой стратегией. Равновесие Нэша в этой игре состоит в том, что все ее участницы предпочитают не вкладывать средства в создание сада и получить второй по величине выигрыш. При этом сад так и не будет посажен, а участницы игры не понесут лишних расходов.
Обратите внимание, что эта игра — еще один пример дилеммы заключенных. Существует единственное равновесие Нэша, при котором все игроки получают выигрыш 2. Однако у «уличного сада» есть еще один исход (при котором все три соседки инвестируют в сад), обеспечивающий всем трем участницам более высокие выигрыши 5. Хотя каждой из них было бы выгодно поучаствовать в создании сада, ни у кого из них нет индивидуального стимула для этого. В итоге такие сады либо вообще не сажают, либо делают это за счет налоговых поступлений, поскольку городская администрация может взыскать с жителей города такой налог. В мы рассмотрим другие дилеммы коллективного действия и изучим некоторые методы их решения.
Равновесие Нэша в игре «уличный сад» можно также найти посредством анализа наилучших ответов, как показано на рис. 4.9. Так как доминирующая стратегия каждой участницы игры — «не вносить вклад», все наилучшие ответы Эмили находятся в ее строке «не вносить вклад», Нины — в ее колонке «не вносить вклад», а Талии — на ее странице «не вносить вклад». Ячейка в правом нижнем углу содержит три наилучших ответа, а значит, это и есть равновесие Нэша.
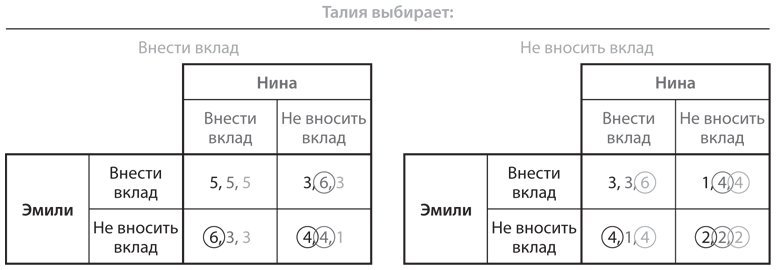
Рис. 4.9. Анализ наилучших ответов в игре «уличный сад»
6. Множество равновесий в чистых стратегиях
В каждой из игр, рассмотренных в предыдущих разделах, было единственное равновесие Нэша в чистых стратегиях. Однако в целом в играх необязательно должно быть единственное равновесие Нэша. Мы проиллюстрируем этот результат посредством класса игр, имеющих много областей применения, который можно обозначить как координационные игры. У их участников есть общие интересы (хотя и не всегда полностью совпадающие), но поскольку игроки действуют независимо друг от друга (в силу характера некооперативных игр), координация действий, необходимых для достижения общего предпочтительного исхода, проблематична.
А. Встретятся ли Гарри и Салли? Чистая координация
Для того чтобы проиллюстрировать эту идею, давайте представим себе двух студентов-старшекурсников, встретившихся в университетской библиотеке. Они понравились друг другу и хотели бы продолжить общение, но им нужно идти в разные аудитории на лекции. Гарри и Салли договариваются вместе выпить кофе после занятий, которые заканчиваются в 16:30. Во время лекций оба осознают, что из-за волнения забыли договориться о месте встречи. Существует два возможных варианта: Starbucks и Local Latte. К сожалению, эти кафе расположены на противоположных концах большого кампуса, поэтому оказаться в обоих примерно в одно и то же время невозможно. Кроме того, Гарри и Салли не обменялись телефонными номерами, из-за чего не могут отправить друг другу сообщения. Что же нужно сделать каждому из них?
На рис. 4.10 эта ситуация представлена в виде игры с матрицей выигрышей. У каждого игрока два варианта выбора: Starbucks и Local Latte. Выигрыш для каждого равен 1, если они встретятся, и 0, если нет. Анализ наилучших ответов позволяет быстро определить, что в игре два равновесия Нэша: одно — при котором Салли и Гарри выберут Starbucks, и второе — при котором они выберут Local Latte. Для обоих важно достичь одного из этих равновесий, причем какого — не играет роли, поскольку оба равновесия обеспечивают одинаковые выигрыши. Главное, чтобы они скоординированно выбрали одно и то же действие, неважно какое. Именно поэтому такую игру называют игрой с чистой координацией.
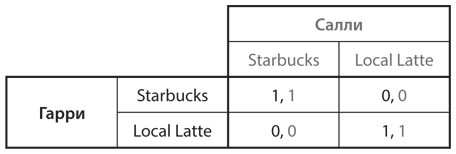
Рис. 4.10. Чистая координация
Но смогут ли Гарри и Салли успешно скоординировать свои действия? Или в конечном счете они окажутся в разных кафе и каждый будет думать, что другой его подвел? Увы, такой риск существует. Гарри может решить, что Салли отправится в Starbucks, потому что она что-то говорила о занятиях, которые проходят на той стороне кампуса, где расположен Starbucks. Но у Салли может быть противоположное убеждение относительно того, что сделает Гарри. При наличии множества равновесий Нэша игрокам при выборе одного из них необходим какой-то способ скоординировать свои убеждения или ожидания в отношении действий друг друга.
Эта ситуация аналогична тому, что произошло с героями истории «Какая шина?», рассказанной в , где мы обозначили метод координации термином «фокальная точка». В данном контексте одно из двух кафе может быть широко известно как место встречи студентов. Однако недостаточно, чтобы Гарри просто об этом знал. Он должен знать, что Салли знает, и что она знает, что он знает, и т. д. Иными словами, их ожидания должны сходиться в фокальной точке. В противном случае Гарри может сомневаться в том, куда пойдет Салли, поскольку он не знает, что она думает о том, куда пойдет он. Подобные сомнения могут возникнуть на третьем, или четвертом, или еще более высоком уровне размышлений о размышлениях.
Когда один из нас (Диксит) задал этот вопрос своим студентам, большинство первокурсников выбрали Starbucks, а старшекурсники — местное кафе в студенческом центре университетского городка. Такой расклад закономерен: первокурсники, которые прожили в кампусе совсем немного времени, фокусируют свои ожидания на всем известной национальной сети кафе, тогда как старшекурсники знают местное кафе, ставшее для них самым лучшим местом встречи, и считают, что их друзья придерживаются аналогичного мнения.
Если бы одно кафе было оформлено в оранжевых тонах, а другое — в багровых, то в Принстоне первое кафе служило бы в качестве фокальной точки, поскольку оранжевый — это цвет Принстонского университета, тогда как в Гарварде по той же причине фокальной точкой было бы кафе с багровым декором. Если один человек — студент Принстона, а другой — Гарварда, они могут вообще не встретиться: либо потому, что каждый из них считает свой цвет более приоритетным, либо по той причине, что каждый думает, что другой не проявит гибкость и не пойдет на компромисс. В более общем случае способность участников координационных игр найти фокальную точку зависит от наличия такой общеизвестной точки контакта, будь то историческая, культурная или языковая.
Б. Встретятся ли Гарри и Салли? И где? Игра в доверие
Теперь давайте немного изменим выигрыши в игре. Поведение студентов старших курсов позволяет предположить, что нашей паре может быть не совсем безразлично, какое именно кафе выбирать. В одном заведении может быть лучше кофе, в другом — атмосфера. Или они могут предпочесть менее популярное место встречи студентов, чтобы избежать возможного столкновения с бывшими парнями или девушками. Предположим, Гарри и Салли остановятся на Local Latte; следовательно, выигрыш каждого из них составит 2, если они встретятся в этом кафе, и 1, если они встретятся в Starbucks. Новая матрица выигрышей показана на рис. 4.11.
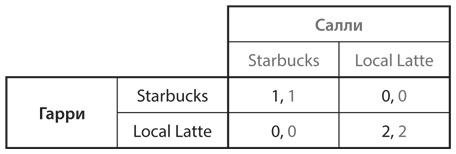
Рис. 4.11. Игра в доверие
Здесь снова присутствуют два равновесия Нэша. Однако в данной версии игры каждый предпочитает равновесие, при котором оба выбирают Local Latte. К сожалению, тот факт, что обоим участникам нравится такой исход игры, его не гарантирует. Прежде всего (как и всегда в нашем анализе) выигрыши должны быть элементом общего знания, оба игрока должны знать всю матрицу выигрышей, оба должны знать, что оба знают, и т. д. Знание игры во всех подробностях было бы возможным, если бы Гарри и Салли обсудили ситуацию и сошлись во мнениях по поводу преимуществ двух кафе, но просто забыли договориться о том, что встретятся в Local Latte. Но даже в этом случае Гарри мог бы подумать, что у Салли есть какая-то иная причина для выбора Starbucks, или он может подумать, что она подумает, что он подумает, и т. д. Без истинной сходимости ожиданий в отношении действий участники игры могут выбрать худшее равновесие или, что еще печальнее, вообще не скоординировать свои действия, и тогда каждый получит нулевой выигрыш.
Повторим еще раз: участники игры, представленной на , могут получить предпочтительный равновесный исход, только если каждый из них достаточно убежден в том, что другой выберет надлежащее действие. По этой причине игры такого типа называются играми в доверие.
Во многих подобных реальных жизненных ситуациях обрести доверие довольно легко при наличии даже минимальной коммуникации между игроками. Их интересы полностью совпадают: если один скажет «Я пойду в Local Latte», у другого нет оснований сомневаться в истинности этого утверждения, поэтому он пойдет туда же, чтобы получить предпочтительный для обоих исход. Именно поэтому нам пришлось придумать историю с двумя студентами, которые посещают разные занятия и не имеют возможности общаться друг с другом. Если интересы игроков вступают в конфликт, правдивая коммуникация становится более проблематичной. Мы углубимся в эту проблему, когда будем рассматривать стратегическое манипулирование информацией в играх в .
В более многочисленных группах коммуникацию можно обеспечить посредством планирования встреч или размещения объявлений. Но эти способы эффективны только в случае, когда все знают, что остальные обращают на них внимание, поскольку для успешной координации действий необходимо, чтобы требуемый исход был фокальной точкой. Ожидания игроков должны сходиться в этой точке: все должны знать, что каждый знает, что … каждый делает этот выбор. Именно эту функцию выполняют многие общественные институты и договоренности. Собрания, во время которых присутствующие рассаживаются по кругу и смотрят в его центр, позволяют каждому видеть, что делают остальные. Рекламные объявления во время Суперкубка, особенно когда их показывают накануне матчей в качестве основной приманки, убеждают каждого зрителя, что многие тоже их смотрят. Это делает такие рекламные объявления особенно привлекательными для компаний, выпускающих продукты, которые становятся более желанными для каждого отдельного покупателя, если их покупают многие люди; к данной категории относится продукция компьютерной отрасли, телекоммуникаций и интернет-индустрии.
В. Встретятся ли Гарри и Салли? И где? Битва полов
Теперь давайте еще немного усложним игру с выбором кафе. Оба игрока хотят встретиться, но предпочитают разные кафе. Таким образом, Гарри может получить выигрыш 2, а Салли — 1, если они встретятся в Starbucks, и наоборот, если встреча состоится в Local Latte. Матрица выигрышей этой игры показана на рис. 4.12.
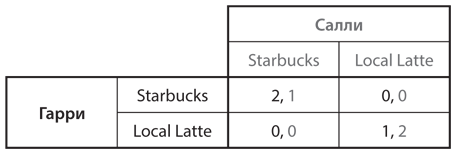
Рис. 4.12. Битва полов
Такая игра называется битвой полов. Название происходит от истории, которую специалисты по теории игр придумали для иллюстрации этой структуры выигрышей в сексистских 1950-х годах. В этой истории мужу и жене предстоял выбор между походом на боксерский матч и балет, причем (предположительно, по эволюционно-генетическим причинам) муж должен был выбрать бокс, а жена — балет. Это название прижилось, поэтому мы будем его использовать, хотя наш пример (в котором у любого из игроков вполне могла быть причина предпочесть любое из двух кафе, не имеющая отношения к полу) ясно дает понять, что такая игра необязательно должна иметь сексистский подтекст.
Как будут развиваться события в этой игре? В ней по-прежнему присутствуют два равновесия Нэша. Если Гарри убежден, что Салли выберет Starbucks, ему лучше сделать то же самое, и наоборот. По тем же причинам Local Latte также является равновесием Нэша. Для того чтобы достичь любого из этих равновесий и избежать исходов, при которых игроки отправятся в разные кафе, им необходима фокальная точка, или сходимость ожиданий, точно так же как в игре с чистыми стратегиями и игре в доверие. Однако в битве полов риск неудачи с координацией действий выше. Игроки с самого начала находятся в достаточно симметричных ситуациях, однако каждое из двух равновесий Нэша обеспечивает им асимметричные выигрыши, а их предпочтения в отношении двух возможных исходов вступают в противоречие: Гарри ратует за встречу в Starbucks, а Салли — в Local Latte. Они должны найти способ нарушить эту симметрию.
В стремлении достичь предпочтительного для себя равновесия каждый игрок может прибегнуть к жестким действиям и стратегии, ведущей к лучшему равновесию. В мы рассмотрим в деталях такие инструменты ведения игры, как стратегические ходы, которые участники подобных игр могут предпринять для обеспечения предпочтительного исхода. Или каждый игрок попытается угодить другому, что может обусловить досадную ситуацию, когда Гарри отправится в Local Latte, чтобы порадовать Салли, но обнаружит, что она решила доставить удовольствие ему и пошла в Starbucks (очень похоже на то, как герои рассказа О’Генри «Дары волхвов» выбирали подарки друг другу на Рождество). В качестве альтернативы в случае повторяющейся игры успешная координация действий может стать предметом переговоров и поддерживаться как равновесие. Например, Гарри и Салли могут договориться встречаться то в одном, то в другом кафе. В мы проанализируем такое неявное сотрудничество в повторяющихся играх в контексте дилеммы заключенных.
Г. Встретятся ли Джеймс и Дин? Игра в труса
Наш последний пример в этом разделе касается координационной игры несколько иного типа. В ней игроки стремятся предотвратить (или не выбирать) одни и те же действия. Кроме того, последствия неудачной попытки координации в подобных играх куда более разрушительны, чем в других играх.
Эта история взята из игры, в которую якобы играли американские подростки в 1950-х годах. Двое подростков садятся в полночь в свои автомобили на противоположных концах улицы какого-нибудь американского городка и мчатся навстречу друг другу. Тот, кто свернет в сторону, чтобы избежать столкновения, становится «трусом», а тот, кто продолжает ехать прямо, считается победителем. Если оба подростка придерживаются прямого курса, происходит столкновение, в котором оба автомобиля получают повреждения, а оба водителя — травмы.
Выигрыши «труса» зависят от того, насколько негативным для себя игрок считает «плохой» исход (в данном случае это травмы водителя и повреждения автомобиля) по сравнению с перспективой прослыть трусом. Если слова задевают меньше, чем хруст металла, то таблица разумных выигрышей в варианте игры в труса 1950-х годов выглядит так, как на рис. 4.13. Каждый игрок больше всего хочет стать победителем, а не трусом, и оба одинаково не хотят столкновения автомобилей. Между этими двумя крайностями для вас предпочтительна ситуация, чтобы ваш соперник оказался трусом в игре с вами (сохранить лицо), чем самому стать трусом.
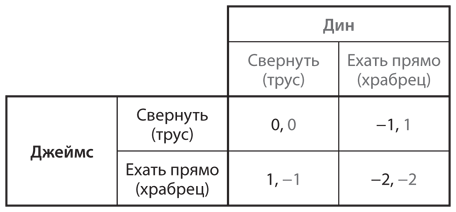
Рис. 4.13. Игра в труса
У этой истории есть четыре важных свойства, которые определяют игру в труса. Во-первых, у каждого игрока есть одна «жесткая» и одна «слабая» стратегия. Во-вторых, в игре присутствуют два равновесия Нэша в чистых стратегиях (иными словами, исходы игры, при которых один из игроков становится трусом или придерживается слабой стратегии). В-третьих, каждый игрок выбирает именно то равновесие, при котором другой игрок предпочитает стать трусом или применяет слабую стратегию. В-четвертых, когда оба придерживаются жесткой стратегии, оба получают очень плохие выигрыши. В играх такого типа реальная игра сводится к проверке ее участниками способов достижения предпочтительного для себя равновесия.
Мы вернулись к ситуации, подобной рассмотренной при обсуждении игры «битва полов». Большинство происходящих в реальной жизни игр в труса предполагают еще более ожесточенные битвы, чем битва полов: преимущества от победы повышаются, так же как и цена поражения, поэтому все проблемы, связанные с конфликтом интересов и асимметрией между игроками, усугубляются. Каждый игрок стремится повлиять на исход такой игры. Может сложиться ситуация, когда один игрок попытается создать впечатление жесткости, которое видели бы все, чтобы запугать соперников. Еще один вариант — найти какой-либо другой способ убедить соперника в том, что вы не сдадитесь, взяв на себя явное и непреложное обязательство ехать прямо. (В мы поговорим о том, как делать ходы с обязательствами.) Кроме того, оба игрока могут захотеть предотвратить неблагоприятный исход (столкновение), если это вообще возможно.
Как и в битве полов, если игра повторяется, молчаливая координация — лучший путь к решению игры. Иначе говоря, если бы подростки играли в труса в полночь каждого воскресенья, при выборе равновесных стратегий они знали бы, что у игры есть и прошлое, и будущее. В подобной ситуации они могли бы выбрать такой логически правильный путь, как чередование равновесий, и по очереди бы становились победителями раз в две недели. (Однако если кто-то узнает об этой сделке, пострадает репутация обоих игроков.)
Существует еще один, последний, момент, касающийся координационных игр, о котором следует упомянуть. Концепция равновесия Нэша требует от каждого игрока наличия правильных убеждений в отношении выбора стратегии другим игроком. При поиске равновесий Нэша в чистых стратегиях эта концепция предписывает, чтобы каждый игрок был уверен в выборе другого игрока. Но наш анализ координационных игр показывает, что в размышлениях о выборе других игроков в таких играх присутствует элемент стратегической неопределенности. Как мы можем включить ее в анализ? В мы вводим понятие смешанной стратегии, в которой фактический выбор делается случайным образом из доступных действий. Такой подход распространяет концепцию равновесия Нэша на ситуации, когда игроки могут быть не уверены в действиях друг друга.
7. Отсутствие равновесия в чистых стратегиях
В каждой из рассмотренных выше игр было минимум одно равновесие Нэша в чистых стратегиях. В некоторых играх, таких как в , было больше одного равновесия, тогда как в предыдущих разделах представлены игры ровно с одним. К сожалению, не все игры, анализируемые нами в процессе изучения стратегии и теории игр, будут иметь легко поддающиеся определению исходы, при которых игроки всегда выбирают одно конкретное действие в качестве равновесной стратегии. В данном разделе мы проанализируем игры, в которых отсутствует равновесие Нэша в чистых стратегиях и ни один из игроков не выбирает неизменно одну и ту же стратегию в качестве своего равновесного действия.
Простой пример такой игры — розыгрыш одного очка в теннисном матче. Представьте себе матч между двумя лучшими теннисистками всех времен — Мартиной Навратиловой и Крис Эверт. Навратилова у сетки только что отправила мяч в сторону Эверт на задней линии, а Эверт вот-вот сделает обводящий удар. Она может попытаться послать мяч либо по линии (ПЛ, сильный прямой удар), либо по диагонали (ПД, более мягкий удар из одного угла корта в другой). Навратилова точно так же должна подготовиться, чтобы прикрыть какую-то одну сторону. Каждая участница игры знает, что не должна давать сопернице никаких подсказок в отношении запланированного действия, понимая, что эта информация будет использована против нее. Навратилова попыталась бы прикрыть ту сторону, в которую Эверт планирует послать мяч, а Эверт сделала бы удар в ту сторону, которую Навратилова не собирается прикрывать. Обе теннисистки должны выполнить соответствующее действие за долю секунды, и обе умеют хорошо скрывать свои намерения до последнего момента. Следовательно, их действия фактически одновременны, поэтому мы можем проанализировать этот розыгрыш очка как игру с одновременными ходами с двумя участниками.
Выигрыши в игре с розыгрышем очков в теннисе соответствуют относительному количеству случаев, когда игрок выигрывает очко в той или иной комбинации обводящего удара и прикрывающей игры. Учитывая, что обводящий удар по линии сильнее удара по диагонали и что Эверт с большей вероятностью выиграет, если Навратилова попытается прикрыть не ту сторону корта, мы можем сформировать приемлемую систему выигрышей. Предположим, Эверт добьется успеха в 80% обводящих ударов по линии, если Навратилова прикроет корт на случай удара по диагонали, и только в 50% обводящих ударов по линии, если Навратилова прикроет корт на случай удара по линии. Точно так же Эверт добьется успеха в 90% ударов по диагонали, если Навратилова прикроет корт на случай удара по линии. Эта доля результативных ударов выше, чем при попытке Навратиловой прикрыть корт на случай удара по диагонали — тогда Эверт выиграет очки только в 20% случаев.
Очевидно, что доля побед Навратиловой в игре равна разности между 100% и долей побед Эверт. Следовательно, это игра с нулевой суммой (хотя формально сумма выигрышей двух участниц составляет 100), поэтому мы можем представить всю необходимую информацию в таблице выигрышей, отобразив в каждой ячейке только выигрыш Эверт. На рис. 4.14 показана таблица выигрышей и доля побед Эверт в розыгрышах очков против Навратиловой в каждой из четырех возможных комбинаций их выбора стратегий.
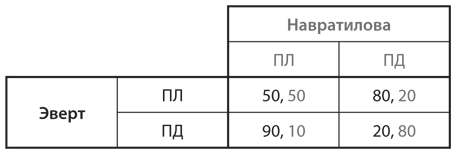
Рис. 4.14. Отсутствие равновесия в чистых стратегиях
Правила решения игр с одновременными ходами говорят нам о том, что сначала следует попытаться найти доминирующие или доминируемые стратегии, а затем использовать анализ наилучшего ответа для поиска равновесия Нэша. Это полезное упражнение позволяет убедиться, что в данной игре нет доминирующих стратегий. Выполнив анализ наилучших ответов, мы приходим к выводу, что лучший ответ Эверт на стратегию ПЛ — стратегия ПД, а на стратегию ПД — стратегия ПЛ. Напротив, наилучший ответ Навратиловой на стратегию ПЛ — стратегия ПЛ, а на стратегию ПД — стратегия ПД. Ни в одной ячейке таблицы выигрышей равновесия Нэша нет, поскольку каждая теннисистка упорно пытается изменить свою стратегию. Например, начав с верхней левой ячейки таблицы, мы обнаружим, что Эверт предпочитает перейти от стратегии ПЛ к стратегии ПД, увеличив свой выигрыш с 50 до 90 процентов. Однако в левой нижней ячейке таблицы мы видим, что Навратилова считает разумным переключиться со стратегии ПЛ на ПД, увеличив свой выигрыш с 10 до 80 процентов. Как вы можете убедиться сами, аналогичным образом Эверт стремится изменить стратегии в нижней левой ячейке, а Навратилова — в верхней правой. В каждой ячейке таблицы одна участница неизменно старается изменить игру, поэтому мы можем бесконечно перемещаться в таблице по кругу в поисках равновесия.
Отсутствие равновесия Нэша в этой и других подобных играх содержит один значимый сигнал: в играх такого типа важно не то, что игроки должны сделать, а то, чего они не должны делать. В частности, каждая участница игры не должна постоянно или систематически выбирать один и тот же удар, оказываясь в такой ситуации. Если любая из теннисисток будет придерживаться определенной линии поведения, другая может воспользоваться этим. (Например, если бы Эверт постоянно делала обводящий удар по диагонали, Навратилова бы знала, что ей каждый раз необходимо прикрывать соответствующую сторону корта, и тем самым снизила бы шансы Эверт на успешное выполнение удара по диагонали.) Самое разумное, что могут сделать участницы игры, — действовать несколько бессистемно, рассчитывая на то, что элемент неожиданности поможет победить соперницу. Асимметричный подход подразумевает выбор каждой стратегии в определенном количестве случаев. (Эверт следует использовать свой более слабый удар достаточно часто, чтобы Навратилова не могла предугадать, какой удар будет направлен в ее сторону. Однако она не должна использовать удары двух типов по установленной схеме, поскольку это также приведет к потере элемента неожиданности.) Подход, при котором игроки выбирают действия случайным образом, известный как смешивание стратегий, подробно рассматривается в . Игра, представленная на , может не иметь равновесия в чистых стратегиях, но ее все же можно решить посредством поиска равновесия в смешанных стратегиях, что мы и сделаем в .
Резюме
Участники игр с одновременными ходами выбирают стратегии, не зная о выборе других игроков. Такие игры можно изобразить в виде таблицы игры, в ячейках которой отображены выигрыши каждого игрока, а ее размерность равна количеству игроков. Игры с нулевой суммой с двумя участниками можно представить в сокращенном виде, отобразив в каждой ячейке таблицы игры только выигрыши одного игрока.
Равновесие Нэша — концепция, используемая для решения игр с одновременными ходами. Такое равновесие состоит из совокупности стратегий (по одной на каждого игрока), где каждый игрок выбрал свой лучший ответ на выбор другого игрока. Кроме того, равновесие Нэша можно трактовать как набор стратегий, при котором у каждого игрока есть правильные убеждения относительно стратегий других игроков, а определенные стратегии являются лучшими для каждого игрока с учетом этих убеждений. Равновесия Нэша можно найти посредством поиска доминирующих стратегий, последовательного исключения доминируемых стратегий или анализа наилучших ответов.
Существует масса классов игр с одновременными ходами. Игра «дилемма заключенных» встречается во многих контекстах. В координационных играх, таких как игра в доверие, игра в труса и битва полов, — множество равновесий, и решение этих игр требует от их участников координации действий. Если в игре отсутствует равновесие в чистых стратегиях, мы должны искать его в смешанных стратегиях, анализ которых представлен в .
Ключевые термины
Анализ наилучших ответов
Битва полов
Дилемма заключенных
Доминируемая стратегия
Доминирующая стратегия
Игра в доверие
Игра в труса
Игра с чистой координацией
Итеративное исключение доминируемых стратегий
Координационная игра
Матрица игры
Наилучший ответ
Нормальная форма
Последовательное исключение доминируемых стратегий
Равновесие Нэша
Разрешимость по доминированию
Смешанная стратегия
Стратегическая форма
Сходимость ожиданий
Таблица выигрыша
Таблица игры
Убеждение
Фокальная точка
Чистая стратегия
Упражнения с решениями
S1. Найдите все равновесия Нэша в чистых стратегиях для представленных ниже игр. Сначала проверьте таблицу игры на наличие доминирующих стратегий. Если таковых нет, решите игру посредством итеративного исключения доминируемых стратегий. Объясните логику своих рассуждений.
a)
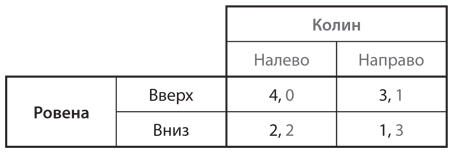
b)
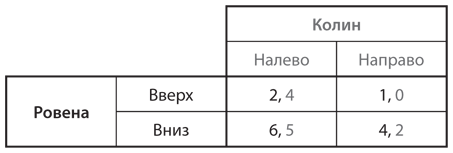
c)
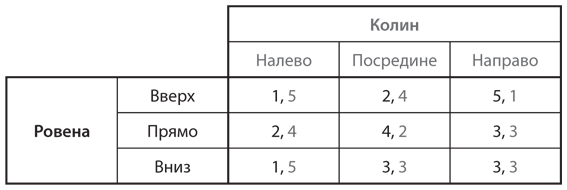
d)
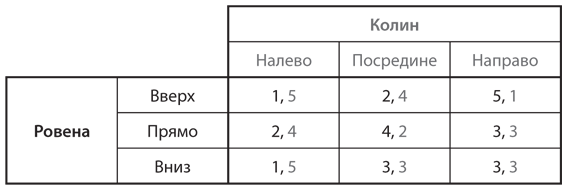
S2. Для каждой из четырех игр, представленных в упражнении S1, определите, это игра с нулевой или с ненулевой суммой. Объясните логику своих рассуждений.
S3. Метод минимакса — еще один значимый способ решения игр с нулевой суммой, разработанный задолго до того, как Нэш сформулировал концепцию равновесия в играх с ненулевой суммой. Для того чтобы его применить, необходимо исходить из предположения, что независимо от того, какую стратегию выберет игрок, его соперник сделает такой выбор, который обеспечит этому игроку худший выигрыш от данной стратегии. В случае каждой игры с нулевой суммой, найденной в упражнении S2, используйте метод минимакса для поиска равновесных стратегий игры, выполнив следующие действия:
a) Для каждой стратегии, соответствующей строке таблицы, запишите минимальный выигрыш Ровены (худшее, что может с ней сделать Колин в данном случае). Для каждой стратегии, отображенной в столбце таблицы, запишите минимальный выигрыш Колина (худшее, что может с ним сделать Ровена в данном случае).
b) Для каждого игрока определите стратегию (или стратегии), которая обеспечивает ему лучший из этих худших выигрышей. Это и есть стратегия минимакса каждого игрока.
(Поскольку в данном случае речь идет об игре с нулевой суммой, наилучшие ответы игроков действительно подразумевают сведение выигрышей друг друга к минимуму, а значит, эти стратегии минимакса и есть равновесиями Нэша. Джон фон Нейман доказал существование минимаксного равновесия в играх с нулевой суммой в 1928 году, за двадцать лет до того, как Нэш обобщил эту теорию.)
S4. Найдите все равновесия Нэша в чистых стратегиях в следующих играх с ненулевой суммой. Опишите шаги, которые вы при этом предприняли.
a)
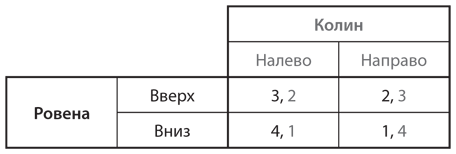
b)
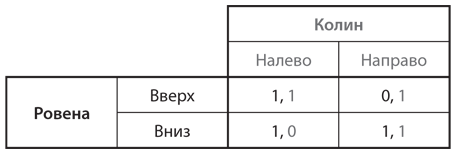
c)
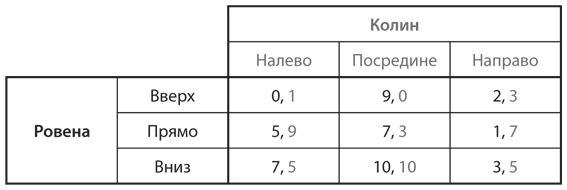
d)
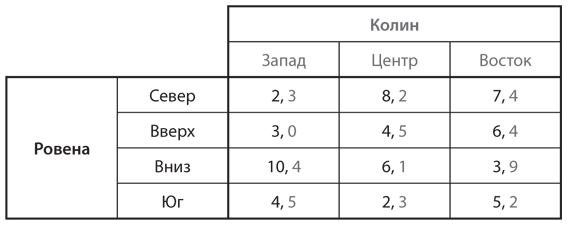
S5. Проанализируйте следующую таблицу игры:
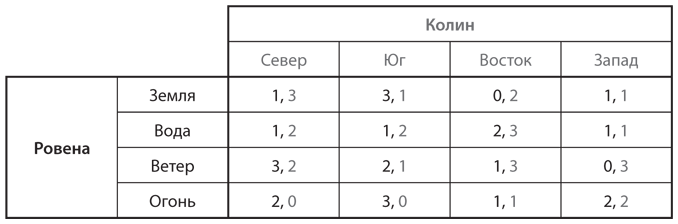
a) Есть ли доминирующая стратегия у Ровены либо у Колина? Объясните, почему есть или нет.
b) Используйте метод итеративного исключения доминируемых стратегий, чтобы как можно больше уменьшить игру. Опишите порядок выполнения такого исключения стратегий и представьте урезанную форму игры.
c) Разрешима ли эта игра по доминированию? Объясните, почему да или нет.
d) Найдите в ней равновесие (или равновесия) Нэша.
S6. «Если у игрока есть доминирующая стратегия в игре с одновременными ходами, значит, он наверняка получит самый лучший исход». Это утверждение истинно или ложно? Обоснуйте свой вывод и приведите пример игры, иллюстрирующий ваш ответ.
S7. Пожилой даме нужна помощь, чтобы перейти улицу. Для этого достаточно одного человека; не имеет смысла привлекать больше людей. Мы с вами находимся поблизости и можем помочь, причем одновременно должны решить, стоит ли это делать. Каждый из нас получит удовольствие с выигрышем 3 единицы, если все разрешится благополучно (независимо от того, кто ее переведет). Однако именно тому, кто непосредственно поможет даме, это обойдется в 1 единицу — такова ценность нашего времени, потраченного на оказание помощи. Если никто из игроков не оказывает помощь, выигрыш каждого будет равен нулю. Сформулируйте эту ситуацию в виде игры. Составьте таблицу выигрышей и найдите равновесия Нэша в чистых стратегиях.
S8. В университете решают, что построить — новую лабораторию или новый театр в кампусе. Факультет естественных наук предпочел бы новую лабораторию, а гуманитарных ратует за театр. Однако финансирование проекта (вне зависимости от того, каким он будет) возможно только в случае единодушной поддержки всего преподавательского состава университета. При возникновении разногласий ни один проект не получит дальнейшего продвижения и оба факультета останутся без нового здания и с наихудшим выигрышем. Собрания двух отдельных групп преподавателей, на которых решается вопрос о поддержке проекта, проходят одновременно, а выигрыши представлены в следующей таблице:
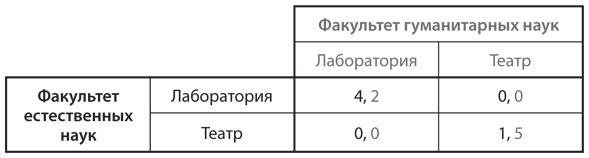
a) Каковы равновесия Нэша в чистых стратегиях в этой игре?
b) Какая из игр, представленных в данной главе, больше всего напоминает эту игру? Объясните логику своих рассуждений.
S9. Предположим, два участника игрового шоу, Алекс и Боб, каждый по отдельности выбирают двери с номерами 1, 2, 3. Оба игрока получают призы, если их выбор совпадает, как показано в следующей таблице:
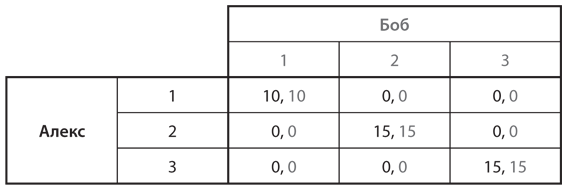
a) Каковы равновесия Нэша в этой игре? Какое из них (при его наличии) скорее всего приведет к (фокальному) исходу игры? Обоснуйте свой вывод.
b) Рассмотрите несколько измененную игру, в которой варианты выбора — снова просто числа, но две ячейки таблицы с выигрышами 15, 15 теперь содержат выигрыши 25, 25. Какой ожидаемый (средний) выигрыш каждого игрока, если каждый из них подбросит монету, чтобы решить, выбрать вариант 2 или 3? Лучше ли это фокусировки на том, чтобы оба выбрали 1 в качестве фокального равновесия? Как вам следует учитывать риск того, что Алекс может сделать одно, а Боб — другое?
S10. У Марты три сына: Артуро, Бернардо и Карлос. Она находит разбитую лампу посреди гостиной и понимает, что это сделал кто-то из сыновей. На самом деле виновник произошедшего Карлос, но Марта об этом не знает. Она заинтересована скорее в том, чтобы выяснить истину, а не наказать ребенка, поэтому предлагает сыновьям сыграть в следующую игру.
Каждый из них напишет на листе бумаги свое имя, а также слова: «Да, это я разбил лампу» либо «Нет, я не разбивал лампу». Если хотя бы один ребенок признается, что разбил лампу, Марта даст по 2 доллара (обычную сумму карманных денег) каждому, кто скажет, что разбил лампу, и 5 долларов тому, кто будет утверждать, что не делал этого. Если все три сына откажутся сознаваться, ни один из них не получит карманных денег (то есть каждый получит 0 долларов).
a) Составьте таблицу игры. Пусть Артуро соответствует строка таблицы, Бернардо — столбец, а Карлосу — страница.
b) Найдите все равновесия Нэша в этой игре.
c) В этой игре множество равновесий Нэша. Какое из них вы назвали бы фокальной точкой?
S11. Рассмотрите игру, в которой на кону стоит приз в размере 30 долларов. В ней три участника — Ларри, Керли и Мо. Каждый из них может купить (или нет) билет стоимостью 15 или 30 долларов. Игроки делают выбор одновременно и независимо друг от друга. Затем, собрав информацию о решениях игроков по поводу покупки билетов, организатор игры присуждает приз. Если никто не купит билет, приз не присуждается. В противном случае приз вручается тому, кто купил самый дорогой билет, если такой человек всего один, и делится поровну между двумя или тремя игроками, если они купили самые дорогие билеты по одной цене. Представьте эту игру в стратегической форме, включив в нее Ларри в качестве игрока, которому соответствуют строки, Керли — столбцы, а Мо — страницы. Найдите все равновесия Нэша в чистых стратегиях.
S12. Анна и Брюс намерены взять напрокат фильм, но не могут решить, какой именно. Анна хочет комедию, в Брюс — драму. Они решают сделать выбор случайным образом, сыграв в игру «чет или нечет». На счет три каждый из них выбрасывает один или два пальца. Если сумма пальцев представляет собой четное число, побеждает Энн и они берут напрокат комедию, если нечетное, то выигрывает Брюс и они смотрят драму. Каждый игрок получает выигрыш 1 за победу и 0 за проигрыш в игре «чет или нечет».
a) Нарисуйте таблицу игры «чет или нечет».
b) Покажите, что в этой игре нет равновесия Нэша в чистых стратегиях.
S13. В фильме «Игры разума» Джон Нэш и трое его коллег по магистратуре, придя в бар, сталкиваются с дилеммой. В баре находятся четыре брюнетки и одна блондинка. Каждый молодой человек хочет подойти и привлечь внимание одной из девушек. Выигрыш каждого за блондинку составляет 10, за брюнетку — 5, а если кто-то вообще останется без девушки, то 0. Проблема в том, что, если сразу несколько парней подойдут к блондинке, она отвергнет их всех, после чего брюнетки тоже их отвергнут, поскольку не хотят быть вторыми в очереди. Таким образом, каждый игрок получит выигрыш 10 только в случае, если окажется единственным претендентом на внимание блондинки.
a) Сначала упростите ситуацию, заменив четырех парней двумя, и проанализируйте ее. (В баре две брюнетки и одна блондинка, но девушки просто реагируют на действия парней вышеописанным образом и не являются активными участницами игры.) Составьте таблицу выигрышей для этой игры и найдите все равновесия Нэша в чистых стратегиях, присутствующие в ней.
b) Теперь постройте трехмерную таблицу для случая, когда в игре участвуют три молодых человека (а также три брюнетки и одна блондинка, которые не являются активными игроками). Снова найдите в ней равновесия Нэша.
c) Не прибегая к таблице, назовите все равновесия Нэша для изначальной ситуации.
d) (дополнительное упражнение). Используйте результаты, полученные в пунктах а, b и c, чтобы обобщить анализ на ситуацию, когда в игре участвуют n молодых людей. Не пытайтесь строить n-мерную таблицу выигрышей, просто вычислите выигрыш одного игрока в случае, если k других игроков выберут блондинку и (n – k – 1) выберут брюнетку, при k = 0, 1, ... (n – 1). Может ли исход, указанный в фильме в качестве равновесия Нэша (когда все молодые люди подойдут к брюнеткам), быть действительно равновесием Нэша в данной игре?
Упражнения без решений
U1. Найдите все равновесия Нэша в чистых стратегиях для представленных ниже игр. Сначала проверьте таблицу игры на наличие доминирующих стратегий. Если таковых нет, решите игру посредством итеративного исключения доминируемых стратегий.
a)
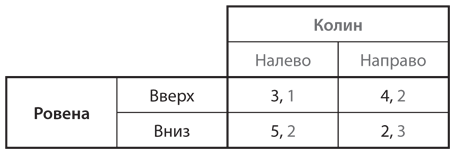
b)
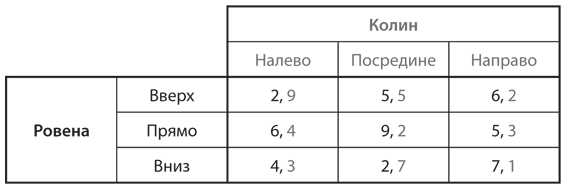
c)
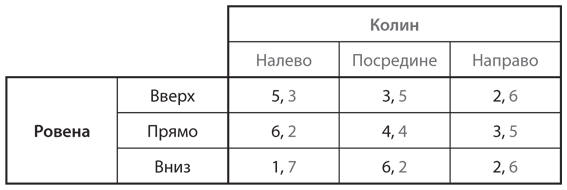
b)
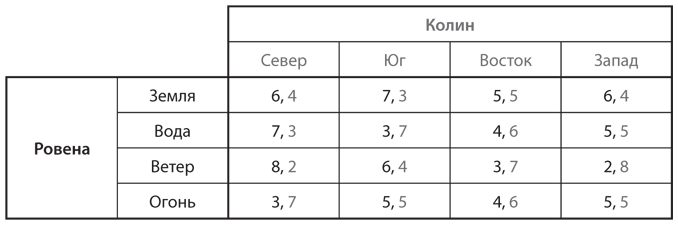
U2. Для каждой из четырех игр, представленных в упражнении U1, определите, это игра с нулевой или с ненулевой суммой. Объясните логику своих рассуждений.
U3. Как и в , используйте метод минимакса для поиска равновесий Нэша в играх с нулевой суммой, найденных в упражнении U2.
U4. Найдите все равновесия Нэша в чистых стратегиях в следующих играх. Опишите шаги, которые вы при этом предпринимали.
a)
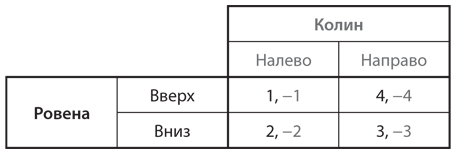
b)
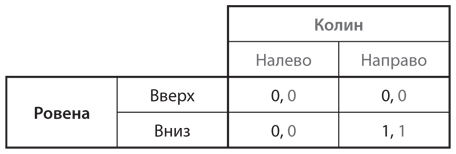
c)
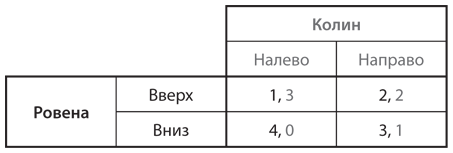
b)
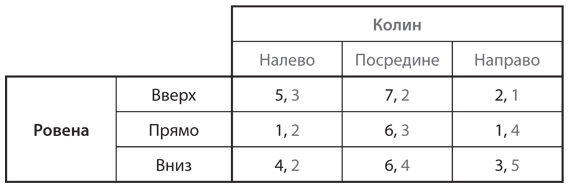
U5. Используйте метод последовательного исключения доминируемых стратегий для решения следующей игры. Опишите шаги, которые вы для этого предприняли. Покажите, что ваше решение представляет собой равновесие Нэша.
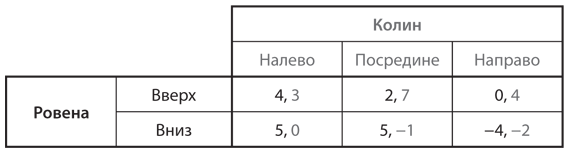
U6. Найдите все равновесия Нэша в чистых стратегиях для следующей игры. Опишите процесс, который вы при этом использовали. Объясните на примере данной игры, почему важно описывать равновесие с применением стратегий, выбранных игроками, а не только выигрышей, полученных в таком равновесии.
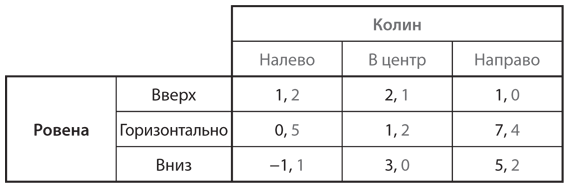
U7. Проанализируйте следующую таблицу игры:
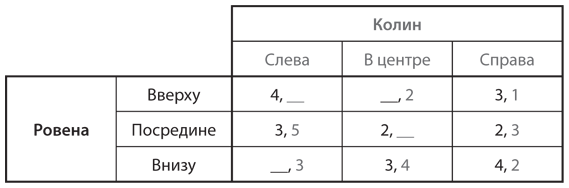
a) Проставьте недостающие выигрыши в таблице таким образом, чтобы у Колина была доминирующая стратегия. Укажите, какая стратегия доминирующая, и объясните почему. (Обратите внимание: существует много в равной степени правильных ответов.)
b) Проставьте недостающие выигрыши в таблице таким образом, чтобы ни у одного игрока не было доминирующей стратегии, но при этом у каждого была доминируемая стратегия. Укажите, какие стратегии доминируемые, и объясните почему. (В этом случае тоже существует много в равной степени правильных ответов.)
U8. Битва в море Бисмарка (по названию моря в юго-западной части Тихого океана, отделяющего архипелаг Бисмарка от Папуа — Новой Гвинеи) представляла собой морское сражение между Соединенными Штатами и Японией во время Второй мировой войны. В 1943 году японский адмирал получил приказ провести конвой кораблей в Новую Гвинею. Ему предстояло сделать выбор между дождливым северным маршрутом и более солнечным южным, каждый из которых требовал трех дней плавания. Американцы знали об отплытии конвоя и хотели послать вслед за ним бомбардировщики, но им не было известно, по какому пути отправится конвой. Американцам пришлось послать самолеты-разведчики на поиски конвоя, но их хватало только на изучение одного маршрута за один раз. И американцам, и японцам приходилось принимать решения, не имея никакой информации о планах другой стороны.
Если бы конвой оказался на маршруте, который американцы исследовали первым, они сразу же послали бы туда бомбардировщики, в противном случае они потеряли бы день. Кроме того, плохая погода на северном маршруте тоже затрудняла бомбардировку. Если бы американцы изучили северный маршрут и сразу же обнаружили японцев, они могли бы рассчитывать только на два (из трех) благоприятных дня для бомбардировки; если бы при изучении северного маршрута они обнаружили, что японцы ушли на юг, они тоже могли бы рассчитывать на два дня бомбардировки. Если бы американцы решили сначала исследовать южный маршрут, они могли бы рассчитывать на три полных благоприятных дня для бомбардировки, если бы обнаружили японцев сразу же, и только на один день, если бы увидели, что японцы предпочли северный маршрут.
a) Представьте эту игру в виде таблицы игры.
b) Определите в ней все доминирующие стратегии и вычислите равновесие Нэша.
U9. Двух игроков, Джека и Джилл, поместили в разные комнаты. Затем каждому из них объяснили правила игры. Каждый должен выбрать одну из шести букв: G, K, L, Q, R и W. Если случится так, что оба выберут одну и ту же букву, они получат призы по следующей схеме.

При выборе разных букв каждый игрок получит 0. Всю эту схему доводят до сведения игроков, и обоим говорят, что они оба знают эту схему.
a) Составьте таблицу этой игры. Каковы равновесия Нэша в чистых стратегиях?
b) Может ли одно из равновесий быть фокальной точкой? Какое? Почему?
U10. Три подруги (Джулия, Кристин и Лариса) независимо друг от друга идут покупать платья для выпускного бала. В магазине каждая девушка видит только три платья, которые достойны внимания: черное, бледно-лиловое и желтое. Более того, каждая девушка готова утверждать, что двух ее подруг тоже заинтересовал бы именно этот набор платьев, поскольку у всех троих примерно одинаковые вкусы.
Каждая девушка хотела бы надеть на выпускной бал единственное в своем роде платье, поэтому для нее полезность платья равна 0, если она купит одинаковое платье с кем-то из подруг. Все трое знают, что Джулия однозначно отдаст предпочтение черному перед бледно-лиловым и желтым цветом, поэтому она получила бы полезность 3, если бы была единственной девушкой в черном платье, и полезность 1, если бы только у нее было платье бледно-лилового или желтого цвета. Точно так же все трое знают, что Кристин нравится бледно-лиловый цвет и только во вторую очередь желтый, поэтому ее полезность составила бы 3, если бы только она надела бледно-лиловое платье, 2 — желтое и 1 — черное. И наконец, всем известно, что Лариса обожает желтый, а затем черный, поэтому она получила бы 3, если бы выбрала желтое платье, 2 — черное и 1 — бледно-лиловое.
a) Составьте таблицу для этой игры с участием трех игроков. Пусть Джулии соответствуют строки таблицы, Кристин — столбцы, Ларисе — страницы.
b) Определите все доминируемые стратегии в игре или объясните причину их отсутствия.
c) Каковы равновесия Нэша в чистых стратегиях в этой игре?
U11. Брюс, Колин и Дэвид собираются в доме Дэвида в пятницу вечером, чтобы поиграть в «Монополию». Все трое любят есть суши во время игры. По предыдущему опыту они знают, что двух порций суши вполне достаточно, чтобы утолить голод. Если они закажут меньше двух порций, то останутся голодными и не получат удовольствия от вечера, заказывать больше двух порций тоже не имеет смысла, поскольку они столько не съедят и третья порция испортится. Их любимый ресторан Fishes in the Raw упаковывает суши в такие большие контейнеры, что один человек может купить максимум одну порцию. Ресторан Fishes in the Raw предлагает суши навынос, но, к сожалению, не осуществляет доставку.
Предположим, полезность достаточного количества суши составляет для каждого игрока 20 долларов, а недостаточного — 0 долларов. Каждому игроку, который забирает заказ суши, это обходится в 10 долларов.
К сожалению, друзья забыли договориться о том, кто будет покупать суши в эту пятницу, и у них нет мобильных телефонов, поэтому они должны независимо друг от друга решить, покупать суши (П) или нет (Н).
a) Опишите эту игру в стратегической форме.
b) Найдите все равновесия Нэша в чистых стратегиях.
c) Какое равновесие вы назвали бы фокальной точкой? Объясните логику своих рассуждений.
U12. Роксанна, Сара и Тед очень любят печенье, но в упаковке осталось только одно. Никто не хочет делить его на части, поэтому Сара предлагает сыграть в следующий вариант игры «чет или нечет» (см. ), для того чтобы определить, кто съест печенье. На счет три каждый игрок выбрасывает один или два пальца, затем игроки их суммируют и делят сумму на 3. Если остаток 0, печенье достается Роксанне, если 1, то Саре, а если 2, то Теду. Каждый из игроков получает выигрыш 1, если победит (и съест печенье), и 0 в противном случае.
a) Представьте эту игру с тремя участниками в форме таблицы, где Роксанне соответствуют строки, Саре — столбцы, Теду — страницы.
b) Найдите все равновесия Нэша в чистых стратегиях. Можно ли назвать эту игру справедливым способом поделить печенье? Объясните, почему да или нет.
U13 (дополнительное упражнение). Постройте матрицу выигрышей для игры с двумя участниками, удовлетворяющей следующим требованиям. Во-первых, у каждого игрока должно быть три стратегии. Во-вторых, в игре не должны отсутствовать доминирующие стратегии. В-третьих, игра не должна быть разрешима методом минимакса. В-четвертых, в игре должно быть ровно два равновесия Нэша в чистых стратегиях. Составьте матрицу игры, а затем продемонстрируйте, что все перечисленные выше условия соблюдены.

