17 Переговоры
Люди ведут переговоры на протяжении всей своей жизни. Будучи детьми, они договариваются делиться игрушками и играть в игры со сверстниками. Став взрослыми и создав семью, договариваются о распределении домашних обязанностей, воспитании детей и коррективах, которые должен внести каждый в свою жизнь ради карьеры другого. Покупатели и продавцы торгуются о цене, работники и руководители договариваются о заработной плате. Страны ведут переговоры о политике взаимной либерализации торговли; сверхдержавы обсуждают взаимное сокращение вооружений. А двум первым авторам этой книги пришлось договариваться (в целом весьма дружелюбно), что в нее включать или не включать, как структурировать подачу материала и т. д. Для того чтобы получить приемлемый результат в ходе переговоров, их участники должны разработать эффективные стратегии. В данной главе описываются и подробно анализируются некоторые из таких базовых идей и стратегий.
У всех переговорных ситуаций есть две общие черты. Во-первых, суммарный выигрыш, который стороны переговоров могут обеспечить в результате достижения консенсуса, должен быть больше индивидуальных выигрышей, которые они могли бы получить по отдельности, то есть целое должно превышать сумму составляющих. При отсутствии такой избыточной ценности, или «излишка», проведение переговоров бессмысленно. Если двое детей, намеревающихся играть вместе, не видят чистой выгоды от получения доступа к большему количеству игрушек или от совместной игры, то каждому из них лучше забрать свои игрушки и играть самому. Мир полон неопределенности, поэтому ожидаемая выгода может не материализоваться. Но в процессе переговоров стороны должны по крайней мере рассчитывать на некоторые выгоды, которые можно извлечь из достигнутой договоренности: когда Фауст согласился продать душу дьяволу, он считал, что преимущества от обретенных им знаний и власти заслуживают той цены, которую ему пришлось в итоге заплатить.
Вторая важная общая черта переговоров вытекает из первой: переговоры не игра с нулевой суммой. При наличии излишка они сводятся к его разделению. Каждая сторона переговоров пытается выторговать больше для себя и оставить меньше всем остальным. На первый взгляд эта ситуация может показаться игрой с нулевой суммой, но здесь существует опасность того, что, если договоренность не будет достигнута, ни одна сторона не получит никаких излишков. Именно эта обоюдно пагубная альтернатива, а также стремление обеих сторон избежать ее создают почву для угроз (явных и скрытых), которые и делают переговоры вопросом стратегии.
До появления теории игр переговоры один на один считались трудной, а порой неразрешимой задачей. Наблюдение совершенно разных результатов в примерно схожих ситуациях подтверждало эту точку зрения. Теоретики не могли на системном уровне понять, почему одна сторона переговоров получает больше другой, и относили это на счет расплывчатых и необъяснимых различий в так называемой силе переговорной позиции.
Даже элементарная теория равновесия Нэша не позволяла продвинуться дальше. Предположим, два человека делят между собой 1 доллар. Давайте построим игру так, чтобы каждый из них объявлял о том, сколько он хотел бы получить. Ходы в игре делаются одновременно. Если объявленные игроками числа x и y в сумме не больше 1, каждый получает то, что огласил. Если сумма этих чисел больше 1, игроки не получают ничего. Стало быть, любая пара (x, y), дающая в сумме 1, образует в этой игре равновесие Нэша: с учетом намерений, анонсированных другим игроком, каждый игрок может извлечь для себя выгоду, только придерживаясь собственных заявлений.
Дальнейшее развитие теории игр проходило по двум разным направлениям, в каждом из которых использовалась своя логика теоретико-игровых рассуждений. В мы провели различие между теорией кооперативных игр, когда игроки выбирают и реализуют свои действия совместными усилиями, и теорией некооперативных игр, когда игроки выбирают и реализуют свои действия по отдельности. В каждом из направлений развития теории переговоров используется один из этих двух подходов. Один подход рассматривает переговоры как кооперативную игру, в которой переговорщики вместе находят и реализуют решение, возможно, с привлечением третьей стороны в качестве третейского судьи. Другой подход рассматривает переговоры как некооперативную игру, в которой переговорщики выбирают стратегии по отдельности и ищут равновесие. Однако, в отличие от приведенного выше простого примера с одновременным объявлением намерений, где равновесие было неопределенным, здесь мы вводим более структурированную игру с одновременными ходами и наличием предложений с обеих сторон, которая приводит к формированию детерминированного равновесия. Обращаем ваше внимание, что, как и в , терминами «кооперативный» и «некооперативный» обозначаются совместные и разрозненные действия, а не хорошее и плохое поведение или достижение компромисса в отличие от срыва переговоров. Равновесие в некооперативных переговорных играх может повлечь за собой множество компромиссов.
1. Кооперативное решение Нэша
В этом разделе мы проанализируем подход Нэша к переговорам как к кооперативной игре. Сначала представим эту идею в виде простого числового примера, а затем дадим ее более общее алгебраическое описание.
А. Числовой пример
Представьте двух предпринимателей из Кремниевой долины, Энди и Билла. Энди выпускает микросхему, которую может продавать любому производителю компьютеров по 900 долларов, а Билл разработал пакет программ, который может стоить 100 долларов. Они знакомятся и, немного пообщавшись, понимают, что их продукты идеально подходят друг к другу и что после незначительной доработки они могут выпускать комплексную систему аппаратного и программного обеспечения стоимостью 3000 долларов на каждый компьютер. Следовательно, объединившись, Энди и Билл могут создать дополнительную стоимость в размере 2000 долларов на единицу продукции и рассчитывают на продажу миллионов таких единиц в год. Единственное препятствие на пути к богатству — как его поделить? 3000 долларов — доход от каждой единицы, какую их часть должен получить Энди и какую Билл?
Главный аргумент Билла, что без его программного обеспечения микросхемы Энди — не более чем груда металла и песка, поэтому Энди должен получить 900 долларов, а сам Билл 2100 долларов. Энди парирует, что без его аппаратного обеспечения программы Билла — не более чем символы на бумаге или магнитные сигналы на диске, поэтому Билл должен получить всего 100 долларов, а остальные 2900 долларов — он, Энди.
Наблюдая за этим спором, вы могли бы посоветовать им разделить разницу между собой. Однако это не совсем точный рецепт достижения соглашения. Билл мог бы предложить Энди поровну разделить прибыль с каждой единицы продукции. При такой схеме каждый получит прибыль в размере 1000 долларов, то есть 1100 долларов дохода достанется Биллу и 1900 долларов Энди. Встречное предложение Энди может состоять в том, что каждый должен получить равный процент прибыли на вклад в совместное предприятие. Тогда Энди получит 2700 долларов, а Билл 300 долларов.
Если Энди и Билл ведут переговоры непосредственно между собой, окончательное соглашение зависит от настойчивости или терпения обоих. Если же они попытаются прибегнуть к помощи третейского судьи, то его решение зависит от понимания относительной стоимости аппаратного и программного обеспечения, а также от навыков риторики, которые используют два принципала в процессе представления ему своих аргументов. Для определенности давайте предположим, что третейский судья предлагает разделить прибыль в соотношении 4:1 в пользу Энди, то есть Энди должен получить четыре пятых от излишка, тогда как Билл одну пятую, или Энди должен получить в четыре раза больше, чем Билл. Каким будет фактическое разделение дохода по такой схеме? Допустим, общий доход Энди x, а Билла — y; тогда прибыль Энди составит (x – 900), а Билла — (y – 100). Решение третейского судьи подразумевает, что прибыль Энди должна в четыре раза превышать прибыль Билла; следовательно, x – 900 = 4(y – 100), или x = 4y + 500. Общий доход обоих предпринимателей равен 3000 долларов, стало быть, должно выполняться равенство x + y = 3000, или x = 3000 – y. В таком случае x = 4y + 500 = 3000 – y, или 5y = 2500, или y = 500, а значит, x = 2500. Такой механизм разделения прибыли обеспечивает Энди 2500 – 900 = 1600 долларов, а Биллу 500 – 100 = 400 долларов, что равносильно разделению прибыли в соотношении 4:1 в пользу Энди, о котором говорит третейский судья.
На основании этих элементарных данных мы выведем алгебраическую формулу, которую вы найдете весьма полезной во многих практических приложениях, а затем перейдем к анализу других факторов, от которых зависят пропорции разделения прибыли в переговорной игре.
Б. Общая теория
Предположим, два участника переговоров, A и Б, пытаются разделить общую величину v, которую они могут получить, только если договорятся о конкретном способе разделения. Если соглашение не будет достигнуто, А получит a, а Б получит b, причем каждый будет действовать в одиночку или каким-то иным способом вне пределов их отношений. Назовем эти показатели страховочными выигрышами, или, используя терминологию Гарвардского переговорного проекта, их лучшими альтернативами обсуждаемому соглашению (best alternative to a negotiated agreement, BATNA). Зачастую значения a и b равны нулю, но в более общем плане будем исходить из того, что a + b < v, то есть данное соглашение обеспечивает положительный излишек (v – a – b); в противном случае весь переговорный процесс оказался бы бессмысленным, поскольку каждая сторона просто воспользовалась бы внешней возможностью и получила бы свой BATNA.
Рассмотрим следующее правило: каждому игроку необходимо предоставить его BATNA и долю излишка. Допустим, для А доля излишка равна h, а для Б — k, причем h + k = 1. Выразив x в виде суммы, которую получит в итоге А, а y — в виде суммы, которую получит в итоге Б, имеем
x = a + h(v – a – b) = a(1 – h) + h(v – b), x – a = h(v – a – b),
а также
y = b + k(v – a – b) = b(1 – k) + k(v – a), y – b = k(v – a – b).
Мы называем эти выражения формулами Нэша. Еще один способ интерпретировать их сводится к такому утверждению: излишек (v – a – b) подлежит разделению между двумя участниками переговоров в соотношении h к k, или
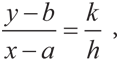
или в виде уравнения
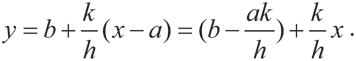
Для того чтобы охватить весь излишек, x и y должны также удовлетворять уравнению x + y = v. Формулы Нэша для x и y — это и есть решения системы последних двух уравнений.
Геометрическое представление кооперативного решения Нэша приведено на рис. 17.1. Страховочный выигрыш, или BATNA, находится в точке P с координатами (a, b). Все точки (x, y), которые делят прибыль между двумя игроками в соотношении h к k, лежат на прямой линии, которая проходит через точку P и имеет наклон k/h; эта наклонная прямая представляет собой график функции y = b + (k/h)(x – a), которую мы вывели ранее. Все точки (x, y), охватывающие весь излишек, лежат на прямой, проходящей через точки (v, 0) и (0, v); эта прямая соответствует второму уравнению, полученному выше, а именно x + y = v. Решение Нэша находится в точке пересечения этих линий, то есть в точке Q. Координаты этой точки — выигрыши сторон после достижения соглашения.
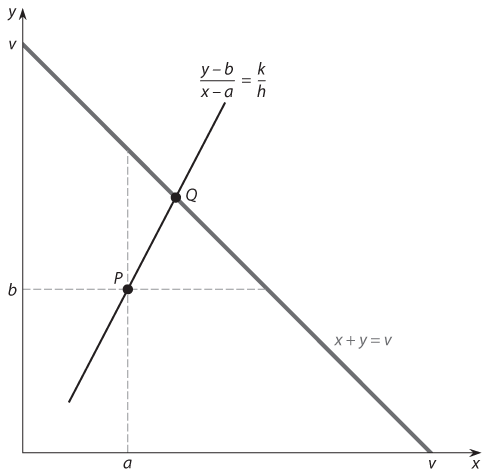
Рис. 17.1. Решение Нэша для переговорной игры в простейшем виде
Формула Нэша ничего не говорит о том, как может быть получено это решение. И такая расплывчатость — ее преимущество, поскольку ее можно использовать для описания результатов множества разных теорий с учетом множества разных подходов.
На простейшем уровне формулу Нэша можно рассматривать как краткое описание результата переговорного процесса, который мы не оговаривали в деталях. Тогда h и k могут обозначать относительную силу переговорных позиций сторон. Такое сокращенное описание представляет собой компромисс; более полная теория должна объяснять, откуда берется сила переговорных позиций и почему у одной стороны она может быть больше, чем у другой. Мы сделаем это в конкретном контексте ниже в данной главе, а пока эта формула дает нам хороший инструмент, отображая все без исключения источники силы переговорных позиций в показателях h и k.
Сам Нэш придерживался иного подхода, отличающегося от подхода к теории игр, используемого нами до сих пор в данной книге. Поэтому его подход заслуживает более тщательного объяснения. Во всех уже изученных нами играх участники выбирали и разыгрывали свои стратегии отдельно друг от друга. Мы искали равновесия, в которых стратегия каждого игрока отвечала его собственным интересам с учетом стратегий других игроков. Порой такие исходы были весьма неблагоприятны для некоторых, а то и всех участников игры, чему наглядный пример — дилемма заключенных. Тогда у игроков была возможность собраться вместе и договориться следовать определенной стратегии. Но в нашей системе у них не было никакого способа проконтролировать выполнение достигнутого соглашения. Договорившись, игроки расходились, а когда наступала их очередь действовать, они делали то, что максимально отвечало их собственным интересам. Под влиянием столь разрозненных стремлений игроки нарушали соглашение о совместных действиях. Правда, в ходе анализа повторяющихся игр в мы обнаружили, что скрытая угроза разрыва длительных отношений способна поддерживать выполнение договоренности, а в допустили возможность коммуникации посредством подачи сигналов. Однако значение имело именно индивидуальное действие, а любая взаимная выгода достигалась только тогда, когда ей не грозило пасть жертвой эгоистичности разрозненных действий отдельных игроков. В мы назвали такой подход к теории игр некооперативным, подчеркнув, что этот термин указывает на способ выполнения действий, а не на то, станет ли их результат приемлемым для всех игроков. Опять же, важно то, что любое совместное благо должно представлять равновесный результат разрозненных действий в подобных играх.
Но что если совместные действия все же возможны? Например, участники игры могут совершить их сразу же после достижения договоренностей, в присутствии друг друга. Или могут делегировать реализацию соглашения нейтральной третьей стороне или посреднику. Другими словами, игра может быть кооперативной (снова в смысле совместных действий). Нэш моделировал переговорный процесс именно в виде кооперативной игры.
Рассуждения коллектива, планирующего реализовать совместное соглашение посредством совместных действий, могут существенно отличаться от рассуждений совокупности отдельных людей, которые знают, что взаимодействуют стратегически, но совершают при этом некооперативные действия. В то время как члены второй группы будут думать в категориях равновесия, а затем либо радоваться, либо огорчаться, в зависимости от удовлетворенности полученными результатами, члены первой группы сначала подумают о том, какой результат будет приемлемым, а затем посмотрят, как его достичь. Иными словами, теория определяет исход кооперативной игры с точки зрения ряда общих принципов или свойств, которые считает разумными ее автор.
Нэш сформулировал ряд таких принципов для переговоров и доказал, что они подразумевают единственный исход. Вот их примерное описание: 1) этот исход должен быть инвариантным, если шкала измерения выигрышей меняется линейно; 2) он должен быть эффективным; 3) на него не повлияет сокращение множества возможных вариантов путем удаления тех, которые в любом случае не будут выбраны.
Первый принцип согласуется с теорией ожидаемой полезности, которую мы вкратце рассматривали в . Там мы увидели, что нелинейная шкала выигрышей отображает изменения отношения игрока к риску и реальное изменение линии поведения: вогнутая шкала подразумевает нерасположенность к риску, а выгнутая — склонность к риску. Линейная шкала, будучи промежуточными вариантом, отображает нейтральность к риску. Следовательно, линейное изменение шкалы выигрышей не влияет на оценку ожидаемых выигрышей и не сказывается на полученных результатах.
Второй принцип означает, что ни одна часть имеющейся взаимной выгоды не должна оставаться неиспользованной. В нашем простом примере, где игроки А и Б делят общую величину v, это означало бы, что x и y должны составлять в сумме всю имеющуюся величину v, но ни в коем случае не меньше v, то есть решение должно лежать на линии x + y = v, представленной на . В более общем случае полный набор логически возможных соглашений в переговорной игре, отображенных в виде графика на , будет ограничен сверху и справа подмножеством соглашений, которые не оставляют неиспользованной ни одну долю взаимной выгоды. Это подмножество не обязательно должно располагаться на прямой, такой как x + y = v (или y = v – x); оно может находиться на любой линии в форме y = f(x).
На рис. 17.2 все точки над и под (то есть к «югу» и к «западу») кривой y = f(x), представленной в виде жирной серой линии, образуют полное множество возможных исходов. Сама кривая состоит из эффективных исходов: не существует возможных исходов, которые включали бы больше значений x и y, чем исходы на кривой y = f(x), а значит, неиспользованной взаимной выгоды нет. В связи с этим мы называем кривую y = f(x) эффективной границей в переговорной задаче.
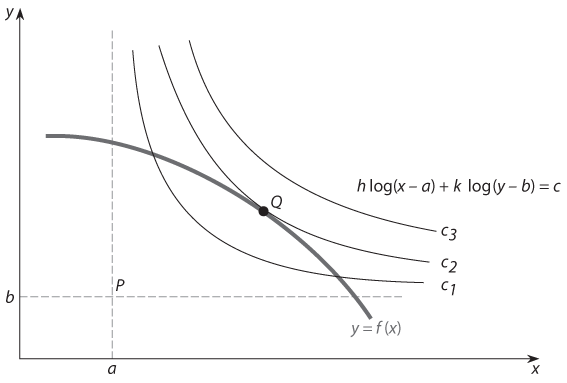
Рис. 17.2. Общий вид решения Нэша для переговорной игры
Мы можем проиллюстрировать изогнутую эффективную границу на примере рационального распределения риска из . Два фермера, функция полезности каждого из которых выражена в виде квадратного корня, сталкиваются с риском того, что в равной степени вероятные благоприятные или неблагоприятные условия обеспечат им либо 160 000, либо 40 000 долларов дохода, что даст каждому из них ожидаемую полезность в размере
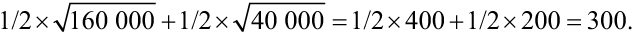
Однако между рисками этих двух фермеров присутствует идеальная отрицательная корреляция. У одного складываются хорошие погодные условия, тогда как у другого плохие, а значит, их совокупный доход составит 200 000 долларов независимо от того, какому фермеру с погодой повезет. Если фермеры договорятся, что первый из них получит долю совокупного дохода z, а второй — оставшийся доход (200 000 – z), то их значения полезности x и y соответственно составят
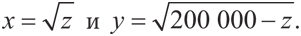
Стало быть, мы можем описать множество возможных исходов разделения риска с помощью уравнения
x2 + y2 = z + (200 000 – z) = 200 000.
Это уравнение описывает четверть окружности в положительном квадранте и отображает эффективную границу переговорной задачи двух фермеров. Показатель BATNA каждого фермера — это ожидаемая полезность 300, которую он будет иметь, если фермеры не достигнут соглашения по разделению риска. Подставив данное значение в уравнение, получаем 3002 + 3002 = 90 000 + 90 000 = 180 000 < 200 000. Следовательно, точка, соответствующая значению BATNA, находится с внутренней стороны четверти окружности эффективной границы.
Третий принцип также весьма интересен. Если исход, который участник переговоров в любом случае бы не выбрал, исключается из рассмотрения, тогда какое он имеет значение? Это предположение тесно связано с условием независимости от посторонних альтернатив в теореме о невозможности Эрроу, о которой шла речь в , но нам придется оставить эту связь для более сложных работ по данной теме.
Нэш доказал, что кооперативный исход, удовлетворяющий всем трем предположениям, можно описать в виде математической задачи максимизации: выберите такие значения x и y, которые обеспечат максимум функции (x – a)h(y – b)k при условии y = f(x).
Здесь x и y — исходы, a и b — страховочные выигрыши, а h и k — два возможных числа, составляющих в сумме 1, которые аналогичны силе переговорных позиций в формуле Нэша. Значения h и k не могут быть определены только посредством трех исходных предположений Нэша; следовательно, они оставляют некоторую степень свободы в теории и в результатах. В действительности Нэш ввел в эту задачу четвертое предположение — о симметрии между двумя игроками. Оно привело к результату h = k = 1/2 и позволило найти единственное решение. Мы дали более общую формулировку, впоследствии получившую широкое распространение в теории игр и экономике.
На дано геометрическое представление цели максимизации. Черные линии, обозначенные как c1, c2 и c3 — это изолинии, или линии уровня максимизируемой функции; на каждой такой кривой значение (x – a)h(y – b)k представляет собой постоянную величину и составляет c1, c2 и c3 (где c1 < c2 < c3), как показано выше. Все пространство можно заполнить такими линиями, у каждой из которых свое значение постоянной, а у линий, расположенных в направлении «северо-востока», значения постоянных выше.
Очевидно, что самое высокое из возможных значение данной функции находится в точке касания Q линии эффективной границы и одной из изолиний. Местоположение точки Q определяется тем свойством, что линия уровня, проходящая через Q, — касательная к линии эффективной границы. Точка касания — это общепринятый способ представления кооперативного решения Нэша в геометрическом виде.
В примере на также можно вывести решение Нэша математически; для этого понадобится дифференциальное исчисление, но цели важнее способов их достижения (во всяком случае, в контексте изучения стратегических игр). Для того чтобы найти это решение, целесообразно записать X = x – a и Y = y – b. Таким образом, X — это величина излишка, получаемого игроком А, а Y — величина излишка игрока Б. Условие эффективности исхода гарантирует, что X + Y = x + y – a – b = v – a – b, что и представлет собой общую величину излишка, которую мы обозначим символом S. Тогда Y = S – X, а также
(x – a)h(y – b)k = XhYk = Xh(S – X)k.
В решении Нэша X принимает значение, максимизирующее эту функцию. Элементарное исчисление говорит о том, что для определения значения X необходимо взять производную этого выражения по X и приравнять к нулю. Воспользовавшись правилами исчисления для поиска производных степеней X и произведения двух функций X, получим
hXh – 1(S – X)k – Xhk(S – X)k – 1 = 0.
Исключив общий множитель Xh – 1(S – X)k – 1, будем иметь
h(S – X) – kX = 0,
hY – kX = 0,
kX = hY
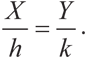
И наконец, выразив это уравнение через исходные переменные x и y, получим (x – a)/h = (y – b)/k, а это и есть формула Нэша. Вывод: три условия Нэша приводят к формуле, которую мы изначально обозначили как простой способ разделения излишка в процессе переговоров.
Эти три принципа, или заданные свойства, определяющие решение Нэша для кооперативных переговоров, — просты и даже привлекательны. Но при отсутствии эффективного способа убедиться, что стороны переговоров предпримут действия, предусмотренные в соглашении, они могут оказаться бесполезны. Игрок, которому выгоднее самостоятельно разрабатывать стратегию, чем использовать решение Нэша, может их просто проигнорировать. Если третейский судья может принудить выполнить решение, то игрок может отказаться от его услуг. Следовательно, кооперативное решение Нэша будет более убедительным при наличии альтернативной интерпретации в виде равновесия Нэша в некооперативной игре с двумя участниками переговоров. Это действительно осуществимо, и мы рассмотрим такой пример в .
2. Переговоры с переменной угрозой
В данном разделе мы используем кооперативное решение Нэша в конкретной игре, а именно на втором этапе игры с последовательными ходами. В мы исходили из предположения, что страховочные выигрыши игроков (BATNA) a и b имеют фиксированное значение. Но допустим, существует первый этап переговорной игры, на котором игроки могут выполнять стратегические ходы, направленные на манипулирование показателями BATNA в определенных пределах. После таких действий игроков на втором этапе игры появляется кооперативный исход Нэша. Игру данного типа называют переговорами с переменной угрозой. Какие манипуляции со значениями BATNA отвечают интересам ее участников?
На рис. 17.3 показаны возможные результаты манипулирования BATNA. Исходные значения страховочных выигрышей (a и b) — это координаты страховочной точки P в игре; решение Нэша в переговорной игре с такими страховочными выигрышами находится в точке Q. Если игрок А сможет увеличить значение BATNA так, чтобы переместить страховочную точку игры в позицию P1, то решение Нэша, начинающееся в этой точке, приведет к исходу Q´, что лучше для игрока А (но хуже для игрока Б). Следовательно, стратегический ход, улучшающий BATNA игрока, целесообразен. Например, если, идя на собеседование в другую компанию, вы уже имеете хорошее предложение о работе (более высокий показатель BATNA), то, по всей вероятности, получите от этого работодателя более выгодное предложение, чем при отсутствии первой альтернативы.
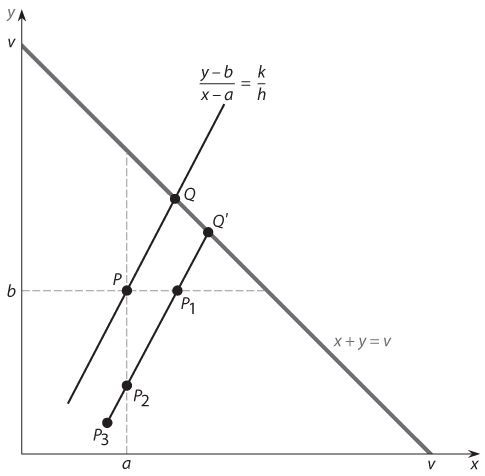
Рис. 17.3. Переговорная игра с манипулированием значениями BATNA
Вывод о том, что повышение BATNA может улучшить конечный результат, вполне очевиден, но следующий этап анализа менее понятен. Оказывается, если игрок А сможет сделать стратегический ход, который уменьшит BATNA игрока Б и переместит страховочную точку игры в точку P2, то решение Нэша, начинающееся в этой точке, приведет к тому же исходу Q´, который был получен, когда игрок А увеличил свой показатель BATNA настолько, что попал в страховочную точку P1. Следовательно, этот альтернативный тип манипуляции также отвечает интересам игрока А. В качестве примера уменьшения BATNA соперника представьте ситуацию, в которой вы уже работаете в компании и хотите получить повышение. Ваши шансы возрастут, если вы станете незаменимым для работодателя, то есть если без вас у его бизнеса возникнут проблемы. В таком случае неблагоприятный исход ввиду отсутствия соглашения (когда работодатель не предложит повышения и вы уволитесь из компании) может повысить вероятность того, что работодатель пойдет вам навстречу.
И последний, еще более драматичный вариант развития событий: если игрок А сможет сделать стратегический ход, уменьшающий значения BATNA обоих игроков настолько, что страховочная точка игры переместится в точку P3, это опять же приведет к тому же результату, что и вследствие предыдущих манипуляций. Этот ход равносилен угрозе, которая гласит: «Это навредит вам больше, чем мне».
В общем плане для игрока А важно переместить BATNA в данной игре в одну из точек, находящихся под линией PQ. Чем дальше на юго-восток передвинется точка BATNA, тем лучше для игрока А в свете конечного результата. Как всегда в случае применения угроз, задача не в получении низкого выигрыша, а в том, чтобы использовать его вероятность в качестве рычага для достижения более приемлемого исхода.
Возможность манипулировать BATNA таким способом зависит от контекста. Мы предлагаем один наглядный пример. В 1980 году проводилась забастовка бейсболистов, которая приняла весьма сложную форму. Игроки объявили ее во время весенних сборов, затем возобновили работу (то есть игру), когда в апреле стартовал регулярный сезон, а затем снова объявили забастовку начиная с Дня поминовения. Забастовка приносит убытки обеим сторонам (как работодателям, так и работникам), но они разнятся. Во время весенних сборов игроки не получают заработную плату, а владельцы команд немного зарабатывают за счет зрителей-отпускников. В начале регулярного сезона, в апреле и мае, бейсболисты получают заработную плату, но погода еще холодная и сезон не особо захватывающий, поэтому зрителей мало, а значит, владельцы команд несут не очень высокие издержки в связи с забастовкой. Начиная с Дня поминовения количество зрителей увеличивается, и издержки владельцев команд в связи с забастовкой возрастают, но заработная плата, которую могут потерять игроки, остается неизменной. Мы видим, что эта двухэтапная забастовка весьма изобретательно разработана так, чтобы максимально снизить BATNA владельцев команд относительно BATNA игроков.
Остается только одна загадка: почему забастовка вообще была объявлена? Согласно теории, все должны были понимать, чем это закончится; если бы конфликт был урегулирован на более приемлемых для бейсболистов условиях, забастовка вообще бы не понадобилась. И если она действительно проводится, то это угроза, с которой что-то «пошло не так». По всей вероятности, это можно отнести на счет некоторой неопределенности — асимметричности информации или балансирования на грани.
3. Чередующиеся предложения, модель I: убывание общей величины
В этом разделе мы вернемся к более реалистичной теории некооперативных игр и проанализируем процесс индивидуального построения стратегии, который может привести к формированию равновесия в переговорной игре. Наш стандартный подход к данному процессу — чередующиеся предложения. Один игрок (скажем, А) делает предложение, другой игрок (к примеру, Б) либо принимает его, либо делает встречное предложение. В случае последнего варианта игрок А может либо принять это предложение, либо сделать свое предложение и т. д. Таким образом, мы имеем игру с последовательными ходами и нам необходимо найти в ней равновесие обратных рассуждений.
Для этого следует начать с самого конца и выполнить обратный анализ. Но где именно находится конечная точка? Почему процесс взаимных предложений вообще должен закончиться? А вот еще более резонный вопрос: с какой стати он вообще должен начаться? Почему бы двум переговорщикам не придерживаться своих исходных позиций и не стоять на своем? Если они не смогут договориться, это будет чревато для обоих, но преимущества от достигнутого соглашения, скорее всего, окажутся меньше для того, кто сделает первую или большую уступку. По всей вероятности, причина капитуляции одного из участников переговоров заключается в том, что излишнее упорствование приведет к еще большей потере выгоды. Эта потеря принимает одну из общих форм. Имеющийся «пирог», или излишек, может убывать (уменьшаться) с каждым очередным предложением — мы проанализируем такой сценарий чуть позже. Альтернатива состоит в том, что время имеет свою цену, а нетерпение играет свою роль, поэтому ценность отложенного соглашения меньше; этот сценарий мы разберем в .
Рассмотрим следующую историю о переговорах по уменьшению «пирога». Болельщик приходит на матч по профессиональному футболу (или баскетболу) без билета и готов заплатить 25 долларов за просмотр каждой четверти матча. Болельщик находит спекулянта, который называет свою цену за билет. Если болельщик не готов ее заплатить, он пойдет в ближайший бар и посмотрит первую четверть на большом экране там. По окончании четверти он выйдет из бара, увидит того же спекулянта и сделает встречное предложение о цене билета. Если спекулянт не согласится, болельщик вернется в бар. После второй четверти матча он снова выйдет из бара, и спекулянт опять сделает ему очередное предложение. Если оно неприемлемо для болельщика, он вернется в бар, выйдет оттуда в конце третьей четверти и сделает еще одно встречное предложение. Стоимость просмотра оставшейся части матча снижается по мере окончания очередной четверти.
Анализ методом обратных рассуждений позволяет предсказать исход этого переговорного процесса с чередующимися предложениями. В конце третьей четверти болельщик знает, что, если он не купит билет, спекулянт останется с маленьким листиком бумаги, уже не представляющим никакой ценности. Следовательно, болельщик может предложить за билет очень маленькую цену, и для спекулянта это будет лучше, чем ничего. Таким образом, в случае последнего предложения болельщик получит билет практически бесплатно. Переместившись на один период назад, мы видим, что в конце второй четверти инициатива делать предложение переходит к спекулянту. Но он должен заглянуть вперед и понять, что не может рассчитывать на получение всей стоимости билета за оставшиеся две четверти матча. Если спекулянт назовет цену больше 25 долларов (такова стоимость третьей четверти для болельщика), болельщик не согласится, поскольку знает, что чуть позже сможет получить билет на четвертую четверть почти бесплатно. Стало быть, спекулянт должен установить цену не выше 25 долларов. Теперь проанализируем ситуацию в конце первой четверти. Болельщик знает, что, если не купит билет сейчас, впоследствии спекулянт может рассчитывать максимум на 25 долларов, а значит, 25 долларов и есть цена, которую болельщику следует предложить сейчас, чтобы гарантированно получить билет. И наконец, еще перед матчем спекулянт может проанализировать ситуацию и попросить за билет 50 долларов; эта цена включает стоимость первой четверти матча, составляющую 25 долларов, и стоимость оставшихся трех четвертей, также равную 25 долларам. Таким образом, болельщик и спекулянт сразу же ударят по рукам, и билет достанется болельщику за 50 долларов, но чтобы определить эту цену, понадобится пройти весь процесс анализа методом обратных рассуждений.
Эту историю можно без труда представить в виде более общих рассуждений в отношении переговоров между двумя участниками сделки, А и Б. Предположим, игрок А делает первое предложение о разделе общего излишка, который мы обозначим символом v (в какой-либо валюте, например в долларах). Если игрок Б отказывается его принять, общая имеющаяся сумма уменьшается на x1, до (v – x1), после чего игрок Б предлагает ее разделить. Если игрок А опять отказывается, общая сумма уменьшается уже на x2, до (v – x1 – x2), после чего игрок А предлагает ее разделить. Такой процесс взаимных предложений продолжается до тех пор, пока, скажем, после 10 раундов v – x1 – x2 – … – x10 = 0, после чего игра заканчивается. Как обычно в играх с последовательными ходами, начнем наш анализ с конца.
Если игра дошла до того момента, когда остается только x10, игрок Б может сделать последнее предложение, согласно которому он получает «почти весь» излишек, оставив игроку А жалкий цент или что-то около того. Поскольку у игрока А выбор только один — либо получить эту сумму, либо совсем ничего, ему следует принять предложение. Во избежание сложностей с кропотливым отслеживанием мизерных сумм, давайте обозначим этот исход так: «x10 игроку Б, 0 игроку А». То же самое сделаем и в других (более ранних) раундах.
Зная о том, что произойдет в раунде 10, переходим к раунду 9. Здесь игрок А должен сделать предложение, после чего остается (x9 + x10). Игрок А знает, что должен предложить игроку Б минимум x10, иначе тот отклонит предложение и переведет игру в раунд 10, где он сможет получить такую большую сумму. Игрок А не хочет предлагать игроку Б больше. Таким образом, в раунде 9 игрок А предложит разделить сумму так, чтобы ему досталась сумма x9, а игроку Б — x10.
Еще одним раундом ранее, когда остается x8 + x9 + x10, игрок Б предложит такое разделение, при котором он отдаст игроку А x9 и оставит себе (x8 + x10). Анализ методом обратных рассуждений позволяет сделать вывод, что в самом первом раунде игрок А предложит разделить сумму так, чтобы оставить себе (x1 + x3 + x5 + x7 + x9) и отдать (x2 + x4 + x6 + x8 + x10) игроку Б. Это предложение будет принято.
Эти формулы можно запомнить с помощью простого приема. Выстройте гипотетическую последовательность, в которой отклоняются все предложения. (На самом деле такая последовательность не соответствует действительности.) Затем сложите все суммы, которые были бы потеряны из-за отказов одного игрока. Это и есть то, что получает другой игрок в случае фактического равновесия. Например, когда игрок Б отказался принять первое предложение игрока А, общий имеющийся излишек уменьшился на x1 и сумма x1 стала частью того, что получил игрок А в равновесии этой игры.
Если у каждого игрока положительное значение BATNA, данный анализ необходимо несколько модифицировать с учетом этих значений. В последнем раунде игрок Б должен предложить игроку А сумму BATNA, равную a. Если x10 больше a, игроку Б достанется (x10 – a), если нет, игра должна завершиться до наступления этого раунда. Теперь в раунде 9 игрок А должен предложить игроку Б большую из двух сумм — сумму (x10 – a), которую игрок Б может получить в раунде 10, или сумму BATNA, равную b, которую игрок Б может получить за пределами данного соглашения. Этот анализ можно продолжить до раунда 1; мы предоставляем эту возможность вам: выполните его самостоятельно методом обратных рассуждений.
Итак, мы нашли равновесие обратных рассуждений в переговорной игре с чередующимися предложениями и в процессе его поиска описали полные стратегии (исчерпывающие условные планы действий), входящие в состав данного равновесия, а именно действия каждого игрока в случае, если бы игра перешла на более поздний этап. На самом деле соглашение достигается сразу же после внесения первого предложения. Более поздние этапы игры так и не наступают: они представляют собой узлы и пути, находящиеся за пределами равновесия. Но, как и всегда при использовании метода обратных рассуждений, в основе исходного действия лежит предположение о том, что игроки сделали бы в этих узлах, если бы дошли до них.
Следует отметить еще один важный момент: постепенное убывание (несколько раундов предложений) обеспечивает более равное или справедливое разделение общего выигрыша, чем резкое убывание (когда допускается только один раунд переговоров). Во втором случае соглашение не будет достигнуто, если игрок Б отклонит первое предложение игрока А; тогда в соответствии с равновесием обратных рассуждений игрок А попытается оставить себе (почти) весь излишек, в ультимативной форме предложив игроку Б согласиться на мизерную сумму, иначе тот вообще ничего не получит. Последующие раунды предоставляют игроку Б достоверную возможность отказаться от весьма несправедливого первого предложения.
4. Экспериментальные данные
Теория переговорного процесса данного типа достаточно проста, и многие исследователи провели лабораторные или аудиторные эксперименты, в которых воссоздавались условия переговорной игры с убыванием общей величины, чтобы понаблюдать за тем, что на самом деле будут делать испытуемые в подобной ситуации. Мы вкратце упомянули о таких экспериментах в в ходе анализа обоснованности метода обратных рассуждений, теперь же рассмотрим их более подробно в контексте переговоров.
Простейший эксперимент с переговорами — ультимативная игра, состоящая всего из одного раунда: игрок А делает предложение, и если игрок Б не принимает его, переговоры заканчиваются и оба ничего не получают. Общая структура организации таких игр следующая: группу игроков собирают либо в одном помещении, либо в сети у компьютеров и распределяют по парам, в которых один игрок становится предлагающим (то есть делает предложение или публикует цену), а другой выбирающим (то есть принимает или отклоняет предложение или решает, стоит ли покупать по такой цене). Паре предоставляется фиксированный излишек (как правило, 1 доллар или какая-то другая сумма), который предстоит разделить.
Согласно анализу методом обратных рассуждений, игрок А должен предложить игроку Б минимальную единицу (скажем, один цент), а игрок Б должен принять это предложение. Однако фактические результаты кардинально отличаются от теоретического вывода. Когда участники эксперимента находятся в одной комнате, а роль предлагающего присваивается случайным образом, испытуемые чаще всего предлагают разделить излишек в соотношении 50 на 50. При этом фиксируется очень мало предложений о разделении в пропорции 75 на 25 (75% предлагающему и 25% выбирающему), но даже если они и встречаются, их обычно отклоняют.
Такие результаты объясняются двумя причинами: либо игроки не могут или не хотят выполнять вычисления, необходимые для анализа методом обратных рассуждений, либо их выигрыши включают в себя нечто иное, чем то, что они получат в ходе этого раунда переговоров. Безусловно, расчеты в ультимативной игре настолько просты, что выполнить их может каждый, а участники большинства таких экспериментов, как правило, студенты университетов. Более вероятное объяснение — это то, которое мы уже выдвинули в и в : теория, исходящая из того, что выигрыши состоят исключительно из суммы, полученной только за один этот раунд переговоров, слишком упрощена и не учитывает ряда факторов.
Выигрыши участников экспериментов могут включать в себя нечто иное. У игроков может быть развито самоуважение или гордость, не позволяющая принимать столь неравное распределение излишка. Даже если предлагающий игрок А не включает этот фактор в собственный выигрыш, но считает, что игрок Б может исходить из него, то для игрока А выигрышной будет стратегия предложить такое разделение излишка, которое бы повысило вероятность того, что игрок Б примет предложение. Предлагающий игрок А взвешивает свой высокий выигрыш в случае предложения меньшей доли игроку Б на фоне риска того, что он может вообще ничего не получить, если игрок Б посчитает его предложение слишком несправедливым.
Еще одно объяснение сводится к тому, что когда участники эксперимента находятся в одном помещении, это не обеспечивает анонимность образования пар. И если испытуемые принадлежат к одной группе, такой как студенты университета или жители одной деревни, они могут высоко ценить отношения с другими членами группы вне рамок игры. В итоге предлагающие игроки опасаются, что предложение слишком неравного разделения излишка может негативно сказаться на этих отношениях. Поэтому они будут делать более щедрые предложения, чем предполагает теория. Если проблема именно в этом, то гарантия анонимности позволит предлагающим игрокам делать более неравные предложения, и результаты экспериментов подтверждают, что так и есть.
И наконец, в процессе воспитания и обучения у людей формируется чувство справедливости, которое может иметь эволюционное значение для общества в целом, а потому стать социальной нормой. Каким бы ни было происхождение этого чувства, именно им руководствуются предлагающие игроки, когда делают более щедрые предложения безотносительно к страху неприятия. Сьюзан Скит провела аудиторные эксперименты с разными ультимативными играми. Студенты, партнерами которых были их знакомые, вели себя заметно «справедливее» при дележе «пирога». Кроме того, некоторые студенты указывали культурные традиции в качестве причины поведения, не соответствующего теоретическим прогнозам.
Экспериментаторы попробовали несколько вариантов основной игры, чтобы провести различие между этими объяснениями. Проблему длительных отношений можно решить посредством более строгих процедур, в явном виде обеспечивающих анонимность. Само по себе это действие немного сказывается на результатах, но все так же не приводит к появлению настолько крайних предложений, как прогнозирует сугубо эгоистичный теоретический анализ методом обратных рассуждений. С оставшимися объяснениями (такими как страх неприятия и глубоко укоренившееся чувство справедливости) нам еще предстоит разобраться.
При рассмотрении так называемой диктаторской игры страх неприятия можно исключить. Ее участников снова разбивают на пары. Один игрок (скажем, игрок А) определяет способ разделения, а другой (Б) просто пассивно ждет, что соблаговолит ему выделить игрок А. Теперь разделение становится еще неравноценнее, но даже в этом случае большинство игроков А решают оставить себе не более 70%. Данный результат позволяет предположить, что здесь свою роль играет глубоко укоренившееся чувство справедливости.
Тем не менее такое чувство тоже имеет свои пределы. В ходе некоторых экспериментов чувство справедливости возникало даже при распределении ролей предлагающего и выбирающего в случайном порядке. В одном из вариантов игры участникам эксперимента давали простой тест, и тот, кто справился с ним лучше, получал роль предлагающего. Это вызывало у испытуемых ощущение, что они заслужили эту роль, и в итоге они чаще склонялись к более неравному разделению. Когда диктаторская игра проводилась с предоставлением заслуженных прав и введением более строгих условий анонимности, большинство игроков А оставляли себе все, но некоторые (около 5%) по-прежнему предлагали вариант 50 на 50.
Один из нас (Диксит) провел аудиторный эксперимент, в ходе которого группы по 20 студентов объединяли в один компьютерный кластер. Студентов случайным образом, при сохранении анонимности, разбивали по парам, а затем каждая пара пыталась договориться о распределении 100 баллов. Роли предлагающего и выбирающего не назначались; любой из пары мог сделать или принять предложение, причем в любой момент времени. Игроки, входящие в пару, могли обмениваться мгновенными сообщениями, которые выводились на экраны компьютеров. Раунд переговоров мог закончиться в любой произвольный момент в интервале от 3 до 5 минут; если к этому времени пара не достигала согласия, оба игрока получали ноль баллов. За весь период игры проводилось 10 подобных раундов с разными случайно выбранными соперниками, что устраняло вероятность сотрудничества посредством повторения. Студенты, участвовавшие в эксперименте, поддерживали постоянные отношения вне игры, но, как правило, не знали и не догадывались о том, с кем именно играют в каждом раунде, хотя в ходе эксперимента не предпринималось особых усилий для соблюдения анонимности. Оценка каждого студента за всю игру представляла собой сумму очков, набранных за 10 раундов. Ставки были довольно высокими, поскольку на эту оценку приходилось 5% от итоговой оценки за курс обучения!
Максимальное количество баллов, набранных в ходе игры, составило 515. Студенты, которые быстро согласились на разделение по принципу 50 на 50, получили самые высокие результаты. Те, кто пытался добиться гораздо более неравного распределения баллов или отказался разделить разницу в 10 баллов между разными предложениями и столкнулся с временным ограничением, получили низкие результаты. Создается впечатление, что умеренность и справедливость действительно вознаграждаются, даже если оцениваются в категориях собственного выигрыша.
5. Чередующиеся предложения, модель II: нетерпение
Теперь рассмотрим тип издержек в связи с промедлением в достижении соглашения. Предположим, фактический денежный эквивалент общей величины, подлежащей разделению, не уменьшается, но поскольку деньги имеют для игроков так называемую временную стоимость, они предпочитают раннее достижение соглашения позднему. Игроки делают предложения по очереди (так, как описано в ), но их временные предпочтения таковы, что деньги, полученные сейчас, лучше денег, полученных в будущем.
Для конкретности будем считать, что, по мнению обоих переговорщиков, 95 центов немедленно так же хороши, как и 1 доллар в следующем раунде.
Игрок, предпочитающий что-то прямо сейчас, а не в будущем, нетерпелив и придает меньшее значение будущему по сравнению с настоящим. Мы сталкивались с этой идеей в и обнаружили две причины существования данного феномена. Во-первых, у игрока А может быть возможность инвестировать свои деньги (скажем, 1 доллар) сейчас и получить основную сумму плюс проценты и прирост капитала по ставке r, в сумме (1 + r), в следующем периоде (завтра, на следующей неделе, в следующем году или независимо от продолжительности периода). Во-вторых, может иметься определенный риск того, что игра закончится между текущим моментом и следующим предложением (как в случае внезапного завершения игры в любой момент времени в интервале от 3 до 5 минут в описанном выше аудиторном эксперименте). Если p — вероятность того, что игра продолжится, то у шанса получить 1 доллар в следующем периоде в текущий момент ожидаемая ценность равна всего лишь p.
Рассмотрим переговорный процесс между двумя игроками с нулевыми значениями BATNA. Начнем с того, что один из них (скажем, игрок А) делает предложение о разделении 1 доллара. Если другой (игрок Б) отклонит его, то у него появится возможность сделать свое предложение в следующем раунде. Оба игрока находятся в одинаковом положении, когда каждый делает предложение, поскольку подлежащая разделению сумма всегда равна 1 доллару. Таким образом, в случае равновесия сумма (назовем ее x), которая достается игроку, делающему предложение в текущий момент, одна и та же, независимо от того, кто именно вносит предложение, А или Б. С помощью метода обратных рассуждений найдем уравнение, которое можно решить относительно x.
Предположим, игрок А начинает процесс чередования предложений. Он знает, что игрок Б может получить x в следующем раунде, когда наступит его очередь делать предложение. Поэтому игрок А должен выделить игроку Б сумму, которая как минимум эквивалентна (с точки зрения игрока Б) получению x в следующем раунде; другими словами, сейчас игрок А должен предложить игроку Б минимум 0,95x. (Не забывайте, что для игрока Б 95 центов немедленно эквивалентны 1 доллару в следующем раунде; значит, 0,95x сейчас — так же хорошо, как и x в следующем раунде.) Игрок А не выделит игроку Б больше, чем требуется для того, чтобы склонить игрока Б принять предложение. В итоге игрок А предлагает игроку Б ровно 0,95x, а себе оставляет (1 – 0,95x). Но сумма, получаемая игроком А в момент, когда он делает предложение, равна тому, что мы обозначили как x. Стало быть, x = 1 – 0,95x, или (1 + 0,95)x = 1, или x = 1/1,95 = 0,512.
Следует обратить внимание на два аспекта этих вычислений. Во-первых, хотя процесс допускает неограниченную последовательность чередующихся и встречных предложений, в случае равновесия самое первое предложение, которое делает игрок А, будет принято и игра завершится. Поскольку время имеет свою ценность, этот исход эффективен. От издержек в связи с промедлением зависит, сколько игрок А должен предложить игроку Б, чтобы добиться его согласия, а значит, это также влияет на обратные рассуждения игрока А. Во-вторых, игрок, который делает предложение первым, получит больше половины «пирога», а именно 0,512, а не 0,488. Стало быть, каждый игрок получает больше, когда первое предложение делает именно он, а не соперник. Но это преимущество гораздо меньше, чем в ультимативной игре, в которой нет будущих раундов со встречными предложениями.
Теперь предположим, что оба игрока не в равной степени терпеливы (или нетерпеливы, в зависимости от обстоятельств). Игрок Б по-прежнему считает, что 1 доллар в следующем раунде эквивалентен 95 центам сейчас, а игрок А приравнивает 1 доллар в следующем раунде к 90 центам в настоящий момент. Следовательно, игрок А готов принять меньшую сумму, чтобы получить ее быстрее, то есть он более нетерпелив. Такое неравенство уровней нетерпения может привести к неравным выигрышам от переговорного процесса в случае равновесия. Для того чтобы найти равновесие в данном примере, обозначим символом x сумму, которую получит игрок А, если он начинает процесс, и символом y сумму, которую получит игрок Б, если процесс начнет он.
Игрок А знает, что должен выделить игроку Б минимум 0,95y, иначе Б отклонит предложение в пользу суммы y, которую, как ему известно, он сможет получить, когда наступит его очередь делать предложение. Таким образом, сумма x, которую получит игрок А, должна равняться 1 – 0,95y, то есть x = 1 – 0,95y. Аналогичным образом, когда процесс начинает игрок Б, он знает, что должен выделить игроку А минимум 0,90x и тогда y = 1 – 0,90x. Эти два уравнения можно решить относительно x и y:
x = 1 – 0,95(1 – 0,9x),
[1 – 0,95(0,9)]x = 1 – 0,95,
0,145x = 0,05,
x = 0,345.
y = 1 – 0,9(1 – 0,95y),
[1 – 0,9(0,95)]y = 1 – 0,9,
0,145y = 0,10,
y = 0,690.
Обратите внимание, что сумма x и y не равна 1, поскольку каждая из этих величин представляет собой выигрыш соответствующего игрока при условии, что он делает предложение первым. Таким образом, когда первое предложение делает игрок А, он получает 0,345, а игрок Б 0,655; когда первое предложение делает Б, он получает 0,69, а игрок А 0,31. Опять же, каждый игрок получает более высокий результат, когда именно он делает первое предложение, и снова разница незначительна.
Исход варианта игры с разными уровнями нетерпения существенно отличается от исхода предыдущей игры с одинаковыми уровнями нетерпения. При разных уровнях нетерпения более нетерпеливый игрок А получает намного меньше, чем игрок Б, даже тогда, когда у него есть возможность сделать первое предложение. Мы предполагали, что игрок, соглашающийся на меньшую сумму, чтобы получить ее быстрее, получит в итоге меньше, но разница действительно впечатляющая. Соотношение долей игрока А и Б составляет почти 1 к 2.
Как обычно, теперь на основании этих примеров запишем обобщенные выводы в алгебраическом виде. Допустим, игрок А рассматривает 1 доллар сейчас как эквивалент (1 + r) долларов, полученных на одно предложение позже, или, что то же самое, 1/(1 + r) долларов сейчас как эквивалент 1 доллара на одно предложение позже. Для краткости будем использовать в расчетах a вместо 1/(1 + r). Аналогичным образом предположим, что игрок Б рассматривает 1 доллар сейчас как эквивалент (1 + s) долларов, полученных на одно предложение позже; будем использовать в расчетах b вместо 1/(1 + s). Если значение r высокое (или, что то же самое, а низкое), значит, игрок А весьма нетерпелив. Точно так же, игрок Б нетерпелив, если значение s высокое (или b низкое).
Мы анализируем переговоры, проходящие в виде чередующихся раундов, с общей суммой 1 доллар, которую нужно разделить между двумя игроками с нулевыми значениями BATNA. (Как только вы поймете этот случай, то без труда сможете проанализировать и более общий случай.) Каким будет равновесие обратных рассуждений в этой игре?
Мы можем найти выигрыши в таком равновесии, расширив представленное выше простое доказательство. Допустим, выигрыш игрока А в равновесии обратных рассуждений равен x, если он делает предложение первым, а игрока Б — y, когда первое предложение вносит он. Мы найдем пару уравнений, связывающих значения x и y, а затем решим их, чтобы определить равновесные выигрыши.
Когда игрок А делает предложение, он знает, что должен выделить игроку Б сумму, которую тот считает эквивалентной y в следующем периоде. Эта сумма составляет by = y/(1 + s). После предложения игроку Б игрок А может получить только то, что осталось: x = 1 – by.
Точно так же, когда игрок Б делает предложение, он должен выделить игроку А эквивалент x в следующем периоде, а именно ax. Значит, y = 1 – ax. Теперь решить эти уравнения легче. Мы имеем x = 1 – b(1 – ax), или (1 – ab)x = 1 – b. Если выразить это уравнение через r и s, оно будет выглядеть так:
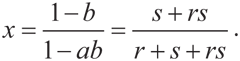
Аналогичным образом y = 1 – a(1 – by), или (1 – ab)y = 1 – a. Тогда уравнение примет такой вид:
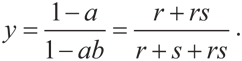
Хотя это быстрое решение может показаться ловким трюком, оно получено в соответствии с теми же действиями, что и используемые ранее; кроме того, немного ниже мы приведем другую аргументацию, дающую точно такой же ответ. Но сначала проанализируем некоторые свойства этого ответа.
Прежде всего обратите внимание, что, как и в примере с разными уровнями терпения, сумма величин x и y больше 1:
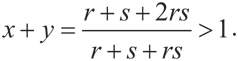
Помните, что x — это то, что получает игрок А, когда он вправе сделать первое предложение, а y — то, что в аналогичном случае получает игрок Б. Когда игрок А делает предложение первым, игрок Б получает (1 – x), что меньше y; это подтверждает преимущество игрока А в случае, если он делает первое предложение. Точно так же, когда игрок Б делает предложение первым, он получает y, а игрок А (1 – y), что меньше x.
Однако r и s — как правило, небольшие числа. Когда предложения могут быть сделаны с короткими промежутками, скажем, через неделю, или один день, или один час, процент, который может быть начислен на ваши деньги за период между ними, или вероятность того, что игра закончится именно на протяжении следующего промежутка, достаточно мала. Например, если r равно 1% (0,01), а s — 2% (0,02), то формулы дают x = 0,668 и y = 0,337, а значит, преимущество от права сделать первое предложение составляет всего 0,005. (Игрок А получает 0,668, когда он сам делает первое предложение, но 1 – 0,337 = 0,663, когда его делает игрок Б; разница — 0,005.) Строго говоря, когда r и s — небольшие числа по сравнению с 1, то их произведение rs на самом деле очень мало; следовательно, мы можем исключить rs из формулы приближенного решения задачи разделения, не зависящей от того, какой игрок делает первое предложение:
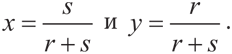
Теперь x + y примерно равно 1.
Важно то, что в приближенном решении x и y — это доли излишка, которые достаются двум игрокам, а y/x = r/s; другими словами, доли игроков обратно пропорциональны их степени нетерпения, выраженной в виде r и s. Если игрок Б в два раза нетерпеливее игрока А, то игрок А получит в два раза больше, чем игрок Б; значит, их доли составляют 1/3 и 2/3, или 0,333 и 0,667 соответственно. Таким образом, мы видим, что терпение — важное преимущество в переговорах. Наш формальный анализ подтверждает интуитивный вывод о том, что, если вы очень нетерпеливы, другой игрок может предложить вам быструю, но невыгодную сделку, зная, что вы на нее согласитесь.
Эффект нетерпения вредит США, нашим органам власти и дипломатам на многих переговорах с другими странами. Американский политический процесс придает большое значение скорости. Средства массовой информации, заинтересованные группы и конкурирующие политики требуют немедленных результатов и охотно критикуют администрацию или дипломатов за любое промедление. При таком давлении переговорщики всегда испытывают искушение вернуться хотя бы с каким-то решением. Но зачастую эти результаты оставляют желать лучшего в долгосрочной перспективе; уступки других стран содержат различные уловки, а их обещания далеко не достоверны. Правительство США преподносит такие сделки как большую победу, но через несколько лет они, как правило, расторгаются. Финансовый кризис 2008 года — еще один весьма драматичный пример. Когда произошел крах рынка недвижимости, ряд крупных финансовых учреждений, активы которых были обеспечены ипотечными кредитами, очутились на грани банкротства. Это привело к сокращению размера кредитования, что, в свою очередь, поставило экономику США под угрозу глубокого спада. Кризис разразился в сентябре, в разгар президентской кампании. Министерство финансов, Федеральная резервная система и политические лидеры в Конгрессе стремились действовать быстро. Это нетерпение привело к предложению многим финансовым учреждениям гораздо более щедрых условий спасения, тогда как более медленный процесс обеспечил бы налогоплательщикам менее болезненный результат и открыл бы перед ними гораздо более приемлемые перспективы участия в будущих прибылях на спасенные активы.
Когда люди, потерпевшие убытки, ведут со страховой компанией переговоры о страховом покрытии, их позиция намного слабее. Часто компании предлагают тем, кто понес серьезный ущерб, заниженную сумму страхового возмещения, зная, что им необходимо немедленно начать все сначала, а значит, у них высокая степень нетерпения.
На концептуальном уровне формула y/x = r/s связывает подход к переговорам, основанный на некооперативной игре, с кооперативным подходом решения Нэша, о котором говорилось в . Выведенная в этом разделе формула для определения долей имеющегося излишка при нулевых значениях BATNA принимает вид y/x = k/h. При кооперативном подходе соотношение между долями двух игроков было таким же, как и соотношение между силой их переговорных позиций, однако предполагалось, что показатели этой силы каким-то образом получены извне. Теперь мы можем объяснить силу переговорных позиций с точки зрения базовых характеристик игроков: значения h и k обратно пропорциональны уровням нетерпения игроков r и s. Иными словами, кооперативному решению Нэша можно дать альтернативную и, возможно, более приемлемую интерпретацию как равновесию обратных рассуждений в некооперативной игре с взаимными предложениями, если мы представим абстрактные показатели силы переговорных позиций в кооперативном решении в виде присущих игрокам характеристик, таких как нетерпение.
И наконец, обратите внимание, что в данном случае соглашение снова может быть достигнуто немедленно, так как самое первое предложение принимается. Как всегда, полный анализ методом обратных рассуждений носит дисциплинирующий характер, поскольку игрок, делающий предложение первым, осознает достоверность того, что другой игрок отклонит менее приемлемый вариант.
В заключение раздела предлагаем альтернативный способ получения той же (точной) формулы равновесных предложений, которую мы вывели ранее. Допустим, игра состоит из 100 раундов; игрок А делает первое предложение, а игрок Б — последнее. Начнем процесс обратных рассуждений с раунда 100: игрок Б оставит себе весь доллар. Следовательно, в раунде 99 игрок А должен предложить игроку Б эквивалент 1 доллара в раунде 100, а именно b; игроку А останется (1 – b). Далее будем выполнять такой же анализ в обратном порядке.
В раунде 98 игрок Б предлагает игроку А a(1 – b) и оставляет себе
1 – a(1 – b) = 1 – a + ab.
В раунде 97 игрок А предлагает игроку Б b(1 – a + ab) и оставляет себе
1 – b(1 – a + ab) = 1 – b + ab – ab2.
В раунде 96 игрок Б предлагает игроку А a(1 – b + ab – ab2) и оставляет себе
1 – a + ab – a2b + a2b2.
В раунде 95 игрок А предлагает игроку Б b(1 – a + ab – a2b + a2b2) и оставляет себе
1 – b + ab – ab2 + a2b2 + a2b3.
Продолжив анализ по такой схеме, мы увидим, что в раунде 1 игрок А оставит себе долю
1 – b + ab – ab2 + a2b2 – a2b3 + … + a49b49 – a49b50 = (1 – b)[1 + ab + (ab)2 + … + (ab)49].
Последствия увеличения количества раундов очевидны. Мы просто будем получать все больше членов этого ряда, возрастающих в геометрической прогрессии в ab раз на каждых два предложения. Для того чтобы определить выигрыш игрока А в случае, когда он делает первое предложение в бесконечно большой последовательности взаимных предложений, необходимо найти предел бесконечной геометрической прогрессии. В показано, как находить сумму таких рядов. Воспользовавшись представленной там формулой, имеем
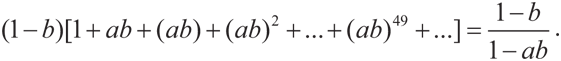
Это и есть то же решение для x, что и полученное выше. Путем аналогичных рассуждений вы сможете определить выигрыш игрока Б, когда он делает первое предложение, что позволит вам улучшить понимание материала и навыки вычислений.
6. Манипулирование информацией в процессе переговоров
Мы видели, что результат переговоров в значительной мере зависит от различных характеристик сторон, самые важные из которых — показатели BATNA и уровни нетерпения переговорщиков. До сих пор мы исходили из предположения, что игроки знают характеристики друг друга так же хорошо, как свои собственные. На самом деле мы полагали, что каждый игрок знает то, что известно другому, и т. д.; иначе говоря, что характеристики игроков — это их общее знание. В действительности мы часто ведем переговоры, не зная BATNA или уровня нетерпения другой стороны, а иногда мы не знаем точного значения даже собственного BATNA.
Как мы видели в , игра с подобной неопределенностью или информационной асимметричностью сопровождается использованием стратегий сигнализирования и скрининга в целях манипулирования информацией. Переговоры изобилуют такими стратегиями. Игрок с хорошим показателем BATNA или высоким уровнем терпения стремится сигнализировать об этом другому игроку. Однако в связи с тем, что игроки часто пытаются имитировать столь выигрышные характеристики, другая сторона скептически отнесется к подобным сигналам и будет тщательно их проверять на предмет достоверности. Кроме того, каждая сторона попытается применить скрининг, воспользовавшись стратегиями, побуждающими другую сторону предпринять действия, раскрывающие ее истинные характеристики.
В данном разделе мы проанализируем некоторые стратегии, применяемые покупателями и продавцами на рынке недвижимости. Большинство американцев проявляют активность на рынке жилья несколько раз в жизни, но у профессиональных агентов или брокеров по операциям с недвижимостью гораздо более обширный опыт в данной области. Более того, рынок недвижимости — один из немногих в США, на котором приемлем и даже приветствуется торг и переговоры по поводу цены, поэтому в нашем распоряжении немалый опыт стратегий в этой сфере. Мы будем опираться на него во многих примерах и интерпретируем в свете концепций и выводов теории игр.
Когда вы задумываетесь о покупке дома в новом районе, вам вряд ли известен общий диапазон цен на дома интересующего вас типа. Поэтому для начала вы должны выяснить этот диапазон и определить свой показатель BATNA. Это вовсе не означает, что вы должны ознакомиться с объявлениями в газетах или со списками выставленных на продажу домов, составленными агентствами по недвижимости. В местных газетах и на некоторых сайтах публикуется информация о последних реальных операциях с недвижимостью и фактические цены; вам нужно сравнить их с ценами, запрашиваемыми продавцами этих домов, что позволит составить представление о состоянии рынка и возможном диапазоне торга.
Далее следует определить (посредством скрининга) BATNA и уровень нетерпения другой стороны. Если вы покупатель, вам необходимо выяснить, почему дом продается и как давно он выставлен на продажу. Если дом пустует, то почему и какой период? Если владельцы дома разводятся или переехали в другое место и оплачивают новое жилье за счет промежуточного кредита, скорее всего, у них низкий показатель BATNA или высокий уровень нетерпения.
Кроме того, вы должны выяснить соответствующие аспекты предпочтений другой стороны, даже если эти предпочтения покажутся вам иррациональными. Например, некоторые люди считают предложение гораздо ниже запрашиваемой цены оскорблением, поэтому ни на каких условиях не станут продавать дом тому, кто предложит такую цену. Подобные нормы отличаются в разных регионах и в разное время. Имеет смысл выяснить, какова общепринятая практика в этой области.
Важно то, что принятие предложения раскрывает более точную информацию об истинной готовности игрока платить, чем любые другие методы, а значит, другой игрок может использовать это свойство с выгодой для себя. Один наш друг, блестящий специалист по теории игр, попытался применить такую уловку. Он торговался по поводу цены торшера. Продавец запросил 100 долларов, и переговоры дошли до того момента, когда наш друг предложил купить торшер за 60 долларов. Продавец согласился, и тут наш друг подумал: «Этот парень готов продать торшер за 60 долларов, значит, его истинная минимальная цена еще ниже. Попробую-ка я выяснить, так ли это». И наш друг сказал: «А как насчет 55 долларов?» Продавец очень расстроился, отказался продавать торшер по любой цене и попросил нашего друга покинуть магазин и больше никогда не возвращаться.
Поведение продавца подтвердило тот факт, что в переговорах совершенно неприемлемо отказываться от предложения после того, как оно было принято. Такая норма имеет смысл в контексте всех переговорных игр, которые ведутся в обществе. Если другой игрок не может по доброй воле принять обсуждаемое предложение без опасений повторения ситуации, как произошедшая с нашим другом, то каждый переговорщик будет ждать, когда другой примет предложение, и весь процесс переговоров застопорится. Стало быть, такое поведение должно быть неприемлемым. Общество может этого добиться, сделав надлежащее поведение социальной нормой, которой люди придерживаются на подсознательном уровне, как это сделал продавец в нашем примере.
В предложении может быть точно указано, что оно открыто на протяжении некоего ограниченного периода; эта оговорка может быть частью самого предложения. В предложениях о работе обычно указывается крайний срок, к которому необходимо дать ответ; магазины объявляют распродажу на ограниченный период. Однако в этом случае предложение должно представлять собой настоящий пакет таких условий, как цена и сроки, и нарушение любого из них провоцирует закономерный подсознательный гнев. Например, покупатели очень недовольны, когда, придя в магазин в период распродажи, не находят заявленного в рекламе товара. Магазин должен предложить купон на отсутствующий товар, чтобы клиент мог его купить со скидкой, когда он появится в продаже по обычной цене. Но даже такое предложение создает для покупателей определенные неудобства, поэтому магазин рискует потерять их расположение. В рекламном объявлении о распродаже магазин должен четко указать: «количество товаров ограниченно, купоны на скидки не предоставляются», но даже в этом случае многие покупатели выказывают недовольство, если товар заканчивается.
Следующий пункт в нашем списке стратегий, которые целесообразно использовать в переговорах один на один (как на рынке недвижимости), — сигнализирование о высоком показателе BATNA или высоком уровне терпения. Лучший способ подать сигнал о терпении — быть терпеливым. Не делайте встречных предложений слишком быстро, «пусть продавцы думают, что они вас потеряли». Такой сигнал достоверен, поскольку для человека, которому терпение не свойственно, имитация неторопливого подхода слишком обременительна. Кроме того, вы можете также подать сигнал о высоком показателе BATNA, делая вид, что уходите, — распространенная тактика на базарах в других странах, а также на блошиных рынках и гаражных распродажах в Соединенных Штатах.
Даже если у вас низкий BATNA, вы можете взять на себя обязательство не принимать предложение ниже определенного уровня. Такое ограничение действует так же, как и высокий показатель BATNA, поскольку другая сторона не может рассчитывать на то, что вы согласитесь на предложение ниже этого уровня. В контексте операций с недвижимостью вы можете заявить, что у вас нет возможности платить более высокую цену, сославшись на (вымышленного) прижимистого отца, который оплачивает первый взнос, или на жену, которой на самом деле дом не нравится, поэтому она не позволит вам заплатить за него ни на цент больше. Продавцы могут применить аналогичную тактику. В переговорах о повышении заработной платы в качестве такого метода выступает мандат. Проводится профсоюзное собрание, на котором принимается резолюция (мандат), наделяющая руководителей профсоюза полномочиями представлять интересы работников на переговорах, но с оговоркой, что переговорщики не должны принимать предложение ниже определенного уровня, указанного в резолюции. Тогда на встрече с руководством компании профсоюзные лидеры могут сказать, что у них связаны руки и нет времени возвращаться к членам профсоюза за разрешением на любое более низкое предложение.
Большинство этих стратегий сопряжены с определенным риском. В то время как вы подаете сигнал о своем терпении посредством ожидания, продавец дома может найти другого заинтересованного покупателя. Пока работодатель и профсоюз ждут уступок с каждой стороны, напряженность может повыситься до такого уровня, что забастовка, которая дорого обойдется обеим сторонам, станет неизбежной. Другими словами, многие стратегии манипулирования информацией — примеры балансирования на грани. В мы видели, как в таких играх может наступить неблагоприятный для обеих сторон исход. То же самое можно сказать и о переговорах. Угрозы о прекращении переговоров или начале забастовки — это стратегические ходы, нацеленные на более быстрое достижение соглашения или заключение более выгодной сделки для игрока, делающего такой ход. В то же время фактический срыв переговоров или начало забастовки — это пример угрозы, которая «пошла не так». Игрок, выдвигающий угрозу (инициирующий балансирование на грани), должен оценить риск и потенциальную выгоду, прежде чем принимать решение о том, становиться ли он на этот путь и насколько далеко можно по нему зайти.
7. Переговоры с участием многих сторон и переговоры по многим вопросам
До сих пор наше обсуждение ограничивалось классической ситуацией, в которой две стороны договариваются о распределении определенного общего излишка. Однако в реальной жизни многие переговоры включают в себя несколько сторон или несколько вопросов одновременно. Хотя такие игры становятся более сложными, зачастую увеличение количества переговорщиков или рассматриваемых тем облегчает процесс достижения взаимовыгодного соглашения. В данном разделе мы кратко рассмотрим эти вопросы.
А. Переговоры по многим вопросам
В каком-то смысле мы уже рассматривали такие переговоры. Переговоры о цене между продавцом и покупателем всегда включают в себя два пункта: 1) объект, который предлагается на продажу или рассматривается на предмет покупки; 2) деньги. Возможность получения взаимной выгоды появляется в случае, когда ценность такого объекта для покупателя выше, чем для продавца, то есть когда покупатель готов отдать за данный объект больше денег, чем продавец готов принять. В таком случае соглашение, достигнутое в ходе переговоров, выгодно обеим сторонам.
Этот принцип применим и в более общем случае. Международная торговля — классический пример. Рассмотрим две гипотетические страны, Фридонию и Илирию. Если Фридония может производить вместо 1 буханки хлеба 2 бутылки вина (используя меньше ресурсов, таких как труд и земля, в процессе выпечки хлеба и направив их на производство большего количества вина), а Илирия может выпускать вместо 1 бутылки вина 1 буханку хлеба (перераспределяя ресурсы в обратном направлении), то вместе они могут произвести больше продукции «из ничего». Предположим, Фридония может выпустить на 200 бутылок вина больше, если выпечет на 100 буханок хлеба меньше, а Илирия может выпечь на 150 буханок хлеба больше, если выпустит на 150 бутылок вина меньше. Такое перераспределение ресурсов позволит этим странам произвести на 50 буханок хлеба и 50 бутылок вина больше, чем они выпускали изначально. Эти хлеб и вино и есть тот «излишек», который обе страны могут создать, если договорятся о том, как его разделить между собой. Допустим, Фридония отдаст Илирии 175 бутылок вина и получит взамен 125 буханок хлеба. Тогда у каждой страны будет на 25 буханок хлеба и 25 бутылок вина больше, чем раньше. Но существует целый диапазон вариантов обмена, соответствующих разным способам разделения выгоды. Один крайний вариант состоит в том, что Фридония может отдать все 200 дополнительных бутылок вина в обмен на 101 буханку хлеба от Илирии; в итоге почти вся выгода от сделки достанется Илирии. С другой стороны, Фридония может отдать только 151 бутылку вина в обмен на 150 буханок хлеба Илирии, и тогда Фридония получит почти всю выгоду от сделки. Между этими двумя крайними вариантами находится область, в рамках которой обе страны могут вести переговоры о разделении выгоды от обмена продукцией.
Общий принцип понятен. Когда во время переговоров одновременно обсуждаются два или более вопроса и две стороны готовы обменять большее количество чего-то одного на меньшее количество другого в разных пропорциях, то они могут заключить взаимовыгодную сделку. Взаимная выгода может обеспечиваться посредством обмена в соотношении, находящемся примерно посредине между разными уровнями готовности двух сторон к обмену. Разделение выгоды зависит от выбора соотношения, в котором будет осуществляться обмен. Чем оно ближе к уровню готовности одной стороны к обмену, тем меньшую выгоду она получит от данной сделки.
Теперь вы видите, как можно расширить возможности для заключения взаимовыгодной сделки путем одновременного рассмотрения большего количества вопросов. При этом повышается вероятность обнаружить расхождения между соотношениями оценок двух сторон, а значит, появляется больше перспектив для взаимной выгоды. Например, в ситуации с домом многие приборы и предметы мебели могут не пригодиться продавцу в новом доме, но зато могут устраивать покупателя и соответствовать его вкусу, а значит, представлять для него ценность. В таком случае, если продавца не удастся уговорить снизить цену, он может хотя бы согласиться включить эти предметы в исходную цену ради заключения сделки.
Тем не менее увеличение количества обсуждаемых вопросов имеет свои минусы. Если для вас что-то представляет большую ценность, вы можете побояться выносить этот вопрос за стол переговоров. Вас может беспокоить, что другая сторона добьется от вас значительных уступок, зная о вашем желании защитить столь ценный для вас предмет переговоров. В худшем случае новая тема обсуждения в ходе переговоров может обеспечить одной стороне возможность применить угрозу, которая снизит BATNA другой стороны. Например, страна, ведущая дипломатические переговоры, может оказаться в уязвимом положении в результате введения экономического эмбарго, поэтому она предпочла бы рассматривать политические и экономические вопросы по отдельности.
Б. Переговоры с участием многих сторон
Переговоры с одновременным участием нескольких сторон также могут способствовать достижению соглашения, поскольку вместо заключения двусторонних сделок переговорщики могут найти круг взаимных уступок. В этой ситуации международная торговля — самый показательный пример. Предположим, Соединенные Штаты эффективно выращивают пшеницу, но менее продуктивны в производстве автомобилей; у Японии высококачественные автомобили, но нет нефти, а у Саудовской Аравии много нефти, но нет возможности выращивать пшеницу. Ведя переговоры попарно, эти страны достигли бы гораздо меньшего, а вместе могут заключить взаимовыгодную сделку.
Как и переговоры по многим вопросам, переговоры с участием нескольких сторон несут определенные риски. Скажем, в нашем примере сделка сводилась бы к следующему: США отправляют оговоренное количество пшеницы в Саудовскую Аравию, та предоставляет оговоренный объем нефти Японии, та, в свою очередь, отправляет соответствующее количество автомобилей Соединенным Штатам. Но представим, что Япония не выполнит свою часть договора. Саудовская Аравия не может принять мер против Соединенных Штатов, поскольку она не предлагает им ничего, что могла бы не предоставлять. Единственное, что может сделать Саудовская Аравия, — это нарушить условия сделки и не отправлять нефть в Японию. Следовательно, гарантировать выполнение многостороннего соглашения весьма проблематично. Генеральное соглашение по тарифам и торговле в период с 1946 по 1994 год, а в дальнейшем Всемирная торговая организация действительно столкнулись с большими трудностями в отношении выполнения соглашений и наложения взысканий на страны, нарушающие установленные правила.
Резюме
Переговоры сводятся к попыткам разделить их сторонами излишек (избыточную стоимость), который они могут получить при условии достижения соглашения. Переговоры можно представить как кооперативную игру, в которой стороны совместно находят и реализуют решение, либо как (структурированную) некооперативную игру, в которой стороны выбирают стратегии по отдельности и пытаются достичь равновесия.
Кооперативное решение Нэша основано на трех принципах: инвариантность исходов к линейным изменениям размера выигрышей, эффективность и инвариантность к исключению посторонних альтернатив. Это решение представляет собой правило, определяющее соотношение разделения излишка, превышающего уровни страховочных выигрышей каждой стороны (обозначаемые также термином лучшая альтернатива обсуждаемому соглашению, BATNA), в соответствии с силой переговорных позиций сторон. Стратегические манипуляции со страховочными выигрышами могут использоваться для повышения выигрыша одной из сторон.
В некооперативной среде с чередующимися и встречными предложениями для поиска равновесия используется анализ методом обратных рассуждений, как правило, приводящих к принятию предложения, сделанного в первом раунде. Если стоимость излишка с каждым отказом убывает, сумма (гипотетических) его долей, потерянных из-за отказов одного игрока, представляет собой выигрыш другого игрока в случае равновесия. Если отсрочка соглашения сопряжена с большими издержками из-за нетерпения, равновесное предложение подразумевает разделение излишка обратно пропорционально уровням нетерпения сторон. Экспериментальные данные свидетельствуют, что для достижения соглашения в таких играх их участники часто предлагают больше, чем необходимо; считается, что подобное поведение связано с анонимностью игроков и их представлениями о справедливости.
В переговорных играх с асимметричной информацией большую роль играют сигнализирование и скрининг. Одни стороны стремятся сообщить о высоком уровне BATNA или величайшем терпении, другим необходимо применить скрининг для получения правдивой информации о наличии этих характеристик. В переговорах по многим вопросам или со многими участниками порой легче достичь соглашения, но при этом они сопряжены с более высоким уровнем риска или трудностями с обеспечением выполнения условий соглашений.
Ключевые термины
Излишек
Кооперативное решение Нэша
Лучшая альтернатива соглашению, BATNA
Нетерпение
Переговоры с переменной угрозой
Убывание излишка
Ультимативная игра
Чередующиеся предложения
Эффективная граница
Эффективный исход
Упражнения с решениями
S1. Рассмотрим ситуацию с переговорами между Compaq Computer Corporation и калифорнийским бизнесменом, которому принадлежал домен . Компания Compaq, недавно поглотившая Digital Equipment Corporation, хотела использовать веб-адрес этого бизнесмена для поисковой системы Digital, у которой был тогда адрес . Судя по всему, летом 1998 года между Compaq и бизнесменом велись долгие и трудные переговоры о цене продажи этого домена.
Хотя бизнесмен был «более мелким» участником игры, окончательное соглашение подразумевало продажу домена по цене 3,35 миллиона долларов. В августе компания Compaq подтвердила его покупку, а в сентябре начала его использовать, но отказалась сообщать финансовые подробности сделки. С учетом этой информации выскажите свое мнение о возможных значениях BATNA двух игроков, силе их переговорных позиций и уровне нетерпения, и был ли достигнут кооперативный исход в этой игре.
S2. Али и Баба делят общую сумму, которая стартует с сотни долларов. Али делает первое предложение, в котором оговорено, как будут разделены 100 долларов. Если Баба его примет, игра завершится. Если отклонит, общая сумма сократится на 1 доллар и составит 99 долларов. И дальше Баба делает предложение. Так они поочередно делают предложения, и каждый раз, когда предложение отклоняется, из общей суммы вычитается один доллар. BATNA Али составляет 2,25 доллара, а BATNA Бабы — 3,50 доллара. Найдите равновесие обратных рассуждений в этой игре.
S3. Две гипотетические страны Эуфория и Милишия ведут переговоры об урегулировании конфликта. Их представители встречаются раз в месяц, начиная с января, и по очереди делают предложения. Допустим, общая сумма выигрыша от достижения соглашения составляет 100 баллов. В ноябре правительству Эуфории предстоят перевыборы. Если на октябрьской встрече оно не добьется заключения договора, то проиграет выборы, что для него так же плохо, как и получить от соглашения ноль баллов. Правительство Милишии абсолютно не интересует исход соглашения; оно может продолжить переговоры или даже начать воевать, поскольку его устроит любой выигрыш, даже намного меньше 100 баллов.
a) Каким будет исход переговоров? Как он зависит от того, кто сделает первый ход?
b) С учетом ответа, полученного в пункте а, объясните, почему реальные переговоры часто ведутся вплоть до крайнего срока.
Упражнения без решений
U1. Вспомните вариант игры в установление цены на пиццу из , в котором один ресторан (ресторан Донны Deep Dish) был гораздо больше другого (ресторан Пирса Pizza Pies). Таблица выигрышей этой игры выглядит так:

Некооперативное равновесие в доминирующих стратегиях («высокая цена» / «низкая цена») обеспечивает прибыль 132 пиццерии Донны и 70 пиццерии Пирса, что в сумме равно 202. Если бы владельцы обоих ресторанов могли достичь равновесия («высокая цена» /«высокая цена»), их общая прибыль составила бы 156 + 60 = 216, но Пирс не согласился бы на такую цену.
Предположим, рестораны могут достичь поддающегося принудительному выполнению соглашения, по условиям которого оба назначают высокую цену и Донна выплачивает Пирсу определенную сумму. Альтернатива такому соглашению — некооперативное равновесие в доминирующих стратегиях. Владельцы ресторанов ведут переговоры о заключении соглашения, причем переговорная позиция Донны в 2,5 раза сильнее, чем Пирса. Какую сумму выплатит Донна Пирсу по условиям соглашения, достигнутого в результате переговоров?
U2. Рассмотрим двух игроков, договаривающихся по поводу излишка, изначально равного целой величине V, посредством чередующихся предложений. Другими словами, игрок 1 делает предложение в первом раунде; если игрок 2 отклоняет его, он делает предложение во втором раунде; если игрок 1 отклоняет его, он делает предложение в третьем раунде и т. д. Предположим, на протяжении каждого периода имеющийся излишек уменьшается на постоянную величину c = 1. Например, если игроки достигают соглашения во втором раунде, они делят излишек V – 1, если в пятом раунде, то V – 4. Это означает, что игра закончится после V раундов, поскольку больше будет не о чем договариваться. (Для сравнения вспомните пример с билетом на футбол, в котором его стоимость для болельщика начиналась со 100 долларов и снижалась на 25 долларов за одну четверть в течение четырех четвертей матча.) В этой задаче сперва необходимо найти равновесие обратных рассуждений, а затем равновесие обобщенной версии этой игры, в которой два игрока могут иметь BATNA.
a) Начнем с простой версии. Найдите равновесие обратных рассуждений при V = 4. В каком периоде игроки достигнут соглашения? Какой выигрыш x получит игрок 1 и какой выигрыш достанется игроку 2?
b) Найдите равновесие обратных рассуждений при V = 5.
c) Найдите равновесие обратных рассуждений при V = 10.
d) Найдите равновесие обратных рассуждений при V = 11.
e) Теперь подготовьтесь обобщить результат. Каким будет равновесие обратных рассуждений при любом целом значении V? (Подсказка: вам нужно проанализировать четные и нечетные значения V по отдельности.)
Теперь рассмотрите BATNA. Представим, что к концу раунда V соглашение не достигнуто, игрок А получает выигрыш a, а игрок Б — выигрыш b. Предположим также, что a и b — целые числа, удовлетворяющие неравенству a + b < V, а значит, достигнув соглашения, игроки могут получить более высокие выигрыши, чем в противном случае.
f) Допустим, V = 4. Каким будет равновесие обратных рассуждений при любых возможных значениях a и b? (Подсказка: вам может понадобиться вывести более чем одну формулу, точно так же как в пункте e. Если вы не справитесь с этой задачей, попытайтесь сперва решить ее при конкретных значениях a и b, а затем измените их и посмотрите, что произойдет. Для того чтобы выполнить анализ методом обратных рассуждений, вам необходимо определить, на каком шаге значение V уменьшается до такого уровня, что соглашение больше не будет обеспечивать прибыль двум сторонам переговоров.)
g) Предположим, V = 5. Каким будет равновесие обратных рассуждений при любых возможных значениях a и b?
h) Каким будет равновесие обратных рассуждений при любых возможных значениях a, b и V?
i) Смягчите условие о том, что a, b и V — целые числа: пусть они будут неотрицательными, удовлетворяющими неравенству a + b < V. Также измените предположение, что значение V уменьшается на 1 каждый период: пусть оно уменьшается за каждый период на постоянную величину c > 0. Найдите равновесие обратных рассуждений в этой обобщенной задаче.
U3. Пусть x — сумма, которую просит игрок А, а y — сумма, которую просит игрок Б при первом предложении в переговорной игре с чередующимися предложениями при наличии нетерпения. Степень их нетерпения составляет r и s соответственно.
a) Если мы используем приближенные формулы x = s / (r + s) для x и y = r / (r + s) для y, а также если игрок Б в два раза нетерпеливее игрока А, то А получит две трети излишка, а Б — одну треть. Проверьте правильность этого результата.
b) Пусть r = 0,01, а s = 0,02. Сравните значения x и y, найденные с помощью метода аппроксимации, с более точными решениями для x и y, найденными посредством формул x = (s + rs)/(r + s+ rs) и y = (r + rs)/(r + s+ rs), выведенных в данной главе.

