10 Дилемма заключенных и повторяющиеся игры
В этой главе мы продолжим изучать широкий класс игр и остановимся на концепции «дилемма заключенных». Пожалуй, это классический пример теории стратегии и ее последствий для прогнозирования поведения участников игры, и большинство людей, изучающих теорию игр, с ним знакомы. Даже те, кто не имеет никаких знаний в данной области, наверняка наслышан об этой концепции или как минимум о ее существовании. Дилемма заключенных — это игра, в которой у каждого игрока есть доминирующая стратегия, но равновесие, возникающее в результате применения всеми игроками своих доминирующих стратегий, обеспечивает каждому из них худший исход, чем при использовании доминируемых стратегий. Парадоксальность этого равновесия поднимает ряд более сложных вопросов о характере взаимодействия участников игры, ответить на которые можно только посредством тщательного анализа. Цель данной главы — предоставить вам дополнительные инструменты такого анализа.
В мы уже сталкивались с дилеммой заключенных. Там же мы обратили внимание на любопытную природу равновесия, которое на самом деле «плохой» исход для игроков. «Заключенные» могут найти другой исход, более предпочтительный равновесному, но у них возникают трудности с выполнением этой задачи. В данной главе мы рассмотрим вероятность достижения такого исхода. Иными словами, проанализируем, могут ли (и каким образом) участники игры «дилемма заключенных» достичь и сохранить взаимовыгодный кооперативный исход, преодолев свою естественную заинтересованность в отказе от сотрудничества ради личной выгоды. Сначала разберем стандартную игру «дилемма заключенных», а затем сформулируем три категории решений. Первый и самый важный метод решения таких игр сводится к повторению стандартной однократной игры. Именно за разработку общей теории повторяющихся игр Роберт Ауманн (вместе с Томасом Шеллингом) в 2005 году получил Нобелевскую премию по экономике. Как обычно, на вводном этапе мы приведем несколько простых примеров этой общей теории, а затем проанализируем еще две категории возможных решений, в основе которых лежат схемы взыскания (или вознаграждения) и роль лидерства.
Глава заканчивается обзором некоторых экспериментальных данных, касающихся дилеммы заключенных, а также описанием примеров реальных дилемм в действии. Как правило, в ходе таких экспериментов игроки участвуют в различных вариантах дилеммы заключенных, при этом демонстрируют порой озадачивающее, а порой более предсказуемое поведение. Эксперименты, проведенные с использованием компьютерного моделирования, дали аналогичные результаты. Примеры реальных дилемм заключенных приведены для того, чтобы вы получили представление о разнообразии ситуаций, в которых они возникают, и увидели, что по крайней мере в одном случае игроки могут отыскать собственное решение такой дилеммы.
1. Исходная игра (обзор)
Прежде чем приступить к анализу методов, позволяющих избежать неблагоприятного исхода в дилемме заключенных, ознакомимся с кратким описанием основ этой игры, вспомнив , которых подозревают в убийстве. Мужа и жену допрашивают отдельно, при этом каждый из них может либо признаться в совершении преступления, либо полностью отрицать свою причастность к нему. Таблица выигрышей, которые они при этом получат, представлена на и воспроизведена на рис. 10.1. Выигрыши исчисляются в годах тюремного заключения; следовательно, низкие значения более выгодны обоим игрокам.

Рис. 10.1. Таблица выигрышей в стандартной игре «дилемма заключенных»
В этой игре у обоих игроков есть доминирующая стратегия. Каждому из них выгоднее сознаться независимо от того, что сделает другой. В случае равновесного исхода оба игрока принимают решение признать свою вину и каждый получает 10 лет тюрьмы. Однако если бы оба решили все отрицать, это бы обеспечило им более благоприятный исход — всего по 3 года тюремного заключения.
В любой игре «дилемма заключенных» обязательно есть стратегия сотрудничества и стратегия обмана, или стратегия отказа от сотрудничества. На «отрицать вину» — это стратегия сотрудничества; ее использование обоими игроками обеспечивает им самый благоприятный исход. «Признать вину» — стратегия обмана, или отказа от сотрудничества; игроки обычно применяют ее в надежде на получение личной выгоды за счет соперника. Таким образом, участников игры «дилемма заключенных» можно обозначить в соответствии с их выбором стратегии либо как игроков, которые отказываются от сотрудничества, либо как игроков, которые идут на сотрудничество. Мы будем использовать эту классификацию при анализе возможных решений дилеммы заключенных.
Обратите внимание, что хотя мы говорим о стратегии сотрудничества, дилемма заключенных относится к числу некооперативных игр в том смысле, о котором шла речь в , а именно — игроки принимают решения и реализуют их отдельно друг от друга. Если бы два игрока могли обсуждать, выбирать и применять свои стратегии (например, если бы они находились в одном помещении и совместно решали, как им лучше поступить), у них не возникло бы проблем с получением исхода, предпочтительного для обоих. По сути, вопросы о том, когда и как может быть решена дилемма заключенных, сводятся к преодолению проблемы достижения кооперативного (предпочтительного для обоих игроков) исхода посредством некооперативных (индивидуальных) действий.
2. Категория решений I: повторение
Наиболее известный и естественный механизм, позволяющий поддерживать сотрудничество в дилемме заключенных, — это повторяющаяся игра. Повторяющееся или постоянное взаимодействие между игроками подразумевает наличие особых характеристик игр, которые они ведут друг с другом. В дилемме заключенных это проявляется в опасении каждого игрока по поводу того, что один случай отказа от сотрудничества приведет к его прекращению в будущем. Если ценность будущего сотрудничества достаточно велика и превышает выгоду, получаемую от отказа от него в краткосрочной перспективе, то долгосрочные личные интересы игроков могут автоматически удержать их от обмана без какой-либо необходимости в дополнительных мерах наказания или давления со стороны третьих лиц.
Проанализируем дилемму заключенных в контексте представленной в — Xavier’s Tapas и Yvonne’s Bistro. Для пущего эффекта мы решили ее упростить, оставив только два варианта цен: наилучшую цену (основанную на сговоре) для обоих ресторанов 26 долларов и цену 20 долларов в случае равновесия Нэша. Выигрыши (прибыль, выраженная в сотнях долларов в месяц; показаны на рис. 10.2) можно вычислить с помощью функций количества (спроса), приведенных в . Как и в любой дилемме заключенных, у каждого ресторана есть доминирующая стратегия — обмануть конкурента и назначить меньшую цену 20 долларов, хотя оба ресторана предпочли бы исход, предполагающий сотрудничество и более высокую цену в размере 26 долларов за блюдо.
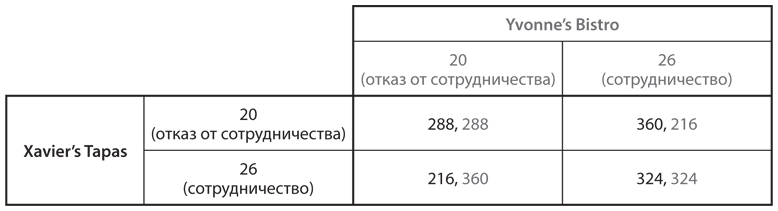
Рис. 10.2. Дилемма заключенных в контексте игры в ценообразование (в сотнях долларов в месяц)
Для начала предположим, что два ресторана сотрудничают друг с другом, установив более высокую цену 26 долларов. Если один из них (скажем, Xavier’s) отклонится от данной стратегии ценообразования, он увеличит месячную прибыль с 324 до 360 (с 32 400 до 36 000 долларов). Однако это означает обман, поэтому у ресторана Yvonne’s (конкурент Xavier’s) не будет причин для дальнейшего сотрудничества. Как только договоренности будут нарушены, прибыль Xavier’s составит 288 (28 800 долларов) в месяц, а не 324 (32 400 долларов), которые он мог бы иметь, если бы держал слово. Получив за один месяц на 36 (3600 долларов) больше благодаря обману, ресторан Xavier’s с этого момента начинает терять по 36 (3600 долларов) ежемесячно, разрушив сотрудничество с конкурентом. Даже если эти рестораны поддерживают отношения всего на протяжении трех месяцев, обман все равно не отвечает интересам Xavier’s. Аналогичные аргументы актуальны и для ресторана Yvonne’s. Таким образом, если бы они конкурировали друг с другом хотя бы три месяца, по всей вероятности, мы наблюдали бы их согласованные действия и высокие цены, а не обман и низкие цены, что прогнозирует теория в случае однократной игры.
А. Конечное повторение
На самом деле решение данной дилеммы не такое простое, как кажется. Что если взаимодействие между игроками длится ровно три месяца? Тогда стратегически мыслящие владельцы ресторанов захотят проанализировать полную трехмесячную игру и выбрать оптимальную стратегию ценообразования. С помощью анализа методом обратных рассуждений каждый из них определит, какую цену следует назначать в каждом месяце. Начав анализ с третьего месяца, они бы поняли, что на этом этапе нет будущего взаимодействия, требующего рассмотрения. И каждый ресторан пришел бы к выводу, что его доминирующая стратегия — «отказ от сотрудничества». Исходя из этого, в течение второго месяца фактически также отсутствует взаимодействие, требующее анализа, а значит, и здесь в качестве доминирующей выступает стратегия «отказ от сотрудничества». Та же аргументация применима и к первому месяцу. Поскольку оба ресторана выбирают стратегию «отказ от сотрудничества» во втором и третьем месяце, сотрудничество теряет для них ценность и в первый месяц. Иными словами, оба игрока изначально выбирают стратегию «отказ от сотрудничества», а это означает, что дилемма по-прежнему не решена.
Этот результат носит общий характер. Если отношения между участниками игры «дилемма заключенных» длятся фиксированный и известный промежуток времени, равновесие в доминирующих стратегиях «отказ от сотрудничества» должно преобладать на последнем этапе игры. Когда игроки приближаются к ее концу, взаимодействие теряет для них ценность, поэтому они и отказываются от него. Тогда анализ методом обратных рассуждений предсказывает такой отказ на протяжении всего пути игры, вплоть до ее начала. Тем не менее на практике участники конечно повторяющихся игр категории «дилемма заключенных» демонстрируют склонность к сотрудничеству, но мы поговорим об этом более подробно чуть позже.
Б. Бесконечное повторение
Анализ конечно повторяющейся дилеммы заключенных показывает, что даже повторение игры не может гарантировать игрокам решения их дилеммы. Но что произойдет, если взаимодействие между участниками игры не будет иметь заранее оговоренной продолжительности? Что если рестораны планируют конкурировать друг с другом в течение неопределенного времени? Тогда наш анализ должен учитывать этот новый аспект их взаимодействия и мы увидим, что стимулы игроков также изменятся.
В повторяющихся играх любого типа последовательный характер отношений между игроками означает, что они могут выбирать стратегии в зависимости от поведения в предыдущих раундах игры. Такие стратегии известны как условные стратегии, а ряд их конкретных примеров часто используется в теории повторяющихся игр. Большинство условных стратегий относятся к категории триггерных стратегий. Игрок, применяющий триггерную стратегию, поддерживает сотрудничество до тех пор, пока соперник (соперники) тоже это делает, но любой обман со стороны последнего «запускает» период наказания определенной продолжительности, на протяжении которого этот игрок отказывается от сотрудничества в ответ. Две наиболее известные триггерные стратегии — это стратегия бесповоротного наказания и стратегия равноценных ответных действий. Первая подразумевает взаимодействие с соперником вплоть до его отказа от него; как только соперник хотя бы раз выберет «отказ от сотрудничества», вы наказываете его, применяя стратегию «отказ от сотрудничества» в каждом очередном раунде игры до ее завершения. Вторая, или стратегия «око за око», — не столь безжалостна и известна (или печально известна) своей способностью решать дилемму заключенных без необходимости применения бессрочного наказания. Стратегия «око за око» сводится к следующему: игрок выбирает сотрудничество в первом раунде игры, а затем в каждом очередном раунде выбирает действия, выбранные соперником в предыдущем раунде. Таким образом, в случае применения стратегии равноценных ответных действий вы взаимодействуете с соперником, если он тоже выбрал сотрудничество в предыдущем раунде игры, и отказываетесь от него (в качестве наказания), если соперник отказался. Вы вернетесь к сотрудничеству после того, как ваш соперник выберет его в предыдущем раунде игры.
Давайте посмотрим, как бы протекала повторяющаяся игра в ценообразование в ресторанах, если бы один из игроков использовал условную стратегию равноценных ответных действий. Мы уже видели, что если ресторан Xavier’s Tapas откажется от сотрудничества на протяжении одного месяца, это может увеличить его прибыль на 36 (то есть он получит выигрыш 360 вместо 324). Но если конкурент выберет стратегию «око за око», такой отказ приведет к тому, что в следующем месяце ресторан Yvonne’s Bistro накажет Xavier’s Tapas в качестве ответной меры. При этом у Xavier’s есть два варианта выбора. Первый — отказаться от сотрудничества, назначив цену 20 долларов, и подвергнуться наказанию со стороны ресторана Yvonne’s согласно стратегии «око за око»; в этом случае ресторан Xavier’s будет терять 36 (то есть его выигрыш составит 288 вместо 324) ежемесячно в обозримом будущем. Такой сценарий развития событий кажется весьма затратным. Но Xavier’s Tapas мог бы при желании восстановить сотрудничество. Вернувшись к кооперативной цене 26 долларов через месяц, ресторан Xavier’s подвергся бы наказанию со стороны ресторана Yvonne’s всего в течение одного месяца и понес бы за это время убытки в размере 108 (выигрыш 216 вместо 324, если бы не отказывался от сотрудничества). А на следующий месяц оба ресторана вернулись бы к кооперативной цене, которая приносила бы им ежемесячную прибыль 324. Такой одноразовый отказ от сотрудничества обеспечивает дополнительную прибыль в размере 36, но влечет за собой дополнительный убыток 108 на протяжении периода наказания. Очевидно, что это также весьма затратный вариант для ресторана Xavier’s Tapas.
Однако здесь важно понимать, что вследствие отказа от сотрудничества ресторан Xavier’s получает дополнительных 36 долларов на протяжении первого месяца, тогда как его убытки переносятся на будущее. Следовательно, относительная важность прибыли и убытков зависит от относительной важности настоящего по отношению к будущему. Поскольку в данном примере выигрыши исчисляются в долларах, можно выполнить объективное сравнение. Как правило, деньги (или прибыль), заработанные сегодня, лучше денег, заработанных завтра, потому что, если они вам какое-то время не понадобятся или у вас не будет желания их тратить, вы можете инвестировать их сейчас и получать на них доход до тех пор, пока они вам не понадобятся. В связи с этим Xavier’s Tapas должен определить, стоит ли отказываться от сотрудничества с конкурентом, воспользовавшись общей рентабельностью этой инвестиции (рассчитанной с учетом дохода от прироста капитала и (или) дивидендов и (или) процентов, в зависимости от типа инвестирования). Обозначим данный показатель доходности инвестиций символом r. Таким образом, один инвестированный доллар приносит r долларов в виде процентов и (или) дивидендов и (или) дохода от прироста капитала, или 100 долларов приносят 100r; поэтому иногда говорят, что норма прибыли составляет 100r процентов.
Обратите внимание, что мы можем определить, заинтересован ли ресторан Xavier’s в отказе от сотрудничества, благодаря тому, что его выигрыши выражены в денежных единицах, а не в обычных показателях степени важности исходов, как в некоторых играх, представленных в предыдущих главах книги (например, в главах 3–6). Это означает, что значения выигрышей в разных ячейках непосредственно сопоставимы: в данном примере выигрыш 4 (доллара) в два раза лучше выигрыша 2 (доллара), тогда как выигрыш 4 не всегда ровно в два раза лучше выигрыша 2 в любой игре два на два, в которой четыре возможных исхода имеют рейтинг от 1 (самый плохой исход) до 4 (самый лучший исход). Выигрыши участников игры, исчисляемые в единицах, поддающихся количественной оценке, позволяют определить, выбирать ли стратегию отказа от сотрудничества в дилемме заключенных.
I.-Стоит ли один раз отказываться от сотрудничества в игре против соперника, выбирающего стратегию равноценных ответных действий? Один из вариантов выбора, имеющихся в распоряжении ресторана Xavier’s в повторяющейся игре против конкурента, использующего стратегию «око за око», — всего раз отказаться от кооперативного исхода, а затем вернуться к сотрудничеству. Это принесет ресторану прибыль 36 в первый месяц (при отказе от сотрудничества), но приведет к убыткам 108 во втором. На третий месяц сотрудничество возобновляется. Стоит ли отказываться от него всего на один месяц?
Мы не можем непосредственно сравнить прибыль 36 за первый месяц с убытком 108 за второй, поскольку в расчет необходимо включить дополнительную денежную стоимость времени. Иными словами, нам нужен способ, позволяющий определить, какую стоимость на протяжении первого месяца имеют 108 долларов убытка за второй месяц. Тогда мы сможем сопоставить полученное число с прибылью 36, чтобы решить, стоит ли отказываться от сотрудничества на один месяц. Величина, которую мы ищем, — это приведенная стоимость 108, или сумма прибыли, заработанной в текущем месяце (в настоящем), эквивалентная (имеющая такую же стоимость) 108, заработанным в следующем месяце. То есть нам необходимо вычислить, какая сумма, заработанная в текущем месяце, вместе с процентами составила бы 108 в следующем месяце. Мы называем это число приведенной стоимостью 108 (present value, PV).
Учитывая, что общая норма прибыли (за месяц) равна r, получение PV в этом месяце и инвестирование этой суммы до следующего месяца дает PV + rPV, где первый член — это основная сумма, возвращаемая инвестору, а второй — доход (в виде процентов, дивидендов или прироста капитала). Если общая сумма 108, тогда значение PV равно текущей стоимости 108. Равенство PV + rPV = 108 позволяет вычислить значение PV
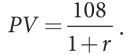
Теперь при любом значении r мы можем определить точную сумму в долларах, которая, будучи заработанной в текущем месяце, будет иметь стоимость 108 в следующем месяце.
С точки зрения Xavier’s Tapas, вопрос о том, компенсирует ли прибыль 36 за текущий месяц убыток 108 в следующем месяце, остается открытым. Ответ зависит от значения PV. Ресторан Xavier’s должен сравнить прибыль 36 с приведенной стоимостью убытка 108. Отказаться от сотрудничества с конкурентом один раз (а затем возобновить его) целесообразно только если 36 > 108/(1 + r). Это равносильно утверждению о том, что однократный отказ от сотрудничества приносит пользу лишь в случае, если 36(1 + r) > 108, что позволяет сократить это выражение до r > 2. Стало быть, ресторан Xavier’s должен выбирать стратегию однократного отказа от сотрудничества в игре против конкурента, применяющего стратегию «око за око», только если общая норма прибыли за месяц больше 200%. Такой исход весьма маловероятен; например, учетная ставка редко превышает 12%. Это означает, что месячная процентная ставка составляет менее 1% (и капитализируется один раз в год, а не ежемесячно), а это существенно меньше вычисленных нами 200%. Таким образом, ресторану Xavier’s лучше продолжать сотрудничество с конкурентом, чем пытаться один раз отказаться от него из-за выбора рестораном Yvonne’s стратегии «око за око».
II.-Стоит ли полностью отказываться от сотрудничества в игре против соперника, выбирающего стратегию равноценных ответных действий? А как насчет того, чтобы отказаться от сотрудничества раз и в дальнейшем продолжать делать это всегда? Этот вариант выбора сперва обеспечит ресторану Xavier’s прибыль 36, а затем ежемесячно начнет приносить убыток 36, если конкурент применит стратегию «око за око». Для того чтобы определить, отвечает ли такая стратегия интересам ресторана Xavier’s, снова необходимо вычислить приведенную стоимость понесенных убытков. Однако на этот раз они будут понесены за бесконечный интервал предстоящих месяцев конкуренции.
Бессрочный отказ ресторана Xavier’s от сотрудничества в игре с конкурентом, использующим стратегию «око за око», обеспечивает последовательность выигрышей (прибыли), эквивалентную тому, что получил бы этот ресторан при отказе сотрудничать в игре против конкурента, применившего триггерную стратегию бесповоротного наказания. А она требует, чтобы игроки наказывали любой отказ от сотрудничества ответным отказом на протяжении всех будущих периодов. В таком случае ресторану Xavier’s не стоит даже пытаться возобновлять взаимодействие после первого отказа, поскольку с этого момента конкурент неизменно будет выбирать отказ от сотрудничества в качестве наказания. Любой отказ от сотрудничества со стороны ресторана Xavier’s в этом случае приведет к получению им прибыли 36 за первый месяц и последующей ежемесячной потере 36 — точно такой же исход, как и при бессрочном отказе от сотрудничества в игре против конкурента, использующего стратегию равноценных ответных действий. Следовательно, представленный ниже анализ также позволяет выяснить, целесообразно ли вообще применять стратегию отказа от сотрудничества в игре против соперника, использующего стратегию строгого наказания.
Для того чтобы это определить, необходимо вычислить приведенную стоимость всех убытков 36, понесенных в предстоящие месяцы, суммировать эти значения и сопоставить полученную сумму с прибылью 36 за первый месяц отказа от сотрудничества. Приведенная стоимость убытка 36, понесенного за первый месяц наказания и продолжающегося отказа ресторана Xavier’s сотрудничать, равна 36 / (1 + r); расчеты идентичны используемым в для вычисления того, что приведенная стоимость 108 равна 108/(1 + r). В следующем месяце значение PV должно представлять собой такую сумму в долларах за текущий месяц, которая вместе со сложными процентами за два месяца составила бы 36 через два месяца. Если PV инвестировать сейчас, то через месяц инвестор получит эту основную сумму плюс прибыль rPV, то есть в сумме PV + rPV, как и ранее. Если оставить эту общую сумму инвестированной на второй месяц, к концу двух месяцев инвестор получит инвестированную сумму в начале второго месяца (PV + rPV) плюс прибыль на эту сумму в размере r(PV + rPV). Значение PV убытка 36, понесенного через два месяца начиная с текущего момента, должно удовлетворять уравнению PV + rPV + r(PV + rPV) = 36. Из этой формулы мы можем вывести значение PV: PV(1 + r)2 = 36, или PV = 36/(1 + r)2. По всей вероятности, вы уже увидели закономерность. Значение PV убытка 36, понесенного за третий месяц бессрочного отказа от сотрудничества, составляет 36/(1 + r)3, а за четвертый — 36/(1 + r)4. В действительности значение PV убытка 36, понесенного за энный месяц бессрочного отказа от сотрудничества, составляет 36/(1 + r)n. Ресторан Xavier’s несет бесконечную сумму убытков 36, причем приведенная стоимость каждого такого убытка с каждым месяцем уменьшается.
Точнее говоря, при значениях n от n = 1 до n = ∞ (где n — месяцы бессрочного отказа от сотрудничества начиная с первого месяца, то есть месяца с номером 0) ресторан Xavier’s терпит убытки 36/(1 + r)n. В математическом виде это можно записать как сумму бесконечного количества членов
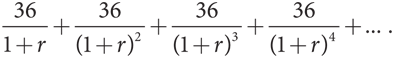
Поскольку r — это норма прибыли, которая должна быть положительным числом, множитель 1/(1 + r) будет меньше 1. Как правило, его называют коэффициентом дисконтирования и обозначают греческой буквой δ. Математическое правило вычисления бесконечных сумм при δ = 1/(1+r)<1 гласит, что эта сумма сводится к конкретному значению, в данном случае к 36/r.
Теперь мы можем определить, решит ли Xavier’s Tapas навсегда отказаться от сотрудничества с конкурентом. Ресторан сравнит прибыль 36 с приведенной стоимостью всех убытков 36, то есть 36/r, и в итоге навсегда откажется от сотрудничества, только если 36 > 36/r, или r > 1. Иными словами, в данной игре отказ от сотрудничества принесет выгоду тогда, когда месячная норма прибыли превысит 100%, что маловероятно. Следовательно, не стоит ожидать от ресторана Xavier’s отказа от взаимодействия в игре с сотрудничающим конкурентом, если оба используют стратегию «око за око». (То же самое касается ситуации, в которой оба разыгрывают стратегию бесповоротного наказания.) Когда оба ресторана применяют стратегию «око за око», кооперативный исход, при котором они устанавливают высокую цену, — и есть равновесие Нэша в этой игре. Выбор обоими игроками стратегии равноценных ответных действий создает равновесие Нэша, а значит, использование этой условной стратегии решает дилемму заключенных в игре между ресторанами.
Не забывайте о том, что стратегия равноценных ответных действий — лишь одна из многочисленных триггерных стратегий, применяемых игроками в повторяющихся дилеммах заключенных. И она одна из самых «мягких». Таким образом, если стратегия «око за око» подходит для решения дилеммы заключенных в игре между двумя ресторанами, значит, и другие, более жесткие стратегии, могут выполнить эту задачу. Как уже говорилось, стратегию бесповоротного наказания также можно использовать для поддержания сотрудничества как в этой бесконечно повторяющейся игре, так и в других играх.
В. Игры с неизвестной продолжительностью
В дополнение к анализу игр с конечной и бесконечной продолжительностью хотим предложить более сложный инструмент для решения игр с неизвестной продолжительностью. В некоторых повторяющихся играх участники могут не знать наверняка, сколько именно между ними будет длиться взаимодействие, но иметь определенное представление о вероятности того, что игра продлится еще один период. Например, наши рестораны могут считать, что их повторяющееся сотрудничество будет продолжаться только до тех пор, пока клиенты будут отдавать предпочтение комплексным обедам, но если в течение каждого месяца появляется вероятность того, что клиенты начнут выбирать блюда по меню, характер игры изменится.
Напоминаем, что приведенная стоимость убытка за следующий месяц уже равна произведению δ = 1/(1 + r) на заработанную сумму. Если в дополнение к этому существует только вероятность p (меньше 1) того, что игроки будут сотрудничать и в следующем месяце, то убыток за следующий месяц составит всего лишь произведение p на δ Для ресторана Xavier’s Tapas это означает, что PV убытка 36, понесенного при условии бессрочного отказа от сотрудничества, равно 36 × δ [то же, что и 36 / (1 + r)], когда предполагается, что игра точно продолжится, и всего 36 × p × δ, когда игра продолжится с вероятностью p. Включение в расчеты вероятности того, что игра может закончиться в следующем периоде, означает, что приведенная стоимость убытка 36 меньше (поскольку p < 1), чем в случае, когда игра точно будет продолжаться (то есть когда p предположительно равно 1).
Благодаря включению в расчеты вероятности p мы теперь дисконтируем будущие выигрыши на коэффициент p × δ, а не δ. Мы называем эту величину фактическим коэффициентом дисконтирования R, где 1/(1 + R) = p × δ; при этом между R и p и δ существует следующая зависимость:
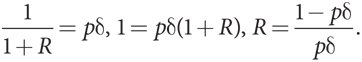
Если фактическая норма прибыли на инвестиции составляет 5% (r = 0,05, а значит, δ = 1/1,05 = 0,95), а вероятность того, что игра продолжится в следующем месяце, равна 50% (p = 0,5), тогда R = [1 – (0,5)(0,95)] / [(0,5)(0,95)] = 1,1, или 110%.
В этих примерах высокая норма прибыли, необходимая для расторжения сотрудничества, покажется более реалистичной, если назвать ее эффективной, а не фактической нормой прибыли. Теперь становится понятно, что бессрочный или даже однократный отказ от сотрудничества действительно может принести игроку выгоду при наличии достаточно большой вероятности того, что игра закончится в ближайшем будущем. Рассмотрим в качестве примера решение ресторана Xavier’s по поводу того, стоит ли навсегда отказываться от сотрудничества с конкурентом, использующим стратегию «око за око». Предыдущие расчеты показали, что бессрочный отказ от сотрудничества выгоден только тогда, когда r больше 1, или 100%. Если фактическая норма прибыли ресторана Xavier’s составит 5%, а вероятность того, что игра продолжится в следующем месяце, равна 50%, как мы предположили выше, то норма прибыли в размере 110% превышает критическое значение, необходимое для продолжения отказа от сотрудничества. Таким образом, кооперативное поведение, поддерживаемое стратегией «око за око», может оказаться под вопросом, если имеется довольно большая вероятность того, что повторяющаяся игра может закончиться к концу следующего раунда, а именно к моменту получения достаточно малого значения p.
Г. Общая теория
Мы можем без труда обобщить идеи в отношении целесообразности отказа от сотрудничества с соперниками, использующими стратегию «око за око», с тем чтобы вы могли применять их в любой дилемме заключенных. Для этого мы используем таблицу (рис. 10.3) с общими выигрышами (выраженными в надлежащих единицах), которые соответствуют стандартной структуре выигрышей в дилемме заключенных. Эти выигрыши должны удовлетворять условию B > K > О > H, где К — кооперативный исход; О — отказ обоих игроков от сотрудничества; В — высокий выигрыш, получаемый игроком, отказавшимся от сотрудничества, в случае если другой игрок продолжает сотрудничать; и Н — низкий выигрыш, получаемый проигравшим (игрок, продолжающий сотрудничать) в той же ситуации.
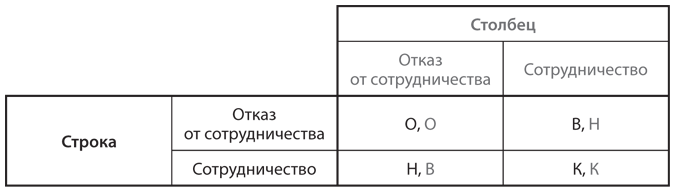
Рис. 10.3. Общая версия дилеммы заключенных
В этой общей версии дилеммы заключенных разовая прибыль игрока, полученная за счет отказа от сотрудничества, составляет (B – K). Убыток за один период, понесенный в связи с наказанием, когда вы возобновляете сотрудничество, равен (K – H), а убыток за каждый очередной период в случае бессрочного отказа от сотрудничества составляет (K – О). Для того чтобы максимально обобщить расчеты, примем во внимание ситуации, в которых существует вероятность p < 1 того, что игра продолжится и после окончания следующего периода; таким образом мы дисконтируем выигрыши с помощью фактической нормы прибыли R за каждый период. Если p = 1 (как в случае гарантированного продолжения игры), то R = r, простая процентная ставка, используемая нами в предыдущих вычислениях. Заменив r на R, мы увидим, что полученные ранее результаты обобщаются буквально сразу же.
Мы уже пришли к выводу, что игрок отказывается от сотрудничества ровно один раз в игре против соперника, использующего стратегию равноценных ответных действий, если разовая прибыль (B – K), полученная в результате, превышает приведенную стоимость убытка за один период, понесенного в связи с наказанием (приведенная стоимость K – H). В общей игре это означает, что игрок один раз отказывается от сотрудничества с соперником, применяющим стратегию равноценных ответных действий, только когда (B – K) > (K – H) / (1 + R), или (1 + R)(B – K) > K – H, или
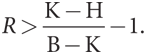
Аналогичным образом мы выявили, что игрок навсегда отказывается от сотрудничества с соперником, использующим стратегию «око за око», только если полученная в результате разовая прибыль превышает приведенную стоимость бесконечной суммы убытков за отдельные периоды, понесенных в связи с бессрочным отказом от сотрудничества (где убыток за период составляет K – О). В общей версии игры игрок навсегда отказывается от сотрудничества с соперником, использующим стратегию «око за око» или стратегию бесповоротного наказания, только если (B – K) > (K – О) / R или
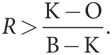
Как следует из этих двух формул, существует три важных аспекта принятия игроком решения об отказе от сотрудничества: непосредственная прибыль от такого отказа (B – K); будущие убытки, понесенные в связи с наказанием (K – H или K – О за период наказания), и значение фактической нормы прибыли (R, которая отражает важность настоящего по сравнению с будущим). При каких условиях по этим трем значениям игроки заинтересованы в отказе от сотрудничества?
Во-первых, предположим, что значения прибыли и убытков, связанных с отказом от сотрудничества, фиксированы. От изменения значения R зависит, откажется ли игрок от сотрудничества, причем чем больше значение R, тем выше вероятность отказа. Большие значения R связаны с малыми значениями p и δ (а также более высокими значениями r), поэтому вероятность отказа сотрудничать повышается при наличии незначительной перспективы продолжения или низкого коэффициента дисконтирования (или высокой процентной ставки). Об этом можно еще сказать так: отказ от сотрудничества более вероятен, когда настоящее важнее будущего или когда будущего не так много, чтобы его можно было принимать в расчет. Иными словами, отказ от сотрудничества более вероятен, если игроки нетерпеливы или считают, что игра быстро закончится.
Во-вторых, проанализируем ситуацию, когда фактическая норма прибыли будет фиксированной, как в случае прибыли за один период, полученной за счет отказа от сотрудничества. В такой ситуации целесообразность отказа от сотрудничества зависит от изменения величины убытков за каждый период, понесенных в связи с наказанием. Здесь именно меньшие значения К–Н или К–Н стимулируют отказ от сотрудничества, то есть он более вероятен, когда наказание не слишком суровое.
И наконец, допустим, что фактическая норма прибыли и убытки за каждый период, понесенные в связи с наказанием, — постоянные величины. Теперь игроки, скорее всего, откажутся от сотрудничества при высоком значении прибыли B – K. Эта ситуация более вероятна, когда отказ от сотрудничества обеспечивает игроку явные преимущества в ближайшем будущем.
Данный анализ также подчеркивает важность обнаружения случаев прекращения взаимодействия. Принятие решений о его продолжении зависит от того, как долго такой отказ не будет обнаружен, насколько точно он будет выявлен и сколько может длиться наказание, прежде чем будет предпринята попытка возобновить сотрудничество. Наша модель не учитывает всех этих факторов в явной форме, но позволяет сделать следующий вывод: если отказ от сотрудничества поддается быстрому и точному обнаружению, его преимущества не будут иметь долгосрочного эффекта, но впоследствии придется понести определенные издержки. Таким образом, эффективность любой триггерной стратегии в решении повторяющейся дилеммы заключенных зависит от того, насколько филигранно (как в плане оперативности, так и точности) игроки смогут обнаружить отказ от сотрудничества. Это одна из причин, почему стратегию равноценных ответных действий часто считают опасной: малейшая ошибка в выполнении действий или в их восприятии способна повлечь за собой бесконечный цикл наказания, вырваться из которого не удастся до тех пор, пока не будет совершена хотя бы малейшая ошибка противоположного типа.
Вы можете использовать все эти идеи для того, чтобы определить, когда ожидать более тесного сотрудничества между соперниками, а когда отказа от него, а то и более жестких действий. Например, в плохие времена, когда целая отрасль оказывается на грани краха и компании чувствуют, что у них нет будущего, конкурентная борьба может существенно ожесточиться (реже может наблюдаться кооперативное поведение). Даже когда временно наступает хороший период, но никто не рассчитывает на его длительность, компании могут воспользоваться этим, чтобы заработать быструю прибыль, поэтому кооперативное поведение может снова игнорироваться. Точно так же в отрасли, сформировавшейся под влиянием моды, крах которой неминуем, когда мода изменится, проявляется меньше склонности к сотрудничеству. Так, конкретный морской курорт может стать любимым местом отдыха туристов, но все местные отели должны знать, что такая ситуация вряд ли продлится вечно, поэтому они не могут себе позволить сговор по поводу ценообразования. С другой стороны, когда меняется мода на продукты, выпускаемые неизменной группой компаний, поддерживающих долгосрочные отношения, партнерство сохраняется. Например, даже если всех детей будут интересовать плюшевые мишки в течение одного года и боты-спасатели из «Трансформеров» в течение следующего года, сговор относительно ценообразования может иметь место только в случае, если одна и та же небольшая группа производителей выпускает оба продукта.
В мы более подробно проанализируем дилемму заключенных, возникающую в играх со многими участниками, и исследуем, когда и как игроки могут преодолеть эту дилемму и обеспечить более благоприятный для всех игроков исход.
3. Категория решений II: взыскание и вознаграждение
Хотя повторение — основной инструмент решения дилеммы заключенных, существует еще ряд инструментов, которые можно использовать для достижения этой цели. Один из самых простых способов предотвратить дилемму заключенных в однократной версии игры — наложить на игроков прямое взыскание в случае отказа от сотрудничества. Когда в выигрыши вносятся изменения с учетом издержек, понесенных в связи с наложением взыскания, игроки могут обнаружить, что дилемма уже решена.
Рассмотрим дилемму заключенных в игре с участием мужа и жены, о которой шла речь в . Если один игрок применит стратегию «отказ от сотрудничества», исход игры будет таким: 1 год тюрьмы для этого игрока и 25 лет тюрьмы для игрока, выбравшего стратегию «сотрудничество». Однако после окончания столь малого срока заключения игрока, который отказался от сотрудничества, у ворот тюрьмы могут ждать друзья другого игрока. Физический вред, причиненный ему этими друзьями, может быть эквивалентен дополнительным 20 годам лишения свободы. Если это действительно так и игроки учитывают вероятность подобного сценария, то структура выигрышей в исходной игре изменится.
Новая игра, в которой выигрыши рассчитаны с учетом физической расправы, представлена на рис. 10.4. Когда к приговору каждого игрока прибавляются еще 20 лет тюремного заключения, если один игрок сознаётся, а другой все отрицает, игра выглядит совсем по-другому.

Рис. 10.4. Дилемма заключенных с наложением взыскания в случае, если один игрок выберет стратегию «отказ от сотрудничества»
Поиск доминирующих стратегий на рисунке показывает, что их нет. Дальнейшее сравнение ячеек позволяет определить, что в игре появились два равновесия Нэша в чистых стратегиях. Одно — исход «признать вину» / «признать вину», другое — исход «отрицать вину» / «отрицать вину». Теперь каждый игрок понимает, что он заинтересован в сотрудничестве, если другой игрок тоже будет это делать. Игра изменилась: она перестала быть дилеммой заключенных и превратилась в игру в доверие, рассмотренную в . Решение новой игры требует выбора одного из двух существующих равновесий. Очевидно, что одно из них (кооперативный исход) лучше другого с точки зрения обоих игроков. Следовательно, если в игре достижима определенная сходимость ожиданий, это равновесие можно использовать в качестве фокальной точки.
Обратите внимание, что в этом сценарии взыскание налагается на игрока, отказавшегося сотрудничать, только тогда, когда его соперник не отказывается это делать. Однако в дилемме заключенных можно использовать более строгое взыскание, например взыскание за любое признание. Как правило, такие дисциплинарные меры должна принимать третья сторона, имеющая определенную власть над двумя игроками, а не друзья другого игрока, поскольку у них не будет полномочий наказывать первого игрока, если второй также откажется сотрудничать. Если оба заключенных — члены той или иной организации (например, банды или мафиозной группировки) и в ней действует правило, согласно которому ее члены ни при каких обстоятельствах не должны ни в чем сознаваться полиции, иначе их ждет жестокая физическая расправа, то игра снова меняется и превращается в игру, представленную на рис. 10.5.

Рис. 10.5. Дилемма заключенных с наложением взыскания в случае любого отказа от сотрудничества
Теперь выигрыш, эквивалентный дополнительным 20 годам тюремного заключения, прибавляется ко всем выигрышам, связанным со стратегией «признать вину» (сравните рис. 10.5 и ). В новой игре, как и в исходной, у каждого игрока есть доминирующая стратегия. Но разница в том, что изменение выигрышей делает стратегию «отрицать вину» доминирующей для каждого игрока. А исход «отрицать вину» / «отрицать вину» становится единственным равновесием Нэша в чистых стратегиях. Более строгая схема наложения взыскания, выполнение которой обеспечивает третья сторона, делает отказ от сотрудничества настолько невыгодным для игроков, что кооперативный исход становится в этой игре новым равновесием.
В более крупных играх категории «дилемма заключенных» возникают трудности с применением взысканий. В частности, схемы их наложения сложнее поддерживать, если в игре участвует много игроков и присутствует некоторая неопределенность. В таких играх труднее установить, действительно ли мы имеем дело с отказом от сотрудничества или это просто невезение или ошибочный ход. Кроме того, если кто-то из игроков на самом деле отказался сотрудничать, зачастую его бывает трудно вычислить среди других игроков. А в однократной игре отсутствует возможность в будущем скорректировать взыскание, если оно оказалось слишком строгим, или наложить взыскание, когда игрок, отказавшийся сотрудничать, все же был выявлен. Таким образом, в крупных однократных играх взыскание может быть менее эффективным, чем в игре с двум участниками, которую мы здесь анализируем. В мы более подробно рассмотрим различные примеры дилеммы заключенных с большим количеством игроков.
Еще одна интересная возможность возникает в случае, когда решенная с помощью схемы наложения взыскания дилемма заключенных рассматривается в контексте более крупного сообщества, в котором проходит эта игра. Может сложиться ситуация, когда равновесный исход дилеммы заключенных неблагоприятен для ее участников, но приносит пользу обществу в целом или его определенной группе. Поэтому не исключено социальное или политическое давление, направленное на минимизацию шансов игроков преодолеть дилемму. Если в качестве решения дилеммы заключенных выступает взыскание, налагаемое третьей стороной (как в случае мафии, требующей молчать при любых обстоятельствах), общество может разработать свою стратегию снижения его эффективности. Федеральная программа защиты свидетелей — один из примеров системы, созданной именно с этой целью. Правительство США устраняет угрозу расправы в обмен на признания и свидетельские показания в суде.
Аналогичные ситуации встречаются и в других примерах дилеммы заключенных, как, скажем, в игре в ценообразование между двумя ресторанами. Равновесие в ней подразумевало, что оба ресторана назначат низкую цену 20 долларов, хотя они получили бы более высокую прибыль, установив высокую цену 26 долларов. Хотя рестораны хотели бы предотвратить этот «неблагоприятный» исход (а мы уже видели, что использование триггерных стратегий позволяет им это сделать), низкие цены, которые обеспечивает равновесие Нэша в однократной игре, больше радуют их клиентов. Более того, клиенты заинтересованы снизить действенность любого механизма принуждения или процесса решения дилеммы, который могут использовать рестораны. Например, поскольку иногда компании, столкнувшиеся с дилеммой заключенных в контексте игры в ценообразование, пытаются решить ее посредством кампаний «не ищите дешевле» или «гарантия лучшей цены», клиенты могут потребовать принять законы, запрещающие применение подобных методов. Мы проанализируем последствия таких стратегий компенсации разницы в цене в .
Дилемму заключенных можно решить не только путем наказания игроков, отказавшихся от сотрудничества, но и посредством вознаграждения игроков, которые его предпочли. Поскольку такое решение трудно реализуемо на практике, мы лишь кратко остановится на нем.
Самый важный вопрос — кто должен выплачивать вознаграждение. Если третья сторона (один человек или группа), то ее заинтересованность в сотрудничестве между игроками должна быть достаточной, чтобы оправдать целесообразность такой выплаты. Один из редких примеров подобной ситуации — посредничество США при заключении Кэмп-Дэвидских соглашений между Израилем и Египтом, когда Штаты пообещали обеим странам солидную помощь.
Если выплачивать друг другу вознаграждение должны сами игроки, то его необходимо сделать условным (выплачивается только в случае сотрудничества другого игрока) и достоверным (гарантированно выплачивается в случае сотрудничества другого игрока). Для удовлетворения этим критериям следует заключить особое соглашение. Например, игрок, дающий обещание, должен заранее внести определенную сумму на счет условного депонирования, принадлежащий порядочному и нейтральному третьему лицу, которое передаст ее другому игроку, если тот выберет сотрудничество, или вернет первому игроку, если второй откажется взаимодействовать. В показано, как действуют такие договоренности.
4. Категория решений III: лидерство
Третий метод решения дилеммы заключенных относится к ситуациям, в которых один игрок берет на себя роль лидера во взаимодействии. В большинстве примеров дилеммы заключенных эта игра считается симметричной. Иными словами, все игроки теряют или получают одну и ту же сумму при отказе от сотрудничества и при согласии сотрудничать. Однако в реальных стратегических ситуациях один игрок может быть относительно «крупным» (лидером), а другой — «мелким». Если размер выигрышей неравноценен, отказ от сотрудничества способен нанести более крупному игроку такой вред, что он может пойти на сотрудничество, даже зная, что другой игрок может отказаться от него. Например, Саудовская Аравия много лет играла в ОПЕК (Организации стран — экспортеров нефти) роль «стабилизирующего производителя»: для поддержания высокой цены на нефть она сокращала ее добычу, в то время как один из более мелких производителей (таких как Ливия) увеличивал.
Как в примере с ОПЕК, лидерство чаще наблюдается в играх между странами, чем между компаниями или отдельными людьми. Именно поэтому в качестве примера игры, в которой лидерство можно использовать для решения дилеммы заключенных, мы выбрали игру между странами. Представьте, что населению двух стран, Дорминики и Софории, угрожает болезнь под названием SANE (Sudden Acute Narcoleptic Episodes — «внезапные резкие приступы нарколепсии»). Заболевание поражает одного человека из 2000, или 0,05% от общей численности населения, и приводит к тому, что жертва впадает в состояние глубокого сна на целый год. У болезни нет осложнений, но издержки, связанные с выпадением работника из экономической жизни страны на год, составляют 32 000 долларов. В каждой стране по 100 миллионов трудоспособного населения, поэтому ожидаемое количество случаев заболевания в каждой составляет 50 000 (0,0005 × 100 000 000), а ожидаемые издержки в связи с распространением болезни равны 1,6 миллиарда долларов (50 000 × 32 000). Общий ожидаемый уровень издержек в связи с болезнью во всем мире (то есть в Дорминике и Софории) составляет при этом 3,2 миллиарда долларов.
Ученые убеждены, что интенсивная программа исследований стоимостью 2 миллиарда долларов позволит найти стопроцентно эффективную вакцину. Сравнение стоимости этой исследовательской программы с уровнем издержек в связи с распространением болезни во всем мире показывает, что, с точки зрения населения в целом, программу следует реализовать. Однако правительство каждой страны должно рассмотреть вопрос о том, стоит ли ему в одиночку финансировать всю исследовательскую программу. Правительства двух стран принимают решения независимо друг от друга, но от этих решений зависит исход игры для обеих стран. В частности, если правительство одной страны берется финансировать весь проект, население другой страны сможет получить доступ к информации и найдет вакцину без всяких затрат. Тем не менее выигрыш каждого правительства зависит только от издержек, понесенных населением его страны.
Матрица этой некооперативной игры представлена на рис. 10.6. Каждая страна выбирает из двух стратегий: «провести исследования» и «не проводить исследований»; выигрыши отображают выраженные в миллиардах долларов издержки двух стран в случае различных комбинаций стратегий. Несложно определить, что эта игра представляет собой дилемму заключенных и что «не проводить исследования» — доминирующая стратегия каждой страны.

Рис. 10.6. Выигрыши в игре «исследования по преодолению болезни SANE» между двумя странами с одинаковой численностью трудоспособного населения (выигрыши выражены в миллиардах долларов)
А теперь предположим, что в этих странах неодинаковая численность трудоспособного населения — 150 миллионов в Дорминике и 50 миллионов в Софории. В таком случае, если ни одно правительство не станет финансировать исследования, издержки Дорминики в связи с распространением SANE составят 2,4 миллиарда долларов (0,0005 × 150 000 000 × 32 000), а Софории — 0,8 миллиарда долларов (0,0005 × 50 000 000 × 32 000). Измененная матрица игры представлена на рис. 10.7.

Рис. 10.7. Выигрыши в игре «исследования по преодолению болезни SANE» между двумя странами с неодинаковой численностью трудоспособного населения (выигрыши выражены в миллиардах долларов)
В этой версии игры «не проводить исследований» по-прежнему доминирующая стратегия Софории. Однако теперь наилучший ответ Дорминики — «провести исследования». Что привело ее к изменению выбора стратегии? Очевидно, что ответ кроется в неравномерном распределении населения в измененной версии игры. Теперь на долю Дорминики может выпасть настолько большая часть общих издержек в связи с распространением болезни, что страна посчитает целесообразным самостоятельно провести необходимые исследования, причем даже в случае, если ей известно, что Софория намерена сыграть роль «безбилетника» и воспользоваться их результатами.
Игра в исследования, представленная на , — уже не дилемма заключенных. Здесь мы видим, что дилемма в каком-то смысле уже «решена» асимметричностью масштаба игроков. Более крупная страна предпочитает взять на себя роль лидера и принести пользу всему миру.
Ситуации с лидерством, в которых при иных обстоятельствах могла бы присутствовать дилемма заключенных, часто встречаются в международной дипломатии. Зачастую роль лидера естественным образом достается самым крупным или самым авторитетным игрокам (этот феномен известен как «эксплуатация сильных слабыми»). Например, долгие годы после Второй мировой войны Соединенные Штаты Америки несли на себе непропорционально большую долю расходов в оборонительных союзах, таких как НАТО, а также продвигали идею свободной международной торговли, тогда как партнеры, в частности Япония и Европа, склонялись к более протекционистской политике. Возможно, в подобных ситуациях было бы разумно предположить, что более крупный или авторитетный игрок может взять на себя роль лидера, поскольку его интересы тесно связаны с интересами всей совокупности игроков; если на крупного игрока приходится значительная часть группы, такое переплетение интересов кажется очевидным и от крупного игрока ожидают более кооперативных действий, чем при других обстоятельствах.
5. Экспериментальные данные
Многие исследователи проводили эксперименты, участники которых соперничали друг с другом в различных вариантах дилеммы заключенных. Как показывают результаты этих экспериментов, сотрудничество в таких играх возможно и действительно наблюдается, причем даже в повторяющихся играх с известной или конечной продолжительностью. Многие игроки начинают игру с сотрудничества и поддерживают его достаточно долго при условии, что соперник отвечает тем же. Отказ от сотрудничества появляется только в нескольких последних раундах игры. Хотя подобное поведение противоречит логике обратных рассуждений, оно может оказаться выигрышным, если придерживаться его в течение приемлемого срока. Пары участников таких игр получают более высокий выигрыш, чем получили бы рационально мыслящие, расчетливые стратеги посредством отказа от сотрудничества с самого начала игры.
Идея о том, что определенный уровень сотрудничества представляет собой рациональное (то есть равновесное) поведение, имеет теоретическое обоснование. Рассмотрим тот факт, что когда игроков спрашивают, почему они выбрали сотрудничество во время первых раундов игры, они обычно говорят нечто вроде: «Я был готов попробовать и посмотреть, насколько другой игрок благожелателен, а когда это оказывалось действительно так, я продолжал сотрудничать до тех пор, пока не приходило время воспользоваться его доброжелательностью». Безусловно, на самом деле другой игрок мог и не быть так дружественно настроен, но он мог размышлять аналогичным образом. Строгий анализ конечно повторяющейся дилеммы заключенных с подобной разновидностью асимметричной информации показывает, что в этом может заключаться еще одно ее решение. Если существует вероятность того, что участникам игры «дилемма заключенных» свойственна благожелательность, а не эгоизм, даже эгоистичному игроку может быть выгодно имитировать дружелюбие. Это позволит ему какое-то время получать более высокие выигрыши за счет сотрудничества, рассчитывая на то, что к концу последовательности раундов игры он воспользуется преимуществами обмана. Более подробный анализ ситуации, в которой только у одного из игроков есть выбор между дружественным и эгоистичным поведением, содержится в онлайн-приложении к данной главе. Решение соответствующей игры с двумя участниками представлено в оригинальной статье.
Кооперативное поведение в ходе лабораторных экспериментов можно объяснить, и не прибегая к такому типу асимметричности информации. Возможно, игроки не уверены, действительно ли отношения между ними будут разорваны в указанное время. Они могут считать, что их готовность к взаимодействию будет учтена в аналогичных играх против того же или других соперников. Не исключено, что они считают своих соперников наивными и в рамках проверки этой гипотезы готовы понести определенные убытки на протяжении пары раундов игры. В случае успеха этот эксперимент приведет к получению более высоких выигрышей в течение достаточно длительного периода.
В ходе ряда лабораторных экспериментов игроки участвуют в играх, состоящих из нескольких раундов, в каждом из которых выполняется конечное число повторений. Все повторные сеансы одного раунда разыгрываются против одного соперника, а каждый новый раунд — против нового соперника. Таким образом, в каждом раунде у игрока есть возможность наладить сотрудничество с соперником и накопить опыт для разработки стратегии против новых соперников в последующих раундах игры. Подобные ситуации показывают, что сотрудничество в начальных раундах игры длится дольше, чем в заключительных. Этот результат говорит о том, что теоретический вывод о прекращении сотрудничества, построенный на применении анализа методом обратных рассуждений, со временем формируется на основании опыта ведения игры, по мере того как игроки начинают лучше понимать выгоды и издержки своих действий. Еще одно возможное объяснение состоит в том, что игроки просто начинают понимать, что им необходимо первыми отказаться от сотрудничества, поэтому такой момент наступает все раньше по мере увеличения количества сыгранных раундов.
Предположим, вы участвуете в игре, структурированной как дилемма заключенных, и поддерживаете взаимодействие с другим игроком, но приближается известный вам момент его прекращения. Когда вам следует разорвать сотрудничество? Вы не должны делать это слишком рано, когда остается много потенциальных будущих выгод, но и не должны оставлять решение на слишком поздний этап игры, поскольку тогда ваш соперник может вас опередить и поставить перед фактом низкого выигрыша за тот период, когда он сам откажется от сотрудничества. Аналогичные расчеты применимы и в случае, когда вы поддерживаете конечно повторяющееся взаимодействие с неопределенным моментом его прекращения. Ваше решение об отказе от сотрудничества не может быть детерминированным, иначе ваш соперник понял бы это и опередил вас. Если детерминированное решение неосуществимо, то прекращение сотрудничества должно содержать элемент неопределенности (такой как смешанные стратегии) для обоих игроков. Во многих триллерах, сюжет которых основан на шатком сотрудничестве между преступниками или информаторами и полицией, напряженность присутствует именно по причине такой неопределенности.
Примеры прекращения сотрудничества между игроками по мере приближения повторяющейся игры к концу наблюдаются во многих ситуациях как в лабораториях, так и в реальном мире. Велогонки (или состязания в беге) — один из таких примеров. В течение большей части гонки игроки по очереди занимают лидирующую позицию и дают другим спортсменам возможность ехать в зоне пониженного давления. Однако по мере приближения к финишу каждый участник гонок делает стремительный рывок. По этой же причине весной в конце семестра в магазинах университетских городков появляются объявления «чеки не принимаются».
В ходе экспериментов на основе компьютерного моделирования был проанализирован целый диапазон стратегий (от очень простых до очень сложных), используемых игроками друг против друга в дилеммах заключенных с двумя участниками. Самый известный провел Роберт Аксельрод из Мичиганского университета. Он предложил всем желающим написать компьютерные программы, представляющие собой стратегии решения дилеммы заключенных, которая повторяется конечное, но достаточно большое количество раз (а именно 200 раз). Аксельрод получил 14 заявок, после чего организовал групповой турнир, в ходе которого пары программ соревновались друг с другом, в каждом случае выполняя по 200 повторных сеансов игры подряд. Во время турнира подсчитывались очки по всем парам во всех 200 повторных сеансах игры; на основании очков, набранных каждой программой в играх против всех остальных программ, была определена программа, получившая самый высокий результат. Для Аксельрода стало неожиданностью то, что «хорошие» программы показали самые высокие результаты; среди программ, занявших первых восемь мест в рейтинге, не было ни одной, которая бы когда-либо первой отказалась сотрудничать. Победила самая простая стратегия «око за око», представленная канадским специалистом по теории игр Анатолем Рапопортом. Программы, которые стремились к отказу от сотрудничества в любом отдельно взятом сеансе игры, сразу же получали выигрыш, но затем наступал период взаимных отказов и плохих выигрышей. Аксельрод объясняет успех стратегии равноценных ответных действий наличием четырех свойств: прощение, доброжелательность, возмездие и предсказуемость.
По мнению Аксельрода, в повторяющейся дилемме заключенных целесообразно придерживаться четырех простых правил: «Не завидовать. Не отказываться от сотрудничества первым. Отвечать на сотрудничество и отказ от него тем же. Не быть слишком умным». Стратегии «око за око» свойственны все четыре характеристики. В ней нет элемента зависти: ей не свойственно постоянное стремление превзойти конкурента, а все, что ей нужно, — это извлечь выгоду для себя. Кроме того, совершенно очевидно, что стратегия «око за око» следует совету не отказываться от сотрудничества первой и делает это только в ответ на действия соперника, всегда отвечая ему тем же. И наконец, для стратегии «око за око» нехарактерна чрезмерная сложность; она проста и понятна для соперника. На самом деле эта стратегия выиграла турнир не потому, что помогла игрокам получить высокие выигрыши в каждой отдельно взятой игре (состязание не сводилось к принципу «победитель получает все»), а потому, что всегда была близка к этому; она стимулирует сотрудничество и в то же время предотвращает эксплуатацию, тогда как другие стратегии неспособны на это.
После объявления результатов турнира Аксельрод предложил провести второй турнир. Его участникам была предоставлена возможность разработать программы, которые одержат победу над стратегией «око за око». Но в итоге она снова победила! Участвующие в турнире программы не смогли ее превзойти и показывали плохие результаты в противостоянии друг с другом. Аксельрод организовал также турнир иного рода. Вместо группы, в которой каждая программа играла против остальных программ только один раз, он провел игру с участием целой популяции программ, в которой было по несколько копий каждой программы. Программа каждого типа вступала в борьбу с соперником, выбранным из популяции случайным образом. Программы, которые добивались хороших результатов, получали более крупную долю в популяции, а доля программ с плохими результатами в популяции снижалась. Это была игра с элементами эволюции и естественного отбора, которую мы изучим более подробно в . В ее основе лежит простая идея, но ее результаты крайне интересны. Поначалу «плохие» программы добивались более весомых успехов за счет «хороших». Но по мере того как в популяции появлялось все больше «плохих» программ, они все чаще сталкивались друг с другом, поэтому их результативность начинала падать, а численность сокращаться. И вот тут стратегия «око за око» стала добиваться успеха и в итоге одержала победу.
Тем не менее у стратегии равноценных ответных действий есть свои недостатки. И главный — что она не допускает никаких ошибок при своей реализации. Если существует хотя бы малейший риск того, что игрок планировал сотрудничать, но по ошибке совершил действие, ориентированное на отказ от него, это может повлечь за собой целую серию аналогичных ответных действий, тем самым обрекая две программы «око за око» на плохой исход, а чтобы вырваться из этой последовательности, понадобится еще одна ошибка. Когда Аксельрод организовал третий турнир, в котором предусматривалась вероятность таких случайных ошибок, стратегию «око за око» сумели превзойти еще более благожелательные программы, которые допускали отдельные эпизоды отказа от сотрудничества, чтобы определить, ошибка это или системная попытка их эксплуатировать, и принимали ответные меры, только убедившись, что это не ошибка.
Любопытно, что в ходе турнира, организованного по аналогичной схеме в 2004 и 2005 годах в честь двадцатой годовщины турнира Аксельрода, победила новая стратегия. На самом деле это была группа стратегий, умеющих распознавать друг друга во время игры с тем, чтобы одна стратегия становилась сговорчивее под угрозой дальнейших отказов другой от сотрудничества. (Авторы сравнили свой подход с ситуацией, в которой заключенным удается обмениваться друг с другом информацией, перестукиваясь через стены камер.) Такой сговор означал, что некоторые стратегии, поданные победившей командой, показали очень плохие результаты, тогда как другие оказались весьма успешными, что стало подтверждением ценности сотрудничества. Разумеется, в турнире Аксельрода не допускалось участие нескольких программ, поэтому такие группы стратегий не соответствовали его правилам. Но участники недавнего турнира утверждают, что при отсутствии способа исключить координацию представленные ими стратегии могли бы одержать победу и в самом первом турнире.
6. Примеры дилеммы заключенных в реальном мире
Игры со структурой дилеммы заключенных присутствуют в неимоверном количестве различных контекстов в реальном мире. Хотя было бы неразумно пытаться вам показать каждый возможный случай возникновения такой дилеммы, все же мы воспользуемся представившимся моментом и детально проанализируем три конкретных примера из разных областей исследований. Один взят из эволюционной биологии, которую мы изучим более подробно в . Второй в качестве решения дилеммы заключенных описывает стратегию «гарантия лучшей цены». А третий касается международной политики в сфере охраны окружающей среды и способности повторяющегося взаимодействия смягчить дилемму заключенных в этой ситуации.
А. Эволюционная биология
В нашем первом примере мы рассмотрим игру под названием «дилемма шалашников». Как правило, самцы-шалашники привлекают самок, сооружая затейливые гнездовья — так называемые шалаши. Известно, что самки весьма разборчивы в выборе шалашей, построенных потенциальными партнерами, поэтому самцы часто отправляются на поиск шалашей соперников, чтобы их разрушить. Однако пока они выполняют эту миссию, их шалаш тоже может пострадать от клюва другого самца. Соперничество между самцами-шалашниками и стоящий перед ними выбор (грабить шалаш соперника или охранять свой) — это игра, имеющая структуру дилеммы заключенных. Орнитологи составили таблицу, в которой показаны выигрыши двух птиц с двумя возможными стратегиями — «грабить» или «охранять». В таблице выигрышей на рис. 10.8 комбинация ОО отображает преимущества стратегии «охранять», когда соперник также охраняет свой шалаш, а комбинация ОГ — выигрыш от охраны шалаша в случае, когда соперник — грабитель. Аналогичным образом комбинация ГГ отображает преимущества стратегии «грабить», когда соперник тоже грабитель, а комбинация ГО — выигрыш от ограбления чужого шалаша, когда соперник охраняет свое гнездо. Многолетние научные наблюдения за спариванием птиц позволили установить, что ГО > ГГ > ОО > ОГ. Другими словами, выигрыши в игре между шалашниками имеют в точности ту же структуру, что и в дилемме заключенных. Доминирующая стратегия птиц — «грабить», но когда ее выбирают обе птицы, это приводит к формированию равновесия, которое хуже для обоих, чем если бы оба применили стратегию «охранять».
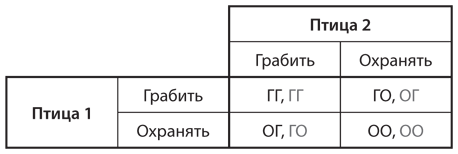
Рис. 10.8. Дилемма шалашников
В действительности стратегия, используемая любым шалашником, не результат процесса рационального выбора со стороны птицы. В эволюционных играх предполагается, что стратегии генетически запрограммированы в отдельных организмах, а выигрыши отображают репродуктивный успех разных типов. От того, какие равновесия формируются в подобных играх, зависит тип популяции, который могут наблюдать естествоиспытатели, например, это может быть популяция «грабителей», если доминирующая стратегия — «грабить», как на рис. 10.8. Однако, учитывая существование дилеммы, такой равновесный исход не самый лучший. При поиске решения дилеммы шалашников мы можем прибегнуть к повторяющемуся характеру взаимодействия в этой игре. В случае шалашников повторяющаяся игра против одного и того же или других соперников на протяжении нескольких сезонов спаривания может позволить вам, птице, выбрать гибкую стратегию на основе последнего хода соперника. Для решения подобной дилеммы в эволюционных играх могут использоваться (что часто и происходит) условные стратегии, такие как стратегия равноценных ответных действий. В мы вернемся к анализу эволюционных игр, их структуры и равновесных исходов.
Б. Гарантия лучшей цены
Теперь вернемся к игре в ценообразование и рассмотрим две компании, ведущие ценовую конкуренцию, используя одинаковые стратегии гарантии лучшей цены. Toys «R» Us и Kmart — национальные сети розничных магазинов, которые регулярно рекламируют цены на брендовые игрушки (и другие товары). Кроме того, обе компании официально объявили, что гарантированно компенсируют покупателям разницу между своей и рекламируемой ценой конкретного товара любого конкурента (модель и артикул товара должны быть идентичными), если покупатель предъявит его печатное рекламное объявление.
В этом примере будем исходить из того, что у компаний есть только два возможных варианта цен (низкая или высокая), которые они могут установить на определенную игрушку. К тому же мы используем гипотетические показатели прибыли и еще больше упростим анализ, предположив, что Toys «R» Us и Kmart — единственные конкуренты на рынке игрушек в определенном городе (например, в Биллингсе).
Допустим, базовая структура игры между двумя компаниями проиллюстрирована на рис. 10.9. Если обе компании будут рекламировать низкие цены, они поделят имеющийся потребительский спрос между собой и каждая получит 2500 долларов. Если обе будут рекламировать высокие цены, они поделят рынок с более низким объемом продаж, но их надбавки к цене будут достаточно большими для того, чтобы каждая компания могла заработать 3400 долларов. И наконец, если компании будут рекламировать разные цены, то у компании с высокой ценой вообще не будет покупателей и она ничего не заработает, а компания с низкой ценой получит 5000 долларов.
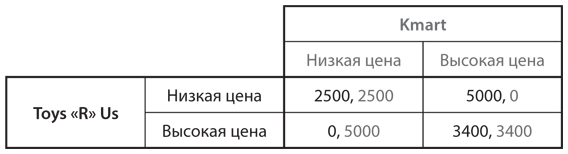
Рис. 10.9. Установление цен на игрушки в Toys «R» Us и Kmart
Очевидно, что игра, представленная на рис. 10.9, — это дилемма заключенных. Реклама и продажа товаров по низкой цене представляют собой доминирующую стратегию каждой компании, хотя обеим было бы выгоднее рекламировать и продавать игрушки по высокой цене. Но, как уже упоминалось ранее, фактически каждая компания использует третью стратегию — «гарантия лучшей цены», которую они предлагают покупателям. Как ее применение изменит дилемму заключенных, которая в противном случае возникла бы между компаниями?
Проанализируем, какие последствия повлечет за собой возможность выбирать между низкой, высокой и лучшей ценой. Стратегия «лучшая цена» сводится к следующему: компания рекламирует высокую цену, но обещает ее снизить до более низкой, которую предлагает конкурент. В таком случае компании, использующей эту стратегию, выгодно рекламировать высокую цену, если конкурент рекламирует низкую. Это подтверждает структура выигрышей в новой игре, представленной на рис. 10.10. В этой таблице мы видим, что ситуация, в которой одна компания выбирает стратегию «низкая цена», а другая — «высокая цена», эквивалентна выбору низкой цены обеими компаниями. В то же время если одна компания выбирает стратегию «высокая цена», а другая (или обе) — «лучшая цена», это эквивалентно применению обеими стратегии «высокая цена».
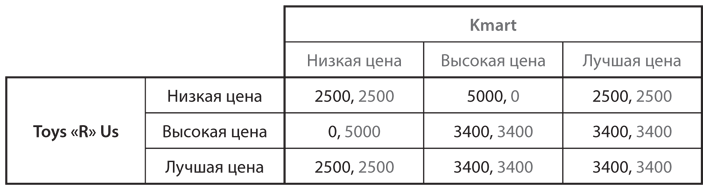
Рис. 10.10. Установление цен на игрушки в случае использования стратегии «лучшая цена»
Использование стандартных методов анализа игр с одновременными ходами показывает, что «высокая цена» слабо доминируется стратегией «лучшая цена» для обоих игроков и что после ее исключения стратегия «низкая цена» также становится слабо доминируемой стратегией «лучшая цена». Полученное в итоге равновесие Нэша подразумевает, что обе компании применят стратегию «лучшая цена» и обе заработают по 3400 долларов — уровень прибыли, эквивалентный тому, что компании получили бы при установлении высокой цены в исходной игре. Включение стратегии «лучшая цена» позволило игрокам найти выход из дилеммы заключенных, с которой они столкнулись, располагая только двумя простыми стратегиями — «низкая цена» и «высокая цена».
Как это произошло? Стратегия гарантии лучшей цены выступает в качестве механизма взыскания. Гарантируя такую же низкую цену, как и в Kmart, Toys «R» Us существенно снижает преимущества, которые получит Kmart за счет низкой цены на игрушки, в то время как Toys «R» Us устанавливает высокую цену. Кроме того, обещание предоставить такую же низкую цену, как и в Kmart, наносит вред и самой компании Toys «R» Us, поскольку ей придется смириться с низкой прибылью, полученной в связи со снижением цены. Следовательно, гарантия лучшей цены — это метод наказания обоих игроков в случае, если кто-то из них откажется от сотрудничества. Это в точности та же ситуация, что и в примере с мафией из , за исключением того, что сама схема наказания (а также более высокие цены, которые она поддерживает) используется на рынке практически во всех городах страны.
Реальные эмпирические данные о негативных последствиях такой политики ценообразования, хотя и в ограниченном количестве, существуют, а в ходе некоторых исследований были выявлены факты снижения цен на рынках, использующих эту стратегию. Однако результаты более поздних исследований все же подтверждают наличие сговора при применении компаниями стратегии «гарантия лучшей цены». Это должно насторожить всех покупателей. Даже если магазины, которые гарантируют лучшую цену, придерживаются данной стратегии во имя конкуренции, когда все компании начнут ее использовать, в конечном счете они смогут выиграть от этого больше, чем если бы не применяли эту стратегию вообще, а значит, в проигрыше могут оказаться именно покупатели.
В. Международная политика в сфере охраны окружающей среды: Киотский протокол
Наш последний пример связан с международным соглашением по контролю изменения климата, известным как Киотский протокол. Принятый в 1997 году как дополнительный документ к Рамочной конвенции ООН по вопросам изменения климата в качестве инструмента сокращения выбросов парниковых газов, он вступил в силу в 2005 году, а его первый этап завершился в 2012 году. Изначально договор подписали 170 стран, хотя следует отметить, что США среди них не было. Протокол был продлен едва ли не в последнюю минуту, в середине декабря 2012 года, и теперь действует до 2020 года.
Трудности с обеспечением глобального сокращения выбросов парниковых газов отчасти обусловлены тем, что взаимодействие между странами в этой области носит характер дилеммы заключенных. Любая отдельно взятая страна не заинтересована в сокращении собственных выбросов, зная, что, если сделает это в одиночку, то понесет существенные издержки без ощутимой пользы в плане общего изменения климата. Если другие страны все же сократят свои выбросы, первой стране нельзя будет помешать воспользоваться преимуществами предпринятых ими действий.
Проанализируем проблему сокращения выбросов парниковых газов в виде игры между двумя странами, Мы и Они. По данным британского департамента по вопросам изменения климата, скоординированные действия стран могут повлечь за собой издержки в размере 1% от ВВП страны, тогда как скоординированное бездействие может обойтись каждой стране в 5–20% от ВВП, возможно, в среднем по 12%. Следовательно, издержки одной страны в связи с сокращением выбросов могут достичь максимального значения в случае бездействия (20%), но если эта страна не станет сокращать выбросы и переложит выполнение этой задачи на другие страны, она не понесет практически никаких издержек. Мы можем представить ситуацию, сложившуюся между странами Мы и Они, в таблице 10.11, где выигрыши отображают изменение ВВП в каждой из стран.
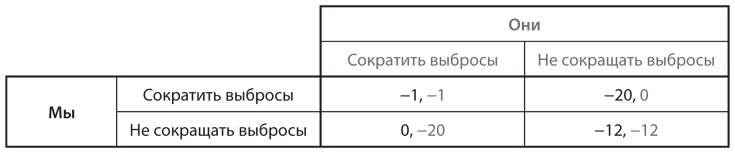
Рис. 10.11. Игра в сокращение выбросов парниковых газов
Игра, представленная на рис. 10.11, действительно представляет собой дилемму заключенных. Доминирующая стратегия каждой страны сводится к отказу от сокращения выбросов. Единственное равновесие Нэша наблюдается в случае, если ни одна страна не сокращает выбросов, но обе испытают на себе негативные последствия изменения климата. Исходя из этого анализа следовало бы ожидать, что в деле сокращения выбросов парниковых газов не будет достигнуто практически никакого прогресса.
Такую интерпретацию проблемы, присущей Киотскому протоколу, поставили под сомнение недавние исследования Майкла Либрайха, который утверждает, что эта игра не сводится к разовому взаимодействию и страны постоянно сотрудничают друг с другом и ведут переговоры о дополнительных поправках к действующему соглашению. По мнению Либрайха, итеративный характер игры позволяет решить ее с помощью условных стратегий и страны должны использовать стратегии, содержащие четыре важных элемента стратегии равноценных ответных действий, о которых говорил Аксельрод (см. ). В частности, странам целесообразно применять стратегии, обладающие следующими свойствами: доброжелательность (присоединение к протоколу и сокращение выбросов парниковых газов); возмездие (применение механизмов наказания по отношению к тем странам, которые не выполняют свою часть договоренностей); прощение (готовность приветствовать новые страны, присоединяющиеся к протоколу); предсказуемость (точное определение действий и ответных действий).
Либрайх оценивает действия нынешних игроков, таких как Евросоюз, Соединенные Штаты и развивающиеся страны (как одна группа), и дает ряд рекомендаций по улучшению ситуации. По его мнению, Евросоюз предпочитает доброжелательную, прощающую и предсказуемую стратегию, но не стратегию возмездия, поэтому другим странам выгодно отказаться от сотрудничества с Евросоюзом. Одним из возможных решений для Евросоюза может стать введение импортных пошлин, связанных с выбросами углекислого газа, или другой стратегии ответных действий во взаимодействии с несговорчивыми торговыми партнерами. Напротив, Соединенные Штаты Америки чаще придерживаются стратегии возмездия и прощения, учитывая их историю такого поведения после окончания холодной войны. Однако США не ведут себя доброжелательно или предсказуемо, во всяком случае на уровне всей страны (отдельные штаты могут придерживаться иной линии поведения), что дает другим странам стимул по возможности предпринимать против США быстрые и болезненные ответные меры. Решение о том, чтобы Соединенные Штаты взяли на себя серьезное обязательство по сокращению выбросов углекислого газа, — широко распространенный вывод во всех политических кругах. Развивающиеся страны Либрайх характеризует как недоброжелательные (они пытаются добиться того, чтобы на них не распространялись нормативы выброса углекислого газа), готовые прибегнуть к возмездию, непредсказуемые и не склонные к прощению. Либрайх утверждает, что таким странам, в частности Китаю, Индии и Бразилии, целесообразно примкнуть к международным инициативам по предотвращению изменения климата, что позволило бы им снизить риск возмездия и повысить шансы на извлечение выгоды из глобального улучшения климата на планете.
Общий вывод состоит в том, что процесс международного сокращения выбросов углекислого газа действительно соответствует профилю дилеммы заключенных. Тем не менее борьбу с выбросами парниковых газов нельзя рассматривать как бесперспективную лишь по той причине, что однократному взаимодействию между странами свойственны некоторые аспекты дилеммы заключенных. Повторяющееся взаимодействие между странами — участницами Киотского протокола делает возможным решение этой игры с помощью условных стратегий с такими свойствами, как доброжелательность, предсказуемость, прощение и возмездие.
Резюме
Дилемма заключенных — пожалуй, самая знаменитая стратегическая игра. Хотя у каждого игрока есть доминирующая стратегия («отказаться от сотрудничества»), равновесный исход менее благоприятен для игроков, чем в случае применения каждым из них доминируемой стратегии («сотрудничество»). Повторение игры — самое известное решение этой дилеммы. В конечно повторяющейся игре текущая стоимость будущего сотрудничества в итоге сводится к нулю, а анализ методом обратных рассуждений позволяет найти равновесие, в котором отсутствует кооперативное поведение. В бесконечно повторяющейся игре (или с неопределенным сроком окончания) сотрудничества можно достичь посредством применения подходящей условной стратегии, такой как стратегия равноценных ответных действий («око за око») или стратегия бесповоротного наказания; в любом случае сотрудничество возможно только тогда, когда его текущая стоимость превышает текущую стоимость отказа от него. В более общем плане перспектива того, что «завтра не наступит» (в случае краткосрочных отношений), приводит к уменьшению сотрудничества между игроками.
Дилемму заключенных можно также решить с помощью схем взыскания, которые позволяют изменить выигрыши игроков, отказывающихся от сотрудничества, когда их соперники его поддерживают или когда другие игроки также отказываются сотрудничать. Третий метод решения возникает в случае, когда издержки игрока в связи с отказом от сотрудничества превышают возможный выигрыш от его кооперативного поведения.
Экспериментальные данные свидетельствуют о том, что игроки зачастую сотрудничают дольше, чем предсказывает теория. Такое поведение объясняется неполнотой имеющихся у них знаний или их убеждениями в отношении преимуществ сотрудничества. В ходе экспериментов выяснилось, что стратегия равноценных ответных действий, обладающая такими свойствами, как предсказуемость, доброжелательность, возмездие и прощение, в среднем обеспечивает очень хорошие результаты в повторяющейся дилемме заключенных.
Дилеммы заключенных возникают в различных контекстах. Конкретные примеры из области международной экологической политики, эволюционной биологии и ценообразования показывают, как объяснить и спрогнозировать фактическое поведение посредством применения концепции дилеммы заключенных.
Ключевые термины
Бесконечный интервал
Взыскание
Коэффициент дисконтирования
Лидерство
Наказания
Повторяющаяся игра
Приведенная стоимость (PV)
Сложные проценты
Стратегия бесповоротного наказания
Стратегия равноценных ответных действий
Триггерные стратегии
Условные стратегии
Фактический коэффициент дисконтирования
Упражнения с решениями
S1. «Если дилемма заключенных повторяется 100 раз и оба игрока знают, сколько будет повторений, они непременно достигнут кооперативного исхода». Верно ли это? Обоснуйте свой ответ и приведите пример игры, которая его иллюстрирует.
S2. Рассмотрим игру с двумя участниками между Child’s Play и Kid’s Korner — производителями деревянных игровых комплексов для детей. Каждый игрок может установить либо высокую, либо низкую цену на стандартный игровой комплекс с двумя качелями и одной горкой. Если обе компании назначат высокую цену, прибыль каждой составит 64 000 долларов в год. Если одна компания установит низкую цену, а другая высокую, первая получит прибыль 72 000 в год, тогда как вторая — всего 20 000 долларов. Если обе компании назначат низкую цену, каждая получит по 57 000 долларов.
a) Убедитесь, что эта игра имеет структуру дилеммы заключенных, проанализировав выигрыши в случае разных комбинаций стратегий (обе компании выбирают сотрудничество, обе компании отказываются от сотрудничества, одна компания отказывается от сотрудничества и т. д.). Найдите стратегии и выигрыши в случае равновесия Нэша в этой игре с одновременными ходами, если игроки встречаются и принимают решения об установлении цен только один раз.
b) Если две компании решают сыграть в эту игру на протяжении фиксированного периода (скажем, 4 года), какой будет общая прибыль каждой из них к концу игры? (Не применяйте дисконтирование.) Объясните, как вы получили свой ответ.
c) Предположим, две компании постоянно играют в эту повторяющуюся игру. Пусть каждая из них использует стратегию бесповоротного наказания, в соответствии с которой обе назначают высокую цену до тех пор, пока одна не откажется от сотрудничества, и тогда обе компании установят низкую цену на весь оставшийся период. Какова однократная прибыль в результате отказа от сотрудничества в игре против соперника, использующего такую стратегию? Каковы убытки каждой компании за каждый будущий период в случае одного отказа от сотрудничества? Если r = 0, 25 (δ = 0,8), насколько целесообразно им сотрудничать? Определите диапазон значений r (или δ), при которых эта стратегия способна обеспечить сотрудничество между двумя компаниями.
d) Допустим, компании снова и снова год за годом играют в эту игру, не ожидая никаких изменений во взаимодействии друг с другом. Если бы мир перестал существовать через 4 года и ни одна из компаний не знала бы об этом заранее, какой была бы общая прибыль каждой из них (не дисконтированная) к концу игры? Сравните полученный ответ с ответом в пункте b. Объясните, почему они отличаются (если это действительно так) или почему одинаковые (если между ними нет различий).
e) Теперь представим, что две компании знают о наличии 10-процентной вероятности того, что одна из них может обанкротиться на протяжении любого года. Если банкротство действительно произойдет, повторяющаяся игра между компаниями закончится. Изменит ли знание этого факта действия компаний при r = 0, 25? Что если вероятность банкротства повысится до 35%?
S3. Каждое из двух подразделений компании возглавляет свой менеджер. Вознаграждение менеджеров зависит от количества усилий, которые они вкладывают в повышение производительности. Схема оплаты основана на сравнении результатов работы двух подразделений. Если оба менеджера выбирают высокий уровень усилий, каждый из них зарабатывает 150 000 долларов в год. Если оба предпочитают низкий уровень усилий, каждый получает «всего» 100 000 долларов в год. Однако если один из них выбирает высокий уровень усилий, а другой демонстрирует низкий, тогда первому заплатят 150 000 долларов плюс бонус 50 000 долларов, а второму — только урезанную заработную плату (за более низкую производительность по сравнению с конкурентом) в размере 80 000 долларов. Менеджеры принимают решения об уровне усилий независимо друг от друга, не зная о выборе соперника.
a) Постройте таблицу выигрышей для игры, в которой усилия, вкладываемые менеджерами в свою работу, не влекут за собой никаких издержек. Найдите в этой игре равновесие Нэша и объясните, можно ли ее назвать дилеммой заключенных.
b) Теперь предположим, что высокий уровень усилий требует от менеджеров определенных издержек (например, в связи с подачей дорогостоящего сигнала о качестве работы). В частности, представим, что он сопряжен с издержками в размере 60 000 долларов в год, которые несет менеджер, выбравший этот уровень. Составьте таблицу для новой версии игры и найдите равновесие Нэша. Объясните, будет ли эта игра дилеммой заключенных и чем она отличается от игры в пункте а.
c) Если издержки в связи с выбором высокого уровня усилий составляют 80 000 долларов в год, чем будет отличаться такая игра от игры в пункте b? Каким будет новое равновесие? Объясните, будет ли эта игра дилеммой заключенных и чем она отличается от игр в пунктах а и b.
S4. Вам необходимо решить, стоит ли инвестировать 100 долларов в предприятие друга, где через год эта сумма вырастет до 130 долларов. Вы с другом договорились, что он вернет вам 120 долларов, оставив 10 долларов себе. Но не исключено, что ваш друг может сбежать со всей суммой (130 долларов). Деньги, которые вы не инвестируете в предприятие друга, можно безопасно вложить куда-то еще под действующую ставку процента r и получить 100(1 + r) долларов в следующем году.
a) Постройте дерево игры для такой ситуации и покажите равновесие обратных рассуждений.
Теперь допустим, что игра повторяется бесконечное количество раз. То есть каждый год у вас есть возможность вложить еще 100 долларов в предприятие друга, и вы делите затем полученные 130 долларов по оговоренной выше схеме. Начиная со второго года вам предстоит принимать решение о целесообразности дальнейших инвестиций в предприятие друга, исходя из того, вернул он вам деньги за предыдущий год или нет. Процентная ставка между любыми двумя периодами подряд равна r — столько же, сколько и рыночная процентная ставка, и одинакова для вас и вашего друга.
b) При каких значениях r возможен равновесный исход в повторяющейся игре, в которой на протяжении каждого периода вы вкладываете деньги в предприятие друга и он выплачивает вам деньги в соответствии с договоренностью?
c) Если процентная ставка составляет 10% в год, существует ли альтернативная договоренность о разделении прибыли, представляющая собой равновесный исход бесконечно повторяющейся игры, в которой в каждом периоде вы инвестируете средства в предприятие друга и он выплачивает вам деньги в соответствии с договоренностью?
S5. Вернитесь к примеру из , в котором заработная плата менеджеров двух подразделений компании зависит от выбора ими высокого или низкого уровня усилий, которые они вкладывают в работу. В сказано, что издержки в связи с выбором высокого уровня усилий составляют 60 000 долларов. Теперь допустим, что оба менеджера многократно ведут игру, представленную в , на протяжении многих лет. Такое повторение делает возможным особый тип сотрудничества, при котором один из менеджеров выбирает высокий уровень усилий, тогда как другой — низкий. При этом оба заключают соглашение о сотрудничестве, в соответствии с которым менеджер, выбирающий высокий уровень усилий, выплачивает второму менеджеру дополнительные суммы с тем, чтобы оба получили одинаковые выигрыши.
a) Какой размер дополнительного платежа гарантирует, что окончательные выигрыши двух менеджеров будут одинаковыми? Сколько каждый менеджер заработает за тот год, в течение которого будет действовать соглашение о сотрудничестве?
b) Сотрудничество в этой повторяющейся игре подразумевает выбор каждым менеджером предписанного уровня усилий и соответствующие дополнительные платежи менеджера с высоким уровнем менеджеру с низким. При каких значениях процентной ставки такое соглашение может поддерживать между ними сотрудничество в повторяющейся игре?
S6. Рассмотрим , с несколько более общими выигрышами (на k = 1).
Предположим, это повторяющаяся игра, которая проводится каждую субботу вечером. Если k < 1, двум игрокам выгодно постоянно взаимодействовать, выбирая стратегии «свернуть» / «свернуть», тогда как при k > 1 им выгодно сотрудничать в случае, если один их них применит стратегию «свернуть», а другой — «ехать прямо», каждую неделю по очереди выбирая стратегию «ехать прямо». Может ли любой из этих двух типов сотрудничества быть устойчивым?
S7. Вспомните игру из , где Южная Корея и Япония конкурируют на рынке производства танкеров класса VLCC. Как и в пунктах а и b этого упражнения, стоимость строительства судов составляет 30 миллионов долларов в каждой стране, а спрос на танкеры равен P = 180 – Q, где Q = qКорея + qЯпония.
a) Ранее мы нашли равновесие Нэша в этой игре. Теперь найдите исход, основанный на сговоре. Какое общее количество танкеров должны производить обе страны, чтобы максимизировать свою прибыль?
b) Предположим, две страны выпускают одинаковое количество танкеров класса VLCC, а значит, имеют равную долю в прибыли, полученной в случае сговора. Какую прибыль получит каждая страна? Сравните ее с прибылью, которую бы они имели в случае равновесия Нэша.
c) Теперь давайте допустим, что две страны поддерживают повторяющееся взаимодействие. Один раз в год они определяют объем производства, и каждая страна располагает информацией о том, сколько танкеров выпустил конкурент за прошлый год. Обе страны хотят сотрудничать ради получения прибыли, вычисленной в пункте b. На протяжении любого отдельно взятого года каждая из стран может нарушить условия соглашения. Если одна из них сохранит количество выпущенных танкеров на оговоренном уровне, какое количество танкеров лучше всего построить другой стране? Какую прибыль в итоге получат они обе?
d) Составьте матрицу выигрышей этой игры, представив ее в виде дилеммы заключенных.
e) При каких значениях процентной ставки возможно поддержание сговора в случае, если две страны используют стратегию бесповоротного наказания, которая сводится к отказу от сотрудничества навсегда?
Упражнения без решений
U1. Два человека, Бейкер и Катлер, играют в игру, в которой выбирают и делят приз. Бейкер решает, каким будет общий размер приза, 10 или 100 долларов. Катлер выбирает, как разделить приз, выбранный Бейкером: либо поровну, либо в неравных частях; тогда он получит 90 процентов, а Бейкер 10. Составьте таблицу выигрышей в этой игре и найдите ее равновесия для каждой из следующих ситуаций.
a) Ходы делаются одновременно.
b) Бейкер ходит первым.
c) Катлер ходит первым.
d) Является ли эта игра дилеммой заключенных? Почему да или почему нет?
U2. Рассмотрим небольшой городок, жители которого очень любят пиццу, но в нем можно разместить только две пиццерии, Deep Dish Донны и Pizza Pies Пирса. Каждый торговец должен выбрать цену на свою пиццу, но для простоты предположим, что доступны только две цены: высокая и низкая. При высокой цене торговцы могут получить прибыль 12 долларов на одну пиццу, при низкой — 10 долларов. У каждой пиццерии есть круг лояльных клиентов, которые покупают 3000 штук пиццы в неделю независимо от назначенной пиццерией цены. Существует также плавающий спрос в размере 4000 пицц в неделю. Но их покупатели чувствительны к ценам и пойдут в заведение с более низкой ценой. Если обе пиццерии установят одинаковую цену, они разделят этот спрос пополам.
a) Составьте таблицу выигрышей для этой игры в ценообразование между пиццериями, воспользовавшись прибылью каждой пиццерии за неделю (в тысячах долларов). Найдите в игре равновесие Нэша и объясните, почему это дилемма заключенных.
b) Теперь предположим, что у Deep Dish Донны гораздо больше лояльных клиентов, которые гарантированно покупают 11 000 (а не 3000) пицц в неделю. Размер прибыли и уровень плавающего спроса остаются теми же. Составьте таблицу выигрышей в новой версии игры и найдите равновесие Нэша.
c) Как наличие более крупной базы лояльных клиентов у Deep Dish «решает» дилемму, возникшую у этих двух пиццерий?
U3. Городской совет состоит из трех членов, которые ежегодно голосуют за повышение собственной заработной платы. Для принятия такого решения требуются два голоса «за». Каждый член совета хотел бы повышения, но при этом ему выгоднее голосовать против, поскольку это бонус в глазах избирателей. Выигрыши каждого члена городского совета таковы:
решение о повышении принято, свой голос «против»: 10;
решение о повышении не принято, свой голос «против»: 5;
решение о повышении принято, свой голос «за»: 4;
решение о повышении не принято, свой голос «за»: 0.
Все три члена городского совета голосуют одновременно. Составьте трехмерную таблицу выигрышей и покажите, что в случае равновесия Нэша решение о повышении заработной платы не может быть единогласным. Проанализируйте, как повторяющееся взаимодействие между членами совета может обеспечивать им ежегодное повышение заработной платы, если 1) каждый член совета занимает эту должность на протяжении трех лет; 2) каждый год в рамках ротации один из них должен быть переизбран; 3) у горожан короткая память, поэтому они помнят результаты голосования о повышении заработной платы членов городского совета только за прошлый, но не за предыдущие годы.
U4. Рассмотрим игру, которую проводит нейтральный судья, разработанную Джеймсом Андреони и Хэлом Вэрианом из Мичиганского университета. В ней участвуют два игрока — Строка и Столбец. Судья дает каждому из них две карточки: 2 и 7 Строке и 4 и 8 Столбцу. Эта информация доступна всем участникам игры. Затем игрокам, играющим одновременно и независимо друг от друга, предлагают отдать судье карточку либо с большим, либо с меньшим числом. Судья раздает выигрыши в долларах (взятых из общего фонда, а не из кармана игроков), размер которых зависит от того, какие карточки он собирает. Если Строка выберет карточку с меньшим числом 2, ее выигрыш составит 2 доллара; если Строка отдаст карточку с большим числом 7, тогда Столбец получит 7 долларов. Если Столбец отдаст карточку с меньшим числом 4, то он получает 4 доллара; если Столбец выберет карточку с большим числом 8, то Строка получит 8 долларов. Выигрыши от других вариантов сочетаний карточек показаны в таблице выигрышей.
a) Покажите, что полная таблица выигрышей в этой игре выглядит следующим образом.
b) Найдите равновесие Нэша в этой игре. Определите, будет ли она дилеммой заключенных.
Теперь предположим, что игра состоит из следующих этапов. Судья раздает карточки, как и раньше, и информация о них известна всем. На этапе 1 каждый игрок из собственного кармана может выделить определенную сумму, которая будет храниться у судьи на счете условного депонирования; сумма может быть нулевой, но не отрицательной. Когда оба игрока сделают выбор на этапе 1, эта информация обнародуется. Далее на этапе 2 оба игрока снова выбирают карточки одновременно и независимо друг от друга. Судья раздает выигрыши из общего фонда, как и в случае одноэтапной игры. Кроме того, он распоряжается средствами, находящимися на счете условного депонирования, следующим образом. Если Столбец выберет карточку с большим числом, судья отдаст ему сумму, которую дала на хранение Строка; если Столбец выберет карточку с меньшим значением, выделенная Строкой сумма вернется к ней. Сумма, которую внес на счет условного депонирования Столбец, распределяется по аналогичному принципу, в зависимости от того, какую карточку выберет Строка. Эти правила известны всем участникам игры.
c) Найдите равновесие обратных рассуждений (совершенное равновесие подыгры) в этой двухэтапной игре. Решает ли оно дилемму заключенных? Какова роль счета условного депонирования?
U5. Компании Glassworks и Clearsmooth конкурируют на местном рынке ремонта ветровых стекол. Размер рынка (общий объем прибыли этих компаний) составляет 10 миллионов долларов в год. Каждая компания решает, размещать ли ей рекламу на местном телевидении. Если компания решит размещать рекламу в том или ином году, это обойдется ей в 3 миллиона долларов. Если одна компания разместит рекламу, а другая нет, то первая захватит весь рынок. Если рекламу разместят обе компании, они поделят рынок поровну. Если обе решат не размещать рекламу, они также поделят рынок поровну.
a) Допустим, обе компании знают, что будут конкурировать всего один год. Составьте матрицу выигрышей в этой игре. Найдите стратегии, образующие равновесие Нэша.
b) Предположим, компании играют в эту игру пять лет подряд и знают, что к концу пятилетнего периода обе планируют выйти из бизнеса. Найдите совершенное равновесие подыгры в этой игре из пяти периодов. Обоснуйте свой ответ.
c) В чем состояла бы стратегия «око за око» в игре, описанной в пункте b?
d) Представим, что компании будут играть в эту игру неопределенное время и что их будущая прибыль дисконтируется по ставке 20% в год. Можете ли вы найти совершенное равновесие подыгры, обеспечивающее более высокие годовые выигрыши, чем равновесие, найденное в пункте b? Если да, объясните, какие стратегии в него входят. Если нет, обоснуйте свой вывод.
U6. Вернитесь к пиццериям Deep Dish Донны и Pizza Pies Пирса, о которых шла речь в упражнении U2. Предположим, они не ограничены выбором из двух возможных цен и могут выбрать конкретное значение цены, обеспечивающей максимальную прибыль. Допустим также, что приготовление одной пиццы обходится в 3 доллара (в каждой пиццерии), а опыт или результаты изучения рынка показали наличие такой зависимости между объемом продаж (Q) и ценой (P):
QПирс = 12 – PПирс + 0,5PДонна .
Тогда прибыль каждой компании за неделю (Y, в тысячах долларов) составит:
YПирс = (PПирс – 3)QПирс = (PПирс – 3)(12 – PПирс + 0,5PДонна),
YДонна = (PДонна – 3)QДонна = (PДонна – 3)(12 – PДонна + 0,5PПирс).
a) С помощью этих функций прибыли определите правило наилучших ответов каждой компании, как показано в , и используйте эти правила для поиска равновесия Нэша в данной игре. Какие цены выберут компании в случае равновесия? Какую прибыль получит каждая компания за неделю?
b) Если компании поддерживают сотрудничество и выбирают общую наилучшую цену P, то прибыль каждой компании составит:
YДонна = YПирс = (P – 3)(12 – P + 0,5P) = (P – 3)(12 – 0,5P).
Какую цену выберут компании, чтобы максимизировать общую прибыль?
c) Представим, что две пиццерии поддерживают повторяющееся взаимодействие, пытаясь сохранить рассчитанные в пункте b общие цены, максимизирующие прибыль. Они печатают новое меню каждый месяц, тем самым связывая себя обязательствами на весь этот период. На протяжении любого месяца одна из компаний может отказаться от этих обязательств. Если одна пиццерия сохранит цену на согласованном уровне, при какой цене другой выгоднее отказаться от дальнейшего сотрудничества? Какую прибыль получат обе пиццерии в итоге? При каких значениях процентной ставки сговор между ними будет устойчивым благодаря стратегии бесповоротного наказания?
U7. Давайте расширим анализ, представленный в , допустив возможность отказа от сотрудничества в триополии, построенной на сговоре. В мы нашли основанный на равновесии Нэша исход игры в случае триополии на рынке производства танкеров класса VLCC, в состав которой входят Корея, Япония и Китай.
a) Теперь найдите исход этой игры, основанный на сговоре. То есть определите, какое количество танкеров VLCC должны выпускать три страны, чтобы обеспечить максимальную общую прибыль.
b) Предположим, в случае построенного на сговоре исхода игры, найденного в пункте а, эти три страны производят равное количество танкеров VLCC, а значит, каждая из них получает равную долю в общей прибыли. Какой будет прибыль каждой страны? Сравните ее с объемом прибыли, которую получит каждая страна в случае равновесия Нэша.
c) Теперь представим, что эти страны поддерживают повторяющееся взаимодействие. Один раз в год они определяют объем производства, причем каждая страна знает, сколько танкеров выпустили конкуренты в предыдущем году. Эти страны хотят сотрудничать, чтобы получать основанные на сговоре уровни прибыли, рассчитанные в пункте b. На протяжении любого года одна из стран может нарушить соглашение. Если две другие страны, как предполагается, должны обеспечить свою долю предусмотренного сговором результата, вычисленного в пунктах а и b, то какое количество танкеров лучше всего построить стране, отказавшейся от дальнейшего сотрудничества? Какую прибыль она в итоге получит, если выпустит оптимальное количество танкеров, тогда как две другие страны произведут столько, сколько было оговорено?
d) Безусловно, через год после отказа одной из стран от дальнейшего сотрудничества оба ее конкурента также его прекратят. Все три страны вернутся к исходу, основанному на равновесии Нэша (навсегда, в случае применения стратегии бесповоротного наказания). Какой выигрыш получит страна, переставшая сотрудничать с конкурентами, за один год отказа от основанного на сговоре исхода? Какие убытки понесет за каждый последующий год страна, отказавшаяся от сотрудничества, в связи с получением прибыли согласно равновесию Нэша, вместо прибыли, предусмотренной сговором?
e) При каких значениях процентной ставки сговор между тремя странами будет устойчивым благодаря стратегии бесповоротного наказания? Они выше или ниже значений, найденных в случае дуополии в ? Почему?

