Книга: Электроника для начинающих (2-е издание)
Назад: Эксперимент 8. Генератор на основе реле
Дальше: Эксперимент 10. Транзисторные переключатели
Эксперимент 9. Время и конденсаторы
Электроны перемещаются практически со скоростью света, но мы, тем не менее, можем с их помощью измерять время в секундах, минутах или даже в часах. Описанный далее эксперимент покажет вам, как это сделать.
Что вам понадобится
• Макетная плата, монтажный провод, кусачки, инструмент снятия изоляции, тестовые провода, мультиметр
• Батарея 9 В и разъем (1 шт.)
• Кнопки (2 шт.)
• Обычный светодиод (1 шт.)
• Резисторы на 470 Ом, 1 кОм, 10 кОм (по 1 шт.)
• Конденсаторы емкостью 0,1 мкФ, 1 мкФ, 10 мкФ, 100 мкФ, 1000 мкФ (по 1 шт.)
Заряд конденсатора
Вначале настройте мультиметр на измерение постоянного напряжения в вольтах и измерьте разность потенциалов на клеммах 9-вольтовой батареи. Если оно меньше 9,2 В, то для этого эксперимента придется взять свежую батарею.
Установите на макетную плату две кнопки, резистор номиналом 1 кОм и конденсатор емкостью 1000 мкФ, как показано на рис. 2.75. С помощью тестовых проводов подключите мультиметр так, чтобы вы могли измерить напряжение на выводах конденсатора и при этом ваши руки оставались свободными.
Присоедините разъем к батарее и вставьте питающие провода в крайние отверстия, соединенные с двумя шинами макетной платы, расположив положительный провод слева, как показано на рис. 2.75.
Если мультиметр показывает больше, чем 0,1 В, разрядите конденсатор, нажав кнопку В, которая накоротко замкнет обе обкладки конденсатора.
После этого нажмите кнопку А и засеките на часах, будильнике или смартфоне, за сколько секунд конденсатор зарядится до напряжения 9 В. Если у вас мультиметр с автоматическим выбором диапазона, он должен сам переключиться с начального значения в милливольтах на вольты по мере увеличения заряда. Когда я проводил этот эксперимент, измерение заняло чуть более трех секунд.
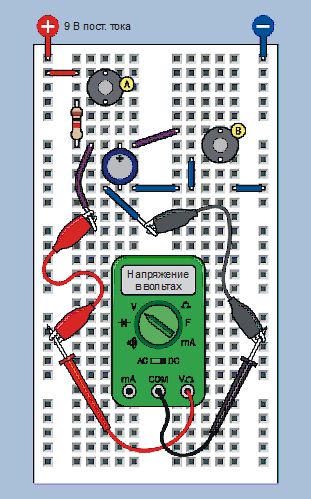
Рис. 2.75. Простая установка для измерения времени заряда конденсатора. Емкость конденсатора равна 1000 мкФ, номинал резистора — 1 кОм
На рис. 2.76 изображена схема описанного устройства, которая поможет вам понять, как все работает.
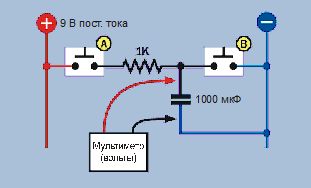
Рис. 2.76. Электрическая схема установки, изображенной на рис. 2.75
Положительная обкладка конденсатора стала «более положительной», а его отрицательная обкладка стала «более отрицательной», поскольку положительные и отрицательные заряды притягиваются друг к другу на пластинах конденсатора. Разность потенциалов на выводах конденсатора возросла, хотя ток через него не проходит. Одно из первых утверждений, которые вы встретите при чтении популярных книг по электронике, гласит: конденсатор не пропускает постоянный ток.
Пока вы подаете на конденсатор неизменный во времени электрический потенциал, это утверждение остается верным.
Резистивно-емкостная цепочка
Выньте резистор 1 кОм и замените его резистором 10 кОм. Если мультиметр показывает вам, что на конденсаторе есть остаточное напряжение, разрядите его, нажав кнопку В. После этого повторите тест. Зафиксируйте, насколько долго конденсатор заряжается до 9 В через резистор номиналом 10 кОм.
Описанное простое сочетание конденсатора и резистора называется резистивно-емкостной цепочкой (или RC-цепочкой, R — резистор, С — конденсатор). Это очень важное понятие в электронике. Прежде чем я объясню, что она делает, вот несколько вопросов для размышления:
• Точно ли в 10 раз дольше заряжался конденсатор до напряжения 9 В при замене резистора номиналом 1 кОм на резистор 10 кОм?
• Постоянной ли была скорость роста напряжения на конденсаторе или же оно увеличивалось быстрее в начале эксперимента (или, наоборот, ближе к окончанию)?
• Как вы считаете, если подождать достаточно долго, сможет ли напряжение на конденсаторе достичь напряжения батареи?
Напряжение, сопротивление и емкость
Представьте, что резистор — это вентиль, ограничивающий поток воды, а конденсатор — это резиновый шарик, который вы пытаетесь наполнить (рис. 2.77). Если вы закроете вентиль до такой степени, что вода просачивается по каплям, шарик будет заполняться очень долго. Но небольшой поток воды все же может наполнить емкость, если вы подождете достаточно долго. Если предположить, что шарик не лопнет, процесс закончится, когда давление внутри шарика сравняется с давлением воды в трубе, которая подает воду через вентиль.
Но здесь упущен из виду один важный фактор. По мере того как шарик наполняется, оболочка растягивается, оказывая большее давление на его содержимое. С увеличением давления внутри шарика оно выталкивает входящий поток воды. Следовательно, мы можем ожидать, что с течением времени вода будет заполнять резервуар все медленнее.
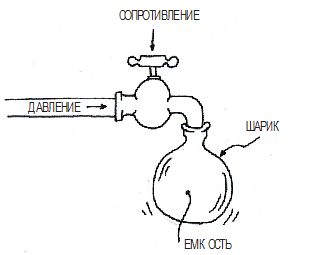
Рис. 2.77. Воду, наполняющую резиновый шарик, можно сравнить с поступающими в конденсатор электронами
Как это соотносится с электронами, стремящимися в конденсатор? Концепция аналогична. Сначала электроны стремительно поступают, но по мере заполнения пространства новоприбывшим требуется больше времени на поиск свободного места. Процесс заряда становится все медленнее и медленнее. На самом деле, напряжение на конденсаторе теоретически никогда не сравняется с подаваемым на него напряжением.
Постоянная времени
Скорость, с которой заряжается конденсатор, зависит от параметра, известного как «постоянная времени». Определение очень простое:
ТС = R × С
Здесь ТС — постоянная времени, в секундах, если конденсатор с номиналом С (измеряемым в фарадах) заряжается через резистор с номиналом R (в омах).
Вернемся к схеме, которую вы тестировали вначале, используя резистор номиналом 1 кОм. Можно подставить номиналы компонентов в формулу для постоянной времени, только при этом следует перевести единицы измерения в омы и фарады. Так, 1 кОм равен 1000 Ом, а 1000 мкФ — это 0,001 фарада. Поэтому получить результат проще простого:
ТС = 1000 × 0,001
Следовательно, для таких номиналов резистора и конденсатора ТС = 1 с.
Но что означает полученный результат? Значит ли это, что конденсатор будет заряжен полностью за одну секунду? К сожалению, не все так просто.
На самом деле постоянная времени ТС — это время (в секундах), необходимое конденсатору для того, чтобы напряжение на нем составило 63% от подаваемого напряжения, если заряд начался с нулевого напряжения.
А что если конденсатор заряжается не с нуля? Если мы начинаем измерения после того как конденсатор уже приобрел некоторое напряжение, определение становится немного сложнее. Если VDIF — это разность между напряжением конденсатора и подаваемым напряжением, то ТС — это интервал времени (в секундах), необходимый для добавления 63% величины VDIF к его текущему значению.
ЗамечаниеПочему 63%? Почему не 62? Или 64? Или 50? Ответ на этот вопрос слишком сложен для данной книги, и вам придется почитать о постоянных времени где-либо еще, если вы захотите узнать больше. Приготовьтесь к изучению дифференциальных уравнений.
Для простоты используем такую аналогию. На рис. 2.78 вы видите лакомку, которому достался вкусный торт. Вначале наш гурман очень голоден, и поэтому он отрезает 63% от торта и съедает этот кусок за одну секунду — это его «постоянная времени» поедания торта. Во второй заход он берет 63% от оставшегося торта; а поскольку он уже не настолько голоден, ему требуется еще одна секунда (помните о том, что это его постоянная времени). В третий раз он опять отрезает 63% от остатка и снова поедает его за секунду. И так далее. Желудок постепенно наполняется тортом, подобно тому, как конденсатор наполняется электронами. Но он никогда не съест весь торт, потому что всегда берет только 63% от остатка.
На рис. 2.79 этот процесс показан еще одним способом. По истечении каждой константы времени (которая равна 1 секунде, если у нас конденсатор емкостью 1000 мкФ и резистор 1 кОм) конденсатор получает 63% разности между текущим напряжением и напряжением, подаваемым от источника питания.
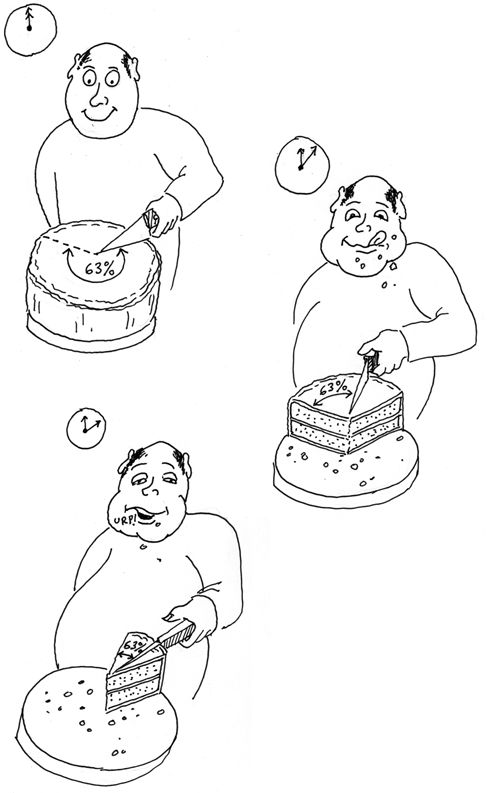
Рис. 2.78. Если съедать только 63% торта, оставшегося на тарелке, то желудок наполняется так же, как заряжается конденсатор. Не имеет значения, как долго будет продолжаться трапеза, — торт никогда не кончится, а желудок никогда не будет полностью заполнен
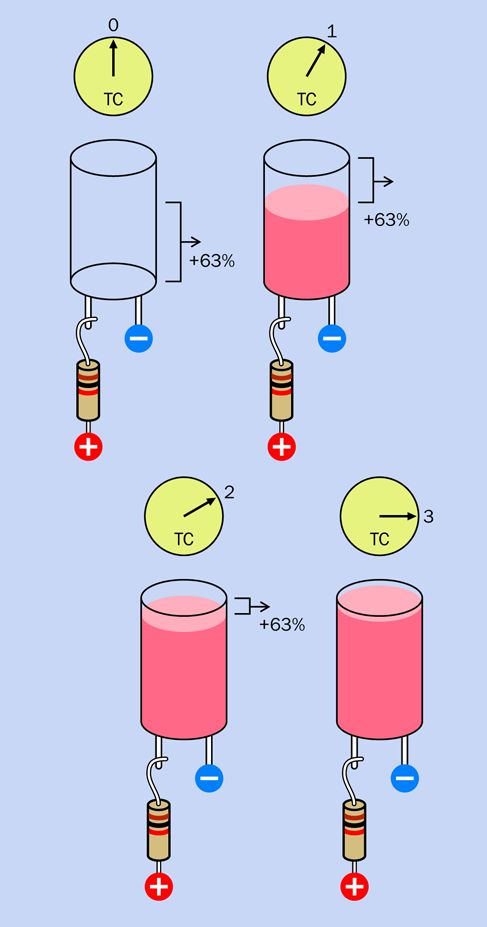
Рис. 2.79. Другой взгляд на процесс заряда конденсатора
В мире идеальных компонентов процесс заряда будет продолжаться бесконечно. Но в реальных условиях мы считаем, что по истечении временного интервала, равного пяти постоянным времени, заряд конденсатора приблизится к 100%, и можно считать процесс завершенным.
График заряда конденсатора
Мне хотелось бы начертить график, показывающий напряжение на обкладках конденсатора по мере его заряда. Чтобы сделать это, я рассчитаю необходимые значения с помощью формулы для постоянной времени.
Предположим, VCAP — это напряжение на конденсаторе в данный момент, a VDIF — разность между текущим напряжением на конденсаторе и напряжением питающей батареи. Приведенная далее формула даст ответ на вопрос, каким будет новое напряжение конденсатора по прошествии одной постоянной времени. Обозначим это новое напряжение как VNEW. Формула выглядит следующим образом:
Величина 0,63 означает то же, что и 63%.
Предположим, батарея выдает ровно 9 В, а конденсатор начал заряжаться с нулевого напряжения. Итак, VCAP = 0, a VDIF = 9. Подставим эти значения в формулу:
VNEW = 0 + (0,63 × 9)
Расчет на калькуляторе дает 0,63 × 9 = 5,67. Поэтому по истечении одной постоянной времени (одной секунды с резистором номиналом 1 кОм и конденсатором емкостью 1000 мкФ) на конденсаторе будет напряжение 5,67 В.
А что будет в следующую секунду? Необходимо повторить вычисления, подставив новые значения. Теперь текущее напряжение конденсатора, VCAP, равно 5,67. Батарея по-прежнему выдает 9 В, поэтому значение VDIF = 9 - 5,67 = 3,33. Подставим эти значения в ту же формулу:
VNEW = 5,67 + (0, 63 × 3,33)
Калькулятор подсказывает, что произведение 0,63 на 3,33 составляет около 2,1. А 2,1 плюс 5,67 даст 7,77. Значит, после второй секунды напряжение на конденсаторе будет равно 7,77 В.
Многократно повторив аналогичные вычисления, получим последовательность чисел, подобную приведенной далее (с округлением до сотых). Значения будут соответствовать напряжению на конденсаторе в конце каждой секунды, при условии что напряжение источника питания равно 9 В:
После 1 секунды: 5,67 ВПосле 2 секунды: 7,77 ВПосле 3 секунды: 8,54 ВПосле 4 секунды: 8,83 ВПосле 5 секунды: 8,94 ВПосле б секунды: 8,98 В
График на рис. 2.80 был получен путем построения гладкой кривой через эти расчетные точки. Наибольшее значение по оси абсцисс составляет 6 секунд, поскольку при этом напряжение на конденсаторе вплотную приблизилось к 9 В.
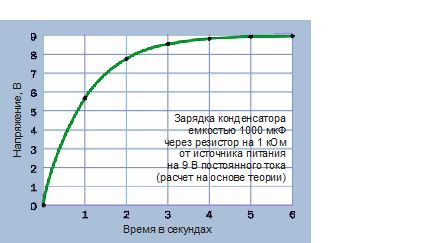
Рис. 2.80. График иллюстрирует процесс заряда конденсатора с течением времени
Экспериментальное подтверждение
В предыдущем разделе я рассказал вам, как рассчитать напряжение на конденсаторе при его заряде через резистор. Но как подтвердить, что я прав? Должны ли вы верить мне на слово?
Возможно, вы захотите проверить все самостоятельно. Другими словами, необходимо экспериментальное подтверждение, которое является важной частью процесса «Изучения через открытия».
Вернитесь к нашей предыдущей схеме и убедитесь, что номинал резистора равен 10 кОм, а не 1 кОм. Попросите кого-нибудь сесть рядом с вами, чтобы следить за временем, пока вы наблюдаете за дисплеем вашего мультиметра, показывающим значение в вольтах. Каждые 10 секунд ваш помощник подает команду, и вы в этот момент записываете показания мультиметра. Выполняйте все это в течение минуты.
Поскольку у вас резистор 10 кОм, а не 1 кОм, постоянная времени теперь составляет 10 секунд, а не одну. Поэтому ваши показания должны выглядеть как ряд напряжений, который я привел ранее с интервалами в 1 секунду (см. рис. 2.80), но теперь интервалы будут 10-секундными.
Ваши значения напряжения должны быть близки к моим, но не будут совпадать в точности. Почему? Есть множество причин.
• Ваша батарея не обеспечивает такое же напряжение, что и моя.
• Номинал вашего резистора не равен в точности 10 000 Ом.
• Емкость вашего конденсатора не точно 1000 микрофарад.
• Ваш мультиметр имеет погрешность.
• Вам требуется несколько микросекунд, чтобы снять показания мультиметра.
• Ваш помощник мог давать команду не в точности каждые 10 секунд.
Есть еще два фактора, о которых я не упомянул. Во-первых, конденсаторы сохраняют электрический заряд не идеально. Они обладают утечкой, из-за которой заряд постепенно убывает. Это происходит даже тогда, когда конденсатор набирает заряд. Ближе к концу процесса заряда электроны перетекают так медленно, что утечка (скорость, с которой они уходят обратно) становится существенной в сравнении с зарядкой.
Кроме того, ваш мультиметр имеет некоторое внутреннее сопротивление. Оно очень большое, но все же не бесконечное. Это значит, что мультиметр «крадет» небольшое количество заряда от конденсатора, пока вы измеряете напряжение. Да, сам процесс проведения измерений изменяет значение, которое вы пытаетесь определить! Это, на самом деле, очень распространенная проблема в физике и инженерном деле.
Я могу представить способы минимизации всех перечисленных факторов, но не знаю средства, позволяющего устранить их полностью. Всегда будет присутствовать некоторая экспериментальная погрешность. И ее приходится учитывать, когда вы проводите эксперимент, чтобы подтвердить теорию. Подтверждение может быть очень долгим процессом, требующим значительного терпения — именно поэтому теоретиками являются, как правило, одни люди, а экспериментаторами — совсем другие.
Емкостная связь
Теперь, когда я рассказал вам о том, как конденсаторы заряжаются и разряжаются, вернемся к ранее сделанному утверждению: «конденсатор не пропускает постоянный ток».
Возможно, вы помните, что я также сказал «пока вы подаете на конденсатор неизменный во времени электрический потенциал, это утверждение остается верным».
Но что если этот электрический потенциал будет меняться? Что происходит в тот момент, когда конденсатор переходит из состояния отсутствия заряда к внезапному подключению источника напряжения? Что ж, это совсем другое дело. В этих условиях электрический сигнал способен пройти через конденсатор.
Как такое возможно? Обкладки внутри конденсатора не касаются друг друга, как же тогда электрический импульс может перескочить с одной на другую? Вскоре мы разберемся с «как» и «почему». Но сначала вам необходимо убедиться в том, что описываемое мною происходит на самом деле.
Взгляните на компоненты макетной платы, показанной на рис. 2.81. Эта компоновка подобна схеме на рис. 2.75, но резистор номиналом 10 кОм переместился с левой стороны на правую, а также появился светодиод и резистор 470 Ом.
На рис. 2.82 изображена электрическая схема устройства с рис. 2.81, которая поможет прояснить ситуацию.
И чтобы не возникло недоразумений, на рис. 2.83 я указал все компоненты и обозначил их номиналы.
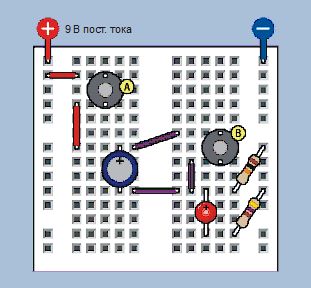
Рис. 2.81. Мигание красного светодиода демонстрирует работу конденсатора при быстрой смене напряжения
После того как вы соберете схему, вначале не забудьте нажать кнопку В, чтобы разрядить конденсатор. Затем нажмите кнопку А. Подумайте, почему светодиод вспыхнул и медленно погас?
Нажмите кнопку А снова. На этот раз почти ничего не происходит. Очевидно, что перед началом работы конденсатор должен быть в разряженном состоянии. Поэтому нажмите кнопку В, чтобы разрядить его. Теперь опять нажмите кнопку А, и светодиод загорится снова.
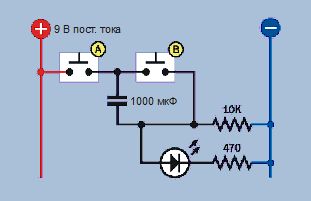
Рис. 2.82. Схема устройства, изображенного на рис. 2.81
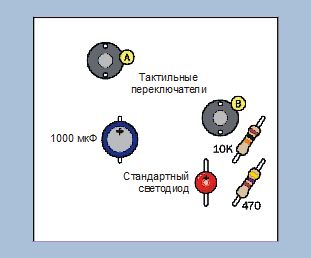
Рис. 2.83. Компоненты на макетной плате
Мы знаем, что в исходном состоянии напряжение на конденсаторе практически отсутствовало, поскольку он был подключен к отрицательному заземлению через резистор 10 кОм. Кроме того, перед началом эксперимента, нажав кнопку В, вы замкнули обе обкладки конденсатора между собой. (Вот почему я просил вас разрядить его.)
Затем вы нажимаете кнопку А, которая мгновенно подает на одну из обкладок положительный импульс, одновременно зажигается светодиод, соединенный с другой обкладкой. Ток, проходящий через светодиод, должен был откуда-то взяться, и единственное объяснение состоит в том, что он поступает от конденсатора.
Ток смещения
Давайте попробуем повторить эксперимент, подключив вместо светодиода и резистора мультиметр. На рис. 2.85 показана компоновка макетной платы, а на рис. 2.84 — электрическая схема. Разрядите конденсатор, нажав кнопку В, а затем снимите показание мультиметра. Оно должно быть около нуля вольт.
При нажатии кнопки А следите за мультиметром очень внимательно. Цифровой прибор реагирует не сразу, но вы все же увидите резкое увеличение напряжения и его последующее постепенное уменьшение.
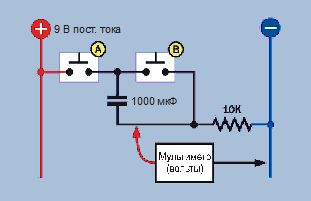
Рис. 2.84. Схема для измерения тока смещения
Когда я подключил к этой схеме осциллограф, который может измерять и отображать очень быстрые изменения напряжения, сигнал был похож на кривую, которую я добавил в нижней части рис. 2.85. Увеличение напряжения было таким быстрым, что казалось мгновенным.
То, что ток, протекающий через конденсатор, может изменяться практически мгновенно, хорошо известно и это часто используется в электронике. Но как такое возможно?
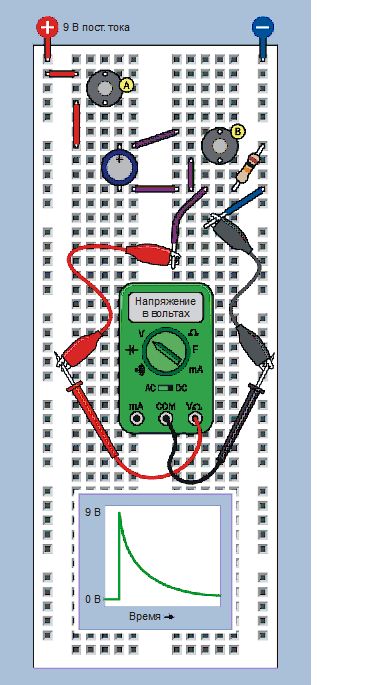
Рис. 2.85. Вместо светодиода с резистором в этой установке включен мультиметр
Этот вопрос заинтересовал первого экспериментатора, Джеймса Максвелла, который считал, что так быть не должно; поэтому он разработал теорию и придумал выражение для описания увиденного. Он назвал данное явление током смещения. Это соответствовало некоторым теориям, которые он разрабатывал в то время.
Сегодня есть и другие теории. Очевидно, что бросок тока резко меняет электрическое поле внутри конденсатора, и этот эффект может навести напряжение на противоположной обкладке. На самом деле все происходит гораздо сложнее, но в большинстве популярных книг просто говорится что-то вроде «конденсатор не пропускает постоянный ток, но пропустит колебания напряжения».
Если вы возьмете конденсатор меньшей емкости, то увидите, что он пропускает более короткий импульс. Уберите мультиметр и верните светодиод и резистор 470 Ом обратно в схему, а затем попробуйте использовать конденсаторы емкостью 100 мкФ, 10 мкФ, 1 мкФ и 0,1 мкФ. В последних экспериментах мигание светодиода вряд ли будет заметно.
Переменный ток
Если вы соберете предыдущую схему (см. рис. 2.84), но измените полярность питающего напряжения, она по-прежнему будет работать, хотя ток потечет в противоположном направлении (рис. 2.86). На рис. 2.87 показана экспериментальная установка, где резистор 10 кОм перемещен влево, а кнопка А — вправо. Мультиметр по-прежнему измеряет напряжение в точке между резистором и конденсатором. В схеме на рис. 2.86 отображена эта модификация устройства.
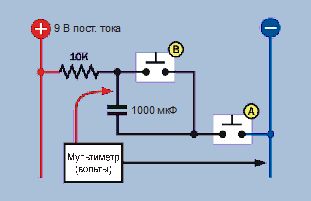
Рис. 2.86. Электрическая схема устройства, изображенного на рис. 2.87
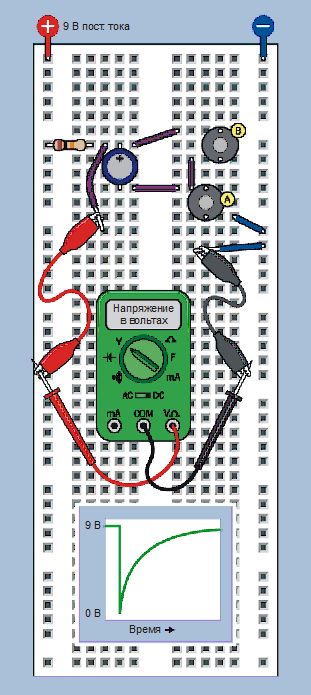
Рис. 2.87. Полярность подачи питания изменена на обратную
После того как вы нажмете и отпустите кнопку В, чтобы разрядить конденсатор, мультиметр покажет значение напряжения около 9 В, потому что верхний вывод конденсатора подключен к положительной шине через резистор номиналом 10 кОм. Конденсатор не пропускает постоянный ток, и поэтому создается впечатление, что его сопротивление бесконечно, а положительному заряду «некуда идти». На рис. 2.88 показано, как увеличивается напряжение между двумя резисторами, когда растет сопротивление между этой точкой и заземлением.
Тем не менее, когда вы нажимаете кнопку А в вашей установке на макетной плате, это создает отрицательный импульс. Эффективное сопротивление конденсатора на некоторое время исчезает, пока проходит импульс, в результате чего показания мультиметра снизятся. Затем конденсатор медленно перезаряжается, как это было в предыдущем опыте. Кривая, изображенная внизу на рис. 2.87, демонстрирует общее представление о том, как изменяется заряд конденсатора.
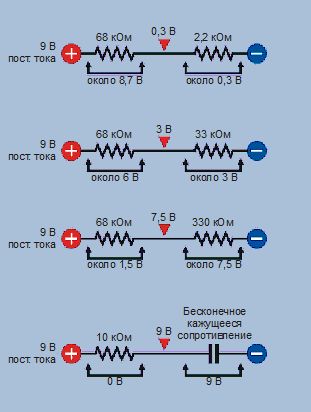
Рис. 2.88. Когда у вас два последовательно соединенных резистора и левый из них подключен к источнику питания, а правый к отрицательному заземлению, то напряжение между ними увеличивается по мере роста номинала правого резистора
Подведем итог:
• Конденсатор не пропускает постоянный ток.
• Тот же конденсатор пропускает быстрые колебания напряжения, независимо от направления тока.
• Кроме того, конденсатор накапливает электрический заряд.
Это приводит к важному заключению. Поскольку переменный ток — это быстрая серия относительно отрицательных и относительно положительных импульсов, конденсатор позволяет им проходить через него.
Емкость конденсатора будет иметь большое значение. Когда вы используете малые номиналы, вы увидите, что они будут срабатывать быстро. Менее емкие конденсаторы будут пропускать высокочастотные колебания и блокировать низкочастотные — такое поведение очень полезно во многих областях применения, в том числе при работе с аудиосигналами. Вы убедитесь в этом сами в эксперименте 29. Учитывайте то, что звуковые сигналы являются разновидностью переменного тока, поскольку их амплитуда меняется очень быстро.
Когда конденсатор служит для пропускания переменного тока и блокирования постоянного, мы называем его разделителънъш конденсатором. Он обеспечивает передачу переменного сигнала из одной части схемы в другую, но блокирует напряжение постоянного тока, которое может существенно отличаться. Я продемонстрирую это свойство, когда мы доберемся до эксперимента 11.

