Случайность также зарекомендовала себя как мощное оружие в борьбе с проблемами дискретной оптимизации, такими как создание расписания баскетбольных матчей NCAA или поиск кратчайшего маршрута для коммивояжера. В предыдущей главе мы увидели, как релаксация помогает снизить количество подобных проблем, но тактическое использование случайности стало, возможно, даже более значимым способом.

Представьте себе, что вы планируете путешествовать по миру и посетить десять городов. Ваша собственная версия проблемы коммивояжера: вы улетаете и прилетаете в Сан-Франциско и планируете побывать в Сиэтле, Лос-Анджелесе, Нью-Йорке, Буэнос-Айресе, Лондоне, Амстердаме, Копенгагене, Стамбуле, Дели и Киото. Вас не слишком волнует общая протяженность маршрута, но вы, вероятно, стремитесь снизить расходы на поездку. Первое, что стоит здесь отметить: хотя десять городов – это не так уж и много, но количество возможных вариантов маршрута – это 10! (10 факториал) – более 3,5 млн. Иными словами, у вас нет никакой практической возможности проверить каждую комбинацию и выбрать самую низкую цену. Придется получше пораскинуть мозгами.

В качестве первой попытки построить маршрут вы можете рассмотреть самый дешевый рейс из Сан-Франциско (скажем, в Сиэтл), а затем найти самый дешевый рейс оттуда в любой из оставшихся городов (пусть это будет Лос-Анджелес), потом самый дешевый оттуда (например, в Нью-Йорк) и т. д., пока вы не дойдете до десятого города, откуда вам нужно будет лететь обратно в Сан-Франциско. Это пример так называемого жадного алгоритма, который можно еще назвать близоруким: на каждом этапе пути он близоруко выбирает лучший вариант из тех, что под рукой. В теории планирования, которую мы рассмотрели в главе 5, жадный алгоритм – например, выполнение самой простой и занимающей меньше всего времени работы из доступных, не заглядывая далеко вперед, – порой может стать именно тем, что требуется для решения проблемы. В этом случае решение проблемы коммивояжера, которое может предложить жадный алгоритм, не самое плохое, но далекое от лучшего из возможных.

После того как вы построили базовый маршрут, вам стоит проверить возможные альтернативы, меняя последовательность городов, и посмотреть, получается ли лучше. Например, если мы решили сперва лететь в Сиэтл, а потом в Лос-Анджелес, можно попробовать поменять их местами: сначала Лос-Анджелес, затем Сиэтл. Для любого заданного маршрута мы, таким образом, можем переставить местами два города 11 раз. Скажем, мы перепробуем все варианты и выберем тот, который позволит нам максимально сэкономить. С этого момента у нас есть новый построенный маршрут, с которым мы будем работать дальше, и мы можем снова заняться перестановкой, чтобы извлечь какие-то дополнительные выгоды. Этот алгоритм называется «восхождение на холм», поскольку поиск лучших и худших решений среди множества вариантов можно рассматривать как путешествие по холмистой местности с целью взобраться на самую высокую гору.

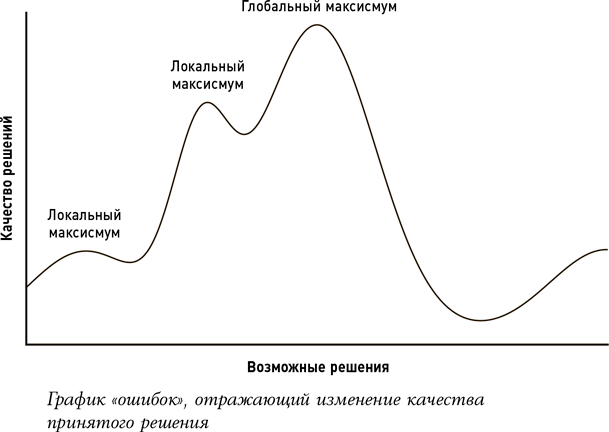
В конечном итоге вы найдете наилучшее решение из всех возможных перестановок. И не важно, какие соседние города вы меняете местами: оно останется таковым. Именно здесь заканчивается ваше восхождение на холм. Означает ли это, что вы нашли единственно возможный наилучший маршрут? К сожалению, нет. Вы могли найти только так называемый локальный максимум, но не глобальный максимум всех вероятностей. Холмистый ландшафт к тому же окутан туманом. Вы можете сделать вывод, что стоите на вершине холма, только на основе того факта, что вокруг вас видны уходящие вниз склоны. Но, возможно, за долиной есть гора и повыше, скрытая за облаками.

Представьте себе лобстера, застрявшего в ловушке: бедное животное не понимает, что для того, чтобы выбраться, ему нужно вернуться к центру клетки, то есть забраться в нее поглубже. Ловушка для лобстеров не что иное, как локальный максимум из проволоки – локальный максимум, который убивает.

В ситуации с планированием отпуска локальные максимумы, к счастью, не столь фатальны, но несут в себе тот же смысл. Даже если нам удастся найти решение, которое нельзя будет улучшить за счет мелких ухищрений, вполне вероятно, что мы по-прежнему упускаем глобальный максимум. Истинно наилучший маршрут может потребовать полного изменения плана всей поездки: придется, к примеру, поменять местами целые континенты или направляться с востока на запад, а не с запада на восток. Нам порой приходится временно ухудшить наш вариант, если мы хотим продолжать искать лучший. И случайность обеспечивает стратегию для этого – несколько стратегий, если быть точным.