Чешский иллюзионист Зденек Брадак попал в Книгу рекордов Гиннесса, установив рекорд по сортировке колоды карт. 15 мая 2008 года Брадак смог разложить в правильном порядке колоду из 52 карт всего за 36,16 секунды. Как ему это удалось? Какую технику сортировки он применял? И хотя его ответ, очевидно, пролил бы свет на теорию сортировки, сам Брадак воздержался от комментария. Мы, несомненно, уважаем мастерство и ловкость маэстро, но при этом мы на 100 % уверены, что можем побить его рекорд. По сути, мы уверены на 100 %, что можем поставить рекорд, который никто не сможет побить. Все, что нам нужно, – это около 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 824 000 000 000 000 попыток в борьбе за звание рекордсмена. Это число, значение которого немного больше 80 унвигинтиллионов (52 факториал, или 52! в математическом обозначении), – число возможных перестановок в колоде карт. Предпринимая такое количество попыток, вы рано или поздно обязательно сложите колоду в правильном порядке, при этом абсолютно случайно. Таким образом, теперь мы можем с гордостью вписать в Книгу рекордов Гиннесса имя Кристиана Гриффитса, выступившего с не таким уж и плохим временем – 0 минут 0 секунд. По правде говоря, таким способом мы бы точно пытались установить новый рекорд до конца света. Тем не менее этот факт явно указывает на огромные фундаментальные различия между рекордсменами и учеными-компьютерщиками. Именитые господа из Книги рекордов Гиннесса беспокоятся только о показателях в наилучшем случае. Конечно, едва ли их можно винить за это, ведь все спортивные рекорды – не что иное, как показатели одного лучшего выступления. Однако информатику практически никогда не волнует наилучший случай. Вместо этого ученые хотели бы знать, сколько в среднем занимает тасование карт у того же Брадака: было бы здорово заставить его тасовать колоду все 80 унвигинтиллионов раз (или что-то в этом роде) и оценивать его по средней скорости на протяжении всех попыток (теперь вы понимаете, почему программистов не допускают до таких вещей).

Более того, специалисту по информатике было бы интересно узнать и наихудшее время при тасовании колоды. Анализ наихудшего случая позволяет нам получить четкие гарантии, что процесс в принципе конечен, что срок исполнения задачи не будет сорван.

Таким образом, до конца этой главы, да и, пожалуй, всей книги мы будем обсуждать действие алгоритмов в наихудших случаях, если не указано иное.

В программировании есть обозначение, придуманное специально для определения сценария алгоритма в наихудшем случае. Это прописная «О», или «О большое». За понятием «О большого» стоит одна небольшая хитрость, которая с первого взгляда не совсем очевидна. Суть в том, что «О большое» не столько выражает действие алгоритма в минутах и секундах, сколько может характеризовать тип взаимосвязи между размером задачи и временем, потраченным на ее решение. Поскольку «О большое» намеренно проливает свет на некоторые важные детали, перед нами появляется схема разделения задач на различные широкие категории.

Представьте, что вы организуете ужин с друзьями, количество которых мы обозначим как n. Время, которое вам необходимо на уборку дома до их прихода, не зависит от n.

Это самая простая категория задач, которая называется «О большое от единицы» (обозначается как «О(1)») и также известна как временнáя константа. Примечательно, что для «О большого» абсолютно не важно, сколько времени у вас на самом деле занимает уборка. Главное – что временной промежуток всегда один и тот же, вне зависимости от списка гостей. От вас требуется выполнить одну и ту же работу, не важно, пригласили вы одного друга, десять, сто или любое другое количество.

Теперь время, которое займет передача жаркого вокруг стола, мы обозначим как «О большое от n» (письменно – «O(n)»). Это понятие также имеет другое название – «линейное время». Если количество гостей увеличивается в два раза, то же происходит и с линейным временем. И снова, для «О большого» безразлично, какое количество блюд вы подаете или, например, сколько раз гости попросят добавки. В каждом случае время линейно зависит от количества приглашенных гостей и график зависимости времени от количества гостей будет представлять собой прямую. Более того, существование любых линейно-временных факторов – в случае «О большого» – будет перекрывать все факторы временных констант.

Другими словами, «передача жаркого вокруг стола» и «передача жаркого вокруг стола после трехмесячной перепланировки вашей столовой» – для программиста, по сути, абсолютно равнозначные величины.

Если вам это кажется безумным, подумайте о том, что компьютеры работают с величинами n, которые могут исчисляться тысячами, миллионами или миллиардами. Иначе говоря, программисты мыслят очень, очень большими объемами данных. Если у вас миллион гостей, то по сравнению с единичной передачей блюда вокруг стола весь процесс перепланировки дома покажется вам ничтожным.

А что если каждый прибывающий гость будет обнимать остальных при приветствии? Ваш первый гость обнимет только вас, второму придется обнять уже двоих, третий гость обнимет уже троих. Сколько объятий случится за вечер?

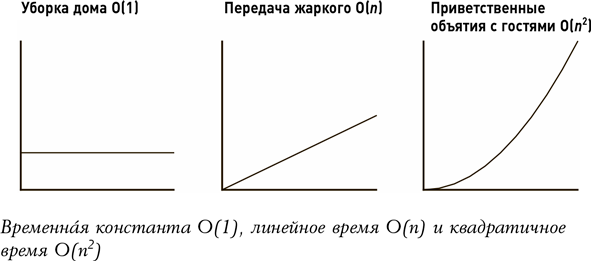
Эта задача перейдет уже в разряд «О большое от n в квадрате» («О(n2)»), или квадратичного времени. Опять же для нас важны только общие черты связей между переменной n и временем. Не существует формулы O(2n2) для двух объятий на каждого или формулы O(n2 + n) для объятий и передачи блюда. Таким образом, O(n2) охватывает все процессы.

Вот здесь становится трудно, потому что появляется экспоненциальное время, которое рассчитывается по формуле O(2n), когда каждый дополнительный гость удваивает вашу работу. Еще сложней все обстоит с факториальным временем, определяемым по формуле O(n!). Это категория задач столь бесчеловечно трудных, что программисты упоминают их только в шутку (как мы, говоря, например, о сортировке колоды до победного конца) или когда им на самом деле очень-очень хотелось бы пошутить.