Гармония и числа: рациональные числа и иррациональные отношения

ВСЁ ЕСТЬ ЧИСЛО!

Пифагор

Я не учу мудрости, я исцеляю от невежества.

Пифагор

В соответствии с главной доктриной Пифагора «всё есть число» познание гармонии Мироздания, изучение и описание гармонии вещей и явлений началось с математической точки зрения и инструментами математики. Появилось направление, названное «математика гармонии», основу которого заложили работы Пифагора, Платона и Евклида. В развитии математики гармонии в течение двух с половиной тысяч лет принимали активное участие выдающиеся мыслители и учёные: Фибоначчи, Пачоли, Кеплер, Кассини, Бине, Люка, Клейн и др. Тайна и концепция гармонии, поиск и выявление математических соотношений и пропорций, баланс вещей, числовых последовательностей, уравнений, построение гармоничных геометрических фигур и форм – предмет исследований, вдохновения и практического применения учёных и мыслителей с древнейших времён до наших дней. Наиболее известные направления исследований гармоний – Платоновы тела Куба Метатрона, золотое сечение, числа Фибоначчи. Одной из главных книг, описавших математику гармонии, являются «Начала» Евклида. В этом величайшем математическом сочинении даны понятия о рациональных числах и иррациональных величинах, геометрическая теория пяти Платоновых тел, золотого сечения. Проникновение этих знаний и идей во все сферы деятельности человека и современной науки от естествознания до информатики – закономерность и основа гармоничного развития цивилизации, стимул развития, безопасность и красота.

Математика со своего зарождения решала две проблемы: проблему счёта и проблему измерения, что привело к формированию двух фундаментальных математических понятий. Проблема счёта сформировала понятие натуральных (рациональных или соизмеримых) чисел, а решение проблемы измерения «несоизмеримых отрезков», измерения величин, которые не могут быть точно выражены ни целым числом, ни дробью, привело к такому понятию, как иррациональные (несоизмеримые) числа. Более точным определением категории иррациональных чисел будет слово «величина». Для счёта использовались рациональные числа, для выражения гармонии и отношений – иррациональные. Рациональные числа являются дискретными и могут меняться лишь «прыжками» от одного числа к соседнему: например, с 1 на 2. Фундаментальная суть иррациональных чисел состоит в том, что они непрерывны и бесконечны. Ещё до нашей эры пифагорейцы называли их не числами, а величинами и относили к классу сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени, – сущностей, которые могут меняться непрерывно. Позже Евдокс Книдский (ок. 408 г. до н. э. – ок. 355 г. н. э.) развил теорию пропорций как рациональных, так и иррациональных отношений, обосновав, что нет никакой необходимости называть иррациональную величину числом, так как это несоизмеримая величина и её нельзя сопоставить с количественным значением. Классификация и исследование иррациональных величин описаны в «Началах» Евклида, классическом и фундаментальном труде древности, заложившем основу для изучения рациональных, иррациональных чисел и правильных многоугольников – Платоновых тел.

Два понятия – натуральные (рациональные) и иррациональные числа – лежат в основании математики. Исходя из фундаментальной сути двух видов чисел: дискретных рациональных чисел и непрерывных, бесконечных иррациональных величин, – в наше время их можно рассмотреть с позиции квантовой механики, в которой объект квантового микромира является при одних условиях волной, а при других частицей, и только в момент наблюдения происходит коллапс (редукция) волновой функции и фиксация квантового объекта в определённой форме – волны или частицы. Аналогия классификации математических чисел с представлениями квантовой механики очень простая. Частицу условно можно сравнить с простым рациональным числом и определить как Рацио, так как она локальна и дискретна. Волна соответствует понятию иррационального числа, она бесконечна и непрерывна – Иррацио. Некоторые интерпретаторы квантовой механики считают, что именно сознание наблюдателя, следовательно, и его выбор определяют состояние объекта в момент наблюдения – будет ли это частица или волна, Рацио или Иррацио. Таким образом, получается, что человек, и, следовательно, его сознание как часть личности, и все объекты информации, осознаваемые им, – это структура одновременно дискретная и бесконечная, рациональное и иррациональное, волна и частица.

Это два описания состояния и два отображения одного предмета исследования, они равны, равнозначны и характеризуют единое целое с двух сторон. Каждый объект информации, даже макрообъект, можно рассмотреть как микроквантовый, то есть как частицу или волну, как рациональное число и иррациональную величину. В соответствии с некоторыми физическими представлениями квантовой механики, предложенными Эрвином Шрёдингером в работе «Избранные труды по квантовой механике», нет разницы между микромиром, живущим по квантовым законам, и макромиром, наблюдаемым нами, или разницы может не быть и наш видимый мир живёт по тем же законам, что и квантовые (малые) микрочастицы: электроны, фотоны, кванты, корпускулы, лептоны. И именно сознание наблюдателя создаёт реальность, коллапсируя постоянно волновые функции квантовых состояний системы. В связи с возникновением квантовой механики нельзя более поддерживать представление о существовании в Мире объективной реальности вне объекта наблюдения, в отрыве от самого наблюдателя. Субъект и объект неотделимы друг от друга.

Рациональное число представляет статику бесконечного количества рациональных чисел, дискретный фрагмент вечности целого, а иррациональное число представляет само целое и неизмеримое, содержащее внутри все дискретные объекты.

У иррациональных чисел есть два основных свойства: они вычислимы, то есть конкретны, и в то же время бесконечны, то есть их можно вычислять бесконечно до любой степени точности, до любого значащего знака, и состоят они из неповторяющихся фрагментов. А бесконечное иррациональное число можно исчислять тоже бесконечно, и только в момент остановки вычисления оно будет зафиксировано в том конкретном виде и до того знака точности, до которого дошёл математик (наблюдатель) или вычислительная машина, исполняя программу расчёта. Любая произвольная последовательность цифр обязательно когда-нибудь встретится в бесконечном иррациональном числе.

Так как любую информацию можно представить в виде числа, то любое иррациональное арифметическое число содержит всё, весь Мир, весь объём информации обо всей Вселенной и вне её. То есть в любом иррациональном числе можно найти любую информацию о любом объекте, следовательно, можно и получить ответ на любой вопрос как настоящего, так прошлого и будущего, будущего во всех его вариантах, причём все эти варианты истинные и равноправные (равнозначные). Именно поэтому иррациональные числа в наибольшей степени соответствуют тому, что принято называть Хаосом. Это бесконечный потенциал воплощения конкретной реальности.

Таким образом, Мир можно описать и представить в виде рациональных чисел и иррациональных величин, которые содержат в себе числовое выражение любого объекта Мира и его взаимосвязей с другими объектами, а значит, и всего Мира в целом в любой момент его развития.

Иррациональное число не может быть выражено никаким доступным рациональным числом или рациональной дискретной величиной, оно является скрытым и тайным до завершения момента вычисления, но, так как оно бесконечно и вычислять его можно вечно, познаваться оно также будет вечно, сохраняя покров тайны своей полноценности. Любое иррациональное число непрерывно, но в то же время вычитаемо и определено в момент вычисления, и оно цельно и неизменно по своей структуре. То есть любые повторные вычисления всегда дадут тот же самый вариант до остановки вычисления на конкретной позиции. Это определяет устойчивость Мира и невозможность уничтожения информации, так как она существует в любом иррациональном числе, которое цельно и неизменно, значит, информацию можно найти на том же моменте вычисления, где она была изначально создана. Следовательно, Мир всегда можно восстановить через иррациональные методы взаимодействия и через всеобщие связи. Таким образом, информация не может быть уничтожена, она может быть только потеряна для восприятия сознанием конкретного человека или коллективным сознанием общества, и задачей является её нахождение в бесконечности иррациональных систем и величин Мира.

Числовой ряд – это рациональное число, соответствующее направленной цели взаимодействия, выбранной человеком лично. Это всегда конкретное натуральное рациональное число. У числового ряда есть своя информационная область. Концентрация на числовом ряде – это и есть способ более точного попадания в эту область. Числовой ряд нормирования позволяет получать такое духовное состояние, которое соответствует норме структур и взаимосвязей человека и окружающего Мира. Но любой объект реальности существует одновременно в двух своих состояниях – рациональной и иррациональной, он может быть проявлен и как частица, и как волна. Связь с иррациональной областью действия достигается путём рисования в свободной форме, привязанной к выбранному числу. В свободной форме – значит любыми линиями, цветом и способом, любым инструментом, который именно в момент рисования нравится человеку. Говоря иначе, такими действиями устанавливается духовное состояние, причём это духовное состояние должно соответствовать норме как человека, так и окружающего Мира. Но поскольку понятие духа ассоциируется с движением и волной, более точным с научной точки зрения будет говорить об иррациональных величинах (отношениях) и их гармонии.

Гармоничные отношения всегда измеряются иррациональными величинами, самый известный пример гармонии – золотое сечение. Многие обожествляют гармонию золотого сечения, часто образно говорят, что она воплощает животворящий дух, что это формула мироздания. Важно осознать, что гармония действительно есть, её всегда можно увидеть и почувствовать в любой работе, что чувства и отношения могут и должны быть гармоничными. Следовательно, это состояние достижимо, к нему надо стремиться в каждом своём действии, и ЧИСЛОГРАФИКА открывает путь к достижению такого гармоничного состояния, синхронизируя рациональную и иррациональную структуры сознания человека.

Гармония пропорций и отношений в форме, звуке, цвете, в развитии и строении может быть выражена через числа в предельно точном виде. Отношения форм друг к другу, их гармоничные пропорции и есть состояние нормы, и эту гармонию можно выразить через число. Недаром существует устойчивое выражение «гармоничные отношения». Эти гармоничные отношения выражают через иррациональные числа – иррациональные величины. Эти иррациональные числа могут передать всё, как форму (геометрия), так и волну – взаимодействие или движение волны в геометрической форме. Форма существует не только сама по себе как идеальная абстрактная идея или как конкретный объект реальности. Это сосуд для работы волны – света (цвета) и звука, так как через форму, через пространство, имеющее форму, проходит свет. Волна может распространяться и идти только в пространственной форме. Каждая форма влияет на оптику, рассеивает или фокусирует свет, и гармоничная форма нормирует и пространство, и свет, а значит, и жизнь.

Числа могут обозначать геометрию, выражать характеристику геометрии. Геометрия – это пространство. Цвет, звук (в музыке) – это волна. Их гармония описывается определёнными отношениями – иррациональными величинами, самой известной из которых является золотое сечение. Золотое сечение связано с иррациональным числом √5 (корень квадратный из пяти) и равно (приблизительно, с учетом заданной точности вычисления) 1,61803398875… Золотое сечение – это гармоническая пропорция, в которой одна часть относится к другой, как всё целое к первой части. Или, другими словами, золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама бо́льшая часть относится к меньшей; или меньший отрезок так относится к большему, как больший ко всему. Формулы золотого сечения расположены выше.

Пропорция золотого сечения. Формулы

Разбиение отрезка в пропорции золотого сечения на две части приближённо можно обозначить в процентах от целого как 62% и 38%.

Я не буду подробно останавливаться сейчас на золотом сечении, поскольку оно хорошо исследовано с древнейших времён и продолжает активно изучаться. Его пропорции находят во всём совершенном, проявленном в человеке, растениях, животных и устройстве Мира. В дошедшей до нас литературе золотое сечение впервые упоминается во второй книге «Начал» Евклида, где даётся геометрическое построение на основе правильного пятиугольника. Свойства золотого сечения создали ему ореол мистического поклонения, таинственности и исключительности. Однако есть и другие гармоничные пропорции, не менее изысканные, но гораздо менее известные. Подробно гармонии начальных иррациональных чисел, неразрывно связанных с моделью Куб Метатрона и Платоновыми телами, описаны и проиллюстрированы в книге «Метатрон».

Остановлюсь только ещё на одной гармонии – древнейшей и базовой модели «Весика Пискис» (или Весика Писцис от лат. Vesica piscis – рыбий пузырь). Весика Пискис – это центральная фигура, образованная пересечением двух кругов с одинаковым радиусом, наложенных так, что центр одного лежит на окружности другого (схема 1, рис. 1). Если нарисовать прямые линии, соединяющие центры обеих окружностей и вершины фигуры, получатся два равносторонних треугольника (схема 1, рис. 3).

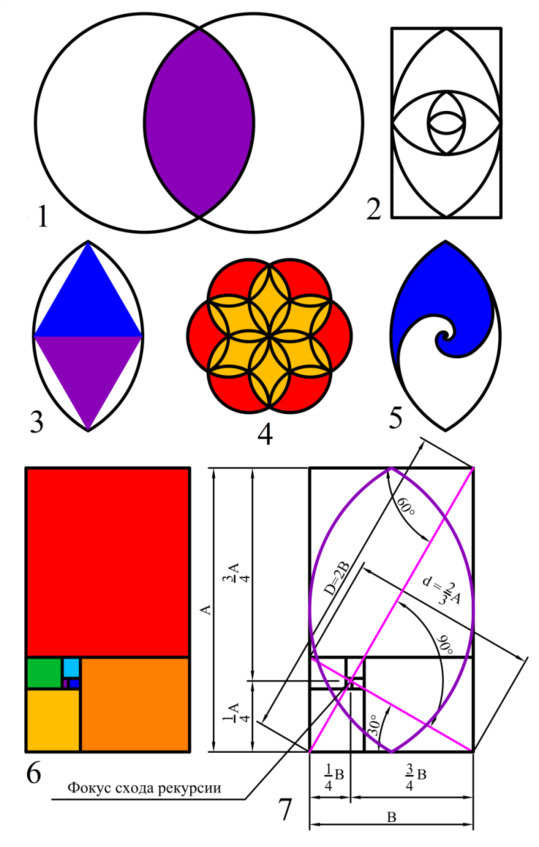
Схема 1. Весика Пискис. 1 – построение из двух окружностей; 2 – пропорциональное членение пропорцией; 3 – схема с правильными равносторонними вписанными треугольниками; 4 – базовый элемент Цветка Жизни с выделением фрагментов в форме Весика Пискис; 5 – схема со спиралью, построенной в пропорции Весика Пискис; 6 – прямоугольник с уменьшающейся рекурсией в фокус схода; 7 – основные пропорции прямоугольника Весика Пискис с рекурсией.

Рекурсия пропорций Весика Пискис построена на иррациональной величине √3 (корень квадратный из трёх). Математическое соотношение высоты (А) и ширины (В) фигуры равно √3, или (приблизительно, с учётом заданной точности вычисления) 1,7320508… При создании вписанных или взаимодействующих фигур в этой пропорции, пропорционально убывающих или увеличивающихся, каждая следующая фигура, вписанная в предыдущую, будет меньше её на √3 при убывании размеров или больше на √3 при их увеличении. Если же рассмотреть пропорции фигур через одну, то их размер будет ровно в три раза меньше или больше относительно базовой. Точка фокуса этой рекурсии имеет простое и понятное местонахождение – одна четвёртая размера стороны прямоугольника, разумеется, относительно любой стороны фигуры и прямоугольника любого размера (схема 1, рис. 7). Диагональ в прямоугольнике гармонии Весика Пискис равна удвоенной меньшей стороне прямоугольника. В модели Куб Метатрона эта рекурсия заложена в пропорции Платоновых тел Куба и Октаэдра и описана в соответствующих главах книги «Метатрон». Рекурсия модели Весика Пискис вглубь или наружу может быть продолжена бесконечно без каких-либо изменений пропорций и дефекта базовой формы. При выполнении таких многоразовых операций части остаются идентичными исходной фигуре, имея все свойства, присущие ей. Весика Пискис проявляет прогрессирующую способность прохождения к бесконечно малому и бесконечно большому со всеми свойствами, бесконечно повторяющими самих себя во всех направлениях бесконечного пространства. Это признак гармонии и гармоничных пропорций и отношений. Весика Пискис является основой построения Цветка Жизни – базовой модели сакральной геометрии (схема 1, рис. 4). Первый элемент Цветка Жизни образован вращением (размножением) внешнего круга вокруг центрального через 60 градусов, то есть шестикратным повтором; таким образом, Весика Пискис образует элементы Цветка Жизни в многочисленных проявлениях, уплотняя и насыщая его гармонией своих пропорций.

Автор Татьяна Фёдорова