29
Синусный метод

Мы всегда можем рассчитывать, что Шелдон проигнорирует суть, обратив внимание только на слова, но в этот раз это странно, поскольку то, что он трактовал неверно, было не сигналы в общении, а математика.

Тремя наиболее часто встречающимися системами единиц для измерения углов являются градусы, радианы и грады. (Один градус немного больше града и гораздо меньше радиана.) Одни легко превратить в другие: надо только умножить или разделить (см. главу 5). Труднее запомнить, какой системой вы пользуетесь. Если вы забудете упомянуть название единицы измерения после числа или случайно назовете другую, вы рискуете создать катастрофу. Когда вы делаете сноубордисту вызов «выдать 720», а он соглашается, имеет ли он в виду ту же самую единицу измерения? Если он сделает два полных оборота, это и будет 720 градусов; если же он сделает только один поворот и три четверти и приземлится на все лицо, он всегда может сказать, что подумал, будто вы имели в виду 720 градов. Что же касается 720 радианов, или 115 полных оборотов, то вряд ли можно на них рассчитывать – даже во «Всемирных экстремальных играх».

Существуют менее путаные способы описания углов. Они используют измерения без каких-либо единиц. Например, синус угла – это просто число, так же как и тангенс угла наклона (угловой коэффициент). Причина, по которой синус и тангенс не используют никаких единиц измерений, в том, что они дробные: длина одной стороны треугольника, поделенная на длину другой.

Вот в чем смысл: мы рисуем две линии, которые пересекаются под определенным углом. Затем мы рисуем третью линию, пересекающую две предыдущие и перпендикулярную одной или второй. Любая линия подойдет, лишь бы угол, который она образует с одной из этих линий, был прямым (в девяносто градусов).

Пересечение трех линий образует треугольник. Обозначьте последнюю сторону буквой А и измерьте все три стороны. Синусом нашего угла будет длина А, поделенная на длину самой длинной стороны треугольника. Угловым коэффициентом нашего угла будет длина А, поделенная на длину оставшейся стороны.

Вот еще один способ, как это можно представить: возьмите прямую лестницу и поставьте ее к стене под любым углом, лишь бы верхний конец касался стены. Теперь сделайте три измерения: как высоко от земли находится верхний конец лестницы, как далеко от стены находится нижний конец лестницы и длину самой лестницы. Эти три величины образуют три стороны треугольника с правильным углом там, где стена встречается с землей. Лестница находится под определенным углом к земле: ноль градусов, если она на ней лежит, девяносто градусов, если она плотно прижата к стене, или любое другое число в зависимости от ее наклона, если она поставлена к стене верхним концом. Этот угол нас и интересует, и мы можем определить его синус и тангенс углового наклона, используя три полученные длины.

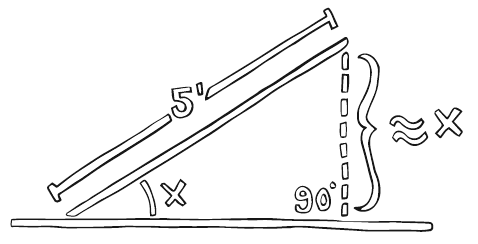
Синус нашего угла – это расстояние вверх по стене (от земли до верхнего конца лестницы), поделенное на длину лестницы. Это будет доля между нулем и единицей. Если длина лестницы четыре фута и ее верхний конец находится на расстоянии одного фута от земли, то синус равен 0,25 (¹/₄ = 0,25).

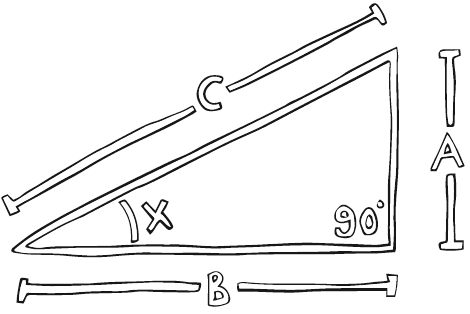
Синус угла х – это А (вертикальная величина), поделенная на С (длина лестницы). Угловой коэффициент х – это А (вертикальная величина), поделенная на В (горизонтальная величина)

Угловой коэффициент нашего угла – это расстояние вверх по стене, поделенное не на длину лестницы, а на расстояние от нижнего конца лестницы до стены. Длина лестницы не имеет значения, а угловой коэффициент часто выражается в процентах. Если нижняя часть лестницы расположена на два фута от стены, а ее верхняя – на один фут, то это 50% угловой коэффициент (¹/₂ = 50%). Если оба расстояния одинаковы, то это 100% коэффициент. Если нижняя часть находится в одном футе от стены, а верхняя в двух, то коэффициент – 200% (²/₁ = 200%).

Если лестница плотно прижата к стене, расстояние вверх по стене равно ее длине, тогда как расстояние по земле равно нулю. Синус угла (расстояние вверх по стене, поделенное на длину лестницы) равен единице, а угловой коэффициент (расстояние вверх по стене, поделенное на расстояние по земле) обращается к бесконечности. Когда лестница лежит плашмя на земле, расстояние по земле равно длине лестницы, а расстояние вверх по стене равно нулю. Синус такого угла равен нулю, а угловой коэффициент угла – 0%. Между этими положениями (когда лестница стоит под наклоном к стене) оба расстояния, вверх по стене и расстояние по земле до стены, меньше длины лестницы, но больше нуля. В этих случаях синус будет между нулем и единицей, тогда как тангенс угла наклона будет от 0% до бесконечности. (Если бы угол был направлен вниз, синус опустится до –1, угловой коэффициент обратится к отрицательной бесконечности.)

Длина лестницы нас не волнует совершенно. Если бы вы использовали лестницу подлинее, измеряемые расстояния увеличились бы соответственно. Деление этих расстояний даст вам абсолютно такой же синус и тангенс наклона угла. (Посмотрите, что произойдет на диаграмме, когда мы заменим лестницу с длиной C на лестницу с длиной F.)

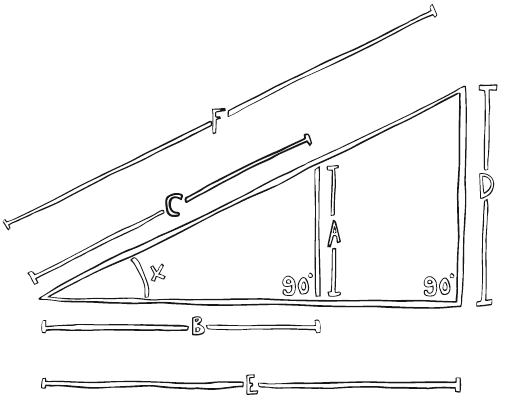
^A/_C = ^D/_F = синус угла х. ^A/_B = ^D/_E = тангенс наклона угла x.

«Кому нужны эти синусы?» – скажете вы. Ну, для начала, Шелдону и Леонарду. Они толкают коробку вверх по лестнице, а синус скажет им, на какую высоту они смогут ее поднять, протащив ее на определенное расстояние. Синус 30-градусного угла их лестницы равен (спасибо, Шелдон) ровно половине – 0,5, что означает, что для поднятия коробки на один фут в высоту им нужно будет протащить ее два фута по лестнице. Это в два раза больше, чем если бы они передвигали ее вертикально, но гораздо легче.

А кому нужны тангенсы углового наклона? Ну например, архитекторам, которые спроектировали здание, в котором живут Шелдон и Леонард: угловой коэффициент сообщает, сколько горизонтального пространства понадобится лестнице определенной высоты. Тангенс наклона угла в 30 градусов – около 58%, что означает, что лестница займет около фута на каждые семь дюймов, на которые она идет вверх. Судя по размеру окна в гостиной Шелдона и Леонарда, вертикальное расстояние от одного этажа до другого должно быть по крайней мере пятнадцать футов. Чтобы подняться на такую высоту, один пролет должен покрывать горизонтальное расстояние хотя бы в 26 футов, если не больше, не учитывая расстояния для площадок. Если бы лестница не шла вокруг лифта, она никогда бы не поместилась в здании.

Углы, синусы и тангенсы увеличиваются и уменьшаются вместе, но по-разному. Допустим, наша лестница находится под углом всего в несколько градусов от земли. После того как мы измерим все расстояния и определим синус и тангенс наклона угла, мы подвинем нижний конец лестницы немного ближе к стене – ровно настолько, чтобы лестница образовывала угол с количеством градусов в два раза от первоначального. Ее верхняя часть немного подползет вверх. Угол удвоился, расстояние на земле уменьшилось, а расстояние вверх по стене увеличилось. (Длина лестницы осталась неизменной, само собой.) Теперь, когда мы выполним деление, мы получим больший синус и тангенс, но необязательно вдвое больше.

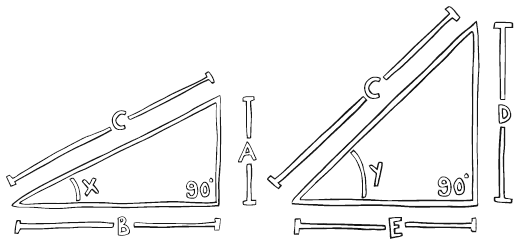
Угол y больше (в градусах), чем угол х, а расстояние D больше, чем А, тогда как E меньше B. Поэтому синус (= ^D/_C) и угловой коэффициент (= ^D/_E) y больше, чем синус (= ^A/_C) и тангенс (^A/_B) x.

На рисунке угол y в два раза больше x, но D не вдвое больше A, а E короче B. Поэтому синус y (= ^D/_C) не в два раза больше, чем синус x (= ^A/_C), тогда как тангенс угла наклона y (= ^D/_E) увеличился немного больше, чем в два раза от тангенса x (= ^A/_B).

Каждый угол между нулем и девяноста градусами обладает своим синусом и тангенсом наклона угла. Если вы знаете угол, то вы можете посмотреть (или рассчитать) синус и тангенс и наоборот. Но вам, возможно, не придется это делать.

Строители знают, как быстро рассчитать углы. Чтобы найти угловой коэффициент поверхности, нужно:

• положить один конец восьмифутовой доски (стандартная длина) на землю;

• поднять или опустить второй конец, пока доска не выровняется;

• измерить высоту этого конца над землей.

Это расстояние (в дюймах) приблизительно равно угловому коэффициенту (в процентах). (Причина, по которой работает этот трюк, в том, что восемь футов всего на несколько процентов не дотягивает до 100 дюймов. Вы можете увеличить точность, добавив дюйм на каждые полученные два фута.)

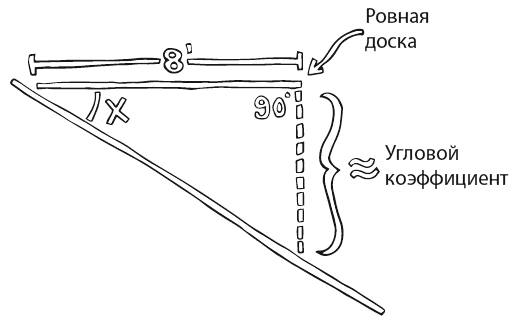
Измерение расстояния вниз по прямой: дюймы ≈ угловому коэффициенту (в процентах)

Чтобы найти угол наклонной доски, нужно:

• найти точку в пяти футах от нижнего конца доски и измерить ее высоту;

• если высота больше одного ярда (36 дюймов), добавьте два дюйма.

Это измерение (в дюймах) дает число с погрешностью в один градус в углах, вплоть до 45 градусов. Для углов больше 45 градусов измерьте стороны и вычтите результат из 90. (Причина, по которой работает этот трюк, гораздо сложнее. Не заморачивайтесь .)

Измерение вниз по прямой: дюймы ≈ угол (в градусах)

Давайте на минуточку посмотрим на циферблат часов. (На самом деле, это займет больше минуточки – и нет смысла скрывать этот факт, раз мы смотрим на часы.) На нем обычно бывают двенадцать отметок, указывающие часы. За один час часовая стрелка двигается от одной отметки до другой (30 градусов), тогда как минутная стрелка проходит полный круг в 360 градусов, проходя через все двенадцать.

Угол между двумя соседними отметками, в 30 градусов, – добрый друг математиков и инженеров, но часы здесь ни при чем. Увидеть угол в 30 градусов – это все равно что заметить знакомое дерево посреди тропического леса . Причина в том, что у большинства углов отвратительные синусы. Возьмите 60 градусов, например: такое хорошее круглое число, а вот его синус – неприятное сочетание цифр (немного больше 0,866025). Угол в 45 градусов не лучше: его синус чуть больше 0,707106 . Но 30 градусов очень особенны. Их синус равен ровно одной второй – чистая дружелюбная доля. По какому бы диагональному расстоянию вы ни путешествовали, поднимаясь по 30-градусной лестнице, вы поднимаетесь ровно на половину этой высоты.

Вам может показаться, что цифра должна быть меньше, поскольку 30 градусов – это какой-то тощий угол. Если вы положите коробку длиной в шесть футов на эту лестницу, окажется ли ее верхний конец в трех футах (= 6 футов × ¹/₂) – ровно в трех футах – над ее нижним концом? Окажется. Синус 30 градусов на самом деле равен ¹/₂.

Так что Леонард говорит, что количество прилагаемых усилий для поднятия коробки в горизонтальном положении уменьшится примерно вдвое по сравнению с ее вертикальным перемещением, потому что угол примерно равен 30 градусам. Шелдон, пропустив второе «примерно», обижается на тот факт, что синус ровно 30 градусов вдруг оказался не ровно 1/2, и спешит со своими занудными исправлениями.

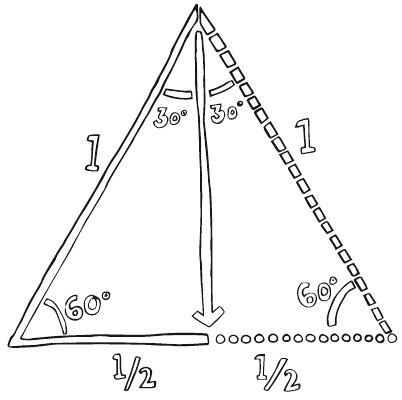
Доказательство, что синус 30° = ¹/₂. Все три угла равностороннего треугольника равны 60 градусам, а точечная линия половины основания равна половине стороны, обозначенной пунктирной линией

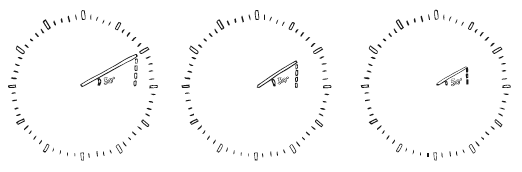
В два часа часовая стрелка образует 30-градусный угол с воображаемой горизонтальной линией. На этой диаграмме вертикальная пунктирная линия соединяет эту линию с часовой стрелкой. Поскольку синус 30° = ¹/₂, пунктирная линия равна половине длины часовой стрелки, хоть она и кажется гораздо короче. Это остается верным независимо от длины стрелки

Особенность слова «синус» в том, что оно не очень удачно выбрано (по крайней мере для английского языка, где оно звучит абсолютно одинаково с другим математическим термином: sine «синус» и sign «знак»). Оно не только смущает англоязычных математиков и ученых (вы сами до сих пор качаете головой от всех градусов, минут и секунд), слово «синус» еще необычно и по другой причине, исходящей из 900-летней ошибки в переводе.

С добавлением окружности легко увидеть связь синуса с (половиной) тетивы лука. Не хватает только маленького лучника

В XII веке ученый человек по имени Герард Кремонский делал перевод на латынь арабского перевода индийской книги по геометрии. Ему попалось слово «jiba», транслитерация слова из санскрита, означавшего «линия, разрезающая окружность» или «тетива». Вполне оправданно Герард принял слово «jiba» за совершенно другое (jaib), которое писалось абсолютно идентично в арабском, но означало (помимо всего прочего) «складка в одежде». В латинском «складка в одежде» – это «sinus», поэтому он и использовал это слово. Когда перевод Герарда был использован для английского варианта, он превратился в «sine», а в некоторых остался как «синус».

Вообще-то слово «синус» в латинском может означать не только «складка в одежде», но и «залив», «карман», «полость внутри черепных костей» или «кусок земли внутри изгиба извилистой реки». Вы видите связь между этими понятиями: они все обозначают выпуклые области. Но ни одно из них не похоже на линию, разрезающую окружность. Ай-яй-яй, Герард.

График, представляющий синус любого угла, называется синусоидной кривой или синусоидой. Эта форма ассоциируется со многими физическими процессами, например импульсными волнами, описанными в главе 25. Интересно, что синусоида извивается, как изгибы извилистой реки. По странному стечению обстоятельства график имитирует случайное ошибочное название.

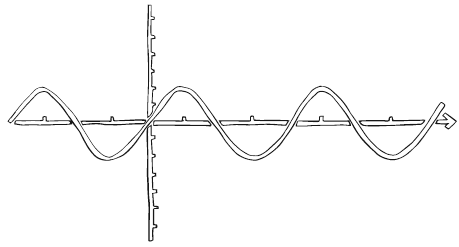
Герард так и не дожил, чтобы увидеть, как выглядит синусоидная кривая; первая из них была изображена гораздо позднее того момента, как он навсегда скрылся за изгибом реки. Но как же здорово ее маленькие карманы и заливы реабилитируют его случайное лингвистическое отклонение!

Откуда мы знаем, что ступеньки в доме поднимаются по углом в 30 градусов? Вы могли бы измерить угол перил, которые проходят за лифтом, но это не обязательно; наклон в 30 градусов типичен для большинства лестниц в США и Канаде. Лестницы с меньшим градусом заняли бы слишком много горизонтального пространства, а по более крутым ступенькам гораздо труднее взбираться. Попробуйте сами: найдите линейку и лестницу и измерьте сами. Диагональ от одной ступени до другой будет примерно вдвое больше подъема.

Лестница – это пример трудосберегающей конструкции, названной наклонной плоскостью. Протягивание коробки с предметом мебели затребует меньше силы, чем ее вертикальное перемещение, из-за прохождения более длинной дистанции.

Поскольку работа определена как сила, помноженная на расстояние (чем тяжелее что-то или чем выше вы это поднимаете, тем больше требуется работы), использование простого механизма не уменьшает общее количество работы, как утверждает Шелдон в двух разных контекстах в одном только первом сезоне.

• В процессе затаскивания наверх 200-фунтовой копии машины времени Г. Дж. Уэллса: «Количество работы не уменьшается от скорости ее выполнения. Это же основы физики» .

• Объясняя Пенни, почему световой год – это мера расстояния, а не времени: «С килограммометром та же проблема, все думают, что это единица веса, а не работы» .

Но простые механизмы снижают количество необходимой силы, что важно для парочки физиков, у которых нет «ни тележки, ни специальных ремней, ни какой бы то ни было мышечной массы». Разве было бы не легче отвезти коробку наверх? Может быть, на скутере Говарда? Скорее всего, нет. Удивительно, но хоть наклон в 58% 30-градусной лестницы вполне удобен для пешеходов (в отсутствие работающего лифта), он крутоват для безопасного передвижения транспортных средств. За парой исключений, самые крутые улицы в мире имеют угловой коэффициент гораздо ниже 40% – что соответствует углу в 20 градусов. Поезда натыкаются на трудности уже на однопроцентных холмах (угол в полградуса).

А нужна ли вся эта тригонометрия только для того, чтобы поднять шестифутовую коробку вверх по лестнице? Вам не надо знать все о синусах и тангенсах, чтобы понять, что тянуть ее по покрытым ковром ступенькам легче, чем нести. Единственная разница в том, что тогда вы не сможете рассчитать, сколько именно усилий вы экономите. И вы не будете знать, что будет означать наклон лестницы, когда верхняя часть коробки окажется на три фута выше (= 6 футов × синус 30°), чем нижняя часть. Хотя, когда нужно выполнять работу, никто не жалует всезнаек.

У древних египтян не было синусов, картонных коробок или покрытых ковром лестниц. Но каким-то образом они умудрялись поднимать огромные каменные глыбы и складывать их в памятники, обелиски и пирамиды. Возможно, они использовали систему рамп, чтобы передвигать части пирамиды в нужное положение. Чем более пологий угол, тем длиннее дистанция, на которую нужно протащить предмет, чтобы попасть на нужную высоту, но (благодаря синусу) тем легче это сделать. А метод рамп, несомненно, существовал сорок веков назад.

Но обелиски – совсем другое дело. Как можно поднять сплошной кусок каменной колонны в вертикальное положение с земли?

Фанат истории Морин Клеммонс задумалась, не использовалась ли ветряная сила для этой задачи. Она обсудила эту возможность с калтеховским профессором в области аэронавтики Мори Гарибом, который и протестировал ее. Он построил пятнадцатифутовый цементный обелиск, уложил его на землю и прицепил к его верхушке воздушного змея.

В умеренно ветреный день воздушный змей поднял этого трехтонного монстра в вертикальное положение за полминуты. Если вам кажется сомнительным, что единственный воздушный змей мог поднять такой вес, вспомните, что змею не нужно было поднимать весь обелиск; ему нужно было поднять только один его конец. Второй конец оставался на земле, приняв бо́льшую часть веса на себя. А синус уже доделал все до конца.

Леонард выбрал немного не те слова, когда сказал, что сила «уменьшается пропорционально синусу угла наклона». Он имел в виду «уменьшается пропорционально единице минус синус угла наклона». Чтобы понять, о чем речь, представьте другой угол: например, в 50 градусов. Он сделает ступеньки очень крутыми, и проталкивание коробки вверх по ним будет настолько же трудным, как и перемещение ее вертикально. Синус 50 градусов равен примерно ³/₄, но это не значит, что потребующаяся сила уменьшится на ³/₄; она уменьшится только на ¹/₄.

Но он нервничает, торопится, и он не архитектор, так что давайте его простим. К счастью для него, Шелдон тоже не заметил его ошибки.