Приложение 1
Математика относительности
Это приложение предназначено для тех, кто хотел бы видеть и понимать алгебру и конкретные расчеты, стоящие за теми результатами, которые мы обсуждали в тексте.
В специальной теории относительности каждому событию соответствуют положение в пространстве x и время t. Чтобы не усложнять ситуацию, давайте считать остальные пространственные координаты – y и z – равными нулю. Обозначим координаты и время событий во второй системе координат, движущейся относительно первой со скоростью v, заглавными буквами X и T. Эйнштейн определил, что верные отношения x, t, X и T задаются преобразованиями Лоренца:
X = γ(x − vt)T = γ(t − xv/c²),
где c – скорость света, а коэффициент замедления времени гамма представлен греческой буквой γ и задается как γ = 1/√(1 − β²), где греческая буква β (бета) представляет отношение скорости объекта к скорости света (β = v/c). По умолчанию в этих уравнениях считается, что особое событие (0, 0) в обеих системах отсчета имеет одинаковые координаты.
Хендрик Лоренц был первым, кто записал эти уравнения и показал, что Максвелловы уравнения электромагнетизма им удовлетворяют. Но только Эйнштейн сумел понять, что они представляют реальные изменения в поведении пространства и времени, а затем и применить их для вывода новых уравнений физики. Уравнения Максвелла при этом изменять не потребовалось, а вот уравнения Ньютона пришлось менять, и Эйнштейн заключил, помимо всего прочего, что масса движущихся объектов увеличивается (я говорю здесь о релятивистской массе, рассчитываемой как γm) и что E = mc².
У преобразования Лоренца есть замечательное свойство: при решении его уравнений относительно x и t получаются уравнения одинакового вида, за исключением знака при скорости. (При решении используется довольно хитрая алгебра, и придется использовать приведенное выше определение γ, но попытайтесь.) Вот результат:
x = γ(X + vT);
t = γ(T + Xv/c²).
В сравнении с предыдущими уравнениями изменение знака (с − на +) – это именно то, чего и следовало ожидать, поскольку по отношению ко второй СО первая система движется со скоростью −v. Тем не менее кажется поразительным, что уравнение имеет тот же вид. Я бы ни за что не догадался, что так получится. Этот факт – часть чуда теории относительности, согласно которой все инерциальные системы отсчета равно годятся для записи уравнений физики.
Растяжение времени
А теперь рассмотрим растяжение времени. Мы будем пользоваться той же терминологией, что и в примере с парадоксом близнецов, о котором шла речь в . Напомню, что Мэри там отправляется к далекой звезде, тогда как Джон остается дома. Назовем первую систему отсчета системой Джона, а вторую, которая движется относительно первой со скоростью v, системой Мэри. (Это их собственные системы отсчета.) Рассмотрим два события: 1-й и 2-й дни рождения Мэри. Обозначим их время и место в системе Джона как x1, t1 и x2, t2. Место и время этих же событий в системе Мэри обозначим как X1, T1 и X2, T2.
А теперь подставим эти величины в уравнения Лоренца. Воспользуемся второй системой:
t2 = γ(T2 + X2v/c²);t1 = γ(T1 + X1v/c²).
Вычтя второе уравнение из первого, получим:
t2 − t1 = γ[T2 − T1 + (X2 − X1)v/c²].
Возраст Мэри, измеренный в системе отсчета Мэри, составит T2 − T1. В этой системе отсчета Мэри не движется, поэтому X2 = X1, то есть X2 − X1 = 0. Поэтому уравнение упрощается до вида:
t2 − t1 = γ(T2 − T1).
Можно записать это уравнение в еще более простом виде, если использовать обозначение Δt = t2 − t1 и ΔT = T2 − T1. (Δ – заглавная греческая буква дельта, которая часто используется для обозначения разностей. Вслух Δt читается как «дельта тэ».) С использованием этого обозначения уравнение принимает вид:
Δt = γΔT.
Это и есть растяжение времени. Промежуток времени между двумя событиями в системе отсчета Джона больше, чем промежуток времени между теми же событиями в системе отсчета Мэри, в γ раз. В примере с парадоксом близнецов, описанном в , коэффициент γ равнялся 2, так что Мэри, чтобы постареть на 8 лет, потребуется (в системе отсчета Джона) 16 лет.
Линейное сжатие
А теперь посмотрим на линейное сжатие, или изменение длины. При измерении расстояния между объектами в любой системе отсчета мы отмечаем положение (координаты) объектов в один и тот же момент времени и вычитаем одно из другого. Расстояние между двумя одновременными событиями (t2 = t1) в собственной системе отсчета Джона составляет x2 − x1. Применим первую систему уравнений Лоренца к этим двум событиям:
X2 = γ(x2 − vt2);X1 = γ(x1 − vt1).
Вычтя второе уравнение из первого, получим:
X2 − X1 = γ[x2 − x1 − v(t2 − t1)].
Поскольку для этого примера два события одновременны в системе отсчета Джона, t2 = t1, множитель (t2 − t1) = 0. При подстановке этого значения уравнение упрощается до вида:
X2 − X1 = γ(x2 − x1).
Расстояние между двумя событиями в собственной системе отсчета Джона составляет x2 − x1; обозначим эту величину Δx. Длина того же объекта в собственной системе отсчета Мэри (в которой объект покоится) составляет X2 − X1; обозначим это ΔX. Получаем уравнение:
Δx = ΔX/γ.
Это и есть уравнение линейного сжатия. Если длина объекта в собственной системе отсчета составляет ΔX, то при измерении в другой системе отсчета эта длина изменится в 1/γ раз. (Обратите внимание: γ всегда больше 1, поэтому длина, то есть линейный размер объекта уменьшится.)
Одновременность
Временная разница между двумя событиями равна t2 − t1 = Δt. В другой системе отсчета эти события происходят в моменты времени T2 и T1, а временной интервал в этой системе отсчета составит T2 − T1 = ΔT. Мы также обозначим разницу координат двух событий (то есть расстояние между ними) в системе Джона Δx, а расстояние между ними в системе Мэри ΔX. Воспользовавшись первым преобразованием Лоренца для времени, получим:
T2 = γ(t2 − x2v/c²);T1 = γ(t1 − x1v/c²).
Вычитаем одно уравнение из другого и подставляем Δt, ΔT и Δx:
ΔT = γ(Δt − Δxv/c²).
В особом случае, когда в системе Джона оба события происходят одновременно (то есть когда Δt = 0), уравнение упрощается до вида:
ΔT = −γΔxv/c².
Замечательность результата в том, что ΔT – необязательно нуль. Это значит, что в собственной СО Мэри эти события необязательно одновременны, хотя в собственной СО Джона они происходят в один и тот же момент времени. Если я обозначу расстояние между двумя событиями Δx = −D (знак здесь может быть как плюс, так и минус, в зависимости от расположения x1 и x2), уравнение примет вид:
ΔT = γDv/c².
Если ни v, ни D не равны нулю, ΔT тоже не равно нулю, и это означает, что два события не одновременны в системе Мэри. Это «временной скачок», который возникает у отдаленного события при переключении с одной системы отсчета на другую. Скачка не возникает, если D = 0, то есть если два события происходят в одной точке (скажем, если Джон и Мэри вновь соединятся). ΔT может быть положительным или отрицательным, в зависимости от знаков D и v.
Скорости объектов и скорость света
Здесь я покажу, почему скорость света одинакова во всех системах отсчета.
Если некоторый объект движется, мы можем обозначить как x1 его координату в момент времени t1 и как x2 – его координату в момент t2. Представьте, что на самом деле это два события. Скорость нашего объекта такова: v = (x2 − x1)/(t2 − t1) = Δx/Δt. В другой системе отсчета: V = (X2 − X1)/(T2 − T1) = ΔX/ΔT. Мы можем воспользоваться преобразованием Лоренца, чтобы сравнить эти две величины. Обозначим буквой u относительную скорость двух СО, чтобы можно было использовать v и V для обозначения скорости объекта в каждой из двух систем. Запишем преобразование для двух событий и вычтем одно из другого:
ΔX = X2 − X1 = γ[(x2 − x1) − u(t2 − t1)] = γ[Δx − uΔt];ΔT = T2 − T1 = γ[(t2 − t1) − u(x2 − x1)/c²] = γ[Δt − uΔx/c²].
А теперь разделим одно уравнение на другое, чтобы исключить γ:

Это уравнение для преобразования скорости, позволяющее выразить скорость V во второй системе отсчета через v – скорость в первой системе отсчета.
Пусть v = c, то есть объект (к примеру, фотон) движется со скоростью света в первой СО. Во второй системе отсчета его скорость равна:
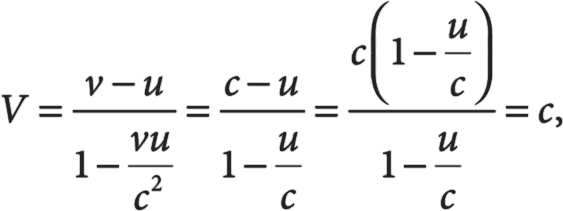
вне зависимости от u, относительной взаимной скорости двух систем отсчета. Если v = c, то V = c. Объекты, движущиеся со скоростью света в какой-то одной системе отсчета, движутся с той же скоростью и во всех остальных системах. Попробуйте подставить в уравнение v = −c и посмотрите, что получится. Удивлены?
Аналогичный вывод показывает, что c не меняется даже при произвольном направлении света.
Этот результат объясняет неудачу опыта Майкельсона−Морли в 1887 году, когда исследователи хотели обнаружить разницу скорости света в двух направлениях, первое из которых параллельно движению Земли, а второе – перпендикулярно этому движению.
Время-перевертыш
Очень интересные вещи происходят, если два разделенных события близки по времени. Воспользуемся еще одним уравнением (взятым из приведенных выше рассуждений об одновременности):
ΔT = γ(Δt − vΔx/c²) = γΔt[1 − (Δx/Δt)(v/c²)].
Определим ∆x/∆t = VE. Это псевдоскорость, которая «соединяет» два события. Записанное нами вовсе не означает, что чему-то действительно придется двигаться от одного события к другому; это просто скорость, с которой нужно было бы двигаться, чтобы присутствовать при обоих событиях. Может ли VE быть больше c? Да, конечно. Любые два разделенных события, которые происходят одновременно, имеют бесконечную VE. Это не физическая скорость. Используя эту новую величину, мы можем записать:
ΔT = γΔt(1 − VEv/c²).
Будем считать для примера, что разность ∆t положительна. Уравнение показывает, что ∆T, в принципе, может быть и отрицательной. Для этого нужно всего лишь, чтобы отрицательное слагаемое в скобках было по модулю больше 1. Это означает, что в новой системе порядок событий может смениться на обратный. Такой результат может повлечь за собой самые разные следствия для причинной зависимости.
Чтобы VEv/c² было больше единицы, VE/c должно быть больше, чем c/v. Не забывайте, v – это скорость, связывающая две системы отсчета; она в любых обстоятельствах должна быть меньше c. Это означает, что c/v всегда будет больше единицы. Это уравнение говорит, что если VE/c больше, чем c/v (что тоже делает его больше единицы), то порядок событий в двух системах отсчета меняется на обратный. Еще раз обратите внимание, что величина VE ничем не ограничена, поскольку это всего лишь псевдоскорость, призванная «соединить» два события, и что для двух сильно разнесенных в пространстве событий, но происходящих одновременно, величина VE будет бесконечна.
Математика парадокса шеста и сарая
Обратимся вновь к . В системе отсчета, связанной с сараем, шест входит концом в дверь и продолжает двигаться, пока не упрется в заднюю стену. Определим t1 = 0 как момент, когда передний конец шеста доходит до задней стены, и выберем систему координат так, что в этой точке x1 = 0. Из-за лоренцева сжатия в системе отсчета, связанной с сараем, задний конец шеста поравняется с дверью в этот же момент, при t2 = 0, в точке x2 = −6 м.
Теперь рассчитаем, что происходит в системе отсчета, связанной с шестом. Передний конец шеста упрется в заднюю стену сарая в момент T1 с учетом уравнения преобразования Лоренца:
T1 = γ(t1 − x1v/c²) = 2(0 − 0v/c²) = 0.
Задний конец шеста поравняется с дверью в момент:
T2 = γ(t2 − x2v/c²) = 2(0 + 6v/c²).
Вычислив v/c из γ = 2, получаем β = v/c = 0,866. Таким образом:
T2 = 2(0 + 5,196/c) = 10,392/c.
Воспользовавшись значением скорости света c = 3·108 метров в секунду (м/с), получим, что шест целиком войдет в сарай за T2 = 34,64/109 с = 34,64 × 10−9 с. Так что в момент, когда передний конец шеста упрется в стену, задний его конец еще не дойдет до двери. Она поравняется с ней через 34,64 наносекунды (миллиардной доли секунды).
Вычислим в системе отсчета, связанной с шестом, где будет находиться его задний конец, когда передний упрется в стену. Воспользуемся уравнением:
x2 = γ(X2 + vT2).
Решив его относительно X2 и подставив v = 0,866c, x2 = −6 метров и T2 = 10,392/c, получаем:
X2 = x2/γ − vT2 = −6/2 − 9 = −12 (метров).
Этот ответ вполне соответствует нашим ожиданиям. В системе шеста, когда передняя его часть упирается в стену, задняя находится от нее на расстоянии −12 метров. Эта точка отстоит на 12 метров от задней стены сарая, что соответствует данным, что шест в этой системе отсчета имеет длину 12 метров.
Разрешение парадокса кроется в том, что два конца шеста одновременно находятся внутри сарая в системе отсчета, связанной с сараем, но в системе, связанной с шестом, они, хотя и попадают оба внутрь сарая, но делают это не одновременно: задний конец шеста проходит в дверь чуть позже, чем передний упирается в стену. Когда шест оказывается внутри, если его движение внезапно прекращается (оба конца шеста в системе сарая останавливаются одновременно), он потеряет свое линейное сжатие и внезапно удлинится до полной 12-метровой длины, проломив при этом какую-то из стен сарая или обе.
Математика парадокса близнецов
Поскольку для Мэри замедление времени составляет γ = 2, мы можем рассчитать, что отношение ее скорости к скорости света равно β = 0,866. В этом примере парадокса близнецов есть несколько важных систем отсчета: СО Джона (мы будем называть ее системой Земли), удаляющаяся система отсчета Мэри (собственная СО Мэри на пути туда, движущаяся со скоростью v = 0,866c) и приближающаяся система отсчета Мэри (ее собственная СО на обратном пути, движущаяся со скоростью v = −0,866c). Наконец, собственная система отсчета Мэри представляет собой комбинацию двух перечисленных, поскольку она какое-то время движется с ускорением и переходит из одной лоренцевой системы в другую.
В системе Земли мы можем вычислить расстояние до интересующей нас звезды из того факта, что Мэри летит к ней со скоростью, равной 0,866 скорости света, и весь путь занимает 8 лет; это расстояние равно 0,866 × c × 8 = 6,92c, или 6,92 световых года. В собственных системах отсчета Мэри при удалении от Земли и возвращении к ней расстояние составляет 6,92c, деленное на коэффициент лоренцева сжатия γ, то есть 3,46c. В системе Мэри время, которое занимает у нее путь к звезде, равно расстоянию 3,46c, деленному на скорость 0,866c, и равно 4 годам. Так что и в системе Земли, и в удаляющейся системе Мэри, когда она долетит до звезды, будет 4 года. Точно так же на обратном пути она подрастет еще на четыре года, и по возвращении ей будет 8 лет.
Джон в системе Земли покоится. В этой системе путешествие Мэри занимает 8 лет в одну сторону. Когда Мэри вернется, Джон будет старше нее, ему исполнится 16 лет.
А теперь рассмотрим те же события в системе отсчета, связанной с Мэри. Эта система движется с ускорением, поэтому мы будем проводить вычисления в три этапа. Сначала воспользуемся ее удаляющейся системой, которая движется со скоростью +v относительно систем Земли. Затем она на какое-то время остановится у далекой планеты; ее собственная система станет идентична системе Джона; наконец, она отправится в обратный путь, разгонится, и ее собственная система будет двигаться со скоростью −v относительно системы Земли.
На первом этапе, от Земли до звезды, Мэри в своей собственной системе покоится. Джон движется со скоростью −v и взрослеет со скоростью 1/γ лет. Мэри летит до звезды 4 года (конечно, в этой системе именно звезда движется к ней; сама она покоится). За это время Джон взрослеет всего на 4/γ = 2 года.
Затем Мэри останавливается у звезды (вероятно, на какой-то близлежащей планете, не на самой звезде). Теперь ее собственная система отсчета идентична системе Земли, так что, хотя ей 4 года, Джону (в этой системе) одновременно уже 8 лет. Это первый временной скачок. Дело не в том, что Джон мгновенно взрослеет; дело в том, что Мэри сменила одну лоренцеву систему отсчета на другую, и в новой ее собственной системе события, которые были одновременными в старой, больше не одновременны. Мэри знает, что в удаляющейся системе отсчета (в которой она больше не покоится), Джон по-прежнему младше нее. Но в системе планеты, идентичной земной системе, Джон старше. И Джон, и Мэри согласились бы с этими рассуждениями.
Обратите внимание: «скачок» в одновременном возрасте Джона составил 6 лет (с 2 до 8). Это соответствует уравнению временного прыжка, приведенному выше:
Δt = γ(ΔT − ΔXv/c²).
Здесь Δt – скачок возраста Джона. (Его возраст на Земле идет в соответствии с временем в земной системе отсчета.)
Далее Мэри второй раз меняет собственную систему отсчета: ускоряется для движения обратно к Земле. Подставляем ΔX = −3,46c (расстояние в возвращающейся системе), ΔT = 0 (события одновременны), γ = 2 и v/c = −0,866, получаем:
Δt = 2(0 + 3,46 × 0,866) = 6 (лет).
Это второй скачок возраста Джона, от значения в системе отсчета у звезды к его возрасту в возвращающейся системе; то и другое совпадает по времени с четвертым днем рождения Мэри. Одновременный возраст Джона в ускоряющейся собственной системе отсчета Мэри сменяется с 8 на 14. За время обратного полета Мэри Джон взрослеет еще на 2 года – и когда Мэри наконец возвращается, ему 16 лет.
Таким образом, при вычислении как в системе Джона (не испытывающей ускорений), так и в системе Мэри (испытывающей ускорения), получаем, что когда они вновь встретятся, Джону будет 16 лет, а Мэри лишь 8.
Вообще, не стоит вычислять что бы то ни было в ускоряющихся системах отсчета, если этого можно избежать. Скачки одновременности настолько контринтуитивны, что с ними трудно разбираться. Просто держитесь за любую неускоряющуюся систему отсчета – и можете быть уверены, что в любой другой системе, пойдя в вычислениях по сложному пути, вы получили бы ровно те же результаты.
Математика тахионного убийства
Назовем событием 1 выстрел из тахионного ружья, а событием 2 – смерть жертвы. Δt = t2 − t1 = +10 наносекунд, и Δx = x2 − x1 = 12 метров. Это означает, что тахион движется со скоростью 12/10 = 1,2 метра в наносекунду, то есть примерно 4c. Знак плюс означает, что жертва умирает после того, как я стреляю, поскольку значение времени смерти больше, чем значение времени выстрела.
А теперь рассмотрим эти два события в системе отсчета, движущейся со скоростью v = ½c. Тогда β = 0,5; γ = 1/√(1 − β²) = 1,55. Используем уравнение скачка времени:
ΔT = γ(Δt − Δxv/c²) = γΔt[1 − (Δx/Δt)(v/c²)].
Подставляем γ = 1,55; Δt = 10 наносекунд; v/c = 0,5 и Δx/Δt = 4с и сокращаем c, получаем:
ΔT = (1,55)(10 наносекунд)[1 − (0,5)(4)] = −15,5 наносекунды.
То, что интервал времени получился отрицательным, означает, что порядок событий изменился на обратный. Жертва застрелена в момент времени T2, но поскольку T2 − T1 меньше нуля, число T1 больше. Следовательно, T1, момент выстрела, происходит в большее – то есть более позднее – время.
Обратите внимание также, что если Δx/Δt = VE меньше, чем скорость света c, – то есть если пуля движется с досветовой скоростью, – такая смена порядка событий невозможна. Чтобы события поменялись местами, VE/c должно быть больше, чем c/v, а c/v всегда больше 1. Так что для любых двух событий, которые можно связать с помощью сигнала, движущегося со скоростью меньше скорости света, порядок, в котором они происходят, будет одинаковым для всех допустимых систем отсчета – то есть для всех систем, для которых v меньше c. Мы называем такие события времениподобными. Пространственноподобными называют события, разделенные таким большим расстоянием, что для их соединения скорости света недостаточно.
Математика гравитационного эффекта времени
Эйнштейн постулировал, что течение времени в гравитационном поле можно рассчитать исходя из предположения, что оно эквивалентно течению времени в ускоряющейся системе отсчета. Этим мы сейчас и займемся.
Предположим, у нас имеется ракета высотой h, которая находится в такой области пространства, где отсутствует гравитация. Ракета движется носом вперед с ускорением, соответствующим ускорению свободного падения в поле тяготения Земли, g = 32 фута в секунду в квадрате (9,8 м/с2). Будем считать, что верх и низ ракеты ускоряются одновременно в системе отсчета, связанной с первоначальной позицией ракеты. Через время Δt система отсчета, связанная с ракетой, движется со скоростью v = gΔt относительно первой СО (при условии, что начальная скорость ракеты равна нулю).
Воспользуемся уравнением из примера про тахионное убийство, чтобы вычислить соответствующий интервал времени в верхе ракеты:
ΔT = γ(Δt − Δxv/c²).
Подставив Δx = h и v = gΔt и считая приближенно (для нерелятивистских скоростей), что γ = 1 (β ≈ 0), получим:
ΔT = Δt − hgΔt/c².
Разделим на Δt:
ΔT/Δt = 1 − gh/c².
Отсюда видно, что на высоте h интервал времени для верха, ΔT, меньше, чем интервал времени в нижней части, Δt. Часы в верхней части ракеты идут быстрее. В более общем случае это уравнение часто записывается как:
ΔT/Δt = 1 − ø/c²,
где ø – разность гравитационных потенциалов. К примеру, потенциал на поверхности Земли, в сравнении с бесконечностью, будет: ø = GM/R, где M – масса Земли, G – гравитационная постоянная, а R – радиус Земли.
Во многих учебниках эта формула выводится совершенно иначе, из красного смещения света, направленного с верхушки некоего ящика к его основанию. Я предпочитаю тот подход, который только что изложил, потому что в нем явно используется принцип эквивалентности, положенный в основу общей теории относительности Эйнштейна; в этом подходе видно, что эффект возникает благодаря слагаемому xv/c² в уравнениях Лоренца – тому самому слагаемому, которое приводит и к нарушению одновременности.
Назад: Приложения
Дальше: Приложение 2 Время и энергия[279]

