Книга: Решение проблем по методикам спецслужб. 14 мощных инструментов
Назад: Глава 12 Адвокат дьявола
Дальше: Глава 14 Дерево анализа полезности
Глава 13
Дерево вероятностей
Вероятность – одна из более сложных для понимания и применения концепций. Мортон Хант объясняет причины этого в книге The Universe Within:
По большей части концепции и шаблоны, которые большинству людей сложно и осознать, и применять, – «неинтуитивные», то есть их нельзя вывести из повседневного опыта, в силу чего они и не представляют собой часть привычного набора инструментов, которыми пользуется наш разум. Одна из таких концепций – вероятность. Большинству удается легко найти ответы лишь на самые простые задачи, связанные с вероятностью.
Джереми Кэмпбелл в книге The Improbable Machine высказывает схожую мысль:
Кажется, людям не удается понять и освоить принципы вероятности, какие бы усилия они ни прикладывали… просто на основе постоянного наблюдения вероятностных событий в жизни… [Одно из возможных объяснений] может быть связано с тем, что правила… определения вероятности не вполне очевидны с точки зрения здравого смысла. А «здравый смысл» во многих случаях – это законы, по которым работает человеческая память и по которым сознание обрабатывает информацию.
Не больше оптимизма мы наблюдаем и в книге Нойштадта и Мэя Thinking in Time:
Судя по опыту работы с нашими студентами, мы приходим к выводу, что миллионы американцев либо не знакомы с численным выражением вероятности, либо не умеют формулировать субъективное суждение [в терминах вероятности].
Причины, по которым мы, люди, с таким трудом оцениваем вероятность, связаны с тем, что наш мозг (то есть разум) не оснащен «блоком оценки вероятностей». Мы можем интуитивно и вполне достоверно определить высоту объекта, скажем, дерева или лестницы. Можем на глаз оценить расстояния, скажем, длину комнаты. Эти оценки мы делаем исходя из визуального восприятия объектов и в таких вопросах чувствуем себя вполне уверенно. Но, когда дело доходит до не связанного с визуальными образами процесса оценки вероятностей, мы совершенно теряемся. Человеческий разум просто не приспособлен для того, чтобы размышлять в терминах математической вероятности. Нам важно учитывать эту особенность и не слишком доверять собственным оценкам в этой области.
К примеру, люди склонны считать, что, так как событие имело место в прошлом, вероятность его наступления была крайне велика. Если нам сообщают, что вероятность дождя составляет лишь 5 %, а мы отправляемся на пикник, попадаем-таки под дождь и вымокаем до нитки, мы тут же заключаем, что прогноз был неверным. Разумеется, вероятность дождя была выше, чем 5 %, – скорее уж, все 100 %! Мы же промокли! Но что на самом деле означала прогнозируемая 5 %-ная вероятность дождя, о которой нам сообщили? Что специалисты гидрометцентра собрали необходимую информацию и определили, что в 5 % случаев, когда погодные условия складывались так же, как сегодня, шел дождь. Это можно выразить и иначе: если одни и те же погодные условия, точно такие, как в этот день, повторятся много-много раз, то в 5 % случаев пойдет дождь. То есть прогноз не был ошибочным – это наша интуиция нас подвела.
Понимать суть вероятностных оценок и уметь с ними работать крайне важно – ведь именно эти оценки, в явной и неявной форме, позволяют нам анализировать ситуации и проблемы. Вероятности скрыты в данных, которые мы анализируем; на вероятности мы опираемся в ходе анализа. Если мы не понимаем влияния вероятностей на рассматриваемую проблему и не умеем их адекватно понимать и оценивать, это может полностью разрушить весь наш анализ, а выводы и рекомендации сделать бессмысленными.
Как я уже писал, самыми сложными оказываются нестандартные проблемы и задачи, где в силу недостатка информации анализ основывается исключительно на наших собственных оценочных суждениях. В работе с проблемами неопределенного характера никакой определенности быть не может. Вообще никакой определенности! Как только мы в ходе анализа переходим от строгих фактов к оценочным суждениям, всякая определенность заканчивается – и начинаются вероятностные оценки. «Когда нам не хватает данных, мы прибегаем к оценочным суждениям. Рассуждать о любого рода оценках можно только в контексте вероятностей; законы вероятности – основа оценки». Это слова Шерманна Кента, офицера спецслужб США, которого многие считают «отцом-основателем» национальной разведывательной сводки.
Работать с вероятностями сложно именно потому, что законы вероятности, как заметил Хант, часто кажутся нелогичными, а сделанные на основе этих законов выводы чаще всего кажутся нестрогими и расплывчатыми.
Прежде чем мы перейдем к более детальному обсуждению вероятности и помня об этой неопределенности и расплывчатости, давайте выполним следующее упражнение.
Упражнение 31. Медвежатник (1)
В сейфе, за пятью дверьми, каждая из которых заперта на замок с кодом, хранится великолепный бриллиант. Вы грабитель и хотите его украсть. У всех пяти дверей идентичные кодовые замки, произведенные одной и той же компанией, но коды, разумеется, разные. Вам приходилось сталкиваться с такими замками ровно десять раз – и только однажды, в последний раз из этих десяти, вы не смогли вскрыть замок. Исходя исключительно из характеристик замка и не принимая в расчет никаких других факторов, оцените в процентах (20, 50, 80 % и так далее), какова вероятность того, что вы сможете открыть все пять дверей и украсть бриллиант? Запишите свой ответ, в процентах, на листе бумаги.

Рядом с полученной цифрой запишите, как вы бы охарактеризовали свою оценку: скажем, «маловероятно», «возможно», «очень вероятно», «почти наверняка».

Как правило, люди, почти не задумываясь, используют выражения, указывающие на вероятность: «скорее всего», «наверняка», «возможно», «шансов мало», «определенно» – и ошибочно полагают, что все вокруг понимают эти слова одинаково.
– Каковы шансы, что мы успеем на встречу, если вначале пообедаем? – спрашивает жена мужа.
– Есть шансы, – отвечает тот.
– Хорошо, давай тогда зайдем сюда.
Они опаздывают на встречу на полчаса. Жена расстроена и упрекает мужа:
– Я думала, ты сказал, что мы успеем!
Он крайне удивлен:
– Я не говорил ничего подобного.
– Ты же сказал, что шансы есть.
– Ну да, но я имел в виду, что скорее всего мы не успеем!
К сожалению, мы совершенно по-разному понимаем значение формулировок (прилагательных и наречий), указывающих на вероятность. Задайте нескольким людям вопрос: что именно означает слово «вероятно», если выразить его в процентах, – и получите варианты от 55 до 85 %. Что значит «небольшая вероятность дождя»? Люди понимают это как вероятность от 1 до 15 %. Если не верите моим оценкам, проверьте сами. Спросите членов семьи или друзей, какое именно численное выражение имеют, по их мнению, типичные словосочетания, используемые для выражения вероятности. Получите массу неожиданных и весьма любопытных ответов.
Анализируем ли мы проблему в одиночку или сообща с другими, мы должны придерживаться строгого правила: выделять все вероятностные суждения и обязательно выражать их численно, в процентах, а не словами. В приведенном ниже отрывке из статьи в журнале Firehouse я выделил курсивом некоторые слова, чтобы вы поняли, что я имею в виду.
В ходе реализации программы работы с малолетними поджигателями, разработанной в Главном управлении пожарной охраны США, выяснилось, что максимальная доля поджогов устраивается детьми в возрасте от пяти до девяти лет. Данные, полученные в ходе выполнения программы, указывают также на то, что в целом пяти-шестилетние дети могут и не осознавать, что от одной спички иногда сгорает целый дом. Таким образом, малолетние дети оказываются не только в группе максимального риска в отношении поджога, но становятся и наиболее вероятными жертвами при пожаре… В отличие от детей младшего школьного возраста, которые с некоторой вероятностью могут становиться причиной одного-двух случаев поджога в отсутствие взрослых, психически нездоровые люди с гораздо большей вероятностью оказываются замешанными в нескольких случаях поджога. Пожар, устроенный ребенком, страдающим психическим расстройством, с большой вероятностью оказывается настолько серьезным, что требуется вызов пожарной бригады.
Этот текст – типичный пример использования словосочетаний, указывающих на вероятностные оценки. Если бы я их не выделил курсивом, мы бы их даже не заметили при чтении. Но, так как они в значительной степени определяют смысл текста, стоит выяснить, о какой именно величине вероятности идет речь в каждом из случаев.
…шестилетние дети могут и не осознавать, что от одной спички иногда сгорает целый дом.
Какая вероятность подразумевается под этим «могут»? Пятьдесят процентов? Десять процентов? Один процент? А ведь это крайне важно. Если вероятность того, что шестилетний американец не понимает, какова опасность даже одной подожженной спички, составляет 50 %, то можно утверждать, что в целом жилища американцев находятся в серьезной опасности. А если вероятность того, что ребенок в этом возрасте еще не осознает, что от одной спички может случиться пожар, всего 1 %, то опасность следует признать гораздо менее серьезной.
…малолетние дети… становятся и наиболее вероятными жертвами при пожаре.
Что в данном случае означает «наиболее вероятными»? Шестьдесят процентов? Восемьдесят? Девяносто девять?
Повторю: на этапе анализа, работая с проблемой или готовя отчет, мы должны все вероятностные оценки выражать в процентах. Но не используйте проценты в итоговом документе – если только (а это бывает редко) ваши цифры не основаны на достоверных фактах и точных расчетах. Самое сложное при работе с вероятностью – переход от словесных оценок к численным, в виде процентов. Но это скорее тема для книги о том, как писать аналитические документы, а не о структурировании процесса анализа. (Один из подходов, которым вовсю пользуются одни авторы и который полностью отвергают другие, заключается в том, чтобы в самом начале текста определить, что именно означают оценочные вероятностные суждения, применяемые в книге: скажем, «вполне возможно» – 85 %, «вряд ли» – 20 % и так далее)
Определение вероятности
Как определить вероятность? Для этого существует два основных способа: расчет или повторяемость опыта. Если у нас имеются все необходимые факты, то есть все данные, как в проблеме детерминированного типа, мы можем рассчитать вероятность. А если мы не располагаем всеми фактами, то можем оценить вероятность, исходя из частоты событий. Повторяемость – это частота появления определенного события в прошлом; опыт – это то, что происходит в ходе события. Простой пример: если я брошу на пол десять лампочек одну за другой и все они разобьются, какова вероятность, что и одиннадцатая тоже разобьется? Очень высокая! Почти 100 %! Как я пришел к этому выводу? Частота: я повторяю событие десять раз. Опыт: лампочки бьются во всех повторяемых событиях.
Очевидно, что чем больше нам известно об обстоятельствах события, вероятность которого нам требуется определить, тем точнее наша оценка. Что же делать, если мы знаем крайне мало или вовсе ничего? Что если кто-то попросил нас оценить, какая из трех политических партий выиграет выборы в африканской Танганьике? Если вы совершенно случайно не занимаетесь изучением Африки, то не сможете сделать никаких предположений. Французский маркиз Пьер-Симон де Лаплас (1749–1827) предложил способ оценки в таких ситуациях. Согласно Лапласу, если мы пытаемся определить, вероятность какого из двух событий выше, но не имеем фактов, на основе которых можно было бы сделать оценку, нужно считать, что все события одинаково вероятны. Повторю: если мы не располагаем фактами, указывающими на то, что из нескольких рассматриваемых событий одно вероятнее других, следует предположить, что вероятность наступления всех возможных событий одинакова.
К счастью, мы редко оказываемся в ситуациях, когда приходится прибегать к принципу Лапласа. Почти всегда в ходе анализа ситуации мы замечаем сходство с прошлыми событиями, о которых хотя бы кое-что знаем, и можем использовать это знание как основу для оценки вероятностей. Однако наши оценки подвержены влиянию всех тех ограничений и особенностей мышления, о которых я уже рассказывал. Мы находим «сходство с прошлыми событиями», исходя из придуманных нами же закономерностей, которые разум склонен находить даже там, где их нет. А так как мы склонны большее внимание уделять событиям, которые согласуются с предпочтительным для нас исходом ситуации, то мы считаем, что вероятность таких событий выше, чем тех, которые не соответствуют нашим интересам или нашему взгляду на ситуацию. И даже сталкиваясь с противоречащими нашей теории фактами, мы продолжаем настаивать на своем. Так что в силу особенностей мышления наши оценки вероятности событий действительно могут в значительной степени не соответствовать реальности.
Широко известный пример склонности завышать вероятность желательного для нас исхода событий – печально известное заявление одного из руководителей британского военно-морского флота, принимавшего участие в высадке в Нормандии в ходе Второй мировой войны: «Не думаю, что кто-то из нас осознавал тогда степень опасности. Никто не собирался погибнуть в Нормандии: мы шли, чтобы сражаться и победить. Уверен, что никто из погибших не предполагал, что этот день может стать для него последним». Завышение или занижение вероятности исхода, который в наибольшей степени соответствует нашим намерениям, – типичный результат самообольщения: со мной этого не случится, потому что я этого не хочу. Как говорил Фрэнсис Бэкон, мы предпочитаем верить в то, что предпочитаем считать истиной.
В ходе анализа проблем данные о вероятности различных событий играют важнейшую роль, поэтому мы должны подходить к оценке вероятностей крайне аккуратно.
Типы вероятностных событий
Два наиболее распространенных типа событий, вероятность которых мы пытаемся оценить в ходе анализа проблем, – взаимоисключающие и взаимозависимые.
К взаимоисключающим относятся такие события, наступление одного из которых исключает наступление прочих. К таким можно отнести, например, результаты подбрасывания монеты. Так как у монеты две стороны, то каждый из результатов (орел или решка) исключает другой. Когда мы бросаем обычный кубик с цифрами, результаты тоже взаимоисключающие. У стандартного кубика восемь сторон, и всякий раз выпадает только одна, исключая выпадение всех прочих. Результаты выборов тоже взаимоисключающие – да и почти все решения, которые нам приходится принимать: выбирая одно, мы исключаем другое.
К взаимозависимым относятся такие события, наступление одного из которых зависит от наступления другого. Такие события формируют последовательность. Хороший пример подобной цепочки событий – начало работы автомобильного двигателя. Мы вставляем ключ в замок зажигания, поворачиваем его, в результате чего стартер начинает вращать двигатель, и тот заводится. Двигатель не заведется, если его не начать вращать; стартер не начнет работу, если мы не повернем ключ зажигания; мы не сможем повернуть ключ, пока не вставим его в замок. Первое событие – ключ вставлен в замок зажигания – условие для второго, то есть второе может наступить только при условии, что произошло первое. Второе событие обусловливает третье и так далее.
Вероятность взаимоисключающих событий
Как рассчитать вероятность взаимоисключающих событий? Объяснять это удобно на примере банки, в которой лежит 90 конфет: 45 красных, 36 желтых и девять зеленых. Мы опускаем руку в банку и вытаскиваем конфету. Этот процесс можно даже визуализировать с помощью дерева сценариев (рис. 13.1): у нас есть три возможных и взаимоисключающих исхода, означающих, что мы вытаскиваем красную, желтую или зеленую конфету.
Рис. 13.1
Предположим, что конфеты распределены в банке случайным образом. Какова тогда вероятность того, что, запустив руку внутрь нее, мы не глядя вытащим красную конфету? Какова вероятность вытащить желтую? А зеленую?
В случае взаимоисключающих событий можно оценивать вероятность их наступления в процентах. К примеру, вероятность вытащить красную конфету из 90, лежащих в банке, равна доле красных конфет среди этих 90. Понятно? Возможно, будет понятнее, если я перефразирую: если 30 % конфет в банке красные, то вероятность вытащить именно красную конфету, запустив руку в банку лишь один раз, равна 30 %.
Как же рассчитать долю красных конфет в банке? Я использую традиционный подход, который освоил еще в школе и считаю самым наглядным способом структурировать решение (да, это еще один способ структурирования). Для расчета сформулируем простой вопрос: какой процент составляет число х от числа y? А потом делим х на y, то есть делим на то, процент от чего хотим рассчитать. К примеру, какой процент составляет 3 от 6? Делим 3 на 6, получаем 0,5, или 50 %.
Эта формула особенно удобна, когда контекст проблемы не позволяет быстро определить, что на что делить. Меня учили, что в этом случае как раз и нужно рассуждать упрощенно: что есть часть, а что – целое. Вот, скажем: в бушеле 40 яблок, из которых десять гнилые. Какова доля гнилых яблок? Некоторым может быть сложно сразу решить, что должно быть в числителе и что в знаменателе. Для этого просто перефразируйте задачу: какую долю от 40 составляет 10? То есть какой процент составляет 10 от 40? И сразу понятно: 10 / 40 = 0,25, или 25 %. Прекрасно! (Господи, благослови моих школьных учителей.)
Упражнение 32. Конфеты (1)
Давайте используем нашу формулу и рассчитаем, какова в процентах доля красных, желтых и зеленых конфет в банке. Сделайте подсчеты и запишите результат.

Вот что у вас должно было получиться:
• красные: какую долю от 90 составляет 45? 45 / 90 = 0,5, или 50 %;
• желтые: какую долю от 90 составляет 36? 36 / 90 = 0,4, или 40 %;
• зеленые: какую долю от 90 составляет 9? 9 / 90 = 0,1, или 10 %.
Теперь давайте переведем проценты в вероятности и запишем цифры на нашем дереве сценариев (рис. 13.2).
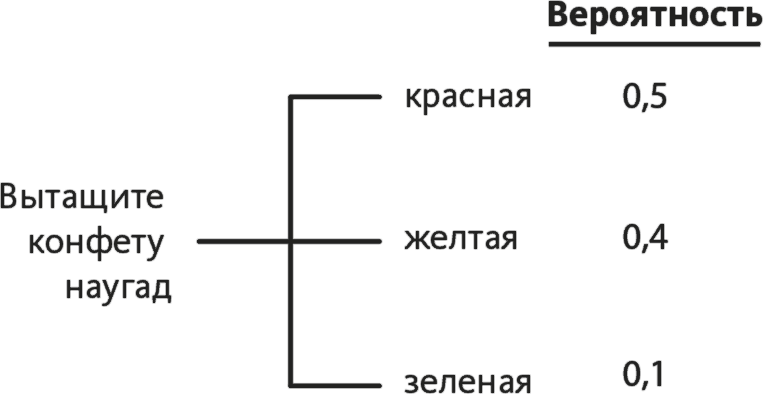
Рис. 13.2
Так как это дерево содержит вероятности, я предлагаю называть его дерево вероятностей.
Дерево вероятностей
Дерево вероятностей обладает всеми свойствами дерева сценариев и имеет еще одну особенность: оно позволяет нам анализировать весь набор событий с точки зрения вероятностей, то есть оценивать, какой из сценариев наиболее или наименее вероятен и какие решения и события в рамках каждого из альтернативных сценариев более или менее вероятны. Из дерева сценариев мы видим лишь, что может или чего не может произойти, – а дерево вероятностей показывает, какие события более или менее вероятны. Добавление к анализу нового параметра, вероятности, приближает наши рассуждения и заключения к реальной жизни.
Дерево вероятностей помогает сфокусироваться на тех решениях и событиях, которые и определяют вероятность наиболее важных для нас сценариев: проверять допущения и предположения, собирать дополнительные факты. Мы можем по своему усмотрению менять вероятность каждого из решающих факторов: такой анализ называется сенситивным, или анализом чувствительности. Дерево вероятностей подсказывает нам, на каких решениях или событиях необходимо сфокусировать внимание, если мы хотим повысить вероятность того или иного сценария. Представляете, какое это преимущество: вы теперь можете рассчитать, на чем именно нужно сконцентрировать усилия, чтобы получить желаемый результат.
При построении дерева вероятностей необходимо строго придерживаться трех приведенных ниже правил.
1. Как и в случае с деревом сценариев, события должны быть взаимоисключающими, то есть каждое из них должно быть самостоятельным и независимым от других.
2. Совокупность событий должна быть исчерпывающей, то есть включать все возможные варианты.
3. Суммарная вероятность событий каждой из ветвей дерева должна равняться единице.
Тем, кто редко сталкивается с численной оценкой вероятностей, важно помнить, что событие не может произойти большее количество раз, чем указывает его вероятность. Вероятность не может превышать 100 %, или единицы.
Давайте немного усложним задачу про конфеты.
Какова вероятность вытащить красную или зеленую конфету, засунув руку в банку один раз?
Чтобы решить эту задачу, давайте рассуждать в процентах: каков процент красных или зеленых конфет в банке? У нас 45 красных и девять зеленых, то есть всего 54 такие конфеты. Какой процент от 90 составляет 54? Считаем: 54 / 90 = 0,6. То есть вероятность вытащить за один раз зеленую или красную конфету составляет 60 %. Мы сложили вероятности вытащить красную (0,5) или зеленую (0,1) конфеты.
Упражнение 33. Конфеты (2)
Какова вероятность вытащить за один раз красную или желтую конфету? Какова вероятность вытащить желтую или зеленую? Запишите ответы на листке бумаги.

Вероятность вытащить красную или желтую конфету: 0,5 + 0,4 = 0,9.
Вероятность вытащить желтую или зеленую конфету: 0,4 + 0,1 = 0,5.
Важно понимать: наше «или» означает необходимость сложить вероятности отдельных событий. Многие этого не осознают, пока как следует не разберутся, из чего я делаю вывод, что такая концепция человеку интуитивно не очевидна. И даже после объяснения многие этот принцип понимают не до конца. Как писал Кэмпбелл, люди не запоминают правил расчета вероятности, даже когда применяют их для решения задач. Поэтому большинству из нас нужно всякий раз выводить эти правила заново.
Давайте попрактикуемся: построим дерево вероятностей и рассчитаем вероятности.
Упражнение 34. Лиса в курятнике
В курятнике 50 кур: десять рыжих, пять черных, 15 коричневых, 20 белых. Если лиса проберется в курятник и наугад схватит одну из куриц, какова вероятность того, что ей попадется рыжая или коричневая курица? На листе бумаги постройте дерево вероятностей, отметьте на нем кур всех типов, посчитайте вероятность того, что лиса схватит курицу каждого из цветов по отдельности, а затем ответьте на вопрос задачи.

На рис. 13.3 показано дерево вероятностей.

Рис. 13.3
Вероятность поймать рыжую курицу составляет 0,2, вероятность поймать коричневую – 0,3. Поэтому вероятность поймать рыжую или коричневую курицу составляет 0,2 + 0,3 = 0,5.
Вероятность взаимосвязанных событий
Как рассчитывается вероятность взаимосвязанных событий? Перемножением вероятностей всех этих событий. Сейчас я объясню, почему это так.
Какова вероятность, что при подбрасывании монеты два раза подряд выпадет орел?
На рис. 13.4 представлено дерево вероятностей, иллюстрирующее все возможные последовательности событий. Вероятность, что при первом броске выпадет орел, равна 0,5. Если выпадает решка, эксперимент заканчивается, так как нам нужно, чтобы орел выпал два раза подряд. Поэтому второй раз мы бросаем монету, только если в первый раз выпал орел. То есть второй бросок зависит от результата первого: между этими событиями существует взаимосвязь. Если в первый раз выпадает орел, то какова вероятность, что и во второй раз выпадет орел? По-прежнему 0,5. То есть мы получаем 50 %-ную вероятность от 50 %-ной вероятности (0,5 умножить на 0,5), что два раза подряд выпадет орел. Вероятность наступления этих двух последовательных событий равна 0,25.

Рис. 13.4
Давайте рассчитаем вероятность взаимосвязанных событий на примере задачи с конфетами. Какова вероятность того, что мы вытащим вначале красную конфету (и вернем ее в банку), а сразу за ней зеленую? Цепочка событий представлена на рис. 13.5. Вероятность вытащить красную конфету равна 0,5; вероятность вытащить зеленую конфету, без привязки к красной, – 0,1. Поэтому вероятность вытащить красную, а потом зеленую конфету равна 0,5 × 0,1 = 0,05.
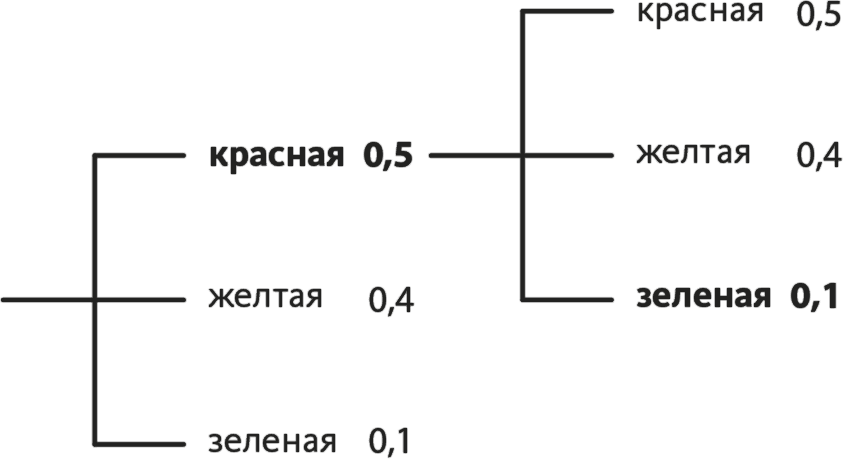
Рис. 13.5
Упражнение 35. Медвежатник (2)
Давайте вернемся к нашей задаче о взломщике сейфов. Вам нужно пройти через пять дверей, в каждой из которых кодовый замок. Вы вор, и уже девять раз из десяти вам удавалось верно подобрать код к такому замку; только на десятый раз вы не справились. Какова вероятность того, что вы сможете открыть все пять дверей?
Здесь требуется расчет вероятности взаимосвязанных событий, потому что вы перейдете ко второй двери, только если откроете первую, а к третьей – только если откроете вторую, и так далее.
Какова вероятность (В1) того, что вы сможете пройти через первую дверь? Мы можем рассчитать вероятность, исходя из ваших прежних результатов: девять из десяти. Какую долю от 10 составляет 9? 90 %, то есть В1 = 0,9.
Какова вероятность открыть и первую, и вторую двери? Возможность открыть вторую дверь зависит от того, открыли ли вы первую. Таким образом, мы должны умножить вероятность открыть первую дверь (0,9) на вероятность открыть вторую дверь. Думаете, вероятность открыть вторую дверь тоже 0,9? Нет, ответ неверный. Это была вероятность открыть первую дверь, которую мы рассчитали, исходя из того, что в прошлом вы смогли открыть 9 дверей из 10. Но после того как вы открыли первую из этих пяти дверей, ваш результат изменился: в совокупности вы успешно открыли уже 10 дверей из 11. То есть вероятность открыть вторую дверь составляет 10 / 11 = 0,91. Тогда вероятность открыть и первую, и вторую двери равна 0,9 × 0,91 = 0,82. Пока все понятно? Если нет, вернитесь к началу этого объяснения и перечитайте.
Рассчитайте вероятность того, что вы сможете открыть пятую дверь и украсть бриллиант. Запишите расчеты и ответ.

Предлагаю вам решение задачи:
В1 = 9 / 10 = 0,9;
В2 = 0,9 × (10 / 11) = 0,82;
В3 = 0,82 × (11 / 12) = 0,75;
В4 = 0,75 × (12 / 13) = 0,69;
В5 = 0,69 × (12 / 14) = 0,64.
Сравните 0,64 с со сделанным вами выше предположением о том, какова вероятность, что вы сможете украсть бриллиант. Насколько близка ваша оценка к расчету? Большинство склонны считать, что вероятность открыть все пять дверей и добраться до бриллианта довольно высока. Если вы ошиблись в оценке вероятности в задаче , не огорчайтесь: как я уже говорил, вероятность кажется большинству из нас одной из наиболее сложных для понимания и применения концепций. Ее совершенно невозможно понять интуитивно. Поэтому важно разобраться, чем отличаются взаимоисключающие и взаимосвязанные события и их вероятности, и как можно больше практиковаться в расчетах вероятности. Только так оценка вероятности станет понятной и привычной.
Разница между расчетом взаимоисключающих и взаимосвязанных событий особенно четко проявляется в том, как мы изображаем эти два вида расчетов на дереве вероятностей.
Чтобы определить вероятность двух или более событий, представляющих собой результат одного события или решения (ситуация «или – или»), мы складываем вероятность каждого из них. Чтобы определить вероятность одного или более взаимосвязанных и происходящих одно за другим событий (ситуация «и…, и…»), перемножаем вероятности каждого из них.
Отвечая на вопросы, требующие оценки вероятности, нужно тщательно читать формулировку вопроса, чтобы понять, относится он к единственному возможному событию (из числа взаимоисключающих событий) или к серии взаимосвязанных событий. Формулировка вопроса всегда критически важна. Необходимо уметь переформулировать задачу так, чтобы однозначно понять, в чем именно заключается вопрос.
Шесть шагов работы с деревом вероятностей
Шаг 1: определить задачу.
Шаг 2: определить, какие основные решения и события нужно проанализировать.
Шаг 3: построить дерево сценариев, отразив на нем все существенные альтернативные варианты.
А. Проверить, что все решения/события каждой ветви дерева – взаимоисключающие.
В. Проверить, что все решения/события каждой ветви в совокупности – всеобъемлющие.
Шаг 4: оценить вероятность каждого решения/события. Сумма вероятностей каждой ветви должна равняться единице.
Шаг 5: рассчитать условную вероятность каждого из сценариев.
Шаг 6: найти ответы на поставленные вопросы, связанные с вероятностью решений/событий.
Давайте выполним упражнение, в котором необходимо будет рассчитать вероятность и взаимоисключающих, и взаимосвязанных событий.
Упражнение 36. Ракетный снаряд Karati
Разработчики ракетного снаряда Karati должны успеть к сроку, назначенному Министерством обороны. Для этого им нужно начать производство снарядов в течение двух ближайших месяцев. Критически важный тестовый запуск ракеты запланирован на завтра, и у него возможны три результата (вероятность каждого указана в скобках):
1) полный провал (0,2);
2) успешный старт, затем технический сбой (0,6);
3) полный успех (0,2).
В случае если запуск закончится полным провалом, вероятность того, что разработчикам удастся начать производство в течение двух ближайших месяцев, составит лишь 0,1. Если старт пройдет успешно, но за ним последует технический сбой, то вероятность запуска производства в ближайшие два месяца составит 0,4. В случае полного успеха вероятность запуска производства в ближайшие два месяца составит 0,9.
Постройте дерево вероятностей, отражающее все указанные события. Затем ответьте на следующие вопросы:
1) какова вероятность того, что разработчики смогут уложиться в отведенный срок?
2) какова вероятность того, что они не уложатся в отведенный срок, если тестовый запуск окажется полностью провальным или если старт пройдет успешно, но затем последует технический сбой?

В конце книги . Чтобы ответить на поставленные вопросы, нам нужно вначале рассчитать вероятность выполнения проекта в срок в рамках цепочки взаимосвязанных событий по шести возможным сценариям: «Провал тестового запуска – Запуск производства, да»; «Провал тестового запуска – Запуск производства, нет» и так далее. Для этого перемножим вероятности соответствующих исходов тестового запуска и запуска производства и запишем результаты у соответствующих ветвей дерева «Вероятность выполнить проект в срок». Чтобы ответить на вопрос 1, нам нужно сложить вероятности трех взаимоисключающих событий ветвей «Да» (0,02 + 0,24 + 0,18 = 0,44). Чтобы ответить на вопрос 2, сложим две вероятности ветвей «Нет» сценариев «Полный провал» и «Технический провал» (0,18 + 0,36 + 0,02 = 0,56).
Вы наверняка заметите, что при сложении вероятности выполнения и невыполнения проекта в срок дают единицу, как и должно быть; вероятности по каждой ветви дерева в сумме должны равняться единице. Складывая вероятности и получая в сумме единицу, вы лишний раз проверяете, что расчеты проведены верно.
Предлагаю вам еще одно упражнение, в котором нужно рассчитать вероятности обоих видов.
Упражнение 37. Угон самолета (1)
Вы член банды террористов, намеренных угнать пассажирский самолет, чтобы добиться освобождения нескольких ваших товарищей, попавших в тюрьму в одной из зарубежных стран. Ваш вожак попросил вас рассчитать вероятность того, что в результате угона самолета террористов освободят из тюрьмы.
Постройте дерево вероятностей, отразив следующее:
• успешность или провал угона;
• попытку (да или нет) антитеррористической группы спасти взятых в заложники пассажиров и членов экипажа;
• успешность или провал попытки спасти пассажиров и членов экипажа;
• вероятность гибели пассажиров или членов экипажа (никто не погиб; некоторые погибли; погибли все) во время операции по спасению заложников.
Вы провели тщательный анализ ситуации и определили, что вероятность того, что будет проведена операция по спасению заложников, составляет 0,9. Вероятность того, что погибнут все пассажиры и члены экипажа, составляет 0,1; вероятность того, что не погибнет никто, составляет 0,1; вероятность того, что погибнут некоторые из заложников, составляет 0,8. Вероятность того, что ваших товарищей выпустят, если все погибнут, составляет 0; вероятность того, что ваших товарищей выпустят, если не погибнет никто или погибнут лишь некоторые, составляет 0,1. Вероятность того, что ваших товарищей освободят, если операции по спасению не будет вовсе, составляет 0,9.
Рассчитайте вероятность того, что все арестованные террористы будут освобождены.

В я предлагаю свою версию дерева вероятностей. Чтобы определить вероятность того, что все арестованные террористы будут освобождены, я вначале умножил вероятности трех взаимосвязанных событий («Предпринята попытка спасения заложников», «В ходе операции по спасению погибли все пассажиры и экипаж», «Террористы освобождены»).
Затем я сложил результаты сценария «Освобождены – да» (0,72 + 0,009 + 0,09 = 0,171). Чтобы убедиться, что суммарная вероятность по каждой ветке равна единице, я прибавил к этой сумме результат сценария «Освобождены – нет» (0,829); в результате сложения (0,829 + 0,171) я действительно получил единицу.
Упражнение 38. Новые продукты
Производитель электронного оборудования должен принять решение, стоит ли инвестировать в исследования и разработки новой линейки продуктов. Рассматриваются две альтернативы:
1) выпуск сотовых телефонов с миниатюрным экраном и возможностями компьютера;
2) небольшие портативные антенны для приема сигнала коммерческих спутниковых телеканалов.
Для проведения анализа ключевыми будут четыре фактора, перечисленные ниже.
1. Потребуется ли для выпуска нового продукта переоборудование сборочной линии.
2. Будет ли необходимое переоборудование линии полным или частичным.
3. Придется ли проводить обучение нынешних сотрудников или нанимать новых для работы на переналаженной линии сборки.
4. Если потребуется переоборудование, то неизбежны дополнительные расходы либо на подготовку нынешних рабочих, либо на привлечение новых. Насколько серьезным будет рост расходов на рабочую силу? Если переоборудования не потребуется, расходы на персонал сохранятся на прежнем уровне.
В табл. 13.1 показаны вероятности для каждого из факторов. Основываясь на этих данных, постройте два дерева вероятностей: одно для выпуска телефонов, другое для выпуска антенн. Ответьте на перечисленные вопросы по каждому из продуктов, то есть отдельно для телефонов и антенн.
Таблица 13.1

1. Какова вероятность, что линию сборки придется полностью переоборудовать?
2. Какова вероятность, что нынешних рабочих придется дополнительно обучать?
3. Какова вероятность, что компании придется нанимать новых рабочих?
4. Какова вероятность, что расходы на рабочую силу вырастут незначительно?
5. Какова вероятность, что расходы на рабочую силу вырастут значительно?

В я привожу два дерева вероятностей.
В я предлагаю ответы на вопросы.
Подведем итоги
Когда нам не хватает данных, мы вынуждены прибегать к оценкам. Оценочные суждения формулируются в терминах вероятностей, а законы вероятности становятся основой для этих формулировок.
Вероятность – одна из наиболее важных концепций, описанных в этой книге, потому что анализ всегда основан на вероятностных оценках. При этом большинство из нас крайне плохо понимают концепцию вероятности: работать с вероятностями сложно, потому что сами законы вероятности часто противоречат привычной нам логике.
Людям трудно правильно применять правила расчета вероятностей.
Несмотря на наличие сложного математического аппарата и научно обоснованных концепций, люди часто оценивают вероятности событий, опираясь на субъективные ощущения, а не на расчеты. Как и во многих других случаях, эти субъективные оценки напрямую зависят от предубеждений и прочих особенностей мышления.
Большинство из нас способны интуитивно оценить вероятность лишь в простейших задачах.
Мы определяем вероятность двумя способами: либо на основе расчетов, если располагаем необходимыми для этого данными, либо, если данных нет, то исходя из повторяемости опыта.
Чаще всего при расчете вероятности мы имеем дело либо со взаимоисключающими событиями (типа «или – или», когда вероятности отдельных событий складываются), либо со взаимосвязанными событиями (типа «и… и…», когда вероятности перемножаются).
При необходимости оценить вероятность одного или более альтернативных исходов, когда мы не располагаем данными о том, какой из них более вероятен, нужно следовать принципу Лапласа и считать, что вероятность всех возможных исходов одинакова. Вообще мы редко оказываемся в ситуации, когда данных для такой оценки нет.
Вероятности рассматриваемых альтернатив мы отображаем на дереве вероятностей, при создании которого нужно руководствоваться тремя принципами: отражаемые события должны быть взаимоисключающими (то есть каждое из них отделено от других); совокупность событий должна быть всеобъемлющей (то есть дерево должно отражать все возможные исходы); вероятности событий на каждой ветке дерева должны в сумме давать единицу.
Все мы очень по-разному понимаем смысл слов и выражений, указывающих на вероятность, поэтому лучше выражать вероятностные оценки с помощью цифр. Важно также помнить, что, видя оценку вероятности, выраженную в процентах и долях, мы чаще всего предполагаем, что эти цифры точны и основаны на тщательно проведенном анализе, что не всегда соответствует действительности. Поэтому использовать проценты и доли в отчетах о проведенном анализе проблемы нужно крайне осторожно и ответственно.
Назад: Глава 12 Адвокат дьявола
Дальше: Глава 14 Дерево анализа полезности

