Книга: Как не ошибаться. Сила математического мышления
Назад: Глава семнадцатая Общественное мнение? Нет такого
Дальше: Эпилог Как быть правым
Глава восемнадцатая
«Я создал странный новый мир из ничего!»
Кондорсе считал, что на вопросы типа «Кто самый лучший лидер?» обязательно найдется какой-то правильный ответ, а граждане – что-то вроде прибора для научных исследований таких вопросов. Конечно, полной уверенности нет, поскольку подобный метод грешит некоторой неточностью измерений, но в среднем подлинности оценок граждан доверять можно. В понимании Кондорсе, демократия и принцип большинства – способ не ошибаться, благодаря математике.
В наше время мы уже так не говорим о демократии. Сегодня для большинства людей привлекательность демократического выбора состоит в его справедливости. Мы говорим на языке прав человека и, руководствуясь соображениями морали, верим в то, что люди должны иметь возможность выбирать своих правителей, даже если их выбор не всегда бывает мудрым.
Это не просто дискуссия о политике – здесь вопрос фундаментальный, применимый к любой области психической деятельности. Мы пытаемся понять, что соответствует истине, или определить, какие умозаключения позволяют нам устанавливать существующие правила и процедуры. К счастью, эти понятия обычно приходят к соглашению, однако настоящие трудности, а вместе с ними и все самое концептуально интересное происходят там, где они расходятся.
Возможно, вы считаете очевидным, что именно поиск истины и есть то, чем мы должны заниматься. Однако так бывает не всегда и особенно в уголовном праве, где расхождения налицо: есть совершившие преступление обвиняемые, но им нельзя вынести приговор (хотя бы потому, что доказательства получены с нарушениями); есть невиновные, осужденные за преступление, которого они не совершали. Что можно считать справедливым в этом случае – наказать виновного и освободить невиновного или придерживаться принципов уголовного судопроизводства, к чему бы это ни привело? В экспериментальной науке мы уже видели дискуссию между Рональдом Фишером с одной стороны и Ежи Нейманом и Эгоном Пирсоном – с другой. Нужно ли нам, как считал Фишер, пытаться понять, какие гипотезы мы должны считать истинными? Или нужно придерживаться философии Неймана и Пирсона, согласно которой следует воздерживаться от размышлений об истинности гипотез и вместо этого ставить вопрос следующим образом: какие гипотезы необходимо признать корректными согласно выбранным нами правилам вывода, независимо от того, истинны они или нет?
Мы сталкиваемся с такими проблемами и в математике, которая считается обителью определенности, причем сталкиваемся не в дебрях каких-то загадочных современных исследований, а в старой доброй классической геометрии. Эта тема присутствует даже в аксиомах Евклида, о которых шла речь в предыдущей главе. Пятая аксиома гласит:
Если P – это точка, а L – прямая, которая не проходит через Р, существует только одна прямая, проходящая через точку Р и параллельная прямой L.
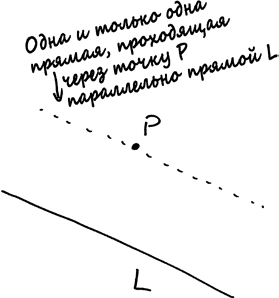
Забавно, не правда ли? На самом деле эта аксиома несколько более сложная и менее очевидная, чем остальные. Во всяком случае, так ее воспринимали геометры на протяжении многих столетий. Считается, что сам Евклид испытывал неприязнь к этой аксиоме, доказав первых двадцать восемь теорем, представленных в «Началах», с использованием только первых четырех аксиом.
Неизящная аксиома – как пятно в углу на полу: мешать не мешает, но с ума сводит, и вы тратите уйму времени, чтобы истребить его, вымыть пол, сделав его снова чистым и красивым. В математическом контексте это сводилось к попыткам показать, что пятая аксиома, так называемый постулат о параллельности, вытекает из всех остальных аксиом. Если это было бы так, проблему пятой аксиомы можно было бы удалить из списка Евклида, оставив его безупречно чистым.
После двух тысяч лет чистки пятно все еще оставалось на своем месте.
Венгерский математик Фаркаш Бойяи, который всю жизнь безуспешно пытался решить эту задачу, в 1820 году посоветовал сыну Яношу не следовать по этому пути:
Ты не должен пытаться одолеть теорию параллельных линий на этом пути; я знаю этот путь, я проделал его до конца, я пережил эту беспросветную ночь, и всякий светоч, всякую радость моей жизни я в ней похоронил. Мало того, оставь в покое учение о параллельных линиях… Я был готов сделаться мучеником этой истины, чтобы только очистить геометрию от этого пятна, чтобы передать роду человеческому безукоризненную науку. Я проделал ужасную гигантскую работу; я достиг много лучшего, нежели то, что было получено до меня; но совершенного удовлетворения не получил… Я отказался от этого, когда понял, что ни один человек не способен достичь дна этой тьмы. Я оставил эти попытки без всякого утешения, жалея себя и все человечество. Извлеки урок из моего примера.
Сыновья не всегда прислушиваются к советам отцов, а математики не всегда легко бросают то, чем занимаются. Младший Бойяи продолжил работать над параллельными прямыми, и в 1823 году у него было готово в общем виде решение этой древней задачи. Он написал отцу ответное письмо, в котором было сказано следующее:
Я открыл нечто столь удивительное, что был потрясен, и было бы величайшим несчастьем, если это было бы утеряно. Когда ты, мой дорогой отец, увидишь это, ты все поймешь; сейчас же я могу сказать только одно: я создал странный новый мир из ничего.
Гениальная идея Яноша Бойяи состояла в том, чтобы взглянуть на эту задачу под другим углом. Вместо того чтобы пытаться вывести постулат о параллельности из других аксиом, он позволил своему разуму поставить вопрос так: что если аксиома о параллельных прямых ошибочна? Следует ли из этого противоречие? Янош Бойяи пришел к выводу, что ответ на этот вопрос отрицательный и что существует другая геометрия (не геометрия Евклида, а нечто иное), в которой первые четыре аксиомы верны, а постулат о параллельности – нет. Следовательно, постулат о параллельности не может быть доказан на основании первых четырех аксиом, поскольку такое доказательство исключило бы возможность геометрии Бойяи. Но эта геометрия существует.
Иногда то или иное математические открытие «витает в воздухе»: по едва понятным причинам сообщество ученых готово к очередному достижению, поэтому оно приходит из нескольких источников одновременно. В то время, когда Бойяи в Австро-Венгрии разрабатывал свою неевклидову геометрию, Николай Лобачевский делал то же самое в России. А великий Карл Фридрих Гаусс, старый друг старшего Бойяи, сформулировал много аналогичных идей в работе, которая до сих пор не опубликована. (Когда Гауссу сообщили о публикации Бойяи, он отреагировал несколько неучтиво: «Хвалить это было бы равносильно тому, чтобы хвалить себя».)
Для описания так называемой гиперболической геометрии Бойяи, Лобачевского и Гаусса понадобится намного больше книжного пространства, чем у нас осталось. Однако, как отметил Бернхард Риман несколько десятилетий спустя, существует более простая неевклидова геометрия, которую нельзя назвать безумным новым миром. Речь идет о геометрии сферы.
Давайте вспомним первые четыре аксиомы:
• существует прямая, соединяющая любые две Точки;
• любой отрезок Прямой можно расширить до отрезка Прямой любой требуемой длины;
• для любого отрезка Прямой L есть Окружность с радиусом L;
• все Прямые Углы равны между собой.
Наверное, вы обратили внимание на то, что я внес в описание этих аксиом некоторые изменения, написав термины точка, прямая, окружность и прямой угол с прописной буквы. Я сделал это не ради имитации старинного издания, а чтобы подчеркнуть, что с сугубо логической точки зрения не имеет значения, как обозначены «точки» и «прямые». Мы вольны назвать их лягушками и кумкватами, но структура логического вывода из этих аксиом осталась бы прежней. Это напоминает плоскость Джино Фано из семи точек, на которой «прямые» выглядят совсем не так, как нас учили в школе, однако это не имеет значения: весь смысл в том, что эти прямые ведут себя как прямые согласно законам геометрии. В каком-то смысле было бы даже лучше называть точки лягушками, а прямые кумкватами, поскольку это позволило бы нам избавиться от предвзятого мнения по поводу значений слов Точка и точка, Прямая и прямая.
Вот что означают эти термины в сферической геометрии Римана. Точка – это пара точек на сфере, которые являются антиподальными, или диаметрально противоположными друг другу. Прямая – это большая окружность – другими словами, окружность на поверхности сферы, а отрезок прямой – это отрезок такой окружности. Окружность – это и есть окружность, которая теперь может иметь любой размер.
При таких определениях первые четыре аксиомы Евклида верны! Для любых двух точек (то есть любых двух пар антиподальных точек на сфере) существует прямая (другими словами, большая окружность), которая их соединяет. Более того (хотя это и не одна из аксиом), любые две прямые пересекаются в одной точке.
У вас могут быть претензии ко второй аксиоме: как мы можем утверждать, что отрезок прямой можно продолжить до любой длины, если он не может быть длиннее самой прямой, которая является окружностью сферы? Это вполне обоснованное возражение, но все сводится к вопросу интерпретации. В понимании Римана в аксиоме идет речь о неограниченных, а не о бесконечно протяженных прямых. Между этими двумя понятиями есть едва уловимое различие: прямые Римана, которые являются окружностями, имеют конечную длину, но они не ограничены, то есть по ним можно передвигаться бесконечно, не останавливаясь.
И наконец пятая аксиома – совсем другая история. Предположим, у нас есть точка Р и прямая L, не содержащая точку P. Есть ли одна и только одна прямая, проходящая через точку Р, параллельная L? Нет, по очень простой причине: в сферической геометрии нет такой штуки, как параллельные прямые! Любые две большие окружности на сфере должны пересекаться.
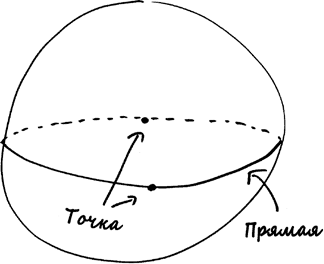
Доказательство на один абзац. Любая большая окружность С делит сферу на две равные части, каждая из которых имеет одну и ту же площадь; обозначим эту площадь символом А. Теперь допустим, что существует еще одна большая окружность C', параллельная окружности С. Поскольку окружность C' не пересекается с окружностью С, она должна быть полностью расположена с одной или другой стороны С, на одной из полусфер с площадью А. Но это означает, что площадь, ограниченная окружностью C', меньше площади А, что невозможно, поскольку каждая большая окружность ограничивает область, площадь которой равна в точности А.
Следовательно, постулат о параллельности опровергается самым эффектным образом. (В геометрии Бойяи ситуация прямо противоположная. Существует слишком много параллельных прямых: в действительности не просто две, а бесконечное множество прямых проходят через Р параллельно L. Как вы догадываетесь, такую геометрию трудно визуализировать.)
Если вам кажется знакомым столь странное утверждение, что две прямые не могут быть параллельными, то причина в том, что мы уже сталкивались с чем-то подобным. Это тот же феномен, что и в случае проективной плоскости, которую Брунеллески и его друзья-художники использовали для разработки теории перспективы. Там также любые две прямые пересекались. И это не случайное совпадение: геометрия точек и прямых Римана – это то же самое, что и геометрия проективной плоскости.
Если интерпретировать пять аксиом в виде утверждений по поводу точек и прямых на сфере, первые четыре аксиомы верны, а пятая нет. Если бы пятая аксиома была логическим следствием первых четырех аксиом, существование сферы представляло бы противоречие: пятая аксиома была бы и истинной (в силу истинности первых четырех аксиом), и нет (в силу того, что мы знаем о сферах). Согласно старому доброму доказательству от противного это означает, что сфер не существует. Но сферы все же существуют, а значит, пятую аксиому невозможно вывести из первых четырех аксиом. Что и требовалось доказать.
На первый взгляд может показаться, что для выведения этого пятна с пола понадобилось слишком много времени и труда. Однако мотивация для доказательства утверждений такого рода заключена не просто в одержимости эстетикой (хотя я не могу отрицать тот факт, что такие чувства играют определенную роль). Дело вот в чем: как только становится понятным, что первые четыре аксиомы применимы ко многим разным геометриям, тогда любая теорема, доказанная Евклидом на основании этих аксиом, должна быть истинной не только в евклидовой геометрии, но и во всех остальных геометриях, в которых верны эти аксиомы.
И эти теоремы касаются не просто абстрактных геометрий, созданных только ради того, чтобы доказать какую-то мысль. В постэйнштейновскую эпоху мы понимаем, что неевклидова геометрия – не просто игра. Нравится вам это или нет, но именно так в действительности выглядит пространственно-временной континуум.
Такая история повторяется в области математики снова и снова: мы разрабатываем метод, применимый к решению одной задачи, и, если это хороший метод (то есть метод, содержащий поистине новую идею), в большинстве случаев мы обнаруживаем, что то же самое доказательство работает во многих ситуациях, которые могут отличаться от исходной ситуации в такой же мере, в какой сфера отличается от плоскости, или даже больше. В настоящее время молодой итальянский математик Оливия Карамелло создает настоящую сенсацию своими заявлениями, что теории, которые управляют различными областями математики, по сути своей тесно взаимосвязаны друг с другом (если вы отдаете предпочтение формальным терминам, они «классифицированы в соответствии с одними и теми же топосами Гротендика»). Следовательно, теоремы, которые доказаны в одной области математики, можно спокойно перенести в другую область, которая кажется на первый взгляд совершенно иной. Сейчас слишком рано говорить, удалось ли Карамелло создать «странный новый мир», как это сделал Бойяи, но ее работа в значительной степени согласуется с давней традицией в математике, частью которой был Бойяи.
Эта традиция обозначается термином «формализм». Именно об этом говорил Годфри Гарольд Харди, когда с восхищением отметил, что математики XIX столетия начали наконец спрашивать «как определить 1 − 1 + 1 − 1 +…», а не «что есть 1 − 1 + 1 − 1 +…». Это позволяло им избежать «ненужных затруднений», преследовавших математиков более ранних времен. Согласно самой чистой версии этой точки зрения, математика становится своего рода игрой с участием символов и слов. Утверждение можно считать теоремой, если его выводят из аксиом посредством логических операций. Но что к чему отсылают аксиомы и теоремы, что они означают – этим пусть занимается кто-то другой. Что такое Точка, Прямая, лягушка или кумкват? Это может быть все, что ведет себя так, как того требуют аксиомы, а смысл можно выбирать, исходя из текущих потребностей. Сугубо формальная геометрия – это геометрия, которой можно заниматься, даже если вы никогда не видели или не представляли себе точку или прямую; это геометрия, в которой не имеет значения, как на самом деле выглядят точки и прямые в обычном их понимании.
Безусловно, Харди посчитал бы душевные страдания Кондорсе совершенно лишними. Он посоветовал бы ему пытаться выяснить не то, кто в действительности самый лучший кандидат или даже кого избиратели на самом деле хотели бы видеть на соответствующей должности, а скорее, какого кандидата мы должны определить как выбор народа. И такой формалистский подход к демократии получил достаточно большое распространение в современном свободном мире. Во время президентских выборов в штате Флорида в 2000 году, результаты которых были оспорены в суде, тысячи избирателей округа Палм-Бич, которые были убеждены в том, что голосуют за Альберта Гора, на самом деле отдали свои голоса за кандидата от палеоконсервативной Партии реформ Патрика Бьюкенена из-за некорректного оформления «бюллетеня-бабочки». Если Гор получил бы эти голоса, он победил бы на выборах в штате Флорида и стал бы президентом США.
Однако Гор не получил эти голоса; на самом деле он даже не боролся за них всерьез. Наша избирательная система носит формалистский характер: значение имеет отметка, сделанная на бюллетене, а не то, о чем думает избиратель, когда делает эту отметку. У Кондорсе вызвали бы обеспокоенность и те люди, которые проголосовали за Ральфа Нейдера. При условии (которое кажется вполне допустимым), что большинство этих людей отдавали предпочтение Гору перед Бушем, именно Гор является тем кандидатом, который должен был выиграть выборы согласно аксиоме Кондорсе: большинство избирателей предпочитали Гора Бушу, а еще более значительное большинство отдавали ему предпочтение перед Нейдером. Однако все эти предпочтения не играют никакой роли в действующей избирательной системе. Мы определяем волю народа как отметку, которая чаще всего появляется на листах бумаги, собранных в кабинках для голосования.
Безусловно, даже это количество можно оспорить. Как подсчитывать бюллетени, в которых перфорируемое отверстие пробито не полностью? Что делать с результатами голосования, переданными по почте с зарубежных военных баз, если нет возможности удостовериться, что эти голоса были отданы избирателями в день выборов или накануне? И в какой степени в округах штата Флорида следовало провести пересчет избирательных бюллетеней в попытке как можно более точно определить результаты голосования?
Последний вопрос был передан на рассмотрение Верховного суда США, где судьи приняли окончательное решение по данному делу. Команда Гора обратилась с просьбой о повторном подсчете голосов в некоторых округах, и Верховный суд штата Флорида дал свое согласие, однако Верховный суд США отменил это решение, зафиксировав результаты выборов, согласно которым Буш одержал победу с перевесом 537 голосов. Дальнейший подсчет, по всей видимости, привел бы к более точному учету голосов, но это, по мнению суда, не является высшей целью выборов. Члены суда заявили, что пересчитывать голоса в некоторых округах было бы несправедливо по отношению к тем избирателям, голоса которых повторно не подсчитывались. Задача государства не в том, чтобы подсчитать голоса как можно точнее (то есть знать, что произошло на самом деле), а в том, чтобы подчиняться формальному протоколу, который говорит нам (в терминах Харди), кого следует определить в качестве победителя.
В более общем смысле формализм в области права проявляется в виде строгого следования процедуре и букве закона даже в тех случаях, когда (или особенно когда) они на первый взгляд противоречат тому, что предписывает здравый смысл. Судья Антонин Скалиа, самый ярый сторонник правового формализма, говорит об этом очень откровенно: «Да здравствует формализм. Именно он делает государственную власть властью законов, а не властью людей».
По мнению Скалиа, когда судьи пытаются понять, что подразумевает закон (его дух), их неизбежно вводят в заблуждение собственные предубеждения и предпочтения. Лучше строго придерживаться буквы конституции и законов, обращаясь с ними как с аксиомами, из которых судебные решения можно выводить посредством чего-то вроде логической дедукции.
В области уголовного права Скалиа демонстрирует такую же приверженность формализму: истина по определению представляет собой то, что считает таковым судебный процесс, проведенный надлежащим образом. Скалиа на удивление четко описывает эту позицию в своем особом мнении по делу Троя Энтони Дэвиса за 2009 год, в котором он утверждал, что убийце, которого признали виновным, не следует предоставлять право на новое судебное слушание доказательств даже в случае, если семь из девяти свидетелей по этому делу отказались от своих показаний:
Этот суд никогда не исходил из того, что конституция запрещает исполнение приговора в отношении подсудимого, который был признан виновным в результате полного и справедливого судебного разбирательства, но которому впоследствии удалось убедить суд, рассматривающий законность ареста, в том, что он «действительно» невиновен (слово никогда выделено курсивом, а слово действительно взято в кавычки самим Скалиа. – Д. Э.).
Скалиа утверждает, что, с точки зрения суда, значение имеет только вердикт жюри присяжных. Дэвис был убийцей независимо от того, убил он кого-то или нет.
Судья Джон Робертс не такой ярый сторонник формализма, как Скалиа, но в целом он симпатизирует философии коллеги. Во время слушания по вопросу об утверждении обвинений он в 2005 году, как стало известно, описал свою работу в бейсбольных терминах:
Судьи – это слуги закона, а не наоборот. Судьи подобны арбитрам. Арбитры не устанавливают правила, а применяют их. Роль арбитра и судьи крайне важна. Они следят за тем, чтобы все играли по правилам. Но эта роль ограничена. Никто никогда не ходил на бейсбольный матч, чтобы посмотреть на арбитра.
Робертс, сознательно или нет, повторил слова Билла Клема, арбитра Национальной лиги бейсбола, сказавшего: «Матч с лучшим судейством – такой матч, после которого болельщики не могут вспомнить работавших на нем арбитров».
Однако роль арбитра не настолько ограничена, как ее подавали Робертс и Клем, поскольку бейсбол – это формалистский вид спорта. Чтобы понять это, достаточно проанализировать первый матч чемпионата Американской лиги бейсбола между командами «Балтимор Ориолс» и «Нью-Йорк Янкиз», который проходил в Бронксе. Команда Балтимора выигрывала во второй половине восьмого иннинга, когда шорт-стоп «Янкиз» Дерек Джитер запустил длинный флайбол на правую сторону поля неподалеку от реливера «Ориолс» Армандо Бенитеса. Это был хороший хит, но доступный для центр-филдера Тони Тараско, который уже занял позицию и был готов принять мяч. В этом момент двенадцатилетний болельщик «Янкиз» Джеффри Майер, который сидел на трибуне в первом ряду, протянул руку через забор и толкнул мяч на трибуну.
Джитер знал, что это не хоумран. Тараско и Бенитес знали, что это не хоумран. Пятьдесят шесть тысяч болельщиков «Янкиз» тоже знали, что это не хоумран. Единственным человеком на стадионе «Янки», который не видел, как Майер протянул руку через забор, оказался самый важный человек, арбитр Рич Гарсия. Гарсия назвал эту ситуацию хоумраном. Джитер даже не попытался исправить решение арбитра и уж тем более пробежаться по базам и сравнять счет. Никто от него этого и не ожидал по той простой причине, что бейсбол – это формалистский вид спорта. Ситуация такова, какой ее объявляет арбитр, не более того. Или, как это сформулировал Клем в самом откровенном утверждении онтологических взглядов, когда-либо предпринятом должностным лицом из области профессионального спорта: «Это ничто, пока я это не назову».
Ситуация постепенно меняется. Начиная с 2008 года арбитрам разрешено просматривать видеоповторы в тех случаях, когда они не уверены в том, что происходило на поле на самом деле. Это хорошо, поскольку позволяет принимать правильные решения вместо неправильных, но многие давние любители бейсбола считают, что новшество чуждо духу этого вида спорта. Я отношусь к их числу. Бьюсь об заклад, Джон Робертс также.
Не все разделяют взгляды Скалиа на закон (кстати, заметьте, что его мнение по делу Дэвиса оказалось в меньшинстве). Как мы видели в деле «Аткинс против штата Виргиния», имеющиеся в конституции формулировки, такие как «жестокое и необычное наказание», оставляют довольно места для интерпретации. Если даже великий Евклид оставил некоторую неопределенность в своих аксиомах, как мы можем ждать чего-то другого от создателей конституции? Реалисты из области права, такие как судья и профессор Чикагского университета Ричард Познер, утверждают, что правовая практика Верховного суда – это ни в коем случае не упражнение в формальном следовании правилам, как заявляет Скалиа:
Большинство случаев, на рассмотрение которых Верховный суд дает свое согласие, – это лотерея в том смысле, что они не могут быть решены посредством традиционного правового обоснования с его упором на формулировки конституции и законодательных актов, а также на ранее принятые решения. Если эти дела можно было бы решить посредством таких, по сути, семантических методов, они вне всяких сомнений решались бы на уровне Верховного суда штата или федерального апелляционного суда и никогда не передавались бы на повторное рассмотрение в Верховный суд.
Согласно этой точке зрения, трудные правовые вопросы, то есть те дела, которые передаются в Верховный суд, – это вопросы, которые не определены аксиомами. Следовательно, судьи находятся в том же положении, в котором был Паскаль, когда обнаружил, что не может обосновать свой способ получения любого вывода о существовании Бога. Тем не менее единственное, что нам остается, по замечанию Паскаля, – играть в эту игру. Суд должен решить, делать ли ему это в соответствии с традиционным способом построения юридических рассуждений или нет. Иногда суд идет по пути Паскаля: если такие рассуждения не позволяют вынести вердикт, следует принять решение, которое повлечет за собой самые лучшие последствия. По мнению Познера, именно по этому пути пошли члены Верховного суда, в числе которых был и Скалиа, в процессе рассмотрения дела «Буш против Гора». Познер утверждает, что принятое Верховным судом решение на самом деле не было обосновано ни конституцией, ни судебным прецедентом. Это было решение, принятое из прагматических соображений: избежать угрозы многомесячного избирательного хаоса.
Призрак противоречия
Формализму свойственна строгая элегантность, представляющая интерес для таких людей, как Годфри Гарольд Харди, Антонин Скалиа и я сам, которые получают истинное удовольствие от красивой строгой теории, не допускающей никаких противоречий. Однако нелегко неизменно придерживаться принципов такого рода, да и не совсем понятно, целесообразно ли это. Даже судья Скалиа время от времени признавал, что, когда буква закона требует принятия абсурдных решений, от буквальных формулировок необходимо отказаться в пользу правдоподобного предположения по поводу того, что имел в виду Конгресс. Аналогичным образом ни один ученый не хочет быть строго ограниченным правилами статистической значимости, о каких бы принципах ни шла речь. Когда вы проводите два эксперимента, один из которых тестирует курс лечения, кажущийся теоретически многообещающим, а другой проверяет, демонстрирует ли дохлый лосось эмоциональную реакцию на показанные ему фотографии, и оба эксперимента дают успешный результат с р-значением 0,03, на самом деле вам не следует одинаково обращаться с этими двумя гипотезами. Вы должны оценивать абсурдные выводы с повышенным скептицизмом, и к черту правила.
Величайшим сторонником формализма в математике был немецкий математик Давид Гильберт; его список двадцати трех проблем, представленный в Париже, на Международном конгрессе математиков в 1900 году, определил направление развития математики на большую часть ХХ столетия. Гильберт – математик, вызывающий такое глубокое почтение, что любая работа, имеющая хотя бы косвенное отношение к его проблемам, приобретает особый блеск даже сто лет спустя. Однажды я познакомился с историком немецкой культуры из Колумбуса (штат Огайо), который рассказал мне, что именно склонность Гильберта носить сандалии с носками объясняет тот факт, что этот стиль до сих пор достаточно популярен среди математиков. Я не нашел никаких свидетельств, что это действительно так, но мне нравится так считать, поскольку это позволяет составить правильное представление о масштабе его влияния.
Значительное количество проблем Гильберта было вскоре решено; другие проблемы, например под номером восемнадцать – о максимально плотной упаковке сфер, – были решены только недавно. Некоторые проблемы до сих пор остаются нерешенными, и многие математики активно пытаются найти их решение. В частности, за решение проблемы под номером восемь (доказательство гипотезы Римана) Фонд Клэя выплатит вознаграждение в размере одного миллион долларов. Минимум в одном случае великий Гильберт ошибся. В проблеме под номером десять он предложил найти алгоритм, позволявший взять любое уравнение и определить, есть ли у него решение, при котором все переменные принимают целочисленные значения, но в 1960–1970-е годы математики Мартин Дэвис, Юрий Матиясевич, Хилари Патнэм и Джулия Робинсон опубликовали ряд работ, в которых было доказано, что такого алгоритма не существует. (Специалисты по теории чисел вздохнули с облегчением: было бы немного досадно, если оказалось бы, что некий формальный алгоритм способен автоматически решать задачи, на которые мы тратим столько лет.)
От всех остальных проблем Гильберта отличалась проблема под номером два. В ней был сформулирован не столько математический вопрос, сколько вопрос об отношении к самой математике. Свое описание этой задачи Гильберт начал с безоговорочной поддержки формалистского подхода к математике:
Занимаясь исследованием основ науки, мы должны сформировать систему аксиом, содержащую точное и исчерпывающее описание связей, существующих между элементарными понятиями этой науки. Выстроенные таким образом аксиомы являются вместе с тем определениями этих элементарных понятий; при этом ни одно утверждение в области той науки, основы которой мы изучаем, нельзя считать правильным до тех пор, пока оно не будет выведено из этих аксиом посредством конечного числа логических операций.
К тому времени, когда Гильберт выступал в Париже с докладом, он уже пересмотрел аксиомы Евклида и переписал их так, чтобы исключить любые следы неопределенности; при этом он неукоснительно придерживался принципа полного вытеснения геометрической интуиции. Его версия этих аксиом действительно сохраняет свой смысл даже в случае, если заменить точки и прямые лягушками и кумкватами. Сам Гильберт говорил об этом так: «Следует добиться того, чтобы с равным успехом можно было говорить вместо точек, прямых и плоскостей о столах, стульях и пивных кружках». Одним из первых приверженцев новой геометрии был молодой Абрахам Вальд, который еще во время учебы в Вене показал, что некоторые аксиомы Гильберта можно вывести из других, а значит, без них можно обойтись.
Гильберт не хотел ограничиваться геометрией. Он мечтал создать сугубо формальную математику, в которой заявление, что утверждение истинно, было бы равноценно заявлению, что это утверждение подчиняется изначально установленным правилам – ни больше, ни меньше. Такая математика понравилась бы Антонину Скалиа. Аксиомы, которые Гильберт планировал использовать в арифметике и которые впервые сформулировал итальянский математик Джузеппе Пеано, на первый взгляд не кажутся тем, в отношении чего могут возникать интересные вопросы или разногласия. Эти аксиомы содержат утверждения такого рода: «Ноль – это число», «Если x равно y, а y равно z, тогда х равно z» и «Если число, непосредственно следующее за числом x, тождественно числу, непосредственно следующему за числом y, тогда числа x и y тождественны». Все эти истины мы считаем самоочевидными.
Аксиомы Пеано интересны тем, что на основании этих малейших отправных точек можно создать серьезные математические построения. На первый взгляд сами аксиомы касаются только целых чисел, но даже Пеано показал, что, начав с аксиом и двигаясь дальше посредством определения и логической дедукции, можно определить рациональные числа и их основные свойства. После того как в XIX столетии было обнаружено, что общепринятые определения в математическом анализе и геометрии логически неполноценны, мир математики охватил кризис и смятение. Гильберт воспринимал формализм как способ начать все с чистого листа, опираясь при этом на фундаментальную, абсолютно непреложную основу.
Однако программу Гильберта преследовал призрак – призрак противоречия. Представьте себе такой кошмарный сценарий. Члены математического сообщества, работая в тесном сотрудничестве друг с другом, перестраивают весь аппарат теории чисел, геометрии и исчисления, начиная с фундаментальных аксиом, и кирпичик за кирпичиком выстраивают новые теоремы, прикрепляя каждый новый уровень к предыдущему с помощью правил дедукции. А затем однажды математик из Амстердама приводит доказательство того, что определенное математическое утверждение истинно, тогда как другой математик из Киото приводит доказательство того, что это не так.
Что теперь? Начав с утверждений, которые невозможно поставить под сомнение, мы пришли к противоречию. Следует ли из этого вывод, что аксиомы ошибочны? Или что ошибка содержится в структуре самого логического вывода? А что делать с десятилетиями работы, основанной на этих аксиомах?
Таким образом, вторая проблема в списке проблем, которые Гильберт представил перед собравшимися в Париже математиками, была сформулирована так:
Однако прежде всего я хотел бы обозначить следующее как самый важный среди многочисленных вопросов, которые можно поставить в отношении аксиом: доказать, что они непротиворечивы, другими словами, – что конечное число основанных на них логических рассуждений не может привести к получению противоречивых результатов.
У кого-то возникнет искушение заявить, что подобное просто не может произойти. Разве это возможно? Ведь очевидно, что аксиомы истинны. Однако для древних греков было не менее очевидным, что геометрическая величина должна представлять собой соотношение двух целых чисел: такими были их представления о математике до тех пор, пока теорема Пифагора и упорно иррациональный квадратный корень из двух не разрушили эту систему понятий. Математике свойственна скверная привычка демонстрировать, что время от времени то, что кажется очевидно истинным, оказывается абсолютно ошибочным. Возьмем в качестве примера хотя бы Готлоба Фреге – немецкого логика, который, подобно Гильберту, не покладая рук трудился над укреплением логических основ математики. В центре внимания Фреге была не теория чисел, а теория множеств. Он также начал с последовательности аксиом, которые казались настолько очевидными, что их вряд ли нужно было формулировать. В теории множеств Фреге множество представляло собой не что иное, как совокупность объектов, называемых элементами. Для обозначения множеств, в которые входят определенные элементы, обычно используются фигурные скобки {}. Так, {1, 2, поросенок} – это множество, элементами которого являются число 1, число 2 и поросенок.
Когда некоторые элементы множества обладают определенным свойством, а другие нет, такое множество представляет собой совокупность элементов с указанным свойством. Давайте сформулируем это немного проще: существует множество поросят, и среди них есть желтые поросята, которые образуют множество желтых поросят. Здесь трудно с чем-то не согласиться. Однако эти определения носят весьма обобщенный характер. В качестве множества может выступать совокупность поросят, действительных чисел, идей, возможных вселенных или других множеств. И именно последний случай создает множество проблем. Существует ли множество множеств? Безусловно. А множество всех бесконечных множеств? Почему бы нет? На самом деле оба эти множества обладают любопытным свойством: они являются элементами самих себя. В частности, множество бесконечных множеств – это, разумеется, само по себе бесконечное множество, элементы которого содержат множества такого типа:
{целые числа}
{целые числа, а также поросенок}
{целые числа, а также Эйфелева башня}
и так далее, и тому подобное. Очевидно, что этому нет конца.
Мы могли бы назвать такое множество уроборическим, по имени мифического змея, который кусает себя за хвост и пожирает сам себя. Следовательно, множество бесконечных множеств является уроборическим, но множество {1, 2, поросенок} нет, поскольку ни один из его элементов не является множеством {1, 2, поросенок}: все его элементы – это либо числа, либо животные, но не множества.
Теперь наступает кульминационный момент. Путь NO – это множество всех неуроборических множеств. NO – достаточно странная концепция, чтобы представить ее себе, но, если определение Фреге допускает это в мире множеств, мы тоже должны сделать это.
Является ли NO уроборическим множеством или нет? Другими словами, является ли NO элементом NO? Согласно определению, если NO – это уроборическое множество, тогда NO не может входить в состав NO, которое состоит только из неуроборических множеств. Но утверждать, что NO не является элементом NO, – это равносильно утверждению о том, что NO – это неуроборическое множество, то есть оно не содержит себя.
Но подождите-ка: если NO – это неуроборическое множество, тогда это элемент множества NO, которое является множеством всех неуроборических множеств. Выходит, что NO – это все же элемент NO, то есть NO – уроборическое множество.
Если NO – уроборическое множество, оно таковым не является, а если это не уроборическое множество, то оно является таковым.
Примерно таким было содержание письма, которое молодой Бертран Рассел написал Фреге в июне 1902 года. Рассел познакомился с Пеано в Париже на Международном конгрессе. Неизвестно, присутствовал ли он на докладе Гильберта, но он безусловно был сторонником программы сведения всей математики к чистой последовательности выводов из базовых аксиом. Письмо Рассела начинается как письмо молодого почитателя к старшему логику: «Я согласен с вами по всем основным моментам, особенно с вашим неприятием психологического элемента в логике и с тем значением, которое вы придаете концептуальному обозначению основ математики и формальной логике, которую, кстати говоря, трудно распознать».
Но затем Рассел пишет следующее: «У меня возникла трудность только с одним вопросом».
Далее он объясняет в письме, в чем состоит проблема с множеством NO, которая известна теперь как парадокс Рассела.
В конце письма Рассел выражает свое сожаление по поводу того, что Фреге еще не опубликовал второй том своего труда «Grundgesetze der Arithmetik» («Основные законы арифметики»). На самом деле эта книга была завершена и уже находилась в печати, когда Фреге получил письмо Рассела. Несмотря на уважительный тон («У меня возникла трудность» вместо «Я только что испортил труд всей вашей жизни»), Фреге сразу же понял, что означает парадокс Рассела для его версии теории множеств. Менять что-то в книге было слишком поздно, но Фреге поспешно добавил эпилог с объяснением губительного озарения Рассела. Пожалуй, это объяснение Фреге можно считать самым грустным предложением о математике из всех, которые когда-либо были написаны: «Einem wissenschaftlichen Schriftsteller kann kaum etwas Unerwünschteres begegnen, als dass ihm nach Vollendung einer Arbeit eine der Grundlagen seines Baues erschüttert wird». Что означает: «Вряд ли ученый может столкнуться с чем-либо более нежелательным, чем разрушение самой основы только что законченной работы».
Гильберт и другие формалисты не хотели оставлять открытой возможность противоречия, встроенного в аксиомы подобно часовой бомбе; он стремился разработать математическую систему, в которой непротиворечивость была бы гарантирована. Нельзя сказать, что Гильберт на самом деле считал, будто в арифметике может быть скрыто противоречие. Подобно большинству математиков и даже большинству обычных людей, он был убежден, что стандартные правила арифметики – это истинные утверждения о целых числах, а значит, они не могут противоречить друг другу. Однако этого было недостаточно, поскольку в основе такого подхода лежало предположение о том, что множество целых чисел действительно существует. Для многих это было камнем преткновения. За несколько десятилетий до этого Георг Кантор впервые поставил концепцию бесконечности на твердую математическую основу. Однако его работа не получила широкого принятия и распространения; кроме того, была довольно большая группа математиков, которые считали, что любое доказательство, основанное на существовании бесконечных множеств, должно считаться сомнительным. Все готовы были принять тот факт, что существует число 7. Однако существование множества всех чисел оставалось спорным вопросом. Гильберт прекрасно знал, что сделал Рассел с Фреге, и осознавал, какие опасности таят в себе поверхностные рассуждения о бесконечных множествах. «Внимательный читатель, – писал он в 1926 году, – обнаружит, что в книгах по математике полно глупости и абсурда, источником которых является бесконечность». (Тон этого высказывания был бы вполне уместным в каком-нибудь из наиболее яростных мнений судьи Антонина Скалиа.) Гильберт искал финитное доказательство непротиворечивости, то есть доказательство, в котором не было бы никаких ссылок на бесконечные множества и в которое рациональный ум не мог бы не поверить.
Однако Гильберта ждало разочарование. В 1931 году Курт Гёдель доказал свою знаменитую вторую теорему о неполноте, которая гласила, что не существует финитного доказательства непротиворечивости арифметики. Он погубил программу Гильберта одним ударом.
Так следует ли вам беспокоиться по поводу того, что завтра после обеда может наступить коллапс всей математики? Как бы там ни было, меня это не беспокоит. Я действительно верю в бесконечные множества и считаю доказательства непротиворечивости, в которых используются бесконечные множества, достаточно убедительными, чтобы спокойно спать по ночам.
Большинство математиков считают так же, как и я, но есть и те, кто придерживается другого мнения. В 2011 году логик из Принстонского университета Эдвард Нельсон представил доказательство непротиворечивости арифметики. (К счастью для нас, через несколько дней Терри Тао обнаружил в этом доказательстве ошибку.) Владимир Воеводский, лауреат Филдсовской премии, который работает сейчас в Институте перспективных исследований в Принстоне, произвел в 2010 году сенсацию, заявив, что не видит никаких оснований для того, чтобы считать арифметику непротиворечивой. Вместе с большой группой коллег со всего мира Воеводский предложил новое обоснование математики. Гильберт начинал с геометрии, но быстро пришел к пониманию того, что непротиворечивость арифметики – это более фундаментальная проблема. Напротив, группа Воеводского утверждает, что по большому счету именно геометрия имеет фундаментальное значение – не такая геометрия, которая была бы привычной для Евклида, а современная геометрия, называемая «теория гомотопий». Смогут ли эти основы устоять перед скептицизмом и противоречиями? Спросите меня об этом через двадцать лет. Такие вещи требуют времени.
Модель математики Гильберта уцелела после кончины его формалистской программы. Еще до публикации работы Гёделя Гильберт ясно дал понять, что в его намерения не входит создание математики сугубо формалистским способом. Это было бы слишком трудно! Даже если геометрию можно представить в виде осуществления манипуляций с бессмысленными последовательностями символов, ни один человек не в состоянии генерировать геометрические идеи, не рисуя при этом картинки, не представляя себе фигуры и не размышляя о геометрических объектах как о реальных вещах. Как правило, мои друзья философы считают эту точку зрения, обычно называемую платонизмом, довольно сомнительной: разве может быть реальным пятнадцатимерный гиперкуб? Я могу сказать только то, что для меня такие вещи так же реальны, как, например, горы. В конце концов, я могу определить пятнадцатимерный гиперкуб. А можете ли вы определить гору?
Однако все мы отпрыски Гильберта; когда по выходным мы пьем пиво вместе с философами и философы начинают атаковать нас вопросами по поводу статуса объектов, которые мы изучаем, мы возражаем им, укрываясь в своей формалистской цитадели: безусловно, мы прибегаем к геометрической интуиции, для того чтобы понять, что происходит, однако наш окончательный вывод по поводу истинности того, о чем мы говорим, опирается на формальное доказательство, лежащее в основе происходящего. Согласно известной формулировке Филипа Дэвиса и Рубена Херша, «типичный практикующий математик – платонист по будним дням и формалист по воскресеньям».
Гильберт не стремился разрушить платонизм; он хотел сделать мир безопасным для платонизма, водрузив такие объекты, как геометрия, на столь незыблемую основу, что мы могли бы чувствовать себя на протяжении недели такими же морально сильными, как и в воскресенье.
Гениален не человек, гениально то, что он делает
Я много говорил о роли Гильберта, и это правильно, однако существует опасность, что, уделяя так много внимания именам ведущих математиков, я способствую созданию ошибочного представления о математике как об области, в которой немногочисленные одинокие гении, отмеченные печатью еще в момент рождения, прокладывают остальному человечеству путь, по которому оно сможет двигаться дальше. Легко рассказывать историю, придерживаясь такого подхода. В некоторых случаях, как в случае со Шринивасой Рамануджаном, это не так уж далеко от истины. Рамануджан был одаренным ребенком из южных районов Индии, с самого детства генерировавшим удивительно оригинальные математические идеи, которые он сам называл божественными откровениями богини Намагири. На протяжении многих лет он работал в полной изоляции от остального математического мира, имея доступ только к нескольким книгам, которые могли познакомить его с современным состоянием этой дисциплины. К 1913 году, когда Рамануджан наконец установил контакт с большим миром теории чисел, он уже исписал много тетрадей примерно четырьмя тысячами теорем, многие из которых до сих пор являются предметом активных исследований. (Богиня открывала Рамануджану формулировки теорем, но не давала никаких доказательств – их предстоит искать нам, преемникам Рамануджана).
Однако Рамануджан был особым человеком, историю которого рассказывают так часто именно в силу ее нетипичности. Гильберт начинал как очень хороший, но не исключительный студент, который ни в коей мере не был самым блестящим молодым математиком в Кёнигсберге; таковым был Герман Минковский – на два года моложе Гильберта. Впоследствии Минковский сделал весьма серьезную математическую карьеру, но так и не достиг высот Гильберта.
Один из самых мучительных аспектов преподавания математики – видеть, как культ гениальности причиняет вред студентам. Культ гениальности внушает студентам мысль о том, что заниматься математикой не стоит, если ты не самый лучший в области математики, поскольку только вклад избранных гениев имеет значение. Но ведь мы не обращаемся так ни с одной другой дисциплиной! Я никогда не слышал, чтобы студенты говорили: «Мне нравится “Гамлет”, но мне не место на курсе углубленного изучения английского; я не тот парень, который сидит в первом ряду, знает все пьесы и начал читать Шекспира в девятилетнем возрасте!» Спортсмены не бросают занятия спортом только потому, что один из членов команды показывает более высокие результаты. Тем не менее я вижу, как многообещающие молодые математики каждый год уходят, несмотря на то что любят математику, потому что кто-то в их поле зрения в чем-то их «превосходит».
Так мы теряем многих студентов, выбравших математику в качестве профилирующей дисциплины, а значит, мы теряем много будущих математиков. Однако это еще не вся проблема. Думаю, нам нужно больше изучающих математику студентов, которые не станут математиками. Нам нужно больше врачей, учителей средней школы, генеральных директоров и сенаторов, хорошо знающих математику. Однако мы не получим всего этого до тех пор, пока не отбросим стереотип, который гласит, что математикой стоит заниматься только молодым гениям.
Кроме того, культ гениальности приводит к недооценке тяжелого труда. Когда я начинал свою карьеру, я считал, что слово «трудолюбивый» – это своего рода завуалированное оскорбление и что так говорят о студенте, которого трудно назвать умным. Однако способность усердно трудиться (сфокусировать все свое внимание и энергию на той или иной задаче, целенаправленно размышляя над ней снова и снова и анализируя все, что напоминает решение, несмотря на отсутствие внешних признаков прогресса) – такое качество свойственно далеко не всем. Без такого качества, которое психологи называют в наши дни упорством, невозможно заниматься математикой. Без него легко потерять из виду важность работы, поскольку математическое вдохновение, когда оно наконец все же приходит, может показаться бессильным и преходящим. Я хорошо помню, как доказал свою первую теорему. Во время учебы в университете я работал над первой дипломной работой и совершенно зашел в тупик. Однажды вечером я был на заседании редколлегии университетского литературного журнала, пил красное вино и время от времени принимал участие в обсуждении какого-то скучного рассказа, как вдруг у меня в голове все перевернулось, и я понял, как преодолеть барьер. Не было никаких деталей, но это и не имело значения: в глубине души я не сомневался, что задача решена.
Именно так протекает процесс математического творчества. Вот как вспоминает французский математик Анри Пуанкаре о большом геометрическом открытии, которое он сделал в 1881 году:
…по прибытии в Кутанс мы взяли омнибус для прогулки; и вот в тот момент, когда я заносил ногу на ступеньку омнибуса, мне пришла в голову идея – хотя мои предыдущие мысли не имели с нею ничего общего, – что те преобразования, которыми я воспользовался для определения фуксовых функций, тождественны преобразованиям неевклидовой геометрии. Я не проверил этой идеи; для этого я не имел времени, так как, едва усевшись в омнибус, я возобновил начатый разговор, тем не менее я сразу почувствовал полную уверенность в правильности идеи. Возвратясь в Кан, я проверил; идея оказалась правильной.
Однако Пуанкаре подчеркивает, что на самом деле это произошло не на ступеньке омнибуса. Тот момент вдохновения был результатом многих недель труда, как осознанного, так и подсознательного, который каким-то образом готовит разум к установлению необходимых связей между различными идеями. Сидеть и ждать вдохновения – это путь к неудаче, каким бы талантливым молодым человеком вы ни были.
Возможно, мне трудно обосновать эту точку зрения, поскольку я сам был одним из одаренных детей. Я знал, что стану математиком, с тех пор как мне исполнилось шесть лет. Я изучал курсы, выходящие далеко за рамки моего этапа обучения, и выиграл множество медалей на математических соревнованиях. А после поступления в университет я был совершенно уверен в том, что участники математической олимпиады станут величайшими математиками моего поколения. Однако на самом деле все сложилось не совсем так. Из этой группы молодых звезд вышло много превосходных математиков, таких как Терри Тао – специалист по гармоническому анализу, получивший медаль Филдса. Однако большинство математиков, с которыми я сейчас работаю, не были членами математических кружков в тринадцатилетнем возрасте; их способности и таланты сформировались в разные периоды жизни. Так стоит ли бросать занятия математикой в средней школе?
Когда довольно много времени работаешь в математике (а я считаю, что этот урок применим и в других областях), то начинаешь понимать, что всегда есть тот, кто в чем-то тебя превосходит. Люди просто начинают смотреть на того, кто доказал хорошие теоремы; тот, кто доказал хорошие теоремы, смотрит на того, кто доказал много хороших теорем; тот, кто доказал много хороших теорем, смотрит на того, кто получил Филдсовскую премию; обладатели медали Филдса следят за теми, кто входит во «внутренний круг» медалистов, а члены этого круга всегда могут обратить свой взор на тех, кого уже с нами нет. Никто никогда не смотрит в зеркало и не говорит: «Надо признать, я лучше Гаусса». Тем не менее за последнюю сотню лет эти «болваны по сравнению с Гауссом» совместными усилиями обеспечили величайший расцвет математического знания, который когда-либо видел мир.
Математика – это по большей части коллективная область деятельности, в которой каждое открытие является продуктом огромной сети умов, работающих над достижением общей цели, даже если мы приписываем честь этого открытия человеку, который закладывает последний камень в здание этих трудов. Очень хорошо сказал об этом Марк Твен: «Требуется тысяча человек, чтобы изобрести телеграф или паровой двигатель, или фонограф, или телефон, или еще что-нибудь столь же важное, а мы приписываем изобретение последнему из них и забываем об остальных».
Это напоминает американский футбол. Безусловно, существуют моменты, когда один игрок берет под свой контроль всю игру, и эти моменты мы запоминаем, отдаем им должное и впоследствии еще долго вспоминаем. Однако такие моменты не являются нормальным режимом игры в футбол, и не благодаря им команды одерживают победы в большинстве матчей. Когда квотербек делает быстро двигающемуся ресиверу блестящий пас, завершающийся тачдауном, вы видите согласованные действия многих людей – не только квотербека и ресивера, но и лайнменов нападения, которые сдерживали атаку защитников довольно долго, чтобы квотербек подготовился и бросил мяч, а это в свою очередь стало возможным благодаря ранинбеку, который в самый критический момент отвлек внимание защитников. Кроме того, есть еще и координатор нападения, который задал тон игры, а также его помощники с планшетами в руках, и тренеры, которые поддерживают игроков в хорошем состоянии, для того чтобы они могли бегать и бросать мяч… Никто не называет всех этих людей гениями. Но они создают условия, при которых гений может реализовать себя.
Терри Тао пишет:
Популярный образ одинокого (и, может, немного сумасшедшего) гения, который игнорирует литературу и другие источники устоявшихся представлений и которому благодаря какому-то непостижимому вдохновению (возможно, усиленному мягким всплеском страдания) удается найти поразительно оригинальное решение задачи, поставившей в тупик всех специалистов, – это очаровательный и романтический образ, но абсолютно неправильный, во всяком случае в мире современной математики. Безусловно, в этой области действительно есть впечатляющие, глубокие и удивительные результаты и озарения, но они достаются тяжелым трудом и являются результатом многих лет, десятилетий или даже столетий упорной работы и успехов многих хороших и великих математиков. Переход от одного уровня понимания к следующему может быть в высшей степени нетривиальным и порой довольно неожиданным, но все же он опирается на фундамент предшествующей работы, а не начинается с чистого листа… На самом деле я считаю, что современные реалии математических исследований (когда прогресс достигается естественным образом, как следствие упорного труда, в основе которого лежит интуиция, литература и немного удачи) приносят гораздо большее удовлетворение, чем мои прежние романтические представления о математике как о науке, развивающейся в основном благодаря мистическому вдохновению некой редкой породы «гениев».
Я не утверждаю, что было бы неправильным называть Гильберта гением. Однако правильнее говорить, что гениально то, чего достиг Гильберт. Гениален не человек, гениально то, что он делает.
Политическая логика
Политическая логика – это не формальная система в том смысле, который подразумевали Гильберт и другие специалисты по математической логике, но математики с формалистским мировоззрением не могли не подходить к политике с такими же методологическими предпочтениями. К этому их призывал сам Гильберт, который в своей лекции Axiomatic Thought («Аксиоматическое мышление»), прочитанной в 1918 году, отстаивал идею о том, что другие науки также должны взять на вооружение аксиоматический подход, оказавшийся столь успешным в математике.
Например, Гёдель, теорема которого исключила возможность окончательного изгнания противоречий из арифметики, был также обеспокоен Конституцией США, которую он изучал во время подготовки к экзамену на получение американского гражданства в 1948 году. Он считал, что этот документ содержит противоречие, которое может помочь фашистской диктатуре взять страну под свой контроль абсолютно конституционным путем. Друзья Гёделя Альберт Эйнштейн и Оскар Моргенштерн умоляли его избегать этой темы на экзамене, но, как вспоминает об этом Моргенштерн, беседа закончилась так:
Экзаменатор. Итак, мистер Гёдель, откуда вы?Гёдель. Откуда я? Из Австрии.Экзаменатор. Какая власть действует у вас в Австрии?Гёдель. Это была республика, но конституция была такой, что в итоге она превратилась в диктатуру.Экзаменатор. О! Это очень плохо! В нашей стране такое невозможно.Гёдель. Возможно, и я могу это доказать.
К счастью, экзаменатор поспешно сменил тему, и гражданство было предоставлено Гёделю надлежащим образом. Что касается характера противоречий, которые Гёдель обнаружил в Конституции США, скорее всего информация о них утрачена для истории математики. Может, это и к лучшему!
Приверженность Гильберта логическому принципу и дедукции часто приводила к тому, что он, подобно Кондорсе, часто придерживался на удивление современных взглядов по вопросам, не имеющим отношения к математике. Не без определенных политических последствий для себя он отказался подписать опубликованное в 1914 году «Обращение к культурному миру», которое оправдывало войну кайзера в Европе посредством длинного списка опровержений, начинавшихся со слов «Это неправда, что…»: «Это неправда, что Германия нарушила нейтралитет Бельгии» и так далее. Обращение подписали многие великие немецкие ученые, такие как Феликс Клейн, Вильгельм Рентген и Макс Планк. Гильберт, не имея уверенности, что все эти утверждения соответствуют истине, отказался поставить свою подпись.
Год спустя, когда профессорско-преподавательский состав Гёттингенского университета отказался предложить должность великому алгебраисту Эмми Нётер, утверждая, что студентам нельзя будет предложить изучать математику у женщины, Гильберт отреагировал на это так: «Не понимаю, как пол кандидата может служить доводом ее назначения. Ведь здесь университет, а не баня».
Однако логический анализ политики имеет свои пределы. В 1930-е годы Гильберт был уже пожилым человеком и, по всей вероятности, утратил способность понимать, что происходило в его родной стране после прихода нацистов к власти. Отто Блюменталь, первый ученик Гёделя, получивший докторскую степень, посетил его в Гёттингене в 1938 году, чтобы поздравить с семидесятивосьмилетием. Блюменталь был христианином, но родился в еврейской семье, и по этой причине его уволили с академической должности в Ахене. (В том же году Абрахам Вальд уехал из оккупированной немцами Австрии в Соединенные Штаты.)
В своей книге о Гильберте Констанс Рид вспоминает разговор на приеме в честь дня рождения математика:
– Какие предметы вы читаете в этом семестре? – спросил Гильберт.
– Я больше не читаю лекций, – осторожно напомнил ему Блюменталь.
– Что значит, что вы не читаете лекций?
– Мне больше не разрешают их читать.
– Но это совершенно невозможно! Этого не может быть. Никто не имеет права смещать профессора до тех пор, пока он не совершил какое-либо преступление. Почему вы не обращаетесь в суд?
Прогресс человеческого разума
Кондорсе также упорно держался за свои формалистские представления о политике, даже когда они не совсем соответствовали реальности. Существование циклов Кондорсе означало, что любая избирательная система, подчиняющаяся его базовой, на первый взгляд неоспоримой аксиоме (если большинство избирателей отдают предпочтение кандидату А перед кандидатом Б, Б не может быть победителем), может стать жертвой внутреннего противоречия. Кондорсе потратил большую часть последнего десятилетия своей жизни на попытки решить проблему циклов, разрабатывая все более сложные системы голосования, которые должны были исключить проблему противоречивости коллективного мнения. Однако ему так и не удалось добиться успеха.
Как правило, мы не можем избежать принятия решений такого рода, которые можно было бы назвать неоднозначными, иначе как требуя значительного большинства голосов или позволяя голосовать только людям просвещенным… Если мы не сможем найти достаточно просвещенных избирателей, мы должны избегать плохого выбора, принимая в качестве кандидатов только тех людей, компетентности которых мы можем доверять.
Однако проблема была не в избирателях, а математике. Сейчас мы понимаем, что Кондорсе с самого начала был обречен на неудачу. Экономист Кеннет Эрроу доказал в своей докторской диссертации 1951 года, что даже гораздо более слабая совокупность аксиом, чем аксиомы Кондорсе, – совокупность требований, которые на первый взгляд так же трудно поставить под сомнение, как и правила арифметики Пеано, также влечет за собой парадоксы. Это была невероятно элегантная работа, которая помогла Эрроу получить Нобелевскую премию по экономике за 1971 год, но она, безусловно, огорчила бы Кондорсе точно так же, как огорчила Гильберта теорема Гёделя.
А может, и не огорчила бы: Кондорсе был человеком, которого было трудно чем-то расстроить. Когда Французская революция набрала обороты, его мягкие принципы республиканской формы правления быстро вытеснили более радикальные якобинцы. Кондорсе впервые попал в политическую изоляцию, а затем был вынужден скрываться, чтобы избежать гильотины. Тем не менее его не покинула вера в неотвратимость прогресса под влиянием здравого смысла и математики. Уединившись в надежном доме в Париже, зная, что у него, возможно, осталось не так уж много времени, Кондорсе написал труд «Esquisse d’un tableau historique des progrèts de l’esprit humain» («Эскиз исторической картины прогресса человеческого разума»), в котором изложил свое видение будущего. Это удивительно оптимистичный документ, описывающий мир, в котором такие проблемы, как роялизм, предубеждения в отношении пола, голод и старость, будут решены в свое время посредством науки. Вот типичный отрывок из этой работы:
Должен ли человеческий род улучшаться или благодаря новым открытиям в науках и искусствах и, в силу необходимого следствия, – в средствах создания частного благосостояния и общего благополучия, или благодаря развитию моральных принципов поведения, или, наконец, в силу действительного совершенства интеллектуальных, моральных и физических способностей, которое может быть обусловлено или совершенством инструментов, увеличивающих интенсивность и направляющих употребление этих способностей, или даже совершенством естественной организации человека?
В наше время работа Кондорсе «Эскиз» известна опосредованно: она вдохновила Томаса Мальтуса, считавшего предсказания Кондорсе безнадежно оптимистичными, на написание намного более знаменитой, но и более мрачной книги о будущем человечества.
Вскоре после того, как был написан приведенный выше отрывок, в марте 1794 года (или, согласно рационализированному революционному календарю, в жерминале второго года) Кондорсе поймали и арестовали. Через два дня его нашли мертвым; одни говорят, что он совершил самоубийство, другие – что его убили.
Подобно тому как модель математики Гильберта уцелела, несмотря на разрушение его формальной программы Гёделем, подход Кондорсе к политике также пережил его гибель. Мы больше не рассчитываем на то, что нам удастся найти системы голосования, удовлетворяющие его аксиоме. Однако мы стали приверженцами более фундаментальной убежденности Кондорсе в том, что численная «социальная математика» (то, что мы называем сейчас социологией) должна играть свою роль в определении надлежащего поведения правительства. Это и были те «инструменты, увеличивающие интенсивность и направляющие употребление [наших] способностей», о которых с таким воодушевлением писал Кондорсе в «Эскизе».
Идеи Кондорсе настолько переплетены с современным подходом к политике, что мы вряд ли воспринимаем их как выбор. Однако это и есть выбор. И я считаю, что это правильный выбор.

