Рассмотрим аукцион второй цены, на котором один товар разыгрывается между n участниками. Обозначим v_i истинную ценность товара для участника i (от английского слова value – ценность). Далее обозначим через b_i ставку участника i (от англ. bid – ставка). Эти обозначения будем использовать для любого i = 1,2, …, n.

Совместимость по стимулам означает, что верна следующая теорема.

Теорема (Викри). Участник i получает максимальную прибыль, если b_i = v_i.

Доказательство. Если участник i получает товар, следовательно, его ставка b_i была самой высокой. Поскольку мы имеем дело с аукционом второй цены, то стоимость товара равна самой высокой из оставшихся ставок:

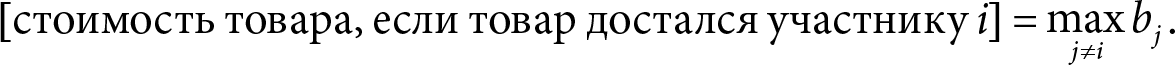
При этом ценность товара для участника i равна v_i. Значит, если участник i получает товар, то его прибыль составит

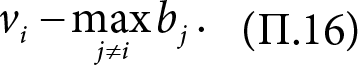
Если участник i товар не получает, он не приобретает никакой ценности и ничего не платит, то есть его прибыль равна нулю.

Дальше доказательство ведется так же, как в разделе в главе 8, и в качестве иллюстрации мы можем по-прежнему использовать и . Допустим, что ставки всех участников, кроме i, фиксированы. Мы покажем, что при правдивой ставке b_i = v_i прибыль участника i та же или больше, чем при повышенной ставке b_i > v_i или пониженной b_i < v_i. Подчеркнем, что это утверждение верно при любых (фиксированных) ставках других участников.

Предположим, что b_i > v_i. Рассмотрим три случая относительно ставок b_j, j≠i.

1. Допустим, что b_i – самая высокая ставка и, кроме того, все остальные участники поставили меньше, чем v_i ( вверху). Тогда товар по-прежнему достается участнику i по стоимости max_j≠ib_j, и участник i получает точно такую же прибыль (П.16), что и при правдивой ставке v_i.

2. Теперь предположим, что другой участник k сделал ставку b_k > b_i (см. в середине). Тогда участник i товар не получает, его прибыль равна нулю. Но поскольку b_i > v_i, то и при честной ставке v_i участник i тоже не получил бы товар. Значит, в этом случае прибыль участника i при честной ставке тоже равна нулю.

3. Наконец, допустим, что b_i – самая высокая ставка и v_i < max_j≠ib_j < b_i (см. внизу). Так как v_i < b_i, такая ситуация возможна. Она возникает, когда самая высокая ставка других участников выше v_i, но ниже b_i. Если бы i поставил v_i, то i не получил бы товар, прибыль была бы равна нулю. Но теперь b_i – самая высокая ставка, поэтому товар достается i. Прибыль i по-прежнему вычисляется по формуле (П.16), но только прибыль становится отрицательной, поскольку ценность товара меньше его стоимости. Значит, в этом случае прибыль i меньше, чем при честной ставке.

Во всех трех случаях 1–3 участник i не получил прибыль выше, чем при честной ставке v_i.

Теперь предположим, что b_i < v_i, то есть ставка занижает реальную ценность. Опять рассмотрим три случая относительно ставок других участников b_j, j≠i.

1ʹ. Допустим, b_i – самая высокая ставка ( вверху). Тогда товар по-прежнему достается участнику i по стоимости max_j≠ib_j. В этом случае прибыль участника i та же, что и прежде (П.16). Она в точности такая же, как и при честной ставке v_i.

2ʹ. Теперь предположим, что другой участник l сделал ставку b_l > v_i (рис. 8.3 в середине). В этом случае при честной ставке v_i участник i товар не получает.

Но тогда и при заниженной ставке b_i < v_i участник i не получит товар. Значит, прибыль i равна нулю и при честной, и при заниженной ставке.

3ʹ. Наконец, допустим, что b_i < max_j≠ib_j < v_i ( внизу). Так как b_i < v_i такая ситуация возможна. Она возникает, когда самая высокая ставка других участников выше b_i, но ниже v_i. Тогда при честной ставке товар достался бы участнику i, и его прибыль, по формуле (П.16), была бы положительной. Но поскольку b_i теперь не самая высокая ставка, товар достанется другому участнику и прибыль участника i равна нулю. Значит, в этом случае прибыль i меньше, чем при честной ставке.

Во всех трех случаях 1ʹ–3ʹ участник i не получил более высокую прибыль, чем при честной ставке v_i.

В результате делаем вывод, что и при заниженной, и при завышенной ставке участник i получает не больше, чем при честной ставке b_i = v_i. Таким образом, мы доказали, что в аукционе второй цены выгоднее всего делать честную ставку.