Те или иные математические методы применялись в шифровании уже давно. Тем не менее, когда задача становится по-настоящему масштабной, возникает потребность в системном подходе. Если раньше задача решалась по-разному в каждом отдельном случае, то теперь появляется теория, из которой следует не один, а целый класс методов. Эта теория начинает широко опираться на другие теории, результаты осмысливаются, фильтруются и уже в стройном виде вливаются в практику и попадают в университетские учебники.

В наше время криптография – это устоявшаяся наука. На языке, принятом в ней, задача шифрования звучит так. Есть два человека – Алиса и Боб (А и В), – которые желают передавать друг другу сообщения, но при этом не хотят, чтобы злонравная Ева (Е от английского слова eavesdropping – подслушивание), перехватившая их, смогла прочесть, о чем в них идет речь.

Чтобы было легче понять научный подход к проблеме, давайте шифровать цифры вместо букв. В конце концов, мы всегда можем заменить буквы на числа (хотя бы 1, 2, … 33). Разумеется, математикам так удобнее.

Что такое шифр? Это превращение одного числа в другое. На входе мы вводим число х, а на выходе получаем число у. Число у – это преобразование числа х. В математике это записывается известным со школы обозначением

y = f (x).

Возьмем тот же простой пример, когда буква заменяется следующей по алфавиту. Аналогично Алиса и Боб могут договориться о замене целого числа следующим по порядку: вместо 1 писать 2, вместо 2 – 3 и так далее. Тогда для произвольного числа х наш процесс шифрования будет выглядеть как на рис. 6.1 сверху.

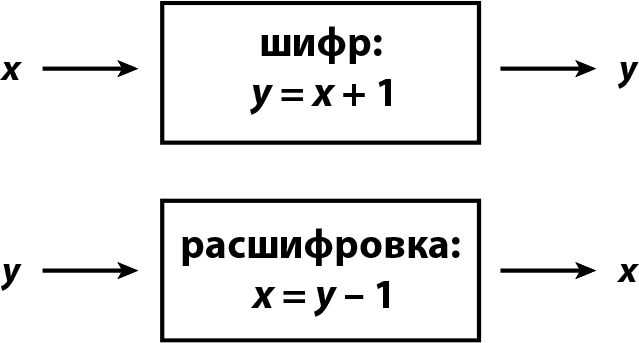
Рис. 6.1. Элементарная шифровка и расшифровка. В данном случае y = f(x) = x + 1

Теперь представим, что Ева умна и хитра и в принципе в состоянии перехватить или вычислить секретный ключ (в данном случае ключ – это договоренность, что Алиса и Боб пишут x + 1 вместо х). Тогда ей ничего не стоит расшифровать сообщение, она должна всего лишь вычесть единицу!

Понятно, что столь элементарный шифр нас не устраивает. Если Алиса хочет защитить свои сообщения от Евы, то в идеале ей нужен такой шифр, который зашифровать было бы просто, а расшифровать трудно. О том, как будет расшифровывать Боб, мы расскажем ниже. Пока, в терминах математики, нам следует найти очень особенное преобразование f, удовлетворяющее вот такому довольно странному условию: если мы знаем х и знаем f, мы легко можем вычислить y = f(x), а вот если мы знаем у и знаем f, то вычислить х все равно очень сложно.

Схематически наше пожелание выглядит как на рис. 6.2. И сразу возникает закономерный вопрос: а существуют ли в природе подобные преобразования?

Рис. 6.2. Шифр y = f (x), который сложно расшифровать, даже зная преобразование f

Если задуматься, станет ясно, что придумать подходящую функцию f и главное доказать, что она обладает нужными свойствами, вовсе не легко! Почему «главное – доказать»? Совсем не потому, что математики так уж любят доказательства. А потому, что тогда мы точно будем знать, что хитроумная Ева не сможет взломать шифр. Против математических доказательств Ева бессильна.

Оказывается, такие преобразования f есть. Более того, можно сделать так, чтобы Боб и Алиса могли расшифровывать сообщения, а Ева – нет! Пока не доказано, что задача расшифровки абсолютно безнадежна. Но известно, что она относится к определенной категории трудных задач, эффективное решение которых еще не найдено. Именно эти шифры используются для обмена секретными ключами, чтобы установить безопасную связь через интернет. Для построения таких шифров требуется глубокая математика. В данном случае – теория чисел.