Правила дифференцирования

Книга: Магия математики: Как найти x и зачем это нужно

Чем больше функций мы продифференцируем, тем больше задач сможем решить. Пожалуй, самой важной функцией в исчислении является показательная функция y = e^x. Ее особенность в том, что она равна собственной производной.

Теорема: Если y = e^x, то y' = e^x.

Отступление
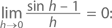
Почему f(x) = e^x соответствует f'(x) = e^x? Смотрите, в чем секрет. Сначала обратите внимание на то, что

Вспомним, что е, по сути, есть

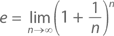
что означает, что с увеличением n значение члена (1 + 1/n)ⁿ будет все ближе и ближе подходить к e. Теперь предположим, что h = 1/n. При очень большом значении n h = 1/n находится очень близко к 0. Следовательно, при h, близком к 0,

e ≈ (1 + h)1/h
Возведя обе части в степень h (и помня, что (a^b)^c = a^bc), получаем

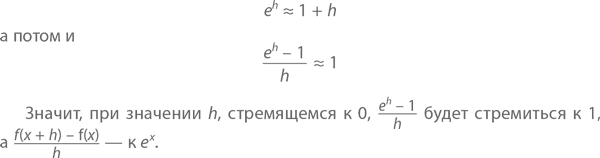
А есть ли еще такие функции, которые равны своим производным? Есть. Но все они сводятся к y = ce^x, где c заменяется любым действительным числом (в том числе и 0, который превращает функцию в постоянную y = 0).

Не так давно мы выяснили, что при сложении функций производная суммы равна сумме производных. А что насчет умножения? Увы, но производная произведения не равна произведению производных. Тем не менее посчитать ее не очень сложно – для этого достаточно воспользоваться несложной теоремой.

Теорема (правило дифференцирования произведения функций): Если y = f(x)g(x), то

y' = f(x)g'(x) + f'(x)g(x)

Например, согласно правилу дифференцирования произведения, чтобы продифференцировать y = x³e^x, нам нужно взять f(x) = x³ и g(x) = ex. В результате у нас получится

y' = f(x)g'(x) + f'(x)g(x) = x³e^x + 3x²e^x

Обратите внимание, что при f(x) = x³ и g(x) = x⁵ их произведение, согласно тому же правилу, составит x³x⁵ = x⁸. Производная же будет выглядеть как

y' = x³(5x⁴) + 3x²(x⁵) = 5x⁷ + 3x⁷ = 8x⁷

что полностью соответствует правилу дифференцирования степенной функции.

Отступление
Доказательство (правило дифференцирования произведения функций): Предположим, что u(x) = f(x)g(x). Тогда

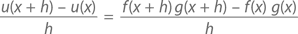
А дальше творим истинно математическое волшебство – добавляем к числителю 0, но не привычным способом, а с помощью прибавления и вычитания f(x + h)g(x):

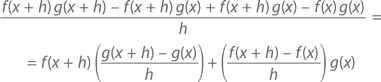
Так как h → 0, в результате имеем f(x)g'(x) + f'(x)g(x), что и требовалось доказать.◻

Но доказанное правило полезно не только в этом конкретном случае – с его помощью можно найти производные других функций. Мы уже доказали, что правило дифференцирования степенной функции верно при положительных значениях показателя степени. Давайте посмотрим, как оно поведет себя при дробных и отрицательных значениях.

Например, согласно правилу дифференцирования степенной функции

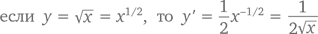
Сможем ли мы доказать его с помощью правила дифференцирования произведения? Предположим u(x) = √x. Тогда

u(x) u(x) = √x √x = x

Продифференцировав обе стороны и применив правило дифференцирования произведения, получаем

u(x) u'(x) + u'(x) u(x) = 1

Следовательно,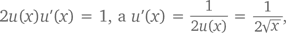

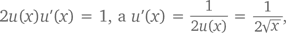как мы и предполагали.

Отступление
Правило дифференцирования произведения при отрицательных значениях степени гласит, что y = x⁻ⁿ будет иметь производную Чтобы это доказать, возьмем u(x) = x⁻ⁿ, где n ≥ 1. Согласно определению, при x ≠ 0

u(x)xn = x^–ⁿxⁿ = x0 = 1
Продифференцировав обе стороны и применив правило дифференцирования произведения, получаем

u(x)(nxⁿ⁻¹) + u'(x)xⁿ = 0
Разделив всех члены уравнения на xⁿ и перенеся первый член в другую часть уравнения, получаем

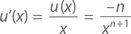
что и требовалось доказать.◻

Следовательно, если y = 1/x = x^–1, то y' = −1/x², если y = 1/x² = x^–2, то y' = −2x^–3 = −2/x³, и т. д.

Помните, в 7 главе мы искали такое положительное значение x, при котором функция

y = x + 1/x

показала бы минимальное значение? Тогда мы нашли решение с помощью геометрии, показав, что результат может быть достигнут при x = 1. Но можно решить эту задачу значительно проще: это значит, что y' = 0, это дает нам 1 – 1/x² = 0, а единственная положительная величина, которая удовлетворяет этому условию, – x = 1.

Что касается тригонометрических функций, то их дифференцировать ничуть не сложнее. Обратите внимание, что для доказательства следующей теоремы нам нужно, чтобы углы были выражены в радианах.

Теорема: Если y = sin x, то y' = cos x, а если y = cos x, то y' = –sin x. Другими словами, производная синуса равна косинусу, а производная косинуса – синусу со знаком минус.

Отступление
Доказательство: Для доказательства нам потребуется следующая лемма (лемма – это подсобная, подготовительная теорема, с помощью которой можно доказать более сложное и серьезное утверждение).

Лемма:

Здесь утверждается, что значение любого угла h, равного чуть больше, чем 0 (в радианах), будет близко к значению h, в то время как значение косинуса будет близко к 1. С помощью калькулятора, например, можно выяснить, что sin 0,0123 = 0,0122996…, а cos 0,0123 = 0,9999243…. С помощью этой леммы можно продифференцировать любой синус или косинус. Тождество sin (A + B) из главы 9 говорит нам, что

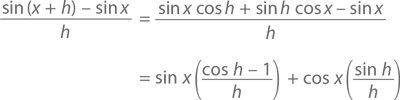
А так как h → 0, то, согласно нашей лемме, это уравнение превращается в (sin x)(0) + (cos x)(1) = cos x. Подобным же образом

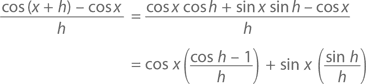
И снова h → 0 дает нам (cos x)(0) – (sin x)(1) = –sin x, что и требовалось доказать.◻

Отступление
То, что можно доказать с помощью такого вот графика:

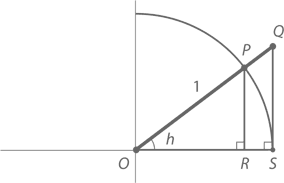
На единичной окружности, часть которой изображена выше, R = (1, 0), а P = (cos h, sin h), где h есть небольшой угол с положительным значением. В прямоугольном треугольнике OQR

Рассмотрим сектор OPR, имеющий клинообразную форму. Площадь единичной окружности равна π1² = π, сектор OPS – ее часть, выражаемая дробью h/(2π). Следовательно, площадь сектора OPR составляет π(h/2π) = h/2.

Так как сектор OPR содержит в себе треугольник OPS, а тот, в свою очередь, – треугольник OQR, сравнение их площадей дает нам

Для положительных значений a, b и c, если a < b < c, то 1/c < 1/b < 1/a. Следовательно,

А так как h → 0, и cos h, и 1/cos h будут стремиться к 1, что и требовалось доказать.

◻

Отступление
С помощью полученного результата и нескольких алгебраических формул (включая cos² h + sin² h = 1) можно доказать, что

◻

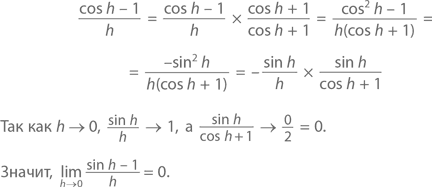
Производные синуса и косинуса – ключи к дифференцированию тангенса.

Теорема: Если y = tan x, то y' = 1/(cos²x) = sec²x.

Доказательство: Предположим, что u(x) = tan x = (sin x)/(cos x). Тогда

tan (x) cos x = sin x

Продифференцировав обе части и применив правило дифференцирования произведения функций, получим

tan x (–sin x) + tan' (x) cos x = cos x

Разделим все члены на cos x и решим уравнение для tan' (x):

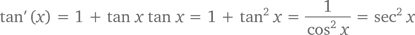
в котором предпоследнее значение получается в результате деления тождества cos 2x + sin 2x = 1 на cos 2x.

Отступление
Доказательство правила дифференцирования частного: Так как u(x)g(x) = f(x), продифференцировав обе части уравнения, в соответствии с правилом дифференцирования произведения получим

u(x) g'(x) + u'(x) g(x) = f'(x)
Умножив все на g(x), получим

g(x) u(x) g'(x) + u'(x) g(x) g(x) = g(x) f'(x)
Заменим g(x) u(x) на f(x) и решим уравнение для u'(x), что приведет нас к искомому результату.◻

Теперь мы умеем дифференцировать многочлены, показательные и тригонометрические функции. Также мы научились дифференцировать их суммы, произведения и частные. Но есть еще сложные функции – функции от функций, с которыми тоже нужно уметь обращаться. Правило дифференцирования сложной функции иначе называют цепным правилом. Согласно ему, например, если f(x) = sin x, а g(x) = x³, то

f(g(x)) = sin(g(x)) = sin(x³)

Не перепутайте: это не то же самое, что

g(f(x)) = g(sin x) = (sin x)³

Теорема (цепное правило): Если y = f(g(x)), то y' = f'(g(x))g'(x).

Например, если f(x) = sin x, а g(x) = x³, то f'(x) = cos x, а g'(x) = 3x². Согласно цепному правилу, при y = f(g(x)) = sin (x³)

y' = f'(g(x))g'(x) = cos(g(x))g'(x) = 3x² cos(x³)

Обобщая, можно сказать, что при y = sin (g(x)) y' = g'(x) cos(g(x)). Та же логика подсказывает нам, что y = cos (g(x)) имеет производную y' = –g'(x) sin (g(x)).

С другой стороны, функция y' = –g'(x) sin (g(x)), согласно цепному правилу, выглядит так:

y' = g'(f(x))f'(x) = 3(f(x)²)f'(x) = 3 sin² x cos x

Обобщим и это: цепное правило говорит нам, что при y = (g(x))ⁿ y' = n(g(x))^n–1g'(x). А что насчет y = (x³)⁵?

y' = 5(x³)⁴(3x²) = 5x¹²(3x²) = 15x¹⁴

что полностью соответствует правилу дифференцирования произведения функций.

Продифференцируем y = √(x2 + 1) = (x² +1)^½.

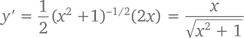
Со степенными функциями дело обстоит ничуть не сложнее. Так как ex является собственной производной, то при y = e^g^(x) имеем

y' = g'(x)eg(x)

Например, производная y = e^x³ – y' = (3x²)e^x³.

Обратите внимание, что функция y = e^kx имеет производную y' = ke^kx = ky. Это одна из причин, почему показательные (экспоненциальные) функции так важны – они появляются, когда скорость роста функции пропорциональна величине ее значения. По этой причине показательные функции часто связаны с процессами в финансовой сфере и в биологии.

Натуральный логарифм ln x обладает одним интересным свойством:

e^{ln x} = x

при любом значении x, большем 0. Чтобы найти его, логарифма, производную, воспользуемся цепным правилом. Допустив, что u(x) = ln x, получим e^u^(x) = x. Продифференцировав обе части этого уравнения, получаем u'(x)e^u^(x) = 1. Но поскольку e^u(x) = x, u'(x) = 1/x. Другими словами, если y = ln x, тогда y' = 1/x. Вновь применив цепное правило, получаем: если y = ln (g(x)), то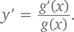

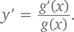
Давайте соберем все найденное с помощью цепного правила в таблицу:

Хотите применить все это на практике? Вот вам задачка, практичней некуда. Корова Клара пасется в километре на север от реки (оси x), в 3 километрах на запад и в километре на юг от коровника. Наевшись и нагулявшись, она решила попить водички и пойти домой. Естественно, ей хочется сделать это все как можно быстрее. Где именно ей нужно спуститься к реке, чтобы максимально сократить путь?

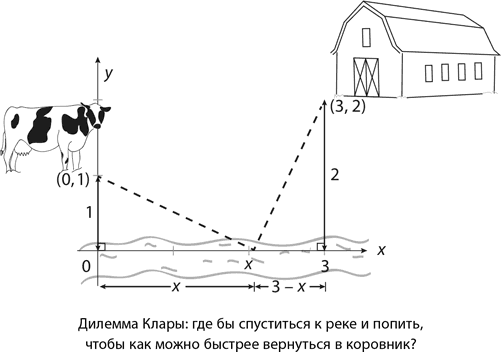
Предположим, что корова решила двинуться с луга (то есть из стартовой точки (0, 1)) к месту водопоя (то есть к точке (x, 0)) напрямик. Согласно теореме Пифагора (или формуле расстояния), длина ее маршрута до реки составит √(x² + 1), а до амбара, находящегося в точке B = (3, 2), – √((3 – x)² + 4) = √(x² – 6x + 13). Значит, задача сводится к нахождению такого значения x в диапазоне от 0 до 3, при котором достигается минимальное значение функции

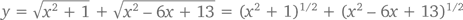
Продифференцировав это уравнение (с помощью цепного правила) и приравняв его к 0, получим

Проверить это можно, взяв x = 1, тогда левая часть уравнения превращается в 1/√2 – 2/√8, что и в самом деле равно 0 (а можно добавить x/√(x² + 1) справа, возвести обе части в квадрат и умножить члены крест-накрест – после нескольких сокращений вы придете к x = 1).

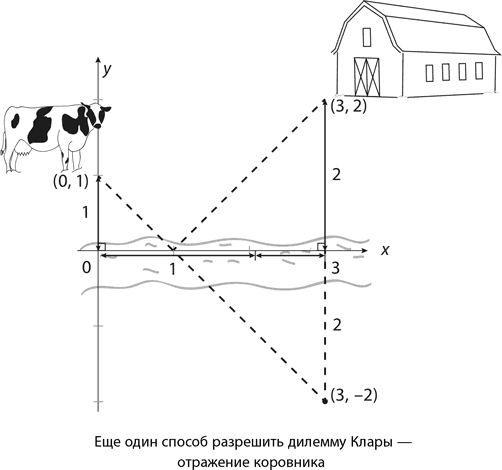
Неплохим вариантом будет метод отражения, уже знакомый нам по главе 7. Представьте, что вместо коровника (точка B = (3, 2)) корова пошла к его отражению (точка B' = (3,–2)), как показано на следующем рисунке.

Расстояние до B' абсолютно такое же, как и до B. Любой отрезок, соединяющий точку, расположенную на севере от реки, с ее «отражением», расположенным к югу от реки, неизбежно пересечет ось x. Кратчайшим маршрутом в этом случае будет прямая линия от (0, 1) до (3, –2) (с наклоном –3/3 = –1), пересекающая ось x при x = 1. И никаких квадратных корней!

Назад: Максимум против минимума

Дальше: Фокус-покус: ряд Тейлора