Книга: Магия математики: Как найти x и зачем это нужно
Назад: Правило суммы и произведения
Дальше: Закономерности треугольника Паскаля
Лотерея и покер
В этом разделе мы используем то, что только что узнали, для подсчета своих шансов выиграть в лотерею или собрать нужную комбинацию в покере. Но позвольте сначала предложить вам немного мороженого.
Допустим, вам предлагают наполнить рожок 3 шариками разных сортов мороженого. Всего можно выбирать из 10 сортов. Сколько всего можно получить разных рожков? Не забудьте: порядок шариков разных сортов имеет значение (а как же иначе? Ведь вкус-то разный!). Если повторяться можно, получается, что у нас есть 10 вариантов для каждого из трех шариков: 103 = 1000 вероятных комбинаций. Ну а если нельзя – их количество сокращается до 10 × 9 × 8 = 720, как показано на картинке чуть ниже.
Теперь кое-что поинтереснее. Как будут лежать три шарика трех разных сортов в вазочке, если их порядок не важен? Можно сказать точно: их будет меньше. А конкретно – в 6 раз меньше. Попытаемся понять, почему. Лежащие в вазочке 3 шарика мороженого 3 разных сортов (допустим, шоколадное, ванильное и мятное) можно переложить в рожок 3! = 6 способами. Значит, из 1 варианта вазочки можно собрать 6 вариантов рожков. Количество вазочек, таким образом, будет равняться
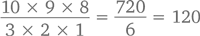
Другой способ представить 10 × 9 × 8 – 10!/7! (хотя первый пример, конечно, легче подсчитать). Значит, количество чашек – 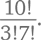 Такая запись читается как «число сочетаний из 10 по 3», обозначается символом
Такая запись читается как «число сочетаний из 10 по 3», обозначается символом 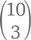 и равняется 120. Другими словами, число вариантов при выборе определенного количества различных объектов, равного n, из общего количества различных объектов, равного k (в произвольном порядке), называется «числом сочетаний из n по k» и подсчитывается по формуле
и равняется 120. Другими словами, число вариантов при выборе определенного количества различных объектов, равного n, из общего количества различных объектов, равного k (в произвольном порядке), называется «числом сочетаний из n по k» и подсчитывается по формуле
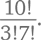 Такая запись читается как «число сочетаний из 10 по 3», обозначается символом
Такая запись читается как «число сочетаний из 10 по 3», обозначается символом 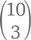 и равняется 120. Другими словами, число вариантов при выборе определенного количества различных объектов, равного n, из общего количества различных объектов, равного k (в произвольном порядке), называется «числом сочетаний из n по k» и подсчитывается по формуле
и равняется 120. Другими словами, число вариантов при выборе определенного количества различных объектов, равного n, из общего количества различных объектов, равного k (в произвольном порядке), называется «числом сочетаний из n по k» и подсчитывается по формуле

Математики называют такого рода вычисления сочетаниями или комбинациями, а числа вида 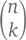 – биноминальными коэффициентами. Вычисления же при строго определенном порядке объектов называется перестановкой или пермутацией. Эти два понятия часто путают: например, мы привыкли думать, что на «кодовом» замке нужно подбирать «комбинации» цифр, хотя по сути это не комбинации, а перестановки, ведь порядок чисел, составляющих код, имеет большое, если не решающее, значение.
– биноминальными коэффициентами. Вычисления же при строго определенном порядке объектов называется перестановкой или пермутацией. Эти два понятия часто путают: например, мы привыкли думать, что на «кодовом» замке нужно подбирать «комбинации» цифр, хотя по сути это не комбинации, а перестановки, ведь порядок чисел, составляющих код, имеет большое, если не решающее, значение.
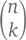 – биноминальными коэффициентами. Вычисления же при строго определенном порядке объектов называется перестановкой или пермутацией. Эти два понятия часто путают: например, мы привыкли думать, что на «кодовом» замке нужно подбирать «комбинации» цифр, хотя по сути это не комбинации, а перестановки, ведь порядок чисел, составляющих код, имеет большое, если не решающее, значение.
– биноминальными коэффициентами. Вычисления же при строго определенном порядке объектов называется перестановкой или пермутацией. Эти два понятия часто путают: например, мы привыкли думать, что на «кодовом» замке нужно подбирать «комбинации» цифр, хотя по сути это не комбинации, а перестановки, ведь порядок чисел, составляющих код, имеет большое, если не решающее, значение.

Если ваш продавец мороженого предлагает 20 разных сортов, то, направляясь туда с намерением купить 5 разных шариков (в случайном порядке), вам придется выбирать из
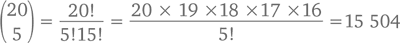
вариантов. Кстати, если на вашем калькуляторе не предусмотрено специальной кнопки, чтобы подсчитать  просто наберите в любом поисковике «число сочетаний из 20 по 5», и вы увидите веб-калькулятор с готовым ответом.
просто наберите в любом поисковике «число сочетаний из 20 по 5», и вы увидите веб-калькулятор с готовым ответом.
 просто наберите в любом поисковике «число сочетаний из 20 по 5», и вы увидите веб-калькулятор с готовым ответом.
просто наберите в любом поисковике «число сочетаний из 20 по 5», и вы увидите веб-калькулятор с готовым ответом.Биноминальные коэффициенты, впрочем, могут появляться и там, где порядок расположения объектов определенную роль все же играет. Если вы 10 раз подбросите монетку, сколько всего у вас будет возможных последовательностей результатов (вроде О-Р-О-Р-Р-О-О-Р-Р-Р или О-О-О-О-О-О-О-О-О-О)? Так как каждый бросок имеет два возможных исхода, правило произведения говорит нам, что их будет 210 = 1024, причем шансы выпадения каждой стороны абсолютно равны. (Некоторые, конечно, удивятся: вероятность того, что выпадет вторая комбинация, вроде бы куда ниже, чем у первой. Тем не менее шансы и у той, и у другой абсолютно равные – 1 к 1024.) С другой стороны, то, что за 10 бросков орел выпадет 4 раза, а не 10, куда вероятнее, ведь комбинаций с 4 орлами много, а с 10 – всего одна. Вот только «много» – это сколько? Подобная последовательность определяется количеством «орлиных» бросков, равным 4 из 10, соответственно, остальные броски должны закончиться выпадением решки. Количество способов определить, какие именно 4 из 10 бросков дадут нам орла, равно  (все равно что выбирать 4 разных шарика мороженого из 10 сортов). Значит, наш шанс, что из 10 попыток 4 раза выпадет орел, если бросать симметричную, абсолютно уравновешенную монетку, равен
(все равно что выбирать 4 разных шарика мороженого из 10 сортов). Значит, наш шанс, что из 10 попыток 4 раза выпадет орел, если бросать симметричную, абсолютно уравновешенную монетку, равен
 (все равно что выбирать 4 разных шарика мороженого из 10 сортов). Значит, наш шанс, что из 10 попыток 4 раза выпадет орел, если бросать симметричную, абсолютно уравновешенную монетку, равен
(все равно что выбирать 4 разных шарика мороженого из 10 сортов). Значит, наш шанс, что из 10 попыток 4 раза выпадет орел, если бросать симметричную, абсолютно уравновешенную монетку, равен
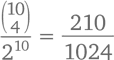
или примерно 20 % всех возможных комбинаций.
Отступление
Логично спросить, сколько можно собрать вазочек с 3 шариками из 10 сортов, если можно повторяться (10³/6 – ответ неправильный, это ведь даже не целое число). Наиболее простой способ – рассмотреть 3 отдельных случая, взяв за отправную точку количество разных сортов в вазочке. Очевидно, что в случае с 3 шариками одного сорта получится 10 вазочек. Из сказанного выше понятно, что в случае с 3 шариками 3 сортов получитсявазочек. А
вазочек будут с 2 сортами мороженого, ведь 2 сорта мы можем выбрать
способами. И лишь потом можно решать, какие 2 из 3 шариков будут именно этого сорта. Сложив все вместе, получим 10 + 120 + 90 = 220 вазочек.
Есть и другой способ прийти к этому ответу, не разбивая задачу. Каждую вазочку можно представить как комбинацию трех звездочек и девяти черточек. Если мы выбираем первый, второй и снова второй сорта, «перекодированная» вазочка будет выглядеть вот так:
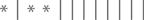
Второй, снова второй и седьмой сорта – вот так:
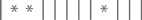
А комбинация

будет означать, что наш выбор пал на сорта третий, пятый и десятый. То есть вазочка – это набор из 3 звездочек и 9 черточек. Всего получается 12 символов, 3 из которых обязательно должны быть звездочками. Следовательно, возможных комбинаций у нас будетОбобщая, можно сказать, что количество способов выбрать k объектов из множества n при произвольном порядке и с возможностью повторения равно количеству способов сочетания k звездочек и n – 1 черточек –

Подсчет сочетаний необходим в большинстве задач, в которых большую роль играет случайность. Представим себе лотерею, в которой вам нужно угадать 5 различных чисел от 1 до 47. Дополнительно вы выбираете еще одно, МЕГАчисло от 1 до 27 (можно выбирать любое, в том числе и одно из тех, которые уже встречались в пятерке). У нас есть 27 вариантов выбора дополнительного числа, и  вариантов выбора основных 5 чисел. Таким образом, общее количество равно
вариантов выбора основных 5 чисел. Таким образом, общее количество равно
 вариантов выбора основных 5 чисел. Таким образом, общее количество равно
вариантов выбора основных 5 чисел. Таким образом, общее количество равно
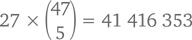
Другими словами, ваш шанс выиграть главный приз в такой лотерее – примерно 1 из 40 миллионов.
Теперь давайте переключим внимание на покер. Комбинация в покере – это обычно 5 карт из 52, составляющих колоду. Все они разные, выбраны случайно, порядок их значения не имеет. Следовательно, количество комбинаций равняется
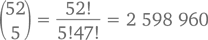
Комбинация из 5 карт одной и той же масти

называется флешем. Сколько всего может быть флешей? Чтобы посчитать, сначала выберем масть – 1 из 4 вариантов (давайте договоримся, что это будут пики). Сколько всего можно собрать комбинаций разных 5 карт этой масти? В колоде 13 пиковых карт. Значит, флешей всего
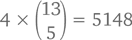
и наши шансы получить один из них составляют 5148/2 598 960, то есть примерно 1 к 500. Любители покера теперь могут вычесть из 5 148 4 × 10 = 40, чтобы узнать, какова вероятность, что собрать стрит-флеш – такой флеш, в котором карты одной масти идут подряд по старшинству.
При простом стрите масти в расчет не принимаются, главное – последовательный набор карт: Т-2-3-4-5 или 2-3-4-5-6, или…, или 10-В-Д-К-Т. Вот так, например:

Стрит может сложиться из 10 разных комбинаций (ценность которых определяется «ценностью» младшей карты). Определив ту из них, которая нужна нам (пусть будет 3-4-5-6-7), мы выбираем одну из 4 мастей, которой должны быть все карты. Следовательно, количество комбинаций стрита равняется
10 × 45 = 10 240
то есть почти в 2 раза выше, чем у флеша. А шанс его получить – 1 к 250. Именно поэтому флеш в покере ценится больше: его куда сложнее собрать.
Еще более ценен фул-хаус – 3 карты одного достоинства плюс 2 карты другого. Что-то вроде этого:

Чтобы подсчитать свои шансы на фул-хаус, нам сперва нужно выбрать необходимое нам достоинство, которое попадется нам трижды (13 вариантов), потом – то, которое попадется дважды (12 вариантов). Допустим, нам нужны 3 дамы и 2 семерки. Определимся с мастями. Получить нужных нам дам можно  способами, семерки –
способами, семерки – 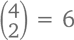 способами. Общее количество фул-хаусов, таким образом, равняется
способами. Общее количество фул-хаусов, таким образом, равняется
 способами, семерки –
способами, семерки – 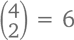 способами. Общее количество фул-хаусов, таким образом, равняется
способами. Общее количество фул-хаусов, таким образом, равняется13 × 12 × 4 × 6 = 3744
Следовательно, вероятность его собрать – 3744/2 598 960 или 1 к 700.
От фул-хаусов перейдем к двум парам. Здесь нам нужны две карты одного достоинства, еще две – другого, и последняя – третьего, например
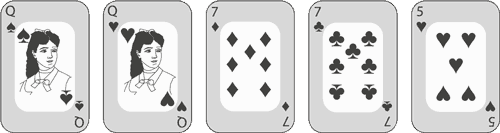
Пытаясь посчитать количество возможных пар, многие ошибочно начинают с 13 × 12, как в случае с фул-хаусами. Но теперь нам нужно немного другое, ведь здесь вероятность получить две семерки после двух дам – это абсолютно то же, что и получить двух дам после двух семерок. Поэтому правильно будет начать с  (имея в виду и семерки, и дам), потом выбрать новое достоинство для непарной карты (пусть это будет пятерка), затем выбрать масти. Количество комбинаций с двумя парами –
(имея в виду и семерки, и дам), потом выбрать новое достоинство для непарной карты (пусть это будет пятерка), затем выбрать масти. Количество комбинаций с двумя парами –
 (имея в виду и семерки, и дам), потом выбрать новое достоинство для непарной карты (пусть это будет пятерка), затем выбрать масти. Количество комбинаций с двумя парами –
(имея в виду и семерки, и дам), потом выбрать новое достоинство для непарной карты (пусть это будет пятерка), затем выбрать масти. Количество комбинаций с двумя парами –
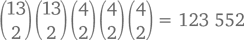
Появляются они в 5 % случаев.
Подробнее на всех вариантах раздач мы останавливаться не будем, но я попрошу вас взглянуть на следующие подсчеты и проверить, насколько они верны. Комбинаций с каре-, вроде  может быть
может быть
 может быть
может быть
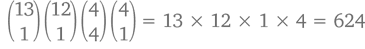
с тройкой-, например,  –
–
 –
–
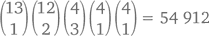
с одной парой – скажем, 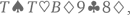 –
–
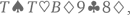 –
–
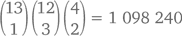
всего – 42 % всех возможных комбинаций.
Отступление
А сколько же может быть «пустых» комбинаций – без пар, без стритов и без флешей? Можете, конечно, сложить все числа, которые мы получили до этого и вычесть сумму изно я облегчу вам жизнь и просто дам ответ:
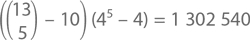
Первая часть – это количество комбинаций 5 карт разного достоинства за вычетом 10 последовательных (вроде 3-4-5-6-7). Следующая часть охватывает вероятные «расклады» этих 5 карт разного достоинства; для каждого достоинства у нас есть 4 варианта, но при этом мы должны исключить возможность того, что все они встретятся в одном «раскладе». Все это значит, что наши шансы собрать «пустую» комбинацию – 50,1 %. А еще это значит, что в 49,9 % случаев мы будем играть как минимум с одной парой.
А теперь вопрос, на который можно дать целых три прелюбопытных ответа, причем правильными из них будут сразу два! Сколько существует комбинаций, в которых есть как минимум один туз? Уверен, вас так и подмывает ответить 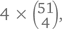 что, само собой, неправильно. Вы же исходите (и напрасно) из того, что сначала нужно выбрать туза (4 варианта), а потом собирать любые другие 4 карты из 51 оставшейся в колоде. Неправильно здесь то, что вы таким образом просчитываете некоторые комбинации (а именно – те, в которых больше одного туза) несколько раз. Например, комбинация
что, само собой, неправильно. Вы же исходите (и напрасно) из того, что сначала нужно выбрать туза (4 варианта), а потом собирать любые другие 4 карты из 51 оставшейся в колоде. Неправильно здесь то, что вы таким образом просчитываете некоторые комбинации (а именно – те, в которых больше одного туза) несколько раз. Например, комбинация 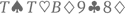 будет посчитана дважды: сначала для Т♠ в качестве первой, основной карты, а затем так же для
будет посчитана дважды: сначала для Т♠ в качестве первой, основной карты, а затем так же для  Правильный способ решить эту задачу – разбить ее на четыре задачи поменьше, в зависимости от того, сколько тузов будет в комбинации. Так, комбинаций именно с одним тузом будет
Правильный способ решить эту задачу – разбить ее на четыре задачи поменьше, в зависимости от того, сколько тузов будет в комбинации. Так, комбинаций именно с одним тузом будет 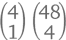 (сначала выбираем туза, потом – остальные 4 карты другого достоинства). Затем отдельно же просчитываем комбинации с двумя, тремя и четырьмя тузами. В результате получаем
(сначала выбираем туза, потом – остальные 4 карты другого достоинства). Затем отдельно же просчитываем комбинации с двумя, тремя и четырьмя тузами. В результате получаем
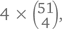 что, само собой, неправильно. Вы же исходите (и напрасно) из того, что сначала нужно выбрать туза (4 варианта), а потом собирать любые другие 4 карты из 51 оставшейся в колоде. Неправильно здесь то, что вы таким образом просчитываете некоторые комбинации (а именно – те, в которых больше одного туза) несколько раз. Например, комбинация
что, само собой, неправильно. Вы же исходите (и напрасно) из того, что сначала нужно выбрать туза (4 варианта), а потом собирать любые другие 4 карты из 51 оставшейся в колоде. Неправильно здесь то, что вы таким образом просчитываете некоторые комбинации (а именно – те, в которых больше одного туза) несколько раз. Например, комбинация 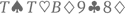 будет посчитана дважды: сначала для Т♠ в качестве первой, основной карты, а затем так же для
будет посчитана дважды: сначала для Т♠ в качестве первой, основной карты, а затем так же для  Правильный способ решить эту задачу – разбить ее на четыре задачи поменьше, в зависимости от того, сколько тузов будет в комбинации. Так, комбинаций именно с одним тузом будет
Правильный способ решить эту задачу – разбить ее на четыре задачи поменьше, в зависимости от того, сколько тузов будет в комбинации. Так, комбинаций именно с одним тузом будет 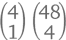 (сначала выбираем туза, потом – остальные 4 карты другого достоинства). Затем отдельно же просчитываем комбинации с двумя, тремя и четырьмя тузами. В результате получаем
(сначала выбираем туза, потом – остальные 4 карты другого достоинства). Затем отдельно же просчитываем комбинации с двумя, тремя и четырьмя тузами. В результате получаем
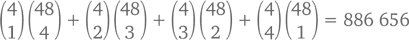
Но проще всего будет пойти от обратного. Сначала посчитаем количество комбинаций без туза (это легче легкого) –  А количество комбинаций по крайней мере с одним тузом, таким образом, –
А количество комбинаций по крайней мере с одним тузом, таким образом, –
 А количество комбинаций по крайней мере с одним тузом, таким образом, –
А количество комбинаций по крайней мере с одним тузом, таким образом, –
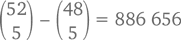
Я уже говорил чуть выше, что «цена» комбинаций в покере зависит от частоты их появлений: чем реже комбинация, тем она «ценнее». То есть если шансов собрать одну пару больше, чем сразу две, одна пара ценится куда меньше двух. Вот «стоимость» всех комбинаций, от меньшей к большей:
ПараДве парыТройкаСтритФлешФул-хаусКаре (или «четверка»)Стрит-флеш
На этот случай есть эффективная «запоминалка»: «Раз, два, три, стрит, флеш; два-три, четыре, стрит-флеш» (где «два-три» – это фул-хаус).
А теперь предположим, что в колоде появились джокеры. Всего карт у нас становится 54, причем джокеры (всего их два) могут «превращаться» в карту любой масти и любого достоинства – в зависимости от того, что вам нужно для наилучшей комбинации. То есть если у вас на руках 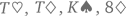 и джокер, разумнее всего будет посчитать его тузом, чтобы получилась тузовая тройка. Можно «превратить» джокера и в короля, конечно, но тогда у вас будет две пары, что хуже, чем тройка.
и джокер, разумнее всего будет посчитать его тузом, чтобы получилась тузовая тройка. Можно «превратить» джокера и в короля, конечно, но тогда у вас будет две пары, что хуже, чем тройка.
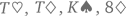 и джокер, разумнее всего будет посчитать его тузом, чтобы получилась тузовая тройка. Можно «превратить» джокера и в короля, конечно, но тогда у вас будет две пары, что хуже, чем тройка.
и джокер, разумнее всего будет посчитать его тузом, чтобы получилась тузовая тройка. Можно «превратить» джокера и в короля, конечно, но тогда у вас будет две пары, что хуже, чем тройка.

Но здесь-то и начинается самое интересное. Следуя традиционному порядку карт, мы можем посчитать эту комбинацию и как тройку, и как две пары, а можем – только как тройку, исключив ее из числа двух пар. Последнее выглядит наиболее разумно, но ведь это значит, что общее количество комбинаций с тройками значительно увеличивается, а с двумя парами – уменьшается, что превращает последние в более редкие. Мы, конечно, можем сказать, что теперь две пары имеют бóльшую ценность, но проблему этим не решишь: она всего лишь «перевернется вверх ногами», ведь количество двух пар увеличится, а количество троек – уменьшится. Из этого всего следует странный на первый взгляд вывод, сделанный математиком Стивом Гэдбойсом в 1996 году: при игре в покер с джокерами невозможно ранжировать «ценность» комбинаций по частоте их появления.
Назад: Правило суммы и произведения
Дальше: Закономерности треугольника Паскаля