На рис. П1 схематично представлены платежные функции отдельных опционов колл и пут для покупателя (длинные опционы)и продавца (короткие опционы). Сплошными линиями показаны платежные функции на дату исполнения, прерывистыми линиями – на некоторою промежуточную дату, предшествующую дате исполнения. При заданной цене базового актива позиция покупателя опциона тем больше, чем больше времени остается до истечения (прерывистые линии на рисунках расположены выше сплошных линий). И наоборот, чем ближе дата истечения, тем дороже позиция продавца опциона (прерывистые линии на рисунках расположены ниже сплошных линий). Это объясняется тем, что в стоимости опциона присутствует как внутренняя стоимость, так и временная стоимость. Последняя непрерывно уменьшается по мере приближения даты истечения (это явление называется временным распадом).

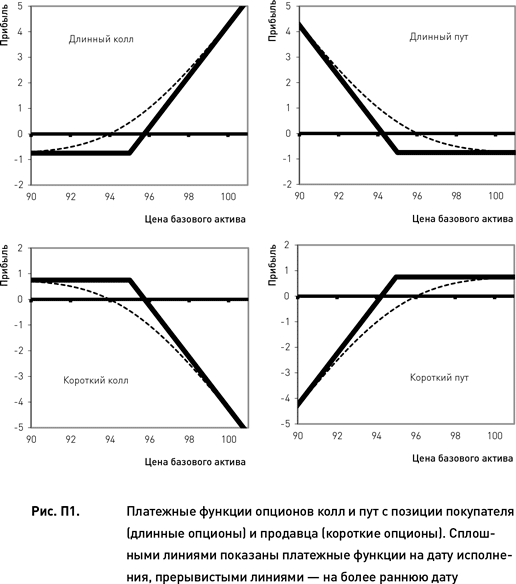
Из рис. П1 следует, что покупатель опциона колл получает теоретически неограниченную прибыль при росте цены базового актива и ограниченный убыток в случае ее падения (максимальный убыток ограничен величиной премии, уплаченной при покупке опциона). Покупатель опциона пут получает теоретически неограниченную прибыль при падении цены базового актива и ограниченный убыток в случае ее роста. В обоих случаях максимальный убыток ограничен величиной премии, уплаченной при покупке опциона.

Платежные функции коротких опционов являются зеркальным отражением платежных функций длинных опционов (рис. П1). Прибыли продавцов опционов лимитированы размером получаемой премии, а их убытки теоретически безграничны и зависят от силы ценового движения базового актива. Чем больше вырастет цена базового актива, тем большим будет убыток коротких коллов. Соответственно, чем больше цена снизится, тем большим будет убыток коротких путов.