Книга: Опционы: Разработка, оптимизация и тестирование торговых стратегий
Назад: 5.4. Построение надежной системы тестирования
Дальше: 5.6. Построение эффективной системы бэктестинга: вызовы и компромиссы
5.5. Оценка прибыльности
Оценка прибыльности стратегии является многокритериальной задачей. Не существует единого показателя, с помощью которого можно было бы выразить эффективность стратегии или сравнить ее с другой стратегией. Вместо этого существует целый ряд универсальных показателей, используемых при бэктестинге любых стратегий, независимо от применяемых в торговле инструментов. Хотя эти показатели общеизвестны, их применение и методика расчета для опционных стратегий имеет свою специфику. Помимо универсальных показателей, существуют также показатели, применяемые исключительно для оценки опционных стратегий.
5.5.1. Единичное событие и элементарный период времени
Для расчета показателей эффективности стратегий необходимо дать строгое определение единичного события и элементарного периода времени, для которых производится оценка прибыльности стратегии.
В качестве единичного события может быть принята каждая отдельно взятая сделка по определенному опционному контракту либо совокупность сделок, относящихся к определенному контракту и исполненных в течение одного дня. Кроме того, единичным событием может считаться совокупность всех сделок, исполненных в течение одного дня для построения определенной опционной комбинации. При торговле обычными инструментами в качестве единичного события, как правило, используется каждая отдельно взятая сделка. Выбор единичного события для стратегий, ориентированных на торговлю опционами, зависит от особенностей стратегии. В большинстве случаев при бэктестинге опционных стратегий оценивается не каждая отдельная сделка, а совокупность сделок, относящихся к одной комбинации или к одному базовому активу.
При определении элементарного периода времени существенным фактором является то, что итог многих сделок, связанных с опционами может быть определен только на момент их экспирации. Многие опционные стратегии основываются на выборе торговых вариантов с помощью критериев, оценивающих опционы в момент их покупки или продажи, ориентируясь на дату экспирации. Это связано не только с удобством применения математического аппарата ценообразования опционов, но и большей определенностью цен опционов в момент экспирации. Традиционным временем экспирации опционов на CBOE (основной опционной биржи) является третья пятница каждого месяца. Поэтому для стратегий, торгующих на рынке опционов на акции, возникает естественная месячная периодичность измерений прибыльности, связанная со стандартным временем экспирации. Для таких стратегий элементарный период времени составляет один месяц.
Для стратегий, работающих с опционами далеких серий, момент экспирации уже не будет играть такую ключевую роль, как для опционов ближайших серий. В этом случае возрастает роль других временных ориентиров, использование которых более обоснованно для промежуточных оценок текущего портфеля. В последнее время вводятся биржами и получают растущую популярность опционы с недельной периодичностью экспираций. Для стратегий, работающих с ними, удобным будет недельный элементарный период времени.
Стратегии с применением техник динамического хеджирования могут сопровождаться большой интенсивностью сделок с ликвидным базовым активом и редкими сделками по опционам. В таких стратегиях с большой частотой сделок и моментов принятия решений удобным временем оценки показателей стратегии могут быть дневные (и даже более дробные) периоды времени.
5.5.2. Обзор показателей прибыльности стратегии
Предположим, что требуется оценить эффективность стратегии на интервале времени τ = [T0, TN] с последовательностью промежуточных моментов времени (T0, T1…, TN). Для простоты будем измерять время в днях. Тогда длина интервала τ составит TN – T0 дней или в годах примерно ΔT = (TN – T0)/A, где A = 365,25 календарных дней. Обозначим через (E0, E1…, EN) последовательность значений величины капитала, который оценивается в каждый из моментов времени (T0, T1…, TN) по заложенному в систему бэктестинга алгоритму. Обычно для оценки капитала используется ликвидационная стоимость всех позиций стратегии, рассчитанная по ценам закрытия соответствующего дня, включая свободные денежные средства. Итоговый доход стратегии составит величину ΔE = EN – E0.
Показатели доходности
Будем рассматривать два вида доходности, соответствующих двум подходам к управлению капиталом (имеется ввиду первый уровень системы управления капиталом, см. главу 4), – с постоянной суммой, инвестируемой в стратегию в каждый период времени, и с реинвестицией.
Первый подход удобен для анализа среднего результата серии однотипных портфелей. Этот случай хорошо подходит для стратегии, основанной на продаже волатильности незадолго до экспирации, когда каждая экспирации порождает один отдельный портфель. При этом для каждого элементарного периода времени используется одна и та же сумма E0. Для случая управления капиталом с постоянной суммой инвестиций будем пользоваться линейной годовой доходностью:
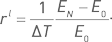
Эта величина соответствует средней арифметической доходности указанной серии, приведенной к годовому масштабу.
Второй подход к управлению капиталом более удобен для сравнения результатов стратегии с эталонным доходом типа непрерывно начисляемой процентной ставки (например, безрискового актива) или с определенным индексом (например, S&P 500). В таком случае следует пользоваться экспоненциальной годовой доходностью:
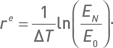
Экспоненциальная доходность соответствует средней геометрической доходности, приведенной к годовому масштабу.
Моменты времени, когда производятся измерения капитала, будем связывать с моментами экспирации опционов. В этом случае мы приходим к серии месячных прибылей и убытков. Пусть N – число месяцев в периоде, на котором производится бэктестинг стратегии. В линейном случае предполагается, что стартовый капитал каждого месяца равен Ei−1, а инвестируемый капитал всегда равен E0. Тогда прибыль i-го месяца pli = Ei − Ei−1, средняя прибыль за месяц  средняя доходность
средняя доходность 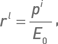 доходность i-го месяца
доходность i-го месяца  В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i-го месяца
В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i-го месяца  в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность
в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность 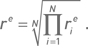
 средняя доходность
средняя доходность 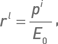 доходность i-го месяца
доходность i-го месяца  В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i-го месяца
В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i-го месяца  в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность
в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность 
Для наборов {pl1, pl2…, plN}, {rl1, rl2…, rlN} и {re1, re2…, reN} можно рассчитать простые статистики, имеющие непосредственное значение для оценки стратегии инвестором. Максимальная месячная прибыль 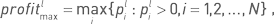 максимальная линейная месячная доходность
максимальная линейная месячная доходность 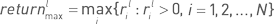 и максимальная экспоненциальная месячная доходность
и максимальная экспоненциальная месячная доходность 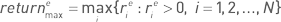 характеризуют один наиболее удачный месяц.
характеризуют один наиболее удачный месяц.
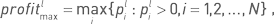 максимальная линейная месячная доходность
максимальная линейная месячная доходность 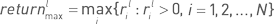 и максимальная экспоненциальная месячная доходность
и максимальная экспоненциальная месячная доходность 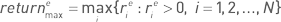 характеризуют один наиболее удачный месяц.
характеризуют один наиболее удачный месяц.Противоположные по смыслу величины – максимальный месячный убыток в абсолютном и относительном (аналогично доходности) измерении – имеют большое значение, поскольку размеры этих величин могут оказаться неприемлемыми, и тогда такой вариант стратегии придется отвергнуть. Даже высокодоходная стратегия, имеющая на длительном интервале всего один убыточный месяц, может быть отвергнута, если этот убыток превышает определенную пороговую величину. Максимальный месячный убыток в абсолютном выражении имеет смысл только в линейном случае и определяется как 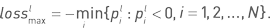 Аналогично определяются относительные величины для линейного случая как
Аналогично определяются относительные величины для линейного случая как  и для экспоненциального случая как
и для экспоненциального случая как 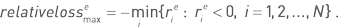
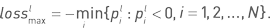 Аналогично определяются относительные величины для линейного случая как
Аналогично определяются относительные величины для линейного случая как  и для экспоненциального случая как
и для экспоненциального случая как 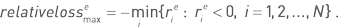
Общепринятым показателем риска является стандартное отклонение доходностей, зафиксированных на интервале τ. Чаще всего данный показатель рассматривается не сам по себе, а в совокупности со средней доходностью (см. ниже раздел, посвященный коэффициенту Шарпа).
Несложно также ввести и другие показатели: число прибыльных месяцев, число убыточных месяцев, средняя прибыль прибыльных месяцев, средний убыток убыточных месяцев, максимальное число прибыльных месяцев подряд, максимальное число убыточных месяцев подряд и т. п.
Максимальная просадка
Одним из наиболее популярных показателей риска автоматизированных торговых стратегий является максимальная просадки капитала. Просадка в момент времени Т – это величина, равная разнице между текущим значением капитала Е(Т) и максимальным значением капитала на всем предшествующем интервале времени: 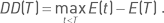 Для интервала исследования стратегии τ максимальная просадка вычисляется как
Для интервала исследования стратегии τ максимальная просадка вычисляется как 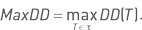
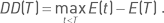 Для интервала исследования стратегии τ максимальная просадка вычисляется как
Для интервала исследования стратегии τ максимальная просадка вычисляется как 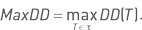
С понятием просадки тесно связан показатель длительности просадки, измеряющий время, проходящее от момента установления локального максимума капитала до его пробития. Обозначим через lmax момент установления максимального значения капитала, а через E(tmax) обозначим значение капитала в момент tmax. Если в текущий момент времени T значение капитала превысило предыдущее максимальное значение, то есть E(T) > E(Tmax), то фиксируется продолжительность просадки как разница T – tmax. Максимальную для стратегии продолжительность просадки можно рассматривать как дополнительный негативный показатель качества стратегии.
Приведенные два показателя – максимальная просадка капитала и максимальная длительность просадки – представляют собой наиболее важные в эмоциональном плане характеристики риска. Неприемлемые значения этих показателей в реальной торговле нередко служат причиной отказа от продолжения использования прибыльных стратегий. Между тем периодическое возникновение просадок является нормальным явлением для многих успешных стратегий. Следует отметить, что психологический эффект, испытываемый инвестором, зависит от того, насколько успешна была стратегия до начала просадки. Но с точки зрения бэктестинга, большая просадка плоха независимо от момента ее возникновения. Если стратегия допускает просадку, то теоретически она может начаться непосредственно после запуска реальной торговли. Это может полностью разрушить торговый счет.
Основной недостаток данных показателей заключается в том, что они выражают величину и длительность возможных максимальных убытков, но при этом никак не оценивают вероятность наступления такого события. Между тем убыток определенной величины, зафиксированный при тестировании стратегии на годичном периоде истории, указывает на гораздо больший риск, чем если такой же убыток обнаруживается при тестировании на 10-летней базе исторических данных. Поэтому степень рискованности стратегии, оцениваемую на основании максимальной просадки, следует взвешивать по протяженности периода тестирования.
Коэффициент Шарпа
Поскольку существует прямая положительная связь доходности и риска, очень удобными являются показатели, максимизация которых позволяет решать одновременно две задачи – максимизацию доходности и снижение риска. На интервале тестирования стратегии разработчик получает выборку из N значений доходности. Чем ближе элементы выборки друг к другу, и, следовательно, к их среднему значению, тем ровнее и стабильнее выглядит кривая роста капитала. Стремление к одновременной максимизации средней доходности и минимизации стандартного отклонения доходностей реализуется путем использования коэффициента Шарпа, широко применяемого практически во всех системах бэктестинга.
В оригинале коэффициент Шарпа выглядит как отношение между математическим ожиданием доходности и ее стандартным отклонением. Причем доходность измеряется за вычетом некой базовой доходности, например ставки безрискового актива. Мы предпочитаем использовать более практичный вариант коэффициента, пренебрегающий базовой доходностью (использование базовой доходности лишь усложняет вычисления, не принося дополнительной пользы при выборе наилучшей стратегии).
Коэффициент Шарпа для оценки стратегии в системе бэктестинга будем оценивать как SR = r/σ, где r – средняя доходность серии из N доходностей, σ – среднеквадратичное отклонение этих доходностей. В экспоненциальном случае мы применяем среднюю геометрическую доходность (re), а в линейном случае – среднюю арифметическую доходность (rl). Среднеквадратичное отклонение вычисляется по стандартной формуле
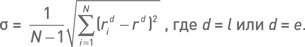
В итоге получается безразмерный показатель, не зависящий от длительности периода бэктестинга. На наш взгляд, коэффициент Шарпа – это один из самых удобных показателей бэктестинга.
Главным недостатком коэффициента Шарпа является то, что в нем никак не учитывается порядок, в котором чередуются прибыльные и убыточные месяцы. Из формул, применяемых для его вычисления, видно, что мы можем перемешать слагаемые в любом порядке без изменения результата. Это значит, что один и тот же коэффициент Шарпа может быть как у стратегии с равномерно растущим капиталом, так и у стратегии с неприемлемой величиной максимальной просадки. В хорошей стратегии не должно быть больших последовательностей следующих друг за другом убыточных месяцев. Эта проблема решается совместным использованием коэффициента Шарпа и описанных выше показателей риска (в частности, максимальной просадки).
Profit/Loss-фактор
Часто при бэктестинге торговых стратегий используется показатель, называемый profit/loss-фактор, рассчитываемый как отношение суммы прибылей всех прибыльных сделок к сумме убытков всех убыточных сделок. Считается, что для эффективной стратегии profit/loss-фактор должен быть не менее 2. Для стратегий, ведущих торговлю опционами, такой подсчет соотношений убытков и прибылей имеет свою специфику. Данный показатель полезен и информативен для оценки стратегий, в которых сделки производятся последовательно одна за другой и имеют однотипный характер. Например, в простейшем случае торговли одной акцией – это последовательность открытий и закрытий позиций. Тогда profit/loss-фактор вполне адекватно отражает качество генератора сигналов на покупку и продажу. В опционной торговле этот показатель имеет для каждой стратегии свой смысл, поскольку само множество сделок не является однородным.
Поясним сказанное на двух примерах. Рассмотрим классическую стратегию торговли волатильностью с помощью дельта-нейтрального хеджирования. Простейший вариант реализации такой стратегии заключается в покупке (или продаже) некоего опциона, после чего производятся многократные покупки и продажи его базового актива в разных количествах (будем называть всю совокупность таких сделок «игрой»). В такой ситуации нет никакого смысла анализировать структуру прибылей и потерь по отдельным сделкам. Смысл имеет только итоговый результат всей игры, определяющийся после закрытия отдельных позиции. Поэтому, вместо результатов единичных сделок при подсчете profit/loss-фактора, необходимо использовать суммы всех прибыльных и убыточных игр.
Второй пример связан со стратегией продажи волатильности. Предположим, что алгоритм стратегии предусматривает следующий порядок действий. Каждый день для каждого базового актива строятся комбинации стрэнгл или стрэддл из одного короткого опциона колл и одного короткого опциона пут «около денег». Все множество комбинаций упорядочивается по специальному критерию, и определенное количество комбинаций продается в соответствии с принятым методом управления капиталом. Как и в предыдущем примере, оценку структуры прибылей и убытков такой стратегии не имеет смысла рассчитывать по отдельным сделкам. В этом случае можно оперировать либо прибылями и убытками отдельных комбинаций, либо результатом всей позиции, образованной в один день, либо результатами торговли за один экспирационный цикл.
Для того чтобы использование profit/loss-фактора было корректным, необходимо правильно определить единичное событие (см. раздел 5.5.1). В первом примере в качестве единичного события должна быть принята вся совокупность сделок, относящихся к определенному базовому активу. Во втором случае единичным событием может считаться совокупность всех сделок, исполненных в течение одного дня (или всего экспирационного цикла), для построения определенной опционной комбинации.
Консистентность
Стратегия является консистентной (стабильной), если прибыльные и убыточные сделки не сконцентрированы в определенные периоды, а распределены более-менее равномерно по всему периоду тестирования. При неравномерном распределении периоды роста капитала сменяются периодами падения, длительность и глубина которых определяется степенью этой неравномерности. В опционной торговле не всегда можно выделить четкую последовательность сделок, следующих одна за другой. Как правило, позиции, открытые в последовательные моменты времени, не закрываются в том же порядке. Поэтому для опционных стратегий понятие консистентности стратегии следует связывать с фактической кривой капитала (а не с отдельными сделками), получающегося в процессе бэктестинга.
Идеальная стратегия – это стратегия с постоянным доходом и нулевыми просадками, дающая прибыль на каждом элементарном отрезке времени. В линейном случае график ее капитала имеет вид прямой с наклоном, характеризующим ее доходность. В экспоненциальном случае графиком идеальной стратегии должен быть график экспоненты, показателем которой является нормированная доходность стратегии (если перейти к графику логарифма капитала, то мы получим все тот же прямолинейный вид, что и в предыдущем случае). Хорошим показателем стабильности является мера отклонения графика капитала (или логарифма капитала) от прямой.
Пусть последовательность X = {X(T), T = T0, T0 + 1…, TN} содержит серию измерений капитала или логарифма капитала на интервале прогонки τ. Через крайние точки этой последовательности проходит прямая линия: 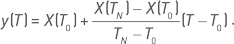 Мера отклонения исходной последовательности от нее может быть задана как сумма квадратов:
Мера отклонения исходной последовательности от нее может быть задана как сумма квадратов:
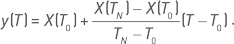 Мера отклонения исходной последовательности от нее может быть задана как сумма квадратов:
Мера отклонения исходной последовательности от нее может быть задана как сумма квадратов:

Чем меньше значение этого показателя, тем ближе вид кривой капитала стратегии к идеальному.
5.5.3. Пример бэктестинга опционной стратегии
Рассмотрим в качестве примера результаты бэктестинга стратегии, основанной на продажах опционов на SPY и хеджировании позиции покупкой опционов на VIX. Стратегия использует следующий алгоритм: в заданный день до экспирации продается стрэнгл на SPY и покупается колл на VIX следующей серии в объемах, определяемых заложенным в стратегию алгоритмом управления капиталом. Короткая позиция выкупается в заданный день перед экспирацией. Длинный опцион на VIX сохраняется до экспирации. Параметры стратегии:
• день открытия позиции относительно ближайшей экспирации;
• день выкупа коротких опционов;
• соотношение объемов стрэнглов на SPY и коллов на VIX;
• доля капитала в текущей позиции;
• параметр, определяющий расстояние между страйками.
Визуальный анализ
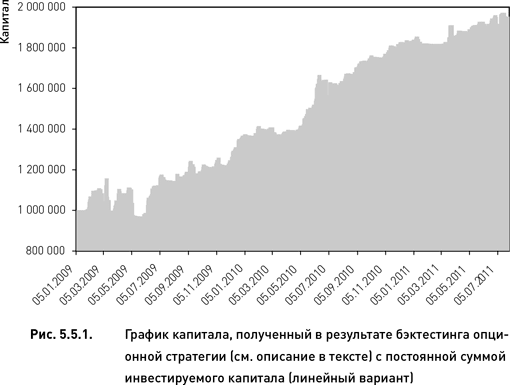
Как правило, анализ результатов бэктестинга начинается с визуализации базовых показателей на графиках в виде кривых, изменяющихся во времени в процессе прогонки по интервалу τ. Наиболее информативным является график капитала. На рис. 5.5.1 показан график, полученный в результате бэктестинга одного из вариантов стратегии. Мы выбрали один из лучших вариантов, дающий достаточно ровный и устойчивый рост капитала. Визуальный анализ графика указывает на то, что рассматриваемый вариант стратегии приемлем и заслуживает дальнейшего более детального изучения.
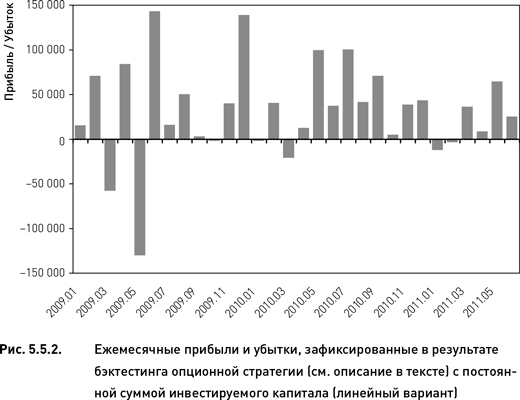
Обычно график капитала строится с ежедневными оценками (как показано на рис. 5.5.1). Это позволяет оценить внутримесячные колебания и просадки. Однако в случае опционных стратегий часто возникает необходимость представить доходность с привязкой к стандартным моментам экспирации. В таких случаях удобной формой представления является график, показывающий ежемесячные прибыли и убытки (если элементарный период времени составляет один месяц). На рис. 5.5.2 показан график для стратегии, использованной в нашем примере. Такое представление доходности позволяет сразу увидеть, что из 31 месяца, охваченного периодом бэктестинга, большинство были прибыльными и только два месяца принесли существенный убыток. Хотя эти два сильно убыточных месяца пришлись на начальный период тестирования, они не привели к разорению стратегии, что является серьезным показателем ее высокой эффективности.
Анализ расчетных показателей
Ниже приведены расчеты различных показателей для линейного варианта стратегии (с постоянной суммой инвестируемого капитала). Некоторые показатели рассчитаны сразу для двух временных интервалов: месяцев (что соответствует экспирационным циклам) и дней (поскольку день приходится рассматривать как элемент времени, на котором необходима достаточная устойчивость к негативным рыночным событиям).
Период тестирования стратегии: 01.01.2009–31.07.2011 г.
Стартовый капитал: E0 = 1 000 000.
Число календарных дней: d = 938.
Число торговых дней: t = 648.
Число месяцев: m = 31.
Суммарная прибыль: P = 1 953 594 – 1 000 000 = 953 594.
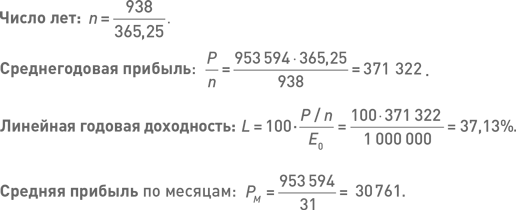
Среднеквадратичное отклонение месячных прибылей:
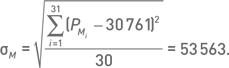
Коэффициент Шарпа для месячных данных:
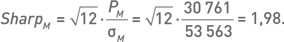

Среднеквадратичное отклонение дневных прибылей:
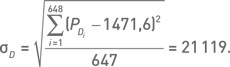
Коэффициент Шарпа для дневных данных:
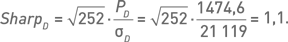
Максимальная просадка состоялась 18.03.2009, когда текущий максимум капитала 1 157 537, установленный 11.03.2009, снизился до 818 733. Величина просадки составила 338 803.
Длительность максимальной просадки (то есть длина периода до установления нового максимального значения капитала) составила 78 дней. Она оказалась самой продолжительной на всем периоде тестирования.
Доля прибыльных сделок (сделкой считается совокупность всех торговых операций, относящихся к определенной комбинации, и выполненных в течении одного дня): 53,6 %.
Доля прибыльных месяцев: 76,6 %.
Максимальное число прибыльных месяцев, следующих подряд: девять месяцев.
Максимальное число убыточных месяцев, следующих подряд: два месяца.
Среднее число прибыльных месяцев, следующих подряд: 3,3 месяца.
Среднее число убыточных месяцев, следующих подряд: 1,2 месяца.
Суммарный доход прибыльных сделок: grossprofit = 2 684 032.
Суммарный убыток убыточных сделок: grossloss = 1 730 438.
Profit/Loss-фактор, рассчитанный по отдельным сделкам: grossprofit / grossloss =1,55.
В данной стратегии, как и во многих других опционных стратегиях, Profit/Loss-фактор, рассчитанный по отдельным сделкам, не является полностью корректным (см. объяснения в разделе 5.5.2). Поэтому более информативным будет аналогичное отношение, рассчитываемое для прибылей и убытков отдельных месяцев. Сам алгоритм стратегии предусматривает подобный подход, поскольку динамически наращиваемая позиция от первого дня торговли каждого месяца до закрытия коротких позиций перед экспирацией, является логичным единичным событием, подобно отдельной сделке в стратегиях с линейными инструментами (акциями, фьючерсами). Profit/Loss-фактор, рассчитанный на основании месячных данных, оказался значительно выше, чем тот же показатель, рассчитанный по отдельным сделкам: 1 176 797 / 223 203 = 5,3.
Назад: 5.4. Построение надежной системы тестирования
Дальше: 5.6. Построение эффективной системы бэктестинга: вызовы и компромиссы

