Книга: Опционы: Разработка, оптимизация и тестирование торговых стратегий
Назад: 3.1. Особенности оценки риска опционов
Дальше: 3.3. Взаимозависимость индикаторов риска
3.2. Индикаторы риска
Для оценки риска отдельных опционов и опционных портфелей могут использоваться как традиционные показатели, такие как VaR, так и специализированные индикаторы, разрабатываемые специально для этих целей. Хотя оценка опционных портфелей с помощью показателей, обычно используемых для линейных активов, технически возможна, необходимо крайне осторожно подходить к интерпретации получаемых с их помощью данных. Кроме того, такие показатели можно использовать только в качестве вспомогательных инструментов оценки риска. Основными же должны является показатели, разработанные с учетом опционной специфики. Для получения полного представления о риске создаваемого портфеля желательно использовать несколько показателей одновременно. При этом разные показатели должны как можно меньше коррелировать между собой. Это позволит сформировать набор уникальных индикаторов риска, каждый из которых будет дополнять, а не дублировать информацию, содержащуюся в других показателях.
В этом разделе мы рассмотрим четыре индикатора риска. Начнем мы с показателя VaR и объяснения, каким образом данный индикатор может быть рассчитан для опционного портфеля. Затем мы опишем три специализированных индикатора, разработанных специально для оценки риска опционов. Особое внимание будет уделено показателю «индексная дельта».
3.2.1. Value at Risk (VaR)
Напомним, что VaR представляет собой оценку убытка, который с заданной вероятностью не будет превзойден в течение заданного периода времени (в дальнейших примерах мы будем использовать вероятность 95 %). Для портфеля, состоящего только из базовых активов, этот показатель может быть рассчитан аналитически. В случае портфеля, состоящего из нелинейных инструментов, необходимо применять метод Монте-Карло. Для этого на основании стандартного отклонения доходностей базового актива строится функция плотности вероятности логнормального (или другого) распределения, которая используется для генерирования множества вариантов цены базового актива. Далее для каждого варианта цены вычисляется платежная функция опциона и на основании этих данных рассчитывается VaR. Эта же методика может использоваться для расчета VaR портфеля опционов с учетом корреляций между различными базовыми активами.
Используя данную методику, необходимо помнить, что VaR обладает целым рядом существенных недостатков (Tsudikman et. al., 2011), проявляющихся наиболее ярко, когда он используется для оценки риска нелинейных активов.
До недавнего времени в среде профессиональных участников рынка бытовало мнение, что VaR адекватно выражает уровень риска любых инвестиционных портфелей независимо от их состава и структуры. Однако мировой финансовый кризис, разразившийся в 2007 г., убедительно продемонстрировал несоответствие прогнозов, основанных на VaR, реальным убыткам. Причина расхождения прогнозов и реальности состояла в том, что за последние 20 лет финансовые рынки претерпели кардинальные изменения, выразившиеся в развитии сложных финансовых технологий и переносе акцентов с простых линейных активов на производные инструменты (многие из которых являются нелинейными). При этом доля нелинейных активов, среди которых не последнее место занимают опционы, в структуре активов крупных финансовых институтов неуклонно возрастала. Несмотря на это, механизмы оценки риска оставались прежними либо существенно отставали в своем развитии.
При разработке автоматизированных торговых систем недопустимо использование односторонней системы прогнозирования риска, основанной исключительно на VaR или других показателях, рассчитываемых на основе стандартного отклонения. Полноценная система управления рисками должна включать в себя целый комплекс оценочных алгоритмов, базирующихся на разных принципах и учитывающих специфические особенности опционов.
3.2.2. Индексная дельта
Индексная дельта характеризует чувствительность опционного портфеля к колебаниям широкого рынка. Этот показатель позволяет дать количественное выражение изменению стоимости портфеля, происходящему при небольшом изменении индекса. Индексная дельта может использоваться для оценки риска и управления сложно-структурированным портфелем так же, как это делается с обычной дельтой для портфелей, состоящих из опционов на один базовый актив. Кроме того, индексная дельта может применяться для создания дельта-нейтральных портфелей (как было описано в главе 1), а также для корректировки позиций в целях сохранения дельта-нейтральности на протяжении всего периода существования портфеля.
Алгоритм
Алгоритм вычисления индексной дельты можно представить в виде последовательности следующих процедур.
1. Строится регрессионная модель зависимости цены каждого базового актива (чьи опционы входят в состав портфеля) от индекса. Для этого необходимо выбрать горизонт истории, на котором строятся модели.
2. С помощью регрессионных моделей, построенных на шаге (1), рассчитываем значение цены каждого базового актива, к которому приводит изменение индекса на один пункт или на другую небольшую величину (например, на 0,1 %).
3. Определяем справедливую стоимость каждого входящего в портфель опциона при условии, что цена его базового актива равна значению, полученному на шаге (2). Для этого необходимо воспользоваться одной из моделей ценообразования, заменяя в ее формуле текущую цену базового актива соответствующим расчетным значением.
4. Вычисляем приращение цены каждого входящего в портфель опциона, произошедшее в результате изменения цены его базового актива на один пункт. Приращение цены равно разности расчетной стоимости, полученной на шаге (3), и текущей рыночной цены опциона.
5. Рассчитываем значение индексной дельты путем суммирования всех приращений, полученных при исполнении процедур на шаге (4).
Расчет индексной дельты
Рассмотрим портфель, состоящий из опционов на различные активы. Пусть {O1, O2, O3…, ON} представляет множество составляющих портфель опционов, причем базовым активом опциона Oi является Ai. Если при j ≠ k активы Ai и Ak совпадают, то речь может идти об опционной комбинации, построенной в рамках определенной торговой стратегии (например, стрэнгл, стрэддл, календарный спред и т. д.). В принципе комбинации могут состоять из неограниченного количества разных опционов, относящихся к одному базовому активу, а портфель – из неограниченного количества комбинаций.
Для каждого опциона Oi, входящего в состав портфеля, мы имеем опционную дельту:
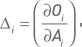
где величины δO1 и δA1 обозначают малые изменения цен опциона и его базового актива соответственно. Это выражение дает наглядное представление о дельте как о скорости изменения цены опциона по отношению к изменению цены его базового актива.
Вычисление дельты Di одного опциона не представляет сложности и реализовано во многих компьютерных программах. Переходя к портфелю, состоящему из опционов на разные базовые активы, мы не можем суммировать дельты разных опционов, поскольку они являются частными производными функций (премий) по разным независимым переменным (ценам акций). Как было сказано выше, эту задачу мы будем решать, вычисляя скорость изменения стоимости опциона по отношению к индексу, а не к отдельным базовым активам. Определим дельту по отношению к индексу как производную цены опциона по значению индекса:
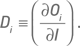
Эту индексную дельту можно также представить в следующем виде:

Величина  так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
 так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
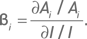
Произведя несложные преобразования

подставим полученное выражение в формулу (3.2.1). Получаем индексную дельту одного опциона:

где Δi – дельта опциона относительно его базового актива. Количество единиц опциона Oi, входящее в состав портфеля, обозначим через xi. Для вычисления индексной дельты Dportfolio всего портфеля суммируем дельты отдельных опционов, входящих в портфель с учетом их количества:
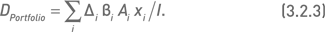
Индексную дельту, рассчитанную по формуле (3.2.3), можно интерпретировать как изменение стоимости портфеля при изменении значения индекса на один пункт. Более удобно выражать изменение стоимости портфеля при изменении индекса на некую процентную величину. Это позволит оценить чувствительность портфеля к относительным изменениям индекса. Например, простое преобразование формулы (3.2.3) позволяет вычислять «процентную индексную дельту» для изменения индекса на 1 %:
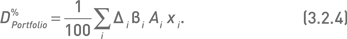
Пример расчета индексной дельты
В качестве примера рассчитаем величину индексной дельты небольшого портфеля, состоящего из опционов на американские акции. Вычисления будем производить относительно индекса S&P 500, хотя для этих целей может использоваться любой другой индекс. В таблице 3.2.1 представлен портфель, состоящий из семи коротких стрэддлов, взятых в разных количествах (приблизительно обратно пропорциональных ценам соответствующих акций). Портфель был создан 2 января 2009 г. из опционов с ближайшей датой экспирации (16 января 2009 г.). Текущее значение индекса на 2 января 2009 г. составляло 931,8. Коэффициенты бета акций рассчитаны по ценам дневного закрытия на горизонте истории, равном 120 торговым дням. Дельты опционов вычислены по формулам Блэка – Шоулса с безрисковой ставкой, равной 3,3 %.
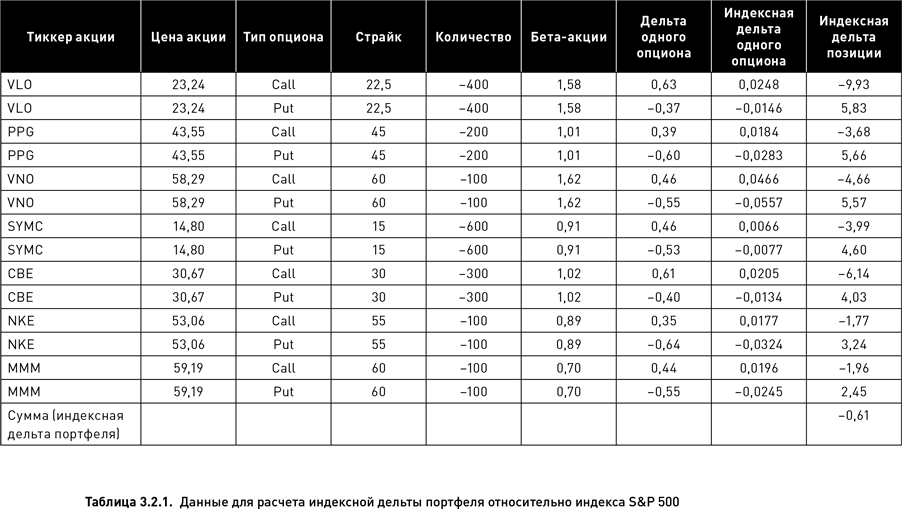
В предпоследней колонке таблицы 3.2.1 приведены индексные дельты одного опциона, рассчитанные по формуле (3.2.2). Например, для колл на акцию VLO получаем Di = (23,24 × 1,58 × 0,63)/931,8 = 0,0248. Произведение индексной дельты одного опциона на его количество в портфеле дает индексную дельту позиции по данному контракту (последняя колонка таблицы). Так, индексная дельта позиции по контракту VLO 22,5 колл равна Di = −400 × 0,0248 = −9,93. Суммирование индексных дельт всех позиций (то есть всех значений, приведенных в последней колонке таблицы) дает индексную дельту портфеля, соответствующую формуле (3.2.3). В данном примере DPortfolio = −0,61. Используя формулу (3.2.4), это значение легко преобразуется в процентную индексную дельту: 

Анализ эффективности использования индексной дельты для оценки риска
Для исследования эффективности индексной дельты нами проведены статистические исследования на исторической базе данных, содержащей восьмилетнюю историю цен опционов и их базовых активов. В качестве базовых активов были задействованы акции, составляющие индекс S&P 500.
На историческом горизонте с начала 2001 г. по начало 2009 г. для каждой даты экспирации была сформирована серия портфелей. Момент создания каждого портфеля отстоял от даты экспирации на разное количество торговых дней. Так, самый «дальний» из портфелей был удален от даты истечения на 60 дней, следующий за ним – на 59 дней и так далее вплоть до последнего портфеля, отстоящего от момента экспирации всего на два дня. Таким образом, на каждую дату экспирации было создано 59 портфелей, отличающихся друг от друга продолжительностью времени, остающегося до дня истечения опционов. Всего было создано от 30 (для 60 дней) до 90 (для двух дней) портфелей для каждого «количества дней до экспирации».
Каждый портфель состоял из коротких стрэддлов для всех акций, входящих в состав указанного индекса. Страйк стрэддлов выбирался по принципу наименьшей удаленности от текущей цены БА. Объем позиции по каждому стрэддлу вычислялся как округленная до лотов (1 лот = 100 опционов) величина N = 10 000/U, где U – цена акции, являющейся БА для данного стрэддла. Бета каждой акции вычислялась по 120-дневной выборке доходностей акции и индекса. Дельты опционов Δi рассчитывались по модели Блэка – Шоулса; процентные индексные дельты D%Portfolio – по формуле (3.2.4). Кроме того, для каждого портфеля вычислялись следующие величины:
• Процентное изменение индекса I% = 100 × (Ie – It)/It, где It – значение индекса на момент t создания портфеля, Ie – значение индекса на момент истечения опционов.
• Процентное изменение стоимости портфеля P%realized = 100 × (Pe − Pt)/Pt где Pt – рыночная стоимость портфеля на момент t создания портфеля, Pe – стоимость портфеля на момент истечения опционов (премии опционов брались в середине спреда цены спроса и предложения). Этот показатель выражает «реализовавшийся» риск портфеля.
• Ожидаемое процентное изменение стоимости портфеля P%expected = 100 × (I%× D%Portfolio)/Pt. Этот показатель выражает оценку риска сложноструктурированного портфеля при условии, что индекс изменится на заданную величину (в данном исследовании – на величину реально произошедшего движения рынка).
• Разность реализовавшегося изменения стоимости портфеля и ожидаемого изменения стоимости портфеля Difference = P%realized – P%expected. Чем ближе к нулю этот показатель (то есть чем меньше абсолютное отклонение реализовавшегося изменения от ожидаемого), тем точнее индексная дельта позволяет прогнозировать будущие колебания стоимости портфеля.
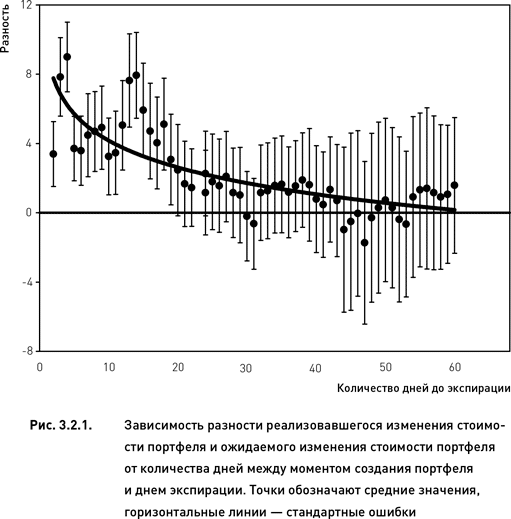
На рис. 3.2.1 показаны средние отклонения реально произошедших изменений стоимости портфеля от ожидаемых значений. Для портфелей, созданных в период от 30 до 60 дней до экспирации, средняя разность оказалась близка к нулю. Однако этим же портфелям свойственна и наибольшая изменчивость разности (представленная на рис. 3.2.1 в виде стандартных ошибок). Обратная картина наблюдается для портфелей, созданных незадолго до экспирации (от двух до 20 дней). В этих случаях разности реализовавшегося и ожидаемого изменений стоимости портфеля велики и положительны, хотя достаточно стабильны (стандартные ошибки невелики).
Положительные значения разности говорят о том, что P%realized > P%expected (реализовавшиеся изменения стоимости портфеля больше, чем ожидалось). Это означает, что оценка риска с помощью индексной дельты для этих портфелей была заниженной, то есть риск оказался недооценен (поскольку убыток коротких портфелей возникает в тех случаях, когда их стоимость возрастает (P%realized > 0)). Соответственно, отрицательное значение разности означает, что реальные изменения стоимости портфеля оказались меньше, чем ожидалось (то есть риск был переоценен). Поскольку стандартные ошибки портфелей, созданных задолго до экспирации, далеко заходят как в отрицательную, так и в положительную область (рис. 3.2.1), можно заключить, что многие из них были переоценены и многие – недооценены.
В целом можно сделать вывод, что в момент создания портфеля чем больше срок до даты истечения опционов, тем более точно (в среднем) оценивается риск. Вместе с тем вероятность ошибочных оценок также возрастает. Для портфелей, создаваемых вблизи экспирации, оценка риска оказывается заниженной, однако величина занижения является достаточно стабильной (вероятность ошибки мала). В первом случае можно добиться повышения эффективности использования индексной дельты путем введения дополнительных показателей риска. Во втором случае, поскольку изменчивость результатов невелика, можно ограничиться введением поправочных коэффициентов.
Известно, что дельта является локальной величиной, оценивающей изменение стоимости опциона при небольшом изменении цены его базового актива. Это означает, что чем больше реально произошедшее изменение цены базового актива, тем менее точен прогноз изменения стоимости опциона, основанный на дельте. Исследуем, справедливо ли данное утверждение для индексной дельты и насколько ухудшается эффективность ее прогноза при больших изменениях индекса. Для этого рассмотрим зависимость разностей между реализовавшимися и ожидаемыми изменениями стоимости портфеля от процентного изменения индекса.
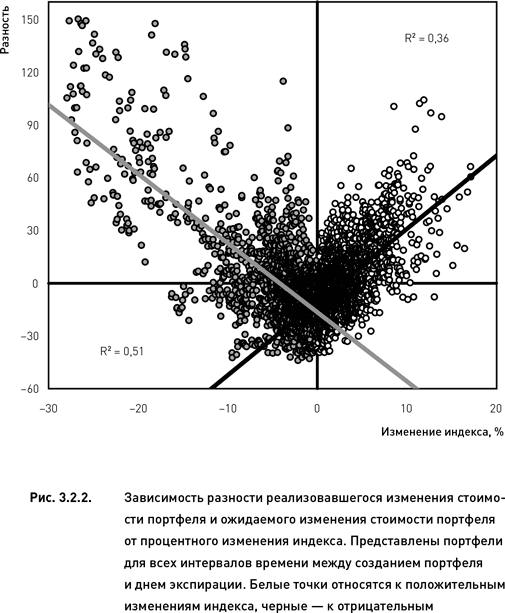
Из рис. 3.2.2 следует, что большие движения индекса действительно сопровождаются весьма серьезными отклонениями реальных изменений стоимости портфелей от прогнозных значений. Это наблюдение справедливо как для случаев роста индекса (белые точки на рис. 3.2.2), так и для случаев его падения (черные точки). Следует также отметить, что в тех случаях, когда индекс снижался, корреляция между разностью и изменением индекса была выше, чем когда индекс рос.
Для оценки эффективности индексной дельты наибольший интерес представляет тот факт, что большим движениям индекса (будь то рост или падение) соответствуют только положительные разности, в то время как малым – в основном отрицательные (рис. 3.2.2). Это говорит о том, что при больших движениях рынка индексная дельта недооценивает риск, а при малых – переоценивает. В тех же случаях, когда амплитуда колебаний рынка находится в пределах 3–5 % (в сторону роста или понижения), индексная дельта демонстрирует наибольшую эффективность.
В предыдущем исследовании мы ограничились случаями, когда риск оценивается только один раз – в момент создания портфеля. Эффективность этой оценки тестировалась также единожды – на дату истечения входящих в состав портфеля опционов (предполагается, что все опционы истекают одновременно). Теперь мы исследуем ситуации, когда риск оценивается регулярно в течение всего периода существования портфеля, а эффективность оценки тестируется на разных временных интервалах.
Мы будем оценивать эффективность индексной дельты так же, как в предыдущем исследовании (путем сравнения оценки риска, выраженного через индексную дельту, со значениями, реализовавшимися на практике). Чтобы проанализировать качество прогноза на разных этапах существования портфеля, следует (1) вычислять значения индексной дельты каждый день на протяжении всего инвестиционного периода и (2) оценивать изменения стоимости портфеля в течение разных периодов времени (будем называть их горизонтами тестирования или прогнозирования). Необходимо протестировать все периоды от первого дня до максимально возможного (49 дней в нашем исследовании). Эти данные позволят всесторонне оценить расхождения между прогнозами и реальностью.
Для каждой даты экспирации был сформирован портфель, состоящий из коротких стрэддлов для всех 500 акций, входящих в S&P 500. Момент создания каждого портфеля отстоял от даты истечения формирующих его опционов на 50 торговых дней. Всего было создано 90 таких портфелей. Страйк стрэддлов выбирался по принципу наименьшей удаленности от текущей цены базового актива. Объем позиции по каждому стрэддлу рассчитывался как округленная до лотов (1 лот = 100 опционов) величина, где U – цена акции, являющейся базовым активом для данного стрэддла.
В таблице 3.2.2 представлен пример такого портфеля и показана эволюция его показателей. В момент создания портфеля (7 августа 2008 г., первая строка таблицы) оставалось 50 рабочих дней до даты экспирации опционов (17 октября 2008 г.). Во второй строке таблицы приведены характеристики этого же портфеля на следующий день после его создания, в третьей строке – на третий день и т. д. вплоть до экспирации (в целях экономии места в таблице 3.2.2 показаны только первые 20 дней существования портфеля).
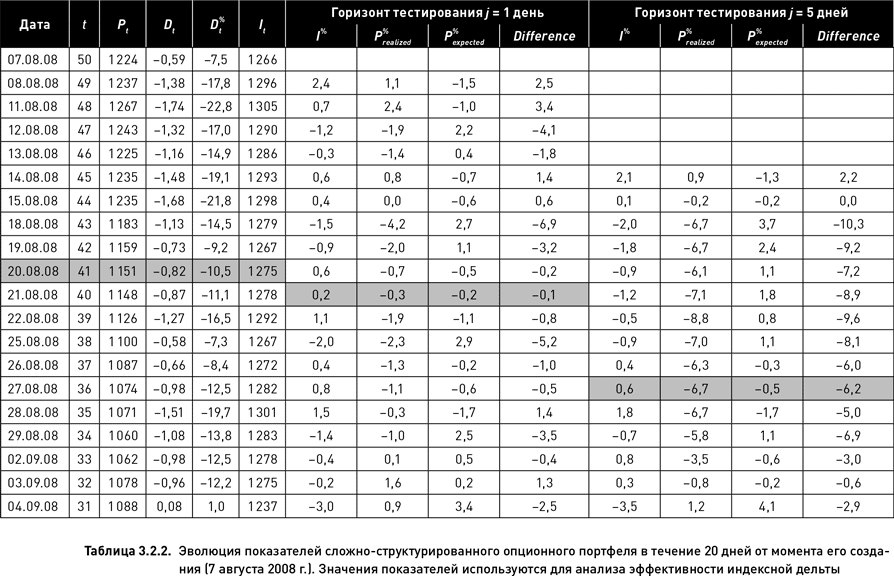
В таблице приводятся значения следующих показателей, необходимых для оценки разности между прогнозным и реализовавшимся значением риска.
• Количество дней, остающихся до экспирации t (используется для индексирования моментов оценки и тестирования).
• Рыночная стоимость портфеля Pi на момент оценки t; вычисляется как сумма стоимостей всех входящих в состав портфеля опционов.
• Индексная дельта Di, рассчитанная на момент t с помощью формулы (3.2.1).
• Процентная индексная дельта D%t = It Dt / 100, рассчитанная на момент t; прогнозирует изменение стоимости портфеля при изменении индекса на 1 %.
• Значение индекса It на момент оценки t и процентное изменение индекса I% = 100(It−j − It) / It − где It−j – значение индекса на момент тестирования; j выражает количество дней между двумя датами t и t-j и является горизонтом тестирования.
• Процентное изменение стоимости портфеля P%realized = 100(Pt−j − Pt) / Pt, где Pt – рыночная стоимость портфеля на момент оценки t, Pt−j – стоимость портфеля на момент тестирования. Этот показатель выражает изменение стоимости портфеля, произошедшее в течении j дней, и является, по сути, риском портфеля, реализовавшимся на определенном горизонте тестирования. Напомним, что рост стоимости опционов короткого портфеля (то есть положительное изменение его стоимости) приносит убыток, а снижение их стоимости дает прибыль.
• Ожидаемое процентное изменение стоимости портфеля P%expected = 100 I%D%Portfolio / Pt. Этот показатель выражает оценку риска сложноструктурированного портфеля при условии, что в течении j дней индекс изменится на величину I%.
• Разность реализовавшегося изменения стоимости портфеля Difference = P%realized − P%expected и ожидаемого изменения стоимости портфеля. Положительные значения разности указывают на недооценку риска индексной дельтой; отрицательные разности свидетельствуют о переоценке риска. Соответственно, чем ближе к нулю этот показатель, тем точнее индексная дельта позволяет прогнозировать будущие колебания стоимости портфеля.
В таблице 3.2.2 приведены расчеты для двух горизонтов тестирования – один и пять дней. Возьмем для примера 41-й день до экспирации (t = 41, выделено серым цветом в таблице) и проделаем поэтапно все вычисления, необходимые для оценки разности между прогнозируемым и реализовавшимся риском. Индексная дельта в этот день оценки равна:

Для горизонта тестирования j = 1 процентное изменение индекса составляет:

Процентное изменение стоимости портфеля равно:

а ожидаемое процентное изменение стоимости портфеля составляет:
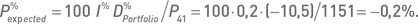
Разность реализовавшегося и ожидаемого изменений стоимости портфеля равна:

что указывает на небольшую переоцененность риска в данном случае. Для горизонта тестирования j = 5 процентное изменение индекса составило:

Изменение стоимости портфеля равно:

а ожидаемое процентное изменение стоимости портфеля оказалось равным:

Разность реализовавшегося и ожидаемого изменений стоимости портфеля в этом случае была намного большей и составила:

что указывает на существенную переоцененность риска. Аналогичным образом были рассчитаны все 90 портфелей. Риск каждого из них оценивался ежедневно в течение всех 50 дней существования портфеля. Эффективность этих оценок тестировалась на всех горизонтах от одного до 49 дней.
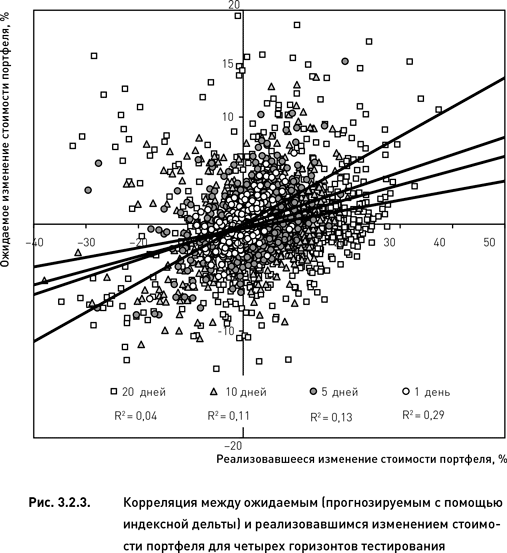
Взаимозависимость показателей прогнозируемого и реализовавшегося риска дает наглядное представление о степени эффективности индексной дельты. Рис. 3.2.3 демонстрирует такую зависимость для начального этапа существования портфелей (с 50-го по 40-й день до экспирации). Наибольшая корреляция обнаружена для однодневного горизонта тестирования. В этом случае «размытость» облака точек оказалась наименьшей (коэффициент корреляции R² = 0,29 наибольший). Удлинение горизонта тестирования до 5, 10 и 20 дней привело к постепенной деградации качества прогноза. Визуальный анализ рис. 3.2.3 показывает, что чем больше был горизонт тестирования, тем слабее становилась зависимость между прогнозом и результатом вплоть до полного исчезновения всякой зависимости (для 20 дней R² = 0,04). Кроме того, увеличение горизонта тестирования сопровождалось уменьшением угла наклона соответствующей регрессии. Это также свидетельствует об ухудшении прогнозных качеств индексной дельты на больших горизонтах тестирования.
Регрессионный анализ, представленный на рис. 3.2.3, является наиболее простым и интуитивно понятным средством качественной оценки индексной дельты. Вместе с тем он не дает строгого количественного выражения эффективности этого индикатора риска. Для этих целей лучше подходит средняя разность реализовавшихся и ожидаемых изменений стоимости портфеля. Поскольку убыток коротких портфелей возникает в тех случаях, когда их стоимость возрастает P%realized > 0, положительные разности (P%realized > P%expected) свидетельствуют о том, что оценка риска с помощью индексной дельты занижена (то есть риск недооценен). Соответственно, отрицательные разности означают, что реальные изменения стоимости портфеля меньше ожидавшихся (то есть риск переоценен).
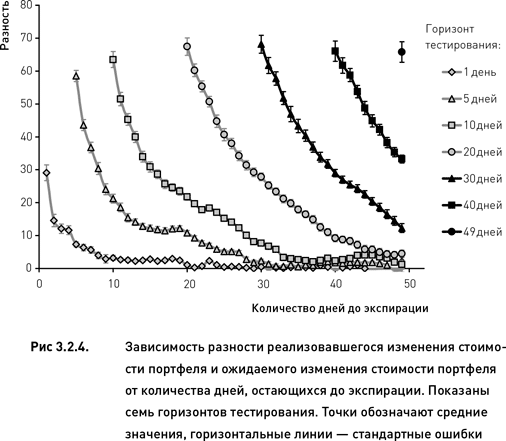
На рис. 3.2.4 показаны средние разности и стандартные ошибки (выражающие меру изменчивости результатов) для разных горизонтов тестирования. Для наиболее эффективного однодневного горизонта тестирования отклонения реально произошедших изменений стоимости портфелей от прогнозных значений были близки к нулю на всем периоде от создания портфелей до приблизительно 20-го дня до экспирации. После 20-го дня чем ближе портфель приближался к дате экспирации, тем более недооцененным оказывался риск. Таким образом, индексная дельта позволяет достаточно точно прогнозировать риск, но на весьма короткий промежуток времени (один день) и только на раннем и среднем этапах существования портфеля (в течение 30 рабочих дней с момента его формирования). Пятидневный горизонт тестирования дал похожие результаты, с той разницей, что в этом случае недооценка риска начала возникать уже с 30-го дня до экспирации и достигла более высоких значений. Дальнейшее увеличение горизонта тестирования способствовало еще большему усилению этих тенденций – недооценка риска начиналась раньше и достигала больших значений (рис. 3.2.4). Кроме того, легко заметить, что для коротких горизонтов тестирования зависимость между разностью и количеством дней до экспирации является нелинейной. В то же время для больших горизонтов тестирования эта зависимость постепенно становится линейной и все более «крутой». В данном случае крутизна наклона линии регрессии характеризует скорость деградации прогноза по мере приближения даты истечения опционов.
Полную информацию об эффективности индексной дельты и характере ее зависимости от двух исследуемых параметров (момента оценки и горизонта тестирования) дает представление данных в виде топографической карты. В двумерной системе координат будем откладывать по горизонтальной оси количество дней, остающихся до экспирации, а по вертикальной – горизонт тестирования. С помощью разных оттенков изобразим изолинии, отражающие средние разности реализовавшихся и ожидаемых изменений стоимости портфелей. Топография такой поверхности показана на рис. 3.2.5. Легко заметить, что область высокой эффективности индексной дельты располагается в правом нижнем углу диаграммы (показана на рисунке пунктирной линией). В целом можно заключить, что (1) индексная дельта позволяет довольно точно оценивать риск в первые 25–30 дней с момента создания портфеля; (2) эффективность этих оценок сохраняется в течение 20–25 дней с момента оценки. Треугольная форма зоны высокой эффективности указывает на то, что, с одной стороны, по мере приближения экспирации необходимо снижать горизонт прогнозирования. С другой стороны, использование больших горизонтов прогнозирования возможно лишь на начальном этапе существования портфеля.
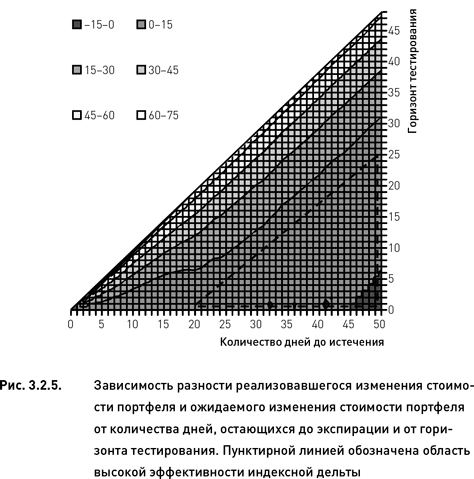
Применимость индексной дельты
Оценка риска сложно-структурированного опционного портфеля с помощью индексной дельты достаточно эффективна на ранних этапах существования портфеля, однако снижается по мере его «старения» и приближения даты экспирации. Являясь величиной локальной, индексная дельта способна качественно прогнозировать риск лишь на относительно короткие промежутки времени. Существует прямая зависимость между количеством дней, остающихся до экспирации, и горизонтом прогнозирования – чем ближе экспирация, тем короче должны быть горизонты прогнозирования. В противном случае риск может оказаться существенно недооценен.
Поскольку все результаты, полученные в настоящем исследовании, были достаточно стабильны (имели низкую стандартную ошибку, см. рис. 3.2.4), проблема недооценки риска может решаться путем введения поправочных коэффициентов. Значения коэффициентов можно получать методом построения диаграммы, аналогичной представленной на рис. 3.2.5. Необходимо лишь оптимизировать глубину исторического периода и правильно подобрать значения других параметров, используемых при построении диаграммы.
3.2.3. Коэффициент асимметрии
Этот показатель выражает меру асимметричности платежной функции портфеля относительно определенного индекса (например, S&P 500). Основная идея состоит в том, что большинство стратегий, связанных с продажей непокрытых опционов, базируется на принципе маркет-нейтральности. Если портфель действительно нейтрален по отношению к рынку, то его платежная функция будет симметричной – это означает, что как при росте, так и при падении рынка стоимость портфеля будет изменяться приблизительно одинаково (разумеется, при равных величинах роста и падения). Если же нейтральность нарушена, то платежная функция будет смещенной относительно текущего значения индекса, а коэффициент асимметричности будет выражать меру этого смещения.
Поскольку стоимость портфеля P равна сумме стоимостей входящих в его состав опционов, то зависимость стоимости портфеля от изменений индекса I можно выразить суммой:
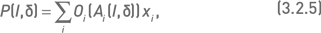
где Oi – стоимость i-го опциона, δ – относительное изменение индекса (например, δ = 0,12 означает, что индекс вырос или упал на 12 %), другие символы имеют тот же смысл, что и в предыдущих разделах. Зависимость Ai от I × δ и можно выразить с помощью беты βi, которая представляет собой коэффициент линейной регрессии доходностей базового актива и доходностей индекса. Зная бету, можно приблизительно определить стоимость базового актива при условии, что индекс изменится на заданную величину:

Используя модель Блэка−Шоулза, можно вычислить стоимости всех входящих в портфель опционов при условии, что цены их базовых активов равны значениям, рассчитанным по формуле 3.2.6. Суммируя полученные значения, получаем стоимость портфеля, соответствующую формуле 3.2.5. Нам необходимо рассчитать две стоимости портфеля – для случая роста индекса на величину I × δ и для случая его падения на такую же величину. Обозначим эти стоимости P(Ai(I,δ)) и P(Ai(I, − δ)) соответственно. Имея эти значения, можем рассчитать коэффициент асимметрии портфеля по следующей формуле:
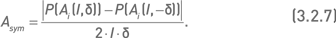
Если построить график платежной функции портфеля, отложив по оси X значения индекса, а по оси Y стоимость портфеля, то Asym можно представить как модуль коэффициента наклона прямой, соединяющей две точки графика с абсциссами X = I(1 + δ) и X = I(1 − δ). Чем больше величина коэффициента отклоняется от нуля, тем более асимметрична платежная функция (если коэффициент равен нулю, то платежная функция портфеля полностью симметрична).
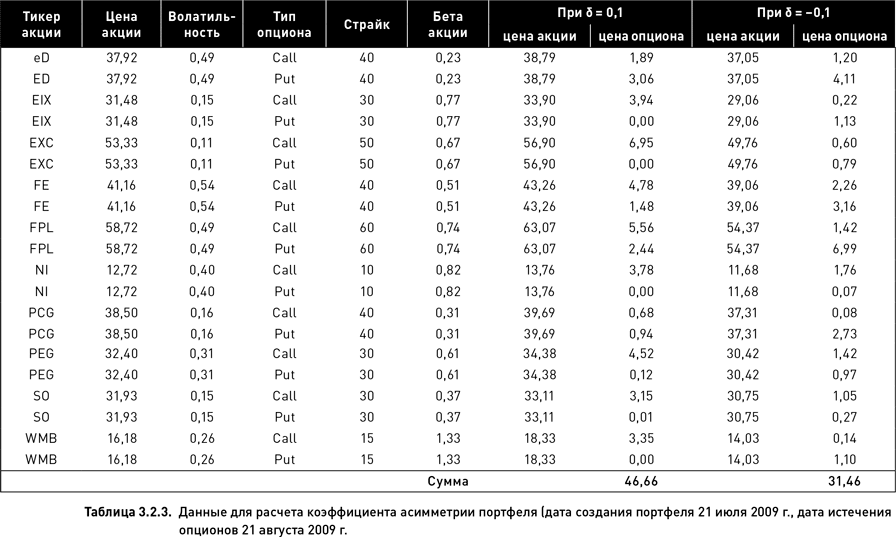
В таблице 3.2.3 приведены данные, необходимые для расчета коэффициента асимметрии портфеля, состоящего из 10 коротких стрэддлов (для простоты предположим, что количество каждого опциона в портфеле равно единице xi = 1). Например, цена акции ED при β = 0,23 и росте индекса на 10 % (δ = 0,1) будет равна 37,92(1 + 0,23 × 0,1) = $38,79. Подставляя это значение в формулу Блэка−Шоулза вместо текущей цены акции, находим, что стоимость опциона колл равна $1,89, а стоимость пут $3,06. Определив таким образом стоимости всех опционов, суммируем их и находим, что в случае роста индекса стоимость портфеля составит $46,66, а в случае падения – $31,46. Подставляя эти данные в формулу 3.2.7 и учитывая, что значение индекса S&P 500 на дату создания портфеля было 954,58, находим:

3.2.4. Вероятность убытка
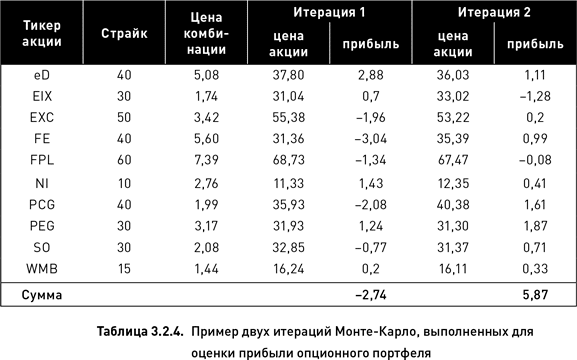
Вероятность того, что на дату истечения опционов портфель окажется убыточным, рассчитывается методом Монте-Карло. Для каждого опциона в портфеле производится генерация случайной цены его базового актива на определенный момент времени в будущем (для простоты мы будем генерировать цены на дату экспирации). Далее вычисляются прибыли и убытки опционов для полученных цен акций. Сумма полученных значений дает оценку прибыли/убытка портфеля. Описанный цикл представляет собой одну итерацию. Многократно повторяя итерации для одного и того же портфеля, можно получить достоверную оценку многих его характеристик.
В таблице 3.2.4 приведен пример двух итераций для портфеля, использованного ранее в таблице 3.2.3. Цены акций генерировались, используя логнормальное распределение с волатильностью, равной исторической волатильности, рассчитанной на периоде 120 торговых дней. При моделировании учитывались взаимные корреляции цен акций, рассчитанные на том же историческом периоде. Первая итерация для акции EIX сгенерировала цену $31,04, что подразумевает прибыль в размере $0,70 (30 + 1,74 – 31,04), зато вторая итерация для этой же акции дала убыток в размере $1,28. Для портфеля в целом первая итерация оказалась убыточной, а вторая – прибыльной (таблица 3.2.4).
Полный набор итераций для одного портфеля называется симуляцией (в своих расчетах мы использовали 20 000 итераций для каждой симуляции). Отношение числа убыточных итераций к общему числу итераций в симуляции дает оценку вероятности убытка портфеля. Например, если из 20 000 итераций 7420 были убыточными, то вероятность того, что данный портфель действительно окажется убыточным, составляет 0,37.

