Рубеж первый: игральная кость
1
Непредсказуемое и предопределенное проявляются одновременно, делая все таким, как есть. Так природа создает себя, в любых масштабах, от снежинки до бурана. Это такое счастье. Снова быть в самом начале, снова не знать почти ничего.Том Стоппард. Аркадия
На столе передо мной лежит одна красная игральная кость. Эта кость осталась у меня после поездки в Лас-Вегас. Я влюбился в нее сразу, как увидел ее на столе для игры в крэпс. Ее конструкция – само совершенство. Идеально прямые ребра, сходящиеся в точку на углах кубика. Грани такие гладкие, что на ощупь не определить, какому числу соответствует та или иная грань. Очки вырезаны на гранях кости и заполнены краской, имеющей ту же плотность, что и пластмасса, из которой сделана сама кость. Поэтому сторона, соответствующая шестерке, нисколько не легче, чем противоположная ей грань с одним очком. Кость невероятно приятно держать в руке. Очень красивая вещь.
И все-таки я ее ненавижу.
Сейчас ко мне обращена грань с тремя очками. Но, если я возьму кость и брошу ее, я никак не могу узнать, какой стороной она упадет. Она – абсолютный символ непознаваемого. Кажется, что будущее кости может быть известно, только когда оно становится прошлым.
Меня всегда чрезвычайно раздражали вещи, которых я не могу узнать. То, чего я не в силах постичь. Я ничего не имею против незнания каких-то вещей, если существует возможность в конце концов вычислить, что происходит. При наличии достаточного времени. Неужели эта кость действительно непознаваема? Или же, имея достаточную информацию, я мог бы предсказать ее следующее положение? Наверняка нужно всего лишь применить правильные законы физики и решить соответствующие математические уравнения. Наверняка это можно узнать.
Наука, в которой я работаю, математика, была придумана, чтобы дать человеку возможность увидеть, что его ожидает. Чтобы заглянуть в будущее. Чтобы стать хозяином, а не слугой судьбы. Я верю в то, что Вселенная работает в соответствии с некими законами. Если я пойму эти законы, я смогу познать Вселенную. Способность замечать закономерности дала роду человеческому чрезвычайно мощное средство управления жизнью. Существование закономерности означает, что у нас есть шанс предсказать будущее и познать непознаваемое. Закономерность движения Солнца означает, что мы можем быть уверены, что завтра оно снова взойдет, а Луна снова станет полной через 28 восходов Солнца. Именно так и появилась математика. Математика – наука закономерностей. Способность замечать закономерности – это мощное оружие в эволюционной борьбе за выживание. Наскальные рисунки в пещерах Ласко показывают, что, если отсчитать 13 четвертей луны от первого зимнего восхода Плеяд, получишь то время года, в которое лошади ходят жерёбые и на них легко охотиться. Способность предсказывать будущее – это ключ к выживанию.
Но существуют и такие вещи, которые, по-видимому, не имеют закономерностей или же имеют закономерности слишком сложные или скрытые для постижения человеческим разумом. Единичный бросок игральной кости не похож на восход Солнца. Кажется, что никак невозможно узнать, какая из шести граней кубика будет обращена вверх, когда он наконец остановится. Поэтому еще со времен античности кости использовали для разрешения споров и игр, в том числе и на деньги.
Неужели этот красивый красный кубик с белыми точками в самом деле непознаваем? Во всяком случае, сложные отношения с динамикой этого кубика возникли далеко не у меня первого.
Познать волю богов
Во время недавней поездки в Израиль я повез своих детей на археологические раскопки в Бейт-Гуврин. В древности это поселение было настолько популярным, что раскоп состоит из множества слоев разных городов, построенных друг поверх друга. В земле лежит столько всего, что археологи с радостью позволяют дилетантам – вроде нас с детьми – помогать им в раскопках, даже если в результате несколько горшков и оказываются разбиты. Мы конечно же раскопали множество осколков керамики. Но кроме того, мы все время вынимали из земли многочисленные кости животных. Мы думали, что это были остатки от трапезы, но наш экскурсовод объяснил, что на самом деле таким был самый древний вид игральных костей.
Археологические раскопки поселений начиная со времени неолита обнаруживают среди осколков посуды и кремней, которые обычно находят в местах обитания человека, непропорционально большое количество пяточных костей овец или других животных. Эти кости не что иное, как предки моей кости из казино. Если бросить такую кость, она естественным образом падает на одну из четырех сторон. На костях часто бывают вырезаны буквы или цифры. Предполагается, что такие ранние кости использовались не столько для азартных игр, сколько для гадания. И эта связь между результатом броска кости и волей богов просуществовала многие столетия. Люди верили, что знание того, как упадет кость, находится за пределами человеческого разумения. Результат броска определялся волей Божьей.
Постепенно такие кости занимали все более прозаичное место элемента мира развлечений. Первые кости кубической формы, похожие на кость с моего стола, были найдены в районе Хараппы, в современном Северо-Восточном Пакистане, где еще в 3-м тысячелетии до н. э. возникла одна из первых урбанистических цивилизаций. В это же время появляется игральная кость в форме четырехгранной пирамиды, найденная в городе Ур в Древней Месопотамии.
Играми в кости увлекались и римляне, и греки, и средневековые воины, которые привезли из Крестовых походов новую игру под названием «хэзард», происходящим от арабского названия игральной кости – аль-зар. Эта игра была ранним вариантом игры в крэпс, в которую играют в казино Лас-Вегаса, откуда я и привез свою кость.
Если бы падение костей можно было предсказать, никакие основанные на них игры не прижились бы. Интерес игры в нарды, в хэзард или в крэпс как раз и вытекает из незнания того, как упадут кости. Так что, возможно, игроки не оценят моих попыток предсказать результаты броска костей.
Многие века никто даже не думал, что такое свершение возможно. Древние греки, одними из первых создавшие математику в качестве средства ориентации в окружающем их мире, уж точно не имели никакого представления о том, как подойти к такой динамической задаче. Их математика, сводившаяся к жесткому, статичному миру геометрии, была неспособна справиться с игральной костью, катящейся по полу. Они смогли создать формулы, описывающие геометрические контуры куба, но движение кости было для них безнадежной задачей.
А как насчет опытов, которые позволили бы составить представление о возможных исходах броска? Антиэмпирическая позиция древних греков приводила к тому, что они не видели смысла в анализе данных и попытках научного предсказания падения кости. Ведь то, как упала уже брошенная кость, никак не влияет на результат следующего броска. Он случаен, что, с точки зрения древних греков, значило, что он непознаваем.
Аристотель считал, что происходящие в мире события по сути можно разделить на три категории: «неизбежные события», происходящие по необходимости в соответствии с законами природы, «вероятные события», происходящие в большинстве случаев, но с возможными исключениями, и, наконец, «непознаваемые события», происходящие по чистой случайности. Мою игральную кость Аристотель не колеблясь относит к последней категории.
По мере того как на философию оказывала влияние христианская теология, положение все ухудшалось. Поскольку исход броска кости находится во власти Бога, человек не смеет надеяться его познать. Как сформулировал блаженный Августин: «Мы называем те причины, которые считают случайными, не несуществующими, но скрытыми и приписываем их воле истинного Бога».
Случайности не существовало. Не существовало и свободы воли. Непознаваемое было известно Богу, который определял исход броска кости. Любая попытка предсказания такого исхода была делом еретиков, тех, кто осмеливался считать, что может познать мысли Бога. Французский король Людовик XI дошел до того, что запретил производство игральных костей, так как считал азартные игры богопротивными. Тем не менее кости – вроде той, что лежит у меня на столе, – в конце концов начали раскрывать свои тайны. Только в XVI в. игральные кости удалось вырвать из рук Божьих и передать их судьбу в руки – и в умы – человечества.
Поиск чисел в костях
Я кладу рядом со своей прекрасной костью из Лас-Вегаса еще две игральные кости. Спрашивается, если бросить все три кости сразу, что будет выгоднее: ставить на то, что выпадет 9 или 10? До XVI в. никаких средств, помогающих ответить на этот вопрос, не существовало. И все же любой достаточно много игравший сказал бы, что при броске только двух костей разумнее ставить на 9, чем на 10. В конце концов опыт игры вскоре подсказывает, что количество случаев, в которых выпадает 9, в среднем на треть больше, чем число таких, в которых выпадает 10. Но в случае трех костей почувствовать, как лучше ставить, сложнее, поскольку кажется, что 9 и 10 выпадают с равной частотой. Так ли это на самом деле?
Существование закономерностей, которые можно выгодно использовать в игре в кости, первым осознал в начале XVI в. в Италии один заядлый игрок по имени Джироламо Кардано. Эти закономерности нельзя было использовать в единичном броске. Они возникали в длинных сериях бросков, и игрок, подобный Кардано, который проводил за игрой в кости многие часы, мог бы извлечь из таких закономерностей некоторую выгоду. Он был настолько захвачен погоней за предсказаниями непознаваемого, что однажды даже продал имущество своей жены, только чтобы добыть денег на игру.
Кардано пришла в голову удачная мысль подсчитать число возможных вариантов выпадения костей. В случае броска двух костей таких вариантов 36. Они изображены на следующей схеме.
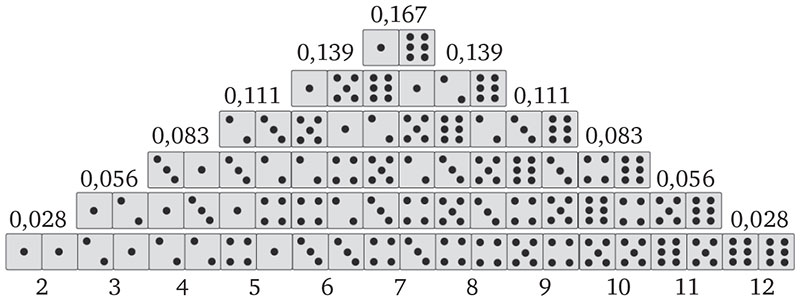
Только в трех из них сумма очков равна 10, а 9 можно получить в четырех вариантах. Поэтому Кардано рассудил, что, когда играют двумя костями, разумнее ставить на 9, чем на 10. Это не помогало в одной отдельно взятой игре, но в длинной серии игр Кардано мог выиграть, если бы придерживался результатов своих расчетов. К сожалению, строгость его математических рассуждений не сопровождалась такой же строгостью его поведения в игре. Он умудрился потерять все наследство, оставленное ему отцом, и даже вступал в поножовщину со своими соперниками, когда ему особенно не везло в кости.
Тем не менее он постарался добиться исполнения одного из своих пророчеств. По-видимому, он предсказал дату собственной смерти – 21 сентября 1576 г. Чтобы не оставлять исполнение этого предсказания на волю случая, он взял дело в собственные руки. Когда наступил предсказанный день, он совершил самоубийство. Мне, как бы я ни стремился к знаниям, это кажется некоторым перебором. Собственно говоря, большинство людей предпочло бы не знать дату собственной смерти. Но Кардано нужна была только победа, даже в игре в кости со смертью.
Перед самоубийством он написал книгу, которую многие считают первым шагом к пониманию поведения игральной кости, катящейся по столу. Хотя он написал свою «Книгу об играх случая» (Liber de Ludo Aleae) еще в 1564 г., этот труд долго оставался неизвестным и не был опубликован до 1663 г.
На самом деле не кто иной, как великий итальянский физик Галилео Галилей, использовал тот же анализ, который описал Кардано, чтобы выяснить, следует ли ставить на 9 или на 10, когда бросают три кости. Он рассудил, что существует 6 · 6 · 6 = 216 возможных исходов падения костей. Из них в 25 случаях выпадает 9, а в 27 случаях – 10. Разница невелика, и обнаружить ее эмпирическим путем было бы непросто, но и ее достаточно для того, чтобы в долгой игре было выгоднее ставить на 10.
Прерванная игра
Математическое освоение игры в кости переместилось из Италии во Францию в середине XVII в., когда два крупных игрока, Блез Паскаль и Пьер де Ферма, обратили свои мысли на предсказание будущего этих кувыркающихся кубиков. Проблема понимания исхода броска костей заинтересовала Паскаля после встречи с одним из величайших игроков того времени, кавалером де Мере. Де Мере предложил Паскалю разрешить несколько интересных ситуаций. Одна из них сводилась к задаче, решенной Галилеем. Однако в число других входил вопрос о том, разумно ли ставить на выпадение по меньшей мере одной шестерки в четырех бросках кости, а также ставшая впоследствии знаменитой «задача о ставках».
Паскаль завязал оживленную переписку с великим математиком и юристом Пьером де Ферма, вместе с которым они попытались решить задачи, поставленные де Мере. В случае броска четырех костей можно рассмотреть 6 · 6 · 6 · 6 = 1296 разных исходов и подсчитать, в скольких из них выпадает шестерка, но задача становится при этом довольно громоздкой.
Вместо этого Паскаль рассудил, что в одном броске шестерка не выпадет с вероятностью 5/6. Поскольку все броски независимы, вероятность того, что шестерка не выпадет ни в одном из четырех бросков, равна 5/6 · 5/6 · 5/6 · 5/6 = 625/1296 = 48,2 %. Что означает, что вероятность увидеть шестерку равна 51,8 %. Это чуть больше половины, значит, вполне есть смысл ставить на такой исход.
«Задача о ставках» была еще интереснее. Предположим, что два игрока – назовем их Паскаль и Ферма – бросают игральную кость. Ферма выигрывает партию, если на кости выпадает 4 или более очков; в противном случае эту партию выигрывает Паскаль. Таким образом, при каждом броске кости у каждого из них есть половинный шанс на выигрыш партии. Они поставили на кон 64 фунта, которые достанутся тому, кто первым выиграет три партии. Однако игру прерывают, и продолжить ее невозможно. К этому моменту Ферма выиграл две партии, а Паскаль – одну. Как следует разделить между ними 64 фунта?
Традиционные попытки решения этой задачи были сосредоточены на том, что произошло в прошлом. Может быть, раз Ферма выиграл в 2 раза больше партий, чем Паскаль, то и его выигрыш должен быть в 2 раза больше? Но, если, например, перед тем как игра была остановлена, Ферма выиграл всего одну партию, такое решение становится бессмысленным. Паскаль в таком случае не получает ничего, хотя по-прежнему имеет шанс на победу. Никколо Фонтана Тарталья, современник Кардано, после долгих размышлений пришел к выводу, что решения не существует: «Это вопрос скорее юридический, чем математический, и любой вариант разделения выигрыша может стать поводом для тяжбы».
Однако другие не были готовы признать свое поражение. Они обратили внимание не на прошлое, а на то, что могло бы случиться в будущем. В противоположность первой задаче здесь они попытались не предсказать, как ляжет кость, а представить все возможные варианты будущего и разделить выигрыш в соответствии с разными исходами, благоприятными для того или другого игрока.
Здесь легко впасть в заблуждение. Кажется, что существует три сценария. Если следующую партию выигрывает Ферма, он забирает себе все 64 фунта. Если следующую партию выигрывает Паскаль, то играется еще одна, финальная партия, которую может выиграть либо Паскаль, либо Ферма. Поскольку в двух из этих трех случаев выигрывает Ферма, то, видимо, ему причитаются две трети ставки. В эту-то ловушку и попал де Мере. Паскаль утверждает, что это решение ложно: «Кавалер де Мере – человек очень остроумный, но он вовсе не математик; это, как вы знаете, огромный недостаток». Вот уж действительно!
Паскаль же, напротив, был великий математик, и он считал, что выигрыш следует разделить иначе. Ферма может выиграть в следующей партии (и получить 64 фунта) с вероятностью 50 %. Но, если в следующей партии выиграет Паскаль, шансы обоих на победу в финальной партии равны, так что выигрыш можно разделить поровну – по 32 фунта каждому. Ферма в любом случае гарантированно получает 32 фунта. Поэтому оставшиеся 32 фунта следует разделить поровну, что в итоге дает Ферма 48 фунтов.
Ферма согласился с анализом Паскаля. «Я ясно вижу, что истина, будь она в Тулузе или в Париже, одна и та же», – писал ему в Тулузу Паскаль.
Пари паскаля
Анализ ставок в игре, разработанный Паскалем и Ферма, можно применить и к гораздо более сложным ситуациям. Паскаль выяснил, что тайна распределения выигрыша сокрыта внутри того, что теперь называют треугольником Паскаля.
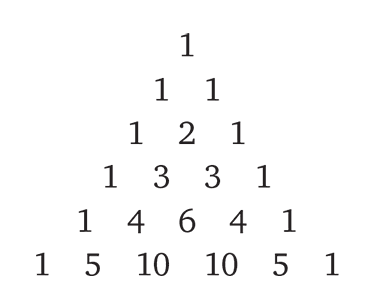
Треугольник устроен таким образом, что каждое число в нем равно сумме двух чисел, расположенных непосредственно над ним. Полученные числа определяют, как следует разделить выигрыш в любой прерванной игре. Например, если Ферма до победы не хватает двух выигранных партий, а Паскалю – четырех, нужно взять строку треугольника номер 2 + 4 = 6 и найти сумму первых четырех чисел и сумму последних двух. Эти суммы дают пропорцию, в которой следует разделить выигрыш. В данном случае получается пропорция 1 + 5 + 10 + 10 = 26 к 1 + 5 = 6. Таким образом, Ферма получает 26/32 · 64 = 52 фунта, а Паскаль – 6/32 · 64 = 12 фунтов. В общем случае решение для игры, в которой Ферма не хватает n, а Паскалю – m выигранных партий, можно найти в (n + m) – й строке треугольника Паскаля.
Есть данные, что французы опоздали с открытием связи между этим треугольником и исходом азартных игр на несколько тысячелетий. Игральные кости и другие методы получения случайных результатов, например «И цзин», издавна использовали в Китае в попытках предсказать будущее. В тексте книги «И цзин», созданном около 3000 лет назад, для случайного выбора гексаграммы, значение которой затем можно истолковать, используется в точности та же таблица, которую Паскаль составил для анализа исходов подбрасывания монет. Однако создателем треугольника считают в наше время Паскаля, а не китайцев.
Паскаль интересовался не только игральными костями. Он предпринял знаменитую попытку приложения своей новой вероятностной математики к величайшему из неизвестных – существованию Бога.
Бог есть или Бога нет. Но на которую сторону мы склонимся? Разум тут ничего решить не может. Нас разделяет бесконечный хаос. На краю этого бесконечного расстояния разыгрывается игра, исход которой неизвестен. […] На чем же вы остановитесь? Так как выбор сделать необходимо, то посмотрим, что представляет для вас меньше интереса: вы можете проиграть две вещи, истину и благо, и две вещи вам приходится ставить на карту, ваши разум и волю, ваше познание и ваше блаженство; природа же ваша должна избегать двух вещей: ошибки и бедствия. Раз выбирать необходимо, то ваш разум не потерпит ущерба ни при том, ни при другом выборе. Это бесспорно; ну а ваше блаженство? Взвесим выигрыш и проигрыш, ставя на то, что Бог есть. Возьмем два случая: если выиграете, вы выиграете все; если проиграете, то не потеряете ничего. Поэтому не колеблясь ставьте на то, что Он есть.
В этом рассуждении, известном под названием «пари Паскаля», он утверждает, что выбор веры в Бога приносит гораздо больший выигрыш. Если такой выбор ошибочен, вы ничего не теряете; если он справедлив, вы выигрываете вечную жизнь. И вместе с тем ставка на то, что Бога нет, в случае проигрыша приносит вечное проклятие, а в случае выигрыша не дает ничего, кроме знания, что Бога действительно нет. Этот аргумент рассыпается, если вероятность существования Бога на самом деле равна нулю, но, даже если это и не так, цена верования может оказаться слишком высокой по сравнению с вероятностью существования Бога.
Вероятностные методы, разработанные математиками, подобными Ферма и Паскалю, для разрешения неопределенности, оказались невероятно могущественными. Явления, считавшиеся недоступными для познания, выражением воли богов, начали становиться досягаемыми для человеческого разума. На сегодня такие вероятностные подходы являются лучшим из имеющихся у нас средств исследования буквально всего, от поведения частиц газа до подъемов и падений рынка ценных бумаг. Действительно, кажется, что сама природа материи отдана на милость математической вероятности, как мы увидим на «Рубеже третьем», говоря об использовании квантовой физики для предсказания поведения наблюдаемых нами частиц. Но с точки зрения поисков определенности такие вероятностные методы представляют собой раздражающий компромисс.
Я, безусловно, ценю величайшие открытия, сделанные Ферма, Паскалем и другими, но они не помогают мне узнать заранее, сколько очков выпадет на брошенной мной кости. Сколько я ни изучал математическую теорию вероятностей, меня никогда не покидало чувство неудовлетворенности. Единственное, что вбивает в голову любой курс теории вероятностей, – это идея о том, что, сколько бы раз подряд у вас ни выпадала шестерка, это никак не влияет на поведение кости при следующем броске.
Так можно ли как-нибудь узнать, как упадет моя кость? Или же это знание навечно останется недоступным? Не останется, если верить откровениям одного ученого, жившего за морем, в Англии.
Математика природы
Для меня Исаак Ньютон – главный герой борьбы с непознаваемым. Идея о том, что я могу узнать о Вселенной все, происходит из революционной работы Ньютона «Математические начала натуральной философии». Эта книга, впервые изданная в 1687 г., посвящена разработке нового математического языка, обещавшего дать инструменты, которые откроют секреты устройства Вселенной. В ней была предложена разительно новая модель занятий наукой. Как заявил в 1747 г. французский физик Алексис Клеро, эта работа «пролила свет математики на науку, которая до тех пор оставалась во тьме догадок и гипотез».
Она также была попыткой объединения, создания теории, которая описывала бы небесное и земное, великое и малое. Кеплер предложил законы, описывающие движение планет, которые он разработал эмпирически, опираясь на данные и пытаясь найти уравнения, которые воссоздавали бы прошлое. Галилей описал траекторию шара, летящего в воздухе. Гениальность Ньютона позволила ему понять, что эти два примера – проявления одного и того же феномена: гравитации.
Ньютон, появившийся на свет на Рождество 1643 г. в городе Вулсторп в Линкольншире, всегда стремился обуздать физический мир. Он делал механические и солнечные часы, строил миниатюрные мельницы на мышиной тяге, чертил бесчисленные планы зданий и кораблей и делал подробные зарисовки животных. Жившая в его доме кошка однажды исчезла, улетев на сделанном Ньютоном воздушном шаре. Однако отзывы его школьных учителей не сулили ему блестящего будущего: его называли «невнимательным и ленивым».
Надо сказать, что лень может быть не самым плохим качеством для математика. Она может быть мощным стимулом для изобретательного поиска какого-нибудь легкого способа решения задачи, избавляющего от упорной и монотонной работы. Но учителя, как правило, не ценят это качество.
И действительно, Ньютон так плохо учился в школе, что мать сочла его учебу пустой тратой времени и решила, что ему будет полезнее научиться управлять семейной фермой в Вулсторпе. К сожалению, в деле управления хозяйством Ньютон оказался столь же безнадежным, так что его снова отправили в школу. Хотя эта история наверняка апокрифична, говорят, что внезапное превращение Ньютона в ученого совпало с ударом по голове, который он получил от школьного хулигана. Как бы то ни было, после этого преображения Ньютон внезапно стал блестящим учеником и в конце концов поступил на учебу в Тринити-колледж в Кембридже.
В 1665 г., когда в Англии вспыхнула эпидемия бубонной чумы, Кембриджский университет был из предосторожности закрыт. Ньютон вернулся домой, в Вулсторп. Изоляция часто бывает важным ингредиентом изобретения новых идей. Ньютон запирался в своей комнате и размышлял.
Истина – дитя тишины и размышлений. Я постоянно держал предмет своих размышлений перед собой и ждал, пока первые проблески медленно, мало-помалу не разгорятся, превращаясь в яркий и ясный свет.
Будучи изолирован в Линкольншире, Ньютон создал новый язык, способный выразить картину постоянно изменяющегося мира, – язык математического анализа. Этому инструменту предстояло стать ключом к возможности заблаговременного знания о будущем поведении Вселенной. Именно этот язык дает мне надежду узнать, какой стороной может упасть моя игральная кость.
Математические фотографии
Математический анализ пытается разобраться в математической задаче, которая на первый взгляд кажется бессмысленной: деление ноля на ноль. Когда я роняю свою игральную кость на стол, именно эту задачу мне нужно решить, чтобы узнать мгновенную скорость кости, летящей в воздухе.
Скорость кости постоянно увеличивается, поскольку сила тяжести тянет ее к земле. Как же вычислить, чему равна эта скорость в любой момент времени? Например, с какой скоростью падает кость через одну секунду? Скорость равна пройденному расстоянию, деленному на прошедшее время. Значит, я могу измерить расстояние, которое она пролетит в течение следующей секунды, и получить среднюю скорость за этот период. Но я хочу узнать точную скорость. Я могу измерить расстояние, пройденное за более краткий промежуток времени, скажем, за половину или четверть секунды. Чем меньше длительность такого интервала, тем точнее я могу вычислить скорость. В конце концов для получения точного значения скорости я буду вынужден взять бесконечно малый временной интервал. Но тогда мне придется вычислять результат деления ноля на ноль.
Придуманное Ньютоном исчисление сделало такой расчет возможным. Он понял, как можно вычислить то значение, к которому скорость стремится по мере уменьшения длительности временного отрезка. Этот революционный новый язык смог выразить картину постоянно изменяющегося мира. Геометрия древних греков была совершенным средством для описания статической, застывшей картины мира.
Математический анализ: осмысление деления ноля на ноль
Рассмотрим автомобиль, начинающий движение из неподвижного состояния. В момент включения секундомера водитель нажимает на педаль газа. Предположим, что, согласно нашим измерениям, в течение t секунд водитель проехал t · t м. С какой скоростью машина будет ехать через 10 секунд? Мы можем получить приблизительное значение скорости, измерив расстояние, пройденное автомобилем между 10-й и 11-й секундами. Средняя скорость за эту секунду равна (11 · 11–10 · 10)/1 = 21 м/с.
Но, взяв среднюю скорость на меньшем временном отрезке, скажем, длительностью 0,5 секунды, мы получим:
(10,5 · 10,5 – 10 · 10)/0,5 = 20,5 м/с.
Это, конечно, чуть медленнее, так как автомобиль разгоняется и во вторую половину секунды, которая прошла между 10-й и 11-й, он в среднем едет быстрее. Возьмем теперь еще меньший промежуток. Давайте еще раз разделим его пополам:
(10,25 · 10,25–10 · 10)/0,25 = 20,25 м/с.
Я надеюсь, что ваш внутренний математик уже заметил закономерность. Если взять временной промежуток длительностью х секунд, то средняя скорость за это время будет равна 20 + x м/с. По мере того как мы рассматриваем все меньшие интервалы, она все более приближается к 20 м/с. Так что, хотя кажется, что определение скорости на 10-й секунде требует вычисления частного 0/0, математический анализ позволяет понять, что это означает.
Великое математическое открытие Ньютона дало нам язык, способный описать мир движущийся. Математика перешла от описания натюрморта к воспроизведению движущегося изображения. В науке произошло нечто подобное случившемуся в этот же период перевороту в искусстве, когда динамическое искусство барокко вырвалось из статического искусства Возрождения.
Вспоминая это время, которое он называл «annus mirabilis», Ньютон считал его одним из самых продуктивных периодов своей жизни. «Я был в расцвете сил и думал о Математике и Философии больше, чем когда-либо после».
Все, что нас окружает, находится в состоянии постоянного изменения, поэтому неудивительно, что эти математические методы приобрели такое большое влияние. Но, с точки зрения Ньютона, математический анализ был инструментом для личного пользования, позволившим ему получить научные выводы, изложенные в «Началах», великом труде, изданном в 1687 г., в котором он описывал свои идеи о гравитации и законах движения.
Говоря о себе в третьем лице, он объясняет, что его математический анализ был ключом к открытиям, содержащимся в этой книге: «Г-н Ньютон открыл большую часть предложений, изложенных в его “Началах”, при помощи этого нового Анализа». Но никакого описания этого «нового анализа» опубликовано не было. Вместо этого Ньютон частным образом распространял свои идеи среди друзей, но не испытывал никакого желания представить их на суд общественности.
К счастью, теперь этот язык широко доступен, и я лично потратил несколько лет на его изучение, когда учился математике. Но мои попытки познания игральной кости требуют использования математического открытия Ньютона в сочетании с его великим вкладом в физику – знаменитыми законами движения, которыми открываются его «Начала».
Правила игры
Ньютон излагает в «Началах» три простых закона, на которых в огромной степени основывается динамика Вселенной.
Первый закон движения Ньютона: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».
Это было не так уж и очевидно, например, Аристотелю. Если покатить шар по плоской поверхности, то через некоторое время он остановится. Кажется, что для продолжения его движения необходимо приложить силу. На самом же деле существует скрытая сила, изменяющая скорость шара, – сила трения. Если нашу игральную кость бросить где-нибудь в космосе, вдали от гравитационных полей, она так и будет лететь по прямой линии с постоянной скоростью.
Для изменения скорости или направления движения объекта требуется сила. Второй закон Ньютона объяснял, как именно такая сила изменяет движение, и содержал в себе новый инструмент, созданный для выражения этого изменения. Математический анализ уже позволил мне выразить скорость кости по мере ускорения ее падения к столу. Скорость изменения этой скорости также можно узнать при помощи анализа. Второй закон Ньютона утверждает, что между силой, прилагаемой к объекту, и изменением его скорости существует прямая связь.
Второй закон движения Ньютона: «Скорость изменения движения, или ускорение, пропорциональна приложенной к телу силе и обратно пропорциональна его массе».
Чтобы понять движение таких тел, как падающая игральная кость, необходимо понять, какие силы могут на них воздействовать. Закон всемирного тяготения Ньютона выявил одну из основных сил, оказывающих влияние, скажем, на падающее яблоко или на планеты, движущиеся в Солнечной системе. Этот закон гласит, что сила, действующая на тело массой m1 со стороны тела массой m2, равна
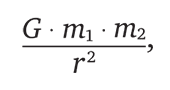
где G – эмпирическая физическая постоянная, определяющая силу гравитации в нашей Вселенной.
При помощи этих законов теперь можно описать траекторию шара, падающего в воздухе, или планеты, движущейся в Солнечной системе, или же игральной кости, падающей из руки игрока. Но, когда кость падает на стол, возникает следующая проблема. Что происходит в этот момент? Подсказку дает третий закон движения Ньютона: «Когда одно тело прилагает силу к другому, второе тело одновременно прилагает к первому силу, равную ей по величине и противоположную по направлению».
Сам Ньютон получил при помощи этих законов необыкновенный набор результатов, касающихся Солнечной системы. Он писал: «Остается изложить, исходя из тех же начал, учение о строении системы мира». Он начал приложение своих идей к траекториям планет с того, что представил каждую планету в виде точки, расположенной в ее центре масс, и предположил, что вся масса планеты сосредоточена в этой точке. Затем, используя свои законы движения и свой новый математический аппарат, он смог вывести законы планетарного движения Кеплера.
Ему также удалось рассчитать соотношения масс крупных планет, Земли и Солнца. Он объяснил несколько интересных отклонений в движении Луны, приписав их притяжению Солнца. Он также заключил, что форма Земли не соответствует идеальной сфере, но должна быть сплюснута у полюсов благодаря вращению Земли, порождающему центробежную силу. Французы придерживались противоположной точки зрения: они считали, что Земля должна быть вытянута на полюсах. В 1733 г. была отправлена экспедиция, которая подтвердила правоту Ньютона – и могущество математики.
Ньютонова «теория всего»
Это было необычайное достижение. Три закона стали теми зернами, из которых можно было вывести движение всех частиц Вселенной. Они по праву заслуживали названия «теории всего». Я называю их «зернами», потому что труд других ученых потребовался, чтобы взрастить их и применить к более сложным задачам, чем ньютоновская Солнечная система, состоящая из точечных масс. Например, в своем изначальном виде законы движения были непригодны для описания движения менее жестких или деформируемых тел. Уравнения, обобщающие законы Ньютона, предложил великий швейцарский математик XVIII в. Леонард Эйлер. Уравнения Эйлера можно было применять к более общим случаям, например к колеблющейся струне или к качающемуся маятнику.
Появлялось все больше и больше уравнений, управляющих разными природными явлениями. Эйлер создал уравнения для невязких жидкостей. Французский математик Жозеф Фурье получил в начале XIX в. уравнения, описывающие тепловой поток. Его соотечественники Пьер-Симон Лаплас и Симеон-Дени Пуассон использовали уравнения Ньютона для создания более общих уравнений гравитации, которые, как потом выяснилось, управляют также и другими явлениями, например гидродинамикой и электростатикой. Поведение вязких жидкостей было описано уравнениями Навье – Стокса, а электромагнитные явления – уравнениями Максвелла.
Казалось, что открытием математического анализа и законов движения Ньютон превратил Вселенную в детерминистическую машину с часовым механизмом, управляемую математическими уравнениями. Ученые полагали, что они действительно открыли «теорию всего». Вот как выразил веру большинства ученых в необычайное могущество математики, позволяющее ей рассказать все о физическом мире, математик Пьер-Симон Лаплас в опубликованных в 1814 г. «Опытах философии теории вероятностей»:
Мы должны рассматривать настоящее состояние Вселенной как следствие ее предыдущего состояния и как причину последующего. Ум, которому были бы известны для какого-либо данного момента все силы, одушевляющие природу, и относительное положение всех ее составных частей, если бы вдобавок он оказался достаточно обширным, чтобы подчинить эти данные анализу, обнял бы в одной формуле движения величайших тел Вселенной наравне с движениями мельчайших атомов: не осталось бы ничего, что было бы для него недостоверно, и будущее, так же как и прошедшее, предстало бы перед его взором.
В столетия, последовавшие за великим произведением Ньютона, мнение о теоретической познаваемости Вселенной, как прошлой, так и настоящей, стало преобладающим среди ученых. Казалось, что всякая мысль о Боге, действующем в мире, совершенно исчезла. Бог, возможно, сыграл свою роль в запуске механизмов Вселенной, но начиная с этого момента его место заняли уравнения математики и физики.
Так как же насчет нашей прозаической игральной кости? Уж наверное, имея в своем распоряжении законы движения, можно будет предсказать исход броска на основе простого сочетания геометрии кубика, начального направления его движения и последующего взаимодействия с поверхностью стола? Я выписал все эти уравнения в свой блокнот, и они выглядят довольно-таки устрашающе.
Ньютон также обдумывал задачу предсказания поведения костей. Его интерес к ней был вызван письмом, которое он получил от Сэмюэла Пипса. Пипс просил Ньютона посоветовать, на что ему следует поставить в пари, которое он собирался заключить со своим другом:
1) что при броске шести костей выпадет хотя бы одна шестерка,
2) что при броске двенадцати костей выпадут по меньшей мере две шестерки или
3) что при броске восемнадцати костей выпадут по меньшей мере три шестерки.
Пипс собирался поставить 10 фунтов (что эквивалентно 1000 фунтов в сегодняшних деньгах) и был бы очень рад получить хороший совет. Интуиция Пипса подсказывала ему, что наиболее вероятен третий вариант, но Ньютон ответил, что с точки зрения математики должно быть справедливо обратное. Ставить следует на первый вариант. Однако для решения этой задачи Ньютон обратился не к своему математическому анализу и законам движения, а к идеям, разработанным Ферма и Паскалем.
Но, даже если бы Ньютон и смог решить выписанные мною уравнения, описывающие траекторию игральной кости, обнаружилась бы еще одна проблема, способная уничтожить всякую надежду на познание будущего моей кости. Хотя Паскаль и говорил о своем пари с Богом, в его анализе есть одна интересная строка, сильно затрудняющая любые попытки познания будущего: «Разум тут ничего решить не может. Нас разделяет бесконечный хаос».
Судьба Солнечной системы
Если Ньютон – мой герой, то французский математик Анри Пуанкаре в моей истории о предсказании будущего должен быть злодеем. И все же я не могу винить его за то, что он нанес один из самых сокрушительных ударов всем желающим узнать, что произойдет дальше. Он и сам был не особенно рад своему открытию с учетом того, что оно обошлось ему весьма недешево.
Пуанкаре, родившийся столетием позже Лапласа, разделял веру своего соотечественника во Вселенную, устроенную наподобие часового механизма, управляемую математическими законами и совершенно предсказуемую. «Если бы мы точно знали законы природы и положение Вселенной в начальный момент, мы могли бы точно предсказать положение той же Вселенной в последующий момент».
Понимание устройства мира было, с точки зрения Пуанкаре, главным стимулом занятий математикой. «В математике фактами, заслуживающими изучения, являются те, которые ввиду их сходства с другими фактами способны привести нас к открытию физического закона».
Хотя законы движения Ньютона породили целый массив математических уравнений, описывающих эволюцию физического мира, большинство таких уравнений все еще чрезвычайно сложно было решить. Возьмем уравнения состояния газа. Газ можно считать состоящим из молекул, сталкивающихся друг с другом как мельчайшие бильярдные шары, и будущее поведение газа теоретически подчиняется законам движения Ньютона. Но само количество таких шариков означает, что любое точное решение этой задачи недостижимо. Статистические или вероятностные методы по-прежнему оставались значительно лучшим средством понимания поведения миллиардов молекул.
Однако в одном случае число бильярдных шаров было достаточно малым, и решение задачи представлялось достижимым. Речь идет о Солнечной системе. Пуанкаре был одержим вопросами предсказания судьбы планет, кружащихся навстречу своему будущему.
Гравитационное притяжение между одной планетой и другой, находящейся на некотором расстоянии от первой, такое же, как если бы вся масса планеты была сосредоточена в ее центре тяжести, и потому для определения судьбы, ожидающей Солнечную систему, планеты можно считать точками в пространстве, как делал Ньютон. Это значит, что для описания эволюции Солнечной системы достаточно трех координат, определяющих положение центра масс каждой из планет в пространстве, и еще трех чисел, соответствующих их скорости по каждому из трех пространственных направлений. Сила, воздействующая на каждую планету, определяется гравитационными силами, действующими со стороны всех остальных планет. При наличии всей этой информации остается только применить второй закон Ньютона, чтобы проложить курс этих планет в самое отдаленное будущее.
Единственная проблема состоит в том, что математическое решение все равно остается чрезвычайно сложным. Ньютон решил задачу поведения двух планет (или планеты и Солнца). Они движутся по эллиптическим траекториям, причем общий фокус таких эллипсов расположен в их общем центре тяжести. Это движение повторяется периодически до скончания времен. Однако, попытавшись ввести в задачу третью планету, Ньютон зашел в тупик. Казалось бы, расчет поведения Солнечной системы, состоящей, скажем, из Солнца, Земли и Луны, должен быть достаточно простым, но в нем приходится решать уравнение с 18 переменными: 9 переменными положений (координатами) и 9 составляющими скоростей всех этих небесных тел. Ньютон признавал, что «одновременное рассмотрение всех причин движения и определение такого движения точными законами, допускающими несложные расчеты, превосходит, если я не ошибаюсь, возможности любого человеческого разума».
Разрешение этой проблемы получило новый толчок, когда король Швеции и Норвегии Оскар II решил предложить в честь своего шестидесятилетия премию за решение одной из еще нерешенных математических задач. На свете не так много монархов, которые отмечали бы свои юбилеи математическими задачами, но Оскар интересовался математикой еще с тех пор, когда он сам блистал в этой области, будучи студентом университета в Упсале.
Его величество Оскар II, желая дать новое подтверждение своего интереса к успехам математической науки, решил выдать 21 января 1889 г. награду за важное открытие в области высшего математического анализа. Награда состоит из золотой медали с изображением Его Величества стоимостью в тысячу франков и премии в две тысячи пятьсот крон.
Была создана комиссия из трех выдающихся математиков, которые должны были выбрать несколько подходящих математических проблем и оценить работы претендентов. Одно из предложенных ими заданий состояло в представлении математического доказательства устойчивости Солнечной системы. Будет ли она и дальше работать как часы, или же в какой-то момент в будущем Земля может улететь в пространство и покинуть пределы Солнечной системы?
Чтобы ответить на этот вопрос, необходимо было решить те самые уравнения, которые завели в тупик Ньютона. Пуанкаре полагал, что его мастерства должно быть достаточно для победы в конкурсе. Математики часто используют следующий прием: они пытаются сначала решить задачу в упрощенном варианте, чтобы понять, имеет ли она решение. Поэтому Пуанкаре начал с задачи трех тел. Но, поскольку и она была слишком сложной, он решил еще более упростить задачу. Вместо того чтобы рассматривать Солнце, Землю и Луну, почему бы не попытаться разобраться с системой, состоящей из двух планет и пылинки? Так как пылинка не будет влиять на планеты, можно предположить, что они будут попросту вращаться одна вокруг другой по эллиптическим траекториям в соответствии с решением Ньютона. И в то же время сама пылинка будет испытывать воздействие гравитационных сил обеих планет. Пуанкаре взялся за воссоздание траектории, описываемой такой пылинкой. Некоторое понимание этой траектории внесло бы интересный вклад в решение исходной задачи.
Хотя ему и не удалось полностью решить задачу, представленной им работы было более чем достаточно для получения премии короля Оскара. Пуанкаре смог доказать существование интересного класса траекторий, воспроизводящих самих себя, так называемых периодических траекторий. Периодические орбиты устойчивы по определению, так как они снова и снова повторяются во времени, подобно эллипсам, которые заведомо описывают две планеты системы.
Французские власти были чрезвычайно обрадованы тем, что награду получил их соотечественник. В XIX в. Германия опередила Францию по части математики, так что французские академики немедленно провозгласили победу Пуанкаре доказательством возрождения французской математики. Гастон Дарбу, непременный секретарь Французской академии наук, заявил:
Начиная с этого момента имя Анри Пуанкаре стало известно широкой публике, которая привыкла затем видеть в нашем коллеге не просто особенно многообещающего математика, но великого ученого, которым Франция по праву может гордиться.
Маленькая ошибка и ее большие последствия
Решение Пуанкаре готовилось к изданию в специальном выпуске журнала Acta Mathematica Шведской королевской академии наук. И тут наступил тот самый момент, которого больше всего на свете боится каждый математик. Худший кошмар любого математика. Пуанкаре думал, что его работе ничто не угрожает. Он проверил каждый шаг своего доказательства. И перед самой публикацией один из редакторов журнала усомнился в одном из этапов математического рассуждения.
Пуанкаре считал, что малые изменения положения планет, небольшие округления в некоторых местах, были допустимы, так как они могли вызвать лишь малые изменения предсказанных орбит. Это предположение казалось вполне разумным. Но никакого обоснования этому допущению приведено не было. А в математическом доказательстве каждый шаг, каждое предположение должны быть основаны на строгой математической логике.
Редактор попросил Пуанкаре как-либо объяснить этот пробел в доказательстве. Но, когда Пуанкаре попытался обосновать этот шаг, он осознал, что допустил серьезную ошибку. Пытаясь ограничить ущерб для своей репутации, он написал председателю комитета по присуждению премии Гёсте Миттаг-Леффлеру:
Последствия этой ошибки серьезнее, чем я предполагал вначале. Не скрою от Вас, насколько огорчило меня это открытие […]. Не знаю, признаете ли Вы оставшиеся результаты достойными той высокой награды, которую Вы им присудили. (Во всяком случае, я могу лишь признаться Вам как верному другу в своем замешательстве.) Я напишу Вам подробнее, когда буду яснее понимать положение.
Миттаг-Леффлер решил известить других членов жюри:
Работа Пуанкаре обладает такой редкой глубиной и творческой силой, что она несомненно откроет новую эпоху в анализе и его приложениях к астрономии. Однако разъяснения необходимо значительно расширить, и в данный момент я прошу многоуважаемого автора просветить меня по некоторым важным вопросам.
Сражаясь с возникшей проблемой, Пуанкаре понял, что он попросту был неправ. Даже малое изменение начальных условий может привести к возникновению разительно отличающихся орбит. Предложенное им приближение было недопустимым. Его предположение было ошибочным.
Пуанкаре телеграфировал печальные новости Миттаг-Леффлеру и попытался остановить публикацию своей статьи. Он писал ему в смущении:
Может случиться, что малые различия в начальных условиях порождают чрезвычайно большие расхождения в результирующих явлениях. Малая ошибка в первых порождает огромную ошибку в последних. Предсказания становятся невозможными.
Это сообщение «чрезвычайно озадачило» Миттаг-Леффлера:
Не то чтобы я сомневался в том, что Ваша работа в любом случае будет воспринята большинством геометров как гениальное произведение и станет отправной точкой для всех дальнейших трудов по небесной механике. Не думайте поэтому, что я сожалею о присуждении Вам премии […] Но хуже всего то, что Ваше письмо пришло слишком поздно и статья уже была разослана.
На карту была поставлена репутация Миттаг-Леффлера, который не обнаружил ошибку до публичного присуждения премии Пуанкаре. Не так следовало бы отмечать юбилей монарха! «Пожалуйста, не говорите никому ни слова об этой прискорбной истории. Завтра я сообщу Вам все подробности».
Следующие несколько недель прошли в попытках изъять отпечатанные экземпляры статьи, не возбуждая ничьих подозрений. Миттаг-Леффлер предложил Пуанкаре оплатить печать исходного варианта. Пристыженный Пуанкаре согласился, хотя стоимость тиража составила более 3500 крон, то есть на тысячу больше той премии, которую он изначально завоевал.
В попытке исправить положение Пуанкаре попробовал разобраться со своей ошибкой, понять, где и почему он был неправ. В 1890 г. он написал вторую, расширенную статью, в которой объяснял свое предположение о возможности внезапного разлета, по-видимому, устойчивых систем вследствие чрезвычайно малых изменений.
Открытие Пуанкаре, вызванное его ошибкой, привело к появлению одной из важнейших математических концепций прошлого века – понятия хаоса. Это открытие установило существенные пределы тому, что может познать человечество. Пусть я выписал все уравнения движения игральной кости, но что, если моя кость ведет себя подобно планетам Солнечной системы? В соответствии с открытием Пуанкаре, даже одна маленькая ошибка в определении начального положения кости может разрастись в огромное расхождение исхода броска к тому моменту, как кость закончит свое движение по столу. Значит ли это, что будущее игральной кости из Лас-Вегаса сокрыто завесой математики хаоса?
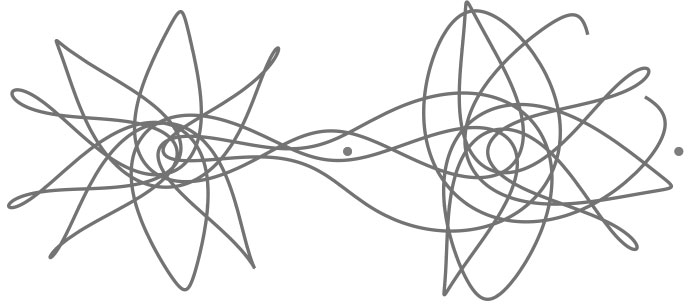
Хаотическая траектория единичной планеты, вращающейся вокруг двух солнц
Назад: Запредельность
Дальше: 2

