Книга: О том, чего мы не можем знать. Путешествие к рубежам знаний
Назад: 13
Дальше: Выражение признательности
14
Меня ужасает вечное безмолвие этих бесконечных пространств!Блез Паскаль. Мысли
Как мы выяснили на четвертом «рубеже», в физической Вселенной, в которой мы живем, есть пределы, дальше которых мы не можем видеть, за которыми мы ничего не можем исследовать. Однако я посвятил всю свою жизнь исследованию не физической Вселенной, а доступной лишь разуму вселенной математических истин. В ней мне не нужны ни телескопы, ни микроскопы, ни космические корабли. У меня есть другие инструменты, достигающие пределов мира. Прежде всего это вопрос о том, способны ли конечные средства, заключенные в моей голове, познать бесконечность. Математика позволяет нам заглянуть далеко за барьеры, останавливающие наши исследования краев физической Вселенной. Не существует никакого самого большого числа. На любую попытку воздвигнуть предел во вселенной чисел я всегда могу ответить прибавлением еще одной единицы. И это простое действие прибавления единицы позволяет мне создавать в моем разуме бесконечные миры.
Но как много я могу знать о таких бесконечных мирах? Есть ли пределы, ограничивающие возможности исследования истин этой бесконечной вселенной чисел при помощи конечных нейронных средств? До XIX в. слово «бесконечный» было равнозначно слову «непознаваемый». И тем не менее человек исследовал бесконечное при помощи своего конечного разума с тех самых пор, когда древние греки изобрели черную магию математики.
Взгляд в бесконечность
Вот еще один из математических анекдотов, которые вылетели из наших рождественских хлопушек:
Учитель. Назовите самое большое число.
Ученик. Семьдесят три миллиона двенадцать.
Учитель. А как же семьдесят три миллиона тринадцать?
Ученик. Ну вот, я был почти прав!
Древние греки понимали, что числа никогда не кончаются, но это понимание еще не означало знания о существовании подлинной бесконечности. Аристотель проводил различие между бесконечностью потенциальной и бесконечностью актуальной. Потенциально существует возможность прибавления единицы к каждому следующему числу, но реальное достижение численной бесконечности невозможно. Тем не менее удивительно, как грекам удавалось исследовать такую потенциальную бесконечность посредством конечных логических рассуждений.
Например, одно из первых великих математических доказательств, содержащихся в «Началах» Евклида, представляет собой объяснение того факта, что в мире чисел имеется бесконечное число неделимых чисел, которые мы называем простыми. Это доказательство по сей день приводит меня в восхищенный трепет: сама мысль о том, что нечто, кажущееся извне бесконечным и неподатливым, тем не менее можно понять. Можно спросить: раз мы допускаем возможность бесконечности чисел вообще, что может быть такого уж необычного в доказательстве существования бесконечного количества простых чисел? В конце концов, в знании о существовании бесконечного количества четных чисел нет ничего удивительного, если уж мы признали, что числа продолжаются бесконечно. И все же это доказательство остается поразительным в связи с тем, что мы на самом деле не понимаем природы простых чисел. Доказательство демонстрирует, что множество простых чисел бесконечно, не имея возможности сказать, что именно они собой представляют. Возможно, вопрос о конечности или бесконечности физической Вселенной требует использования аналогичного подхода: нужен логический аргумент, из которого следовало бы, что Вселенная должна продолжаться бесконечно, хотя мы никогда не сможем физически этого увидеть. Несмотря на все достижения древних греков, вопрос бесконечности оставался проблемным на протяжении тысячелетий. Чаще всего бесконечность считали выражением того, что недоступно нашему пониманию. Фома Аквинский, христианский богослов и философ XIII в., писал:
Существование актуального бесконечного множества невозможно, ибо любое множество вещей, которое мы себе представляем, должно быть множеством некоего вида. К тому же множества вещей определяются числом вещей в них. Однако никакое число не бесконечно, ибо числа порождаются пересчетом множества единиц. Следовательно, никакое множество вещей не может ни быть актуально бесконечным по своей природе, ни случайно стать бесконечным.
Обсуждение бесконечности всегда было близко к проблемам богословия. В V в. христианский философ Августин Аврелий писал в своей наиболее знаменитой работе «О граде Божьем», что бесконечность должна быть оставлена исключительно для божественного разума. Он с презрением отзывался о тех, «которые говорят, что бесконечное не может быть понято даже божественным ведением»:
Что же касается другого их мнения, согласно которому бесконечное не может быть объято даже божественным ведением, то им остается дерзнуть утверждать, что Бог не знает всех чисел, и погрузиться, таким образом, и в эту бездну глубокого нечестия. […] Кто даже из самых безрассудных людей скажет это? […] Кто такие мы, людишки, дерзающие положить предел Его ведению?
Средневековый философ Орем, который обдумывал идею о том, что за небесным сводом, окружающим нашу Вселенную, может существовать бесконечное пространство, также умело обращался и с математическими бесконечностями. Именно он первым доказал тот удивительный факт, что если складывать дроби 1 + 1/2 + 1/3 + 1/4 + …, то можно получить сколь угодно большой результат. Ему также одному из первых пришла в голову идея о возможности сравнения размеров разных бесконечностей. В самом деле, если сравнить бесконечность всех чисел и бесконечность четных чисел, то каждому целому числу можно сопоставить его удвоенное значение. Однако, поскольку множество четных чисел, очевидно, является меньшим подмножеством множества всех чисел, Орем заключил, что сравнение бесконечностей – дело небезопасное.
Несколько веков многие считали, что рассуждения такого рода доказывают невозможность реального существования бесконечности. Английский священник и математик XIV в. Томас Брадвардин использовал похожую идею, чтобы доказать, что мир не вечен. Он рассуждал так: если мир вечен, то число женских душ и число всех душ должны быть бесконечными. Если они бесконечны, их можно соотнести друг с другом. Но тогда не останется места для мужских душ. Таким образом, предположение о бесконечности числа душ приводит к противоречию.
И несколько столетий спустя бесконечность все еще чрезвычайно сильно беспокоит математиков. Галилей столкнулся с затруднениями, похожими на проблемы Орема и Брадвардина, когда рассматривал число квадратов целых чисел. С одной стороны, чисел, которые не являются квадратами, явно больше, чем квадратов. Квадраты – 1, 4, 9, 16, 25, … – встречаются чем дальше, тем реже, и между каждыми следующими двумя квадратами располагается все большее количество неквадратов. Но, с другой стороны, разве каждое число не является квадратным корнем из некоего числа-квадрата? С этой точки зрения можно сказать, что каждому числу можно сопоставить (его) квадрат, откуда следует, что количество квадратов должно быть равно количеству всех чисел.
Галилея, как ранее Орема, это привело в замешательство. Как он писал в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки»,
[…] рассуждая нашим ограниченным разумом о бесконечном, мы приписываем последнему свойства, известные нам по вещам конечным и ограниченным. Между тем это неправильно, так как такие свойства, как большая или меньшая величина и равенство, неприменимы к бесконечному, относительно которого нельзя сказать, что одна бесконечность больше или меньше другой или равна ей.
Общеизвестный сейчас символ, представляющий бесконечность, появился вскоре после смерти Галилея. Символ ∞ впервые использовал в 1655 г. английский математик Джон Валлис. Он выбрал именно такую форму, чтобы выразить идею возможности бесконечного прохождения по кривой. В течение следующих двух веков математики вполне свыклись с идеей потенциальной бесконечности, но не с идеей бесконечности, действительно существующей, которая, казалось, порождала слишком много трудностей. Математик XIX в. Карл-Фридрих Гаусс писал своему коллеге Генриху-Христиану Шумахеру:
Прежде всего я возражаю против использования бесконечной величины как чего-то законченного, что ни в коем случае недопустимо в математике. Бесконечность – не более чем façon de parler.
Укрощение бесконечности
А затем, в конце XIX в., произошел интеллектуальный сдвиг. Благодаря работе конечного разума одного человека бесконечность вдруг оказалась достижимой. Для Георга Кантора бесконечность не была всего лишь манерой выражаться. Она была осязаемым математическим объектом:
Horror infiniti […] можно рассматривать как своего рода близорукость, которая лишает возможности видеть актуальное бесконечное, хотя последнее в своем высшем, абсолютном носителе создало и сохраняет нас, а в своих вторичных трансфинитных формах окружает нас со всех сторон и даже присуще самому нашему духу.
В конце XIX в. можно было бы ожидать разделения между учеными и религиозными деятелями. Однако Георг Кантор был и тем и другим и писал о том, как религия влияет на его математические идеи. Подобно Джордано Бруно, размышлявшему о бесконечной Вселенной, вера в Бога была для Кантора гипотезой, из которой он выводил необходимость существования бесконечности.
В одном доказательстве исходят из понятия Бога и умозаключают
прежде всего от высшего совершенства божественного существа к возможности сотворения Transfinitum ordinatum, а затем от его всеблагости и величия к необходимости фактически последовавшего сотворения Transfinitum.
Предложенный Кантором способ рассмотрения бесконечности происходит из некоторых идей, которые обдумывал Орем. Утверждать, что два множества имеют одинаковые размеры, – значит найти способ сопоставления элементов одного множества с элементами другого, при котором для каждого такого элемента имеется парный ему элемент другого множества.
Подход Кантора к бесконечности сводится к представлению математиков в виде племени, у которого есть названия для чисел 1, 2 и 3, а все числа, превосходящие этот предел, называются словом «много», что для этого племени и означает бесконечность. Если два племени, не имеющие названий для чисел, больших трех, встретятся, они тем не менее смогут сравнить свои размеры и узнать, какое из них больше. Для этого члены первого племени должны образовать пары с членами второго племени, и «много» того племени, в котором останутся члены, не нашедшие себе пары, и будет наибольшим. Если все члены обоих племен окажутся в парах, значит, «много» этих племен одинаковы.
Эта модель хорошо описывает математику животного царства: животные, вероятно, не имеют названий для чисел, но все же могут определить, какая из групп больше других. Развитие чувства размера – ключевой элемент выживания. Если одна группа животных встречает другую группу, им нужно быстро оценить, больше их собственная группа или меньше, чем та, с которой они столкнулись. Если их больше, они вступают в схватку, если меньше, они убегают. Но для такого сравнения не нужны названия чисел. Сопоставляя членов обеих групп попарно, можно понять, что та группа, в которой останутся члены без пары, и будет большей.
Используя идею попарного сопоставления, Кантор смог предложить способ определения численного равенства или неравенства двух бесконечных множеств. Например, возможно, хотелось бы сказать, что четных чисел существует вдвое меньше, чем всех чисел вообще. Однако Кантор показал, что, как и предполагал Орем, можно сопоставить эти два множества так, чтобы каждому числу нашлась пара. Например, число 1 попадает в пару с числом 2, 2 – с 4, 3 – с 6, а число n с числом 2n. Поэтому размеры обоих множеств одинаковы. Племя, на спинах членов которого написаны четные числа, сможет оказать сопротивление племени, члены которого пронумерованы всеми числами. Эти бесконечные множества имеют одинаковые размеры.
Это рассуждение похоже на те, которые предлагали Орем и Галилей, и тем не менее их обоих беспокоил тот факт, что с другой точки зрения четные числа или квадраты являются подмножеством всех чисел и, следовательно, должны в некотором смысле составлять меньшее множество. Кантор считал, что обнаружения одного способа установления попарного соответствия должно быть достаточно для вывода о равенстве размеров двух множеств. В случае конечных множеств, если для них не удается найти попарных соответствий, никакие перестановки или изменения порядка элементов этих множеств не позволят добиться точного соответствия. Однако в случае множеств бесконечных Кантор обнаружил, что изменение порядка элементов может помочь обнаружить новые способы образования пар, которые не оставят без пары ни одного элемента.
Ключевым, с точки зрения Кантора, моментом было то, что существование хотя бы одного возможного способа установления попарного соответствия между двумя множествами позволяет сказать, что их размеры равны. Могут существовать способы подбора пар, когда некоторые члены племен остаются без пары: например, если составить пары только из четных чисел обеих групп, останется бесконечное количество нечетных чисел. Но, по мнению Кантора, множество чисел может быть признано истинно бо́льшим, только если не существует никакой возможности подобрать пары всем членам множества без какого бы то ни было остатка.
Как, например, обстоит дело с множеством таких чисел, как дроби? Насколько велика эта бесконечность? Кантор придумал замечательный способ сравнения всех целых чисел со всеми дробями и доказательства равенства размеров их множеств. На первый взгляд это кажется невозможным: между любыми двумя целыми числами помещается бесконечное множество дробей. Но существует способ установления точного соответствия между всеми целыми числами и всеми дробями, который не оставляет вне этого соответствия ни одной дроби.
Он начинается с построения таблицы, содержащей все дроби. В этой таблице бесконечно много столбцов и строк. n-й столбец содержит все дроби 1/n, 2/n, 3/n, ….
Как же Кантору удалось составить пары из целых чисел и дробей этой таблицы? Для этого прежде всего нужно запустить в таблицу змею, проползающую дроби по диагонали, как показано на иллюстрации. Тогда целые числа можно поставить в пары с дробными, продвигаясь по пути такой змеи: 1 попадает в пару с 1/1, 2 – с 2/1, 3 – с 1/2, 4 – с 1/3. Например, число 9 образует пару с 2/3, девятой по счету дробью, которую мы встречаем на извивающемся пути змеи, пробирающейся сквозь таблицу дробей. Поскольку змея таким образом проползает через всю таблицу, каждой из дробей будет поставлено в соответствие некоторое целое число.
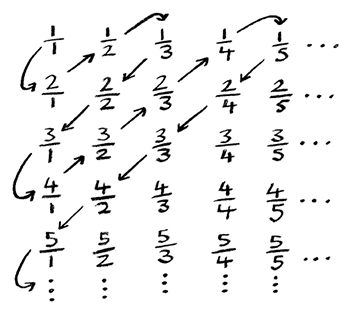
Это рассуждение красиво и неожиданно. Если бы я оказался на необитаемом острове и мог взять с собой всего восемь теорем, канторова змея была бы одной из них. Какое замечательное достижение – найти способ установления соответствия между всеми дробями и целыми числами и показать, что их множества имеют одни и те же порядки величины!
Несчетная бесконечность
Начинает казаться, что все бесконечности имеют равные размеры. Может быть, если число членов племени достигло бесконечности, никакое другое племя никогда не сможет его превзойти? Но тут появляется еще одно крутое племя, члены которого помечены всеми возможными десятичными представлениями положительных вещественных чисел. Сможет ли племя, члены которого помечены целыми числами 1, 2, 3, …, составить пары с членами этого нового племени? Для начала можно установить соответствие между членом племени с числом 1 и членом племени с числом π = 3,1415926…, затем между членом племени с числом 2 и членом племени с числом е = 2,71828…. Но как перебрать всех членов этого бесконечного десятичного племени? Есть ли какой-нибудь хитрый способ расположения бесконечных десятичных чисел, позволяющий целым числам проползти их все подобно тому, как Кантор сделал с дробями?
Кантор сумел придумать рассуждение, показывающее, почему, как бы мы ни пытались найти соответствие с племенем целых чисел, он всегда может гарантировать, что все члены племени бесконечных десятичных дробей никогда не будут пересчитаны. Бесконечность всех бесконечных десятичных представлений чисел – это бесконечность действительно более крупного вида, чем бесконечность целых чисел. Это рассуждение так же просто и красиво, и я думаю, что оно тоже вошло бы в число математических теорем, которые я взял бы с собой на необитаемый остров.
Как мог Кантор быть уверен, что он всегда сможет гарантировать существование члена племени бесконечных десятичных представлений, которому не найдется пары? Возьмем одну из моих попыток найти соответствия между племенем целых чисел и племенем бесконечных десятичных дробей.
13,1415926…
22,7182818…
31,4142135…
41,6180339…
50,3331779…
…
Кантор создает такое число в бесконечном десятичном представлении, которое заведомо не содержится в моем списке и не имеет пары среди целых чисел. В каждом десятичном разряде стоит цифра от 0 до 9. В качестве первого разряда Кантор берет цифру, отличающуюся от первого разряда числа, поставленного в пару числу 1. В качестве второго разряда – цифру, отличную от второго разряда числа, соответствующего числу 2.
13,1415926…
22,7182818…
31,4142135…
41,6180339…
50,3331779…
…
Например, бесконечное десятичное число 0,22518… не соответствует ни одному из первых пяти целых чисел, так как эта бесконечная десятичная дробь отличается от первых пяти бесконечных десятичных дробей в моем списке. Так Кантор может найти члена племени бесконечных десятичных чисел, которому не соответствует никакое целое число. Если я скажу, что ему соответствует, скажем, число 101, Кантор попросту ответит: «Проверьте 101-й разряд: он отличается от 101-го разряда этого нового числа».
В этом рассуждении есть некоторые технические тонкости. Например, следует избегать образования числа 0,9999…, поскольку, как мы помним по шутке про математиков и лампочку, оно на самом деле равно числу 1,000…. Но и краткого изложения доказательства достаточно, чтобы показать, что чисел с бесконечным десятичным представлением существует больше, чем целых чисел.
Можно возразить, что такое новое число можно просто добавить в список и сдвинуть все остальные числа на единицу. Но, сколько бы чисел мы ни добавили в список, Кантор всегда может повторить тот же фокус и изготовить еще одну бесконечную десятичную дробь, которой в списке нет. Суть в том, что это рассуждение применимо к любой попытке установления попарного соответствия между целыми числами и бесконечными десятичными дробями – лишние бесконечные десятичные дроби остаются всегда. Это несколько напоминает открытие Гёделя о том, что добавлением к математике недоказуемых истинных аксиом нельзя в конце концов добиться того, что все истинные утверждения станут доказуемы: всегда останутся «лишние» недоказуемые истины. Собственно говоря, Гёдель использовал для доказательства своей теоремы о неполноте прием, похожий на тот, что применил Кантор.
Сам Кантор был искренне удивлен своими открытиями, касающимися бесконечности. Он говорил: «Я это вижу, но я в это не верю».
Появление нескольких разных бесконечностей означало, что введенного Валлисом символа ∞ уже недостаточно. Более того, идеи Кантора доказали, что существует бесконечно много разных видов бесконечности. Кантор показал, что мы можем заменить слово «много» на более осмысленные названия всех этих разных бесконечностей. Он стал обозначать эти новые бесконечные числа новыми символами, в качестве которых он взял буквы еврейского алфавита. Самая меньшая бесконечность, א0, была названа «алеф-ноль» по первой букве еврейского алфавита. Кантор, вероятно, знал о ее мистическом значении в еврейской каббале, в которой она обозначает бесконечность Бога. Но для Кантора такой выбор символизировал еще и идею нового начала, отправной точки новой математики. Мне этот момент кажется одним из самых захватывающих в истории математики. Мы как бы впервые научились считать. Но вместо единиц – 1, 2, 3 – мы стали считать бесконечности.
Великий немецкий математик Давид Гильберт признавал, что Кантор создает действительно новую математику. Гильберт объявил, что идеи Кантора – это «самое удивительное произведение математической мысли, одно из наиболее прекрасных воплощений человеческой деятельности в области чистого разума […] Никто не сможет изгнать нас из рая, который создал для нас Кантор». Я, пожалуй, с ним согласен.
Кантор верил, что на самом деле его вдохновляет божественный разум. Он не создавал математику сам, а лишь пересказывал идеи, полученные от Бога. Может быть, именно вера в трансцендентное давала ему смелость поверить и в существование бесконечности. Но преобразование бесконечности из неизвестного в известное было произведено именно трудами математического гения самого Кантора. При этом христианская церковь, вовсе не смущаясь попытками Кантора заглянуть в бесконечное сознание Бога, проявляла живой интерес к возникающим у него идеям. Кантор вел длительную переписку о природе Бога и бесконечности с церковными деятелями.
Однако его идеи нравились не всем. В частности, один из самых влиятельных математиков Германии, Леопольд Кронекер, считал математику Кантора заблуждением, а его самого называл развратителем молодежи:
Не знаю, чего в теории Кантора больше, философии или теологии, но я уверен, что в ней нет математики.
Как известно, Кронекер однажды провозгласил: «Бог создал целые числа. Все остальное – дело рук человеческих». Но творение Кантора было столь революционно, что Кронекер считал его язвой на теле математики. Противодействие Кронекера канторовой бесконечности привело к тому, что Кантор так и не смог получить работы ни в одном из крупных университетов, включая Берлинский, в котором работал Кронекер. Вместо этого он провел всю свою жизнь в заштатном университете города Галле. Кантор пытался бороться и жаловался на поведение Кронекера самому министру просвещения. Но, судя по всему, враждовать с одним из виднейших членов математического сообщества было не самой удачной идеей.
Даже напечатать свои идеи ему было непросто. Другой влиятельный математик той эпохи, Гёста Миттаг-Леффлер, в конце концов отказался принять к публикации работу Кантора, заявив, что она на сто лет опережает свое время. Такой отказ, полученный от глубоко уважаемого им математика, был чрезвычайно сильным ударом для Кантора. Постоянная борьба с авторитетами, битва с тайнами бесконечности, а также смерть матери, брата и в довершение всего младшего из детей Кантора не прошли даром. Кантор страдал приступами маниакально-депрессивного психоза, и математические споры только усугубляли его состояние. Он был госпитализирован в клинику нервных болезней в Галле и провел там большую часть последних десятилетий своей жизни. Разочаровавшись в математике, он занялся религиозными вопросами, а также уделял много времени попыткам доказать, что подлинным автором пьес Шекспира был Фрэнсис Бэкон.
Но предчувствие Миттаг-Леффлера в некоторых отношениях оказалось правильным. Сто лет спустя идеи Кантора считаются одним из самых прекрасных и удивительных достижений за последние триста лет. Кантор позволил математикам прикоснуться к бесконечности, играть с ней, использовать ее в вычислениях, наконец, признать, что бесконечность – это число. И даже не одно число, а бесконечное множество чисел.
Но для самого Кантора бесконечность была не просто идеей, порожденной разумом:
Я настолько за актуальную бесконечность, что вместо того, чтобы допускать, как это делают обычно, что природа ее ненавидит, считаю, что эта бесконечность проявляется в природе всюду, чтобы выразить совершенства ее Творца. Так, я думаю, что не существует никакой части материи, которая не была бы не только делима, но и фактически разделена, а значит, и наименьшую частицу нужно рассматривать как некий мир, заполненный многими различными творениями.
Вот оно есть, а вот его нет!
Совершенное Кантором открытие всех этих уровней бесконечности привело к появлению вполне реального примера задачи, которая не могла быть решена в рамках существующих аксиом математики – утверждения без доказательства, непроверяемого, лежащего за пределами того, что мы можем знать. Этот вопрос касался самой сути того, что мы называем числом, и показал, насколько числа на самом деле непросты.
Кантор хотел узнать, существуют ли множества чисел, обладающие большим размером, чем множество целых чисел, но все же достаточно малые для того, чтобы невозможно было установить их попарное соответствие со всеми бесконечными десятичными дробями. Другими словами, существует ли племя, члены которого помечены числами так, что оно превосходит племя целых чисел, но проигрывает племени бесконечных десятичных чисел? Бесконечность всех бесконечных десятичных чисел называют континуумом. Гипотеза о континууме утверждает, что не существует бесконечности, меньшей континуума, но большей бесконечности всех целых чисел.
Гильберт был настолько поражен гипотезой о континууме, что поместил проблему определения существования промежуточной бесконечности во главу своего списка из 23 задач, которые предстояло решить математикам XX в.
Кантор мучился этим вопросом всю свою жизнь. В какой-то момент он был убежден, что нашел доказательство того, что никакой бесконечности между этими двумя не существует. Но затем он нашел в нем ошибку. На следующий день он решил, что доказал обратное: промежуточная бесконечность существует. Как всегда верил сам Кантор, «в математике умение задавать вопросы ценнее, чем умение решать задачи».
Так оно и оказалось. Затруднения Кантора были связаны с тем, что оба ответа были правильными.
Решение этой задачи, полученное наконец в 1960-х гг., потрясло математическое сообщество до основания. Пол Коэн, логик из Стэнфорда, продемонстрировал, опираясь на работы Гёделя, что на основе аксиом, которые мы используем в нашей нынешней математике, невозможно доказать, существует ли множество чисел, размер которого находится строго между количеством целых чисел и количеством бесконечных десятичных дробей. Более того, он создал две разные модели чисел, которые удовлетворяли аксиомам математики: в одной из этих моделей ответ на вопрос Кантора был утвердительным, а в другой – отрицательным.
Не знаю, как Кантору понравился бы такой вывод. Он когда-то заявил: «Сущность математики заключается именно в ее свободе». Но не слишком ли большой оказалась эта свобода? Получилось, что существует не один, но несколько видов математики!
Некоторые считают этот момент аналогичным открытию существования множества разных видов геометрии в дополнение к евклидовой. В геометрии Евклида справедлив постулат о параллельных, в отличие от новых сферических и гиперболических геометрий. А теперь мы поняли, что существуют и разные модели чисел и некоторые из них содержат промежуточные бесконечности, а некоторые их не содержат.
И тем не менее математики испытали большое потрясение. Мы-то думали, что знаем числа. Пусть такие числа, как квадратный корень из двух или π, иррациональны и имеют бесконечное десятичное представление, но нам казалось, что эти числа можно увидеть, отметить на линейке. Так что в случае чисел, которые мы знаем, казалось бы, должен иметься и ответ на вопрос Кантора. Есть ли на этой линейке подмножество чисел, строго большее, чем множество целых чисел, но строго меньшее, чем множество всех бесконечных десятичных чисел? Большинство математиков считало, что ответ должен быть «да» или «нет», но не «и да и нет». Но, несмотря на это, было доказано, что доказать ни то ни другое невозможно. Коллега Коэна Джулия Робинсон писала ему: «Ради бога, ведь есть лишь одна истинная теория чисел! Это мое религиозное убеждение». Интересно, однако, что, прежде чем отправить письмо, она зачеркнула последнее предложение. Но Кантора такая неопределенность, вероятно, не затруднила бы, потому что его религиозным убеждениям не противоречило приятие того, что превосходит человеческое знание.
Сколь многие из еще неразрешенных задач, остающихся в наших книгах по математике, окажутся недоказуемыми? Чтобы справиться с некоторыми из этих великих нерешенных задач, нам могут понадобиться новые аксиомы, которые позволят им стать доказуемыми. Гёдель считал, что именно в этом может крыться причина трудности доказательства гипотезы Римана, величайшей из нерешенных задач математики. Он сомневался в достаточности имеющихся у нас аксиом для преодоления многих из проблем теории чисел:
Мы сталкиваемся с бесконечной последовательностью аксиом, которая может быть продолжена все дальше и дальше, и никакого конца ей не видно […] Правда, в нынешней математике высшие уровни этой иерархии практически никогда не используются […] вполне возможно, что это свойство современной математики как-то связано с ее неспособностью доказать некоторые фундаментальные теоремы, например такие как гипотеза Римана.
И да и нет
Теорема Гёделя о неполноте – это увлекательнейший микрокосм задачи доказательства истины. В отсутствие непротиворечивой аксиоматической системы в теории чисел неизбежно будут существовать истинные утверждения, истинность которых не может быть доказана. Интересно отметить, что, если работать вне системы, можно даже доказать, что некоторое утверждение истинно, но недоказуемо внутри этой системы. Можно сказать: почему бы тогда не перейти в бо́льшую систему? Но Гёдель гарантирует, что и в такой большей системе будут свои недоказуемые истинные утверждения, требующие выхода за пределы уже этой системы. Получается очень знакомая бесконечная регрессия.
Эта ситуация созвучна со многими из тех проблем, с которыми мы разбирались раньше. Может быть, понять Вселенную невозможно, пока мы остаемся внутри ее системы. Если Вселенная описывается квантовой волновой функцией, необходимо ли находиться вне системы, чтобы наблюдать ее? Из теории хаоса следует, что мы не можем понять часть системы как отдельную проблему, потому что электрон, находящийся на другом конце Вселенной, может оказать на хаотическую систему влияние, которое отправит ее в совершенно другом направлении. Чтобы рассмотреть всю систему, необходимо находиться вне ее. Та же проблема касается вопроса о понимании сознания. Мы заперты внутри собственной головы, своей собственной системы, и не имеем доступа к сознанию других. То же, по мнению некоторых, ограничивает и наши возможности постижения такой вещи, как существование Бога, трансцендентного относительно мира, в пределах которого мы заключены.
Другой важный аспект работы Гёделя состоит в том, что в пределах аксиоматической системы теории чисел невозможно доказать, что эта теория согласованна, что она не содержит противоречий. Это же может относиться и к вопросу о действенности методов, которые мы используем для получения знаний о Вселенной. Например, любая попытка объяснить, почему индукция – это правильный метод изучения физических явлений, будет основана на применении индукции. Получается настоящий замкнутый круг.
Однако не все следствия такой ограниченности возможностей математического метода столь мрачны и пессимистичны. Можно сказать, что она привела к открытию того удивительного факта, что существуют такие утверждения о свойствах чисел, которые можно либо считать истинными, либо считать ложными, причем оба эти предположения вытекают из закономерных моделей математики; то есть что существует множество разных видов математики. Можно ли сделать то же самое, когда мы встречаем действительно непознаваемый вопрос об устройстве Вселенной? Если мы найдем вопрос, ответ на который действительно невозможно узнать, было бы вполне логично исходить из гипотезы о том, что этот ответ может быть таким или другим. Выбор рабочей гипотезы отчасти зависит от вероятности одного или другого ответа. Но в некоторых случаях вероятности могут быть несущественны, и наш выбор попадает в зависимость от личных отношений с последствиями работы в рамках данной системы.
Математики свободны от такой необходимости выбора. Я как математик легко могу переходить от одной математической модели к другой, если каждая из этих моделей сама по себе внутренне непротиворечива, хотя они и противоречат друг другу. Например, я могу работать в предположении истинности или ложности гипотезы континуума. Если исходная модель непротиворечива, то непротиворечивы и обе математические модели. Если это необходимо для моей математики, я могу использовать гипотезу континуума для исследования этой конкретной математической вселенной. Можно ли поступить так же в отношении других случаев непознаваемого? Если Бог – это то, что не может быть познано, можно ли сделать выбор, который облечет это неизвестное плотью? Но не сделаем ли мы его таким образом познаваемым и не будет ли это противоречить исходному определению?
Выбор гипотезы, из которой мы исходим, следует производить с осторожностью. Нельзя просто предположить, что нечто неизвестное может быть истинно или ложно. Необходимо доказать, что обе такие возможности непротиворечивы. Например, я не знаю, истинна или ложна гипотеза Римана о простых числах, но лишь один из этих вариантов может быть совместим с нашей теорией чисел. Если окажется, что эта гипотеза недоказуема в рамках имеющихся у нас аксиом теории чисел, на самом деле это будет означать, что она истинна. Если она ложна, мы знаем, что ее ложность доказуема, потому что путем конечного систематического поиска мы сможем найти опровергающие ее примеры. Если она ложна, мы не можем работать в модели, предполагающей ее истинность, так как это приведет к противоречиям. Этим и замечательна гипотеза континуума: как она сама, так и противоположное ей утверждение можно включить в согласованную теорию, не порождая никаких противоречий.
Кое-кто утверждал, что те числа, которые мы пытаемся определить аксиоматически, предназначены для измерений, что это те числа, которые могут быть расположены на линейке. Поэтому предположение о том, что гипотеза континуума должна давать лучшее описание того, что мы пытаемся моделировать, может быть вполне обоснованно. Логик Хью Вудин даже выдвинул недавно доводы, объясняющие, почему гипотеза континуума должна быть ложной для тех чисел, которые мы пытаемся моделировать. Он утверждает, что если эти числа представляют измерения, нанесенные на линейку, то есть основания полагать, что из этого следует существование бесконечных подмножеств промежуточного размера между множеством целых чисел и множеством бесконечных десятичных представлений.
Этот пример иллюстрирует напряженность, существующую в отношениях математики и физики. Математика уже несколько столетий прекрасно уживается с существованием множественных математических вселенных – разных, взаимно исключающих математических моделей геометрии или теории чисел. Но физику, даже если он ничего не имеет против идеи множественных вселенных, все же хотелось бы выяснить, какой из этих возможных вариантов описывает ту Вселенную, частью которой мы являемся.
Представим себе, что ученый-естественник, разработав абсолютно непротиворечивую логическую теорию возможного устройства Вселенной, обнаруживает затем, что она не соответствует экспериментальным результатам, полученным в нашей Вселенной. Такую гипотетическую теорию отбрасывают, и после этого она не представляет никакого интереса для научного мира. Если биолог примется писать статью о гипотетическом животном, которое потенциально могло бы существовать, но на самом деле на Земле не встречается, например о единороге, такая статья никому не будет интересна, если только из нее нельзя будет узнать что-нибудь о животных, которые существуют в реальности. Напротив, в математике такие гипотетические миры превозносятся и приветствуются. Они становятся частью все более богатого ассортимента математических возможностей. Естествознание занимается реальным, математика – возможным. Если естественные науки прокладывают единственный маршрут по дереву возможных вселенных, то математика составляет карту, на которую нанесены все возможные пути.
Но что же делать с неразрешимыми вопросами естествознания? В случае гипотезы континуума не имеет смысла выбирать один или другой ответ на основе вероятностных соображений. Не то чтобы один из них был «истинным», а другой нет. Но можно ли сказать то же самое о непознаваемом в физике, в которой «истина» существует?
Интересно отметить, что в случае физики, когда мы встречаем вопрос, недоступный для познания, один из ответов на него соответствует правильному описанию нашей Вселенной, а другой ему не соответствует. Но по самой природе неразрешимого вопроса мы не можем получить никакой новой информации о Вселенной, которая позволила бы нам решить, какое из ее описаний истинно, а какое ложно. Если мы получаем такую информацию, значит, вопрос с самого начала не был неразрешимым. Так что же случится, если мы станем работать, исходя из ложной гипотезы? А ничего! Как и в случае гипотезы континуума, неверный ответ все равно будет согласовываться с имеющейся у нас теорией устройства Вселенной. У вас будет другая история с другими теоремами и результатами. Если при этом возникают противоречия, это позволяет нам установить, что эта концепция ошибочна, а следовательно, данный вопрос не был подлинно неразрешимым.
Например, взять вопрос о бесконечности Вселенной. Если он неразрешим, то Вселенная либо бесконечна, либо конечна и имеет такие размеры, что ее край навсегда останется за пределами нашего горизонта видимости и, таким образом, вне поля наших исследований. Если она бесконечна, к чему приведет работа в предположении о том, что она конечна, но слишком велика, чтобы ее конечность могла быть доказана? Тут интересно то обстоятельство, что если бы такое предположение порождало затруднения, – если бы оно противоречило существующим теориям или новым данным, – мы смогли бы доказать, что Вселенная бесконечна, и этот вопрос не мог бы быть неразрешимым. Разумеется, в математике такой способ прекрасно используется для доказательства идей бесконечности. Мы доказали, что квадратный корень из 2 не может быть выражен в виде отношения двух конечных чисел, исходя из предположения, что это так, и придя в конце концов к противоречию. Возможно, гипотеза бесконечной Вселенной – это единственное предположение, которое не приводит к противоречиям. Может быть, математика снова оказывается лучшим из имеющихся у нас средств исследования отдаленных пределов Вселенной.
На этом «рубеже» мы увидели, как математике удалось помочь нам ориентироваться даже в самой бесконечности. Поразительно сознавать, что бесконечность некогда считали непознаваемой и часто увязывали с идеей Бога. Декарт писал: «Ведь один только Бог может мыслиться мною положительно как бесконечный». И тем не менее поразительные открытия, совершенные Кантором в конце XIX в., дали нам возможность исследовать и сравнивать бесконечности. Бесконечность перестала быть недостижимой. Кантора не смущали те последствия, которые его исследование бесконечности может иметь для вопроса о Боге. Более того, он считал, что Бог избрал его, чтобы возвестить миру эти идеи о бесконечности.
Бесконечность играла и играет ключевую роль в исследовании существования Бога. Например, одно из доказательств существования Бога Фомы Аквинского, известное под названием космологического аргумента, утверждает, что все сущее должно иметь творца, но тогда это положение должно быть применимо и к самому творцу. Чтобы избежать бесконечной регрессии, следует признать, что Бог является решением задачи о первопричине. Но математика позволяет нам создавать все новые и новые бесконечности путем рассмотрения всех уже имеющихся бесконечностей и создания их объединения. Поэтому, в противоположность предположению Аквината, никакого окончания такой цепочки творцов не требуется. Каждый раз мы получаем нечто новое, и этот процесс никогда не прекращается.
Хотя математика успешно продолжает строить новые бесконечности из старых, даже математикам становится очень трудно представить себе масштабы нашей математической вселенной. Большинство из них ограничиваются работой на нижних уровнях бесконечного. Но мы знаем, что они составляют лишь часть никогда не кончающейся иерархии. Это создает некоторые трудности для тех, кто пытается определить Бога как «то, превыше чего ничего невозможно себе представить». В некотором смысле такая сущность невозможна, так как всегда существует способ создать нечто еще более великое. Но если вернуться к идее чего-то, превышающего человеческое воображение, то мы снова приходим к тому, чего мы, люди, знать не можем, – биологическим ограничениям нашей способности знать.
О том, чего мы не можем знать
Итак, нашли ли мы к концу нашего путешествия что-то такое, про что можно категорически утверждать, что этого мы знать не можем? То, что мы считали непознаваемым, например вопрос о бесконечности Вселенной, на поверку оказывается не таким уж и неприступным. Математика может помочь нам доказать существование бесконечного при помощи вполне конечных средств. Поэтому, хотя нам, возможно, никогда не удастся исследовать или увидеть то, что находится за пределами конечной сферы, ограничивающей ту часть Вселенной, которой мы физически можем достичь, нам, предположительно, удастся узнать, что находится за ней, одной лишь силой разума.
Понимание природы времени до Большого взрыва было другим рубежом, казавшимся неприступным. Но и в этой стене открылись щели. Недавние достижения науки дали нам возможность строить теории и даже, возможно, получать экспериментальные данные о времени, предшествовавшем тому моменту, который мы считаем началом всего. И тем не менее вопрос о том, имеет ли время начало или простирается в прошлое бесконечно, по-видимому, еще нескоро спишут из учетных ведомостей науки.
Напротив, кажется, что бесконечно малое, заключенное в сердце структуры игральной кости, которую я держу в руке, никогда не будет полностью познано. Каждое следующее поколение считало, что оно-то добралось до неделимой основы, и каждый раз материя распадалась на еще меньшие части. Как мы можем быть уверены, что то, что мы считаем сейчас структурными элементами Вселенной – кварки, электроны, нейтрино, – не окажутся такими же делимыми, как другие частицы, которые мы разобрали, снимая слой за слоем кожуру с луковицы реальности? Действительно, современная квантовая физика устанавливает предел нашего проникновения вглубь структуры моей игральной кости: все, что меньше планковской длины, является запретной зоной. Здесь мы находим рубеж знания, преодолеть который мы не можем.
Про возможность познания рубежа, который образует наше сознание, трудно сказать что-либо определенное. Исчезнет ли эта задача просто потому, что она окажется неправильно сформулированным вопросом? Найдется ли ее решение в стратегии, подобной той, которую ученые использовали для определения сущности жизни? Там оказалось, что нет никакой жизненной силы; есть лишь набор биологических процессов, наличие которого означает, что данное скопление молекул живет. Или же проблема сознания так и останется недоступной для понимания, потому что мы заключены в своем собственном сознании и никогда не сможем проникнуть в сознание другого?
Допустимость невозможности знания, связанной с заключением внутри системы, – общая черта многих из тех вопросов, в которых мы пытались разобраться. В математике есть истины, остающиеся недоказуемыми в рамках своей системы. Выход из системы позволяет познать их, но при этом возникает новая система, содержащая свои собственные недоказуемые истины.
Воспроизводимость квантового эксперимента невозможна, поскольку такой эксперимент невозможно изолировать от той Вселенной, в которой он проводится, а Вселенная эта эволюционирует и изменится к моменту проведения следующего эксперимента.
Даже математика, созданная для понимания поведения игральной кости, не вполне реалистична. Что такое вероятность? Если я брошу кость 600 раз, я могу ожидать, что шестерка выпадет 100 раз. Но я-то хочу бросить ее всего один раз и знать хотя бы что-то о том, что на ней выпадет. Уравнения теории хаоса говорят нам, что будущее во многом зависит от чрезвычайно тонкой настройки далеких десятичных разрядов величин, вводимых в эти уравнения. То есть я никогда не смогу познать настоящее настолько полно, чтобы получить хоть какую-то надежду знания будущего или прошлого.
Физические ограничения человеческого мозга, и даже вычислительной мощности всей Вселенной, ставят пределы познанию вообще, поэтому существуют такие вещи, которые никогда не будут познаны. Но такая непознаваемость не абсолютна. Она похожа на ситуацию со светом, приходящим к нам от дальних пределов Вселенной, – до того, как мы узнали, что расширение Вселенной ускоряется, – стоит только подождать достаточно долго, и свет до нас доберется. Стоит только подождать достаточно долго, и компьютер сможет проработать все доказуемые истины математики. Однако наши исследования рубежей времени заставляют задать вопрос: что, если, пока мы ждем, кончится само время?
В основе многих ограничений знания лежит ограниченность языка, однако это положение может развиваться и изменяться. Разумеется, многие философы считают язык препятствием в рассмотрении проблемы сознания. Одна из таких проблем – понимание квантовой физики, потому что единственный язык, который можно использовать для ориентации в ее идеях, – это математика. Попытки перевести эту математику на язык нашего повседневного опыта и приводят к возникновению того абсурда, который так затрудняет изучение квантовой физики. Поэтому невозможность определения положения и импульса не представляет собой подлинной непознаваемости. Это скорее неудача перевода с языка математики на естественный язык.
Но следует всегда помнить, что мы связаны тем образом мышления, который присущ нашему историческому моменту. Конт полагал, что мы никогда не сможем узнать, из чего состоят звезды, – как же он ошибался! Поэтому интересно, не будет ли вернее всего сказать, что мы никогда не сможем точно узнать, чего именно мы знать не можем.
Бог как мнимое число
Как далеко можно зайти, создавая решения, по-видимому, неразрешимых задач? Многие века математики смотрели на уравнение х2 = –1 и считали, что оно не имеет решения. Но потом к нему был применен более изобретательный подход. Давайте создадим решение этого уравнения. Мы ввели в математическую картину мира мнимые числа, определив число i как квадратный корень из –1. Почему этот прием сработал? Он не породил в теории никаких противоречий. Мы вплели эту концепцию в уже знакомую нам математику и стали узнавать свойства i. И, что самое важное, оно открыло нам доступ в новые, захватывающие части мира математики. Если бы мы не допустили существования в математике мнимых чисел, это ограничило бы его размеры и возможности. Но не менее важно не приписывать концепции более широкие возможности, чем она имеет.
Что, если попробовать применить более творческий подход к некоторым из наших непознаваемых вопросов? Например, что будет, если определить Бога как ответ на вопрос «Почему существует нечто, а не ничто?». Такая концепция не предполагает ничего, кроме ответа на этот вопрос, то есть ее определения. У нее нет никаких других свойств. Это все то же неизвестное. Даже если мы узнаем еще что-то об ответе на этот вопрос, это будет значить только, что мы узнали больше о таком Боге, которого мы определили как ответ на вопрос «Почему существует нечто, а не ничто?».
Но такой подход следует применять с осторожностью. Если мы записали математическое уравнение, это не значит, что у него есть решения. Введение новой концепции, позволяющей решить уравнение х2 = –1, было продуктивно, потому что оно открыло доступ к новой непротиворечивой математике. С точки зрения платоника, эта идея существовала всегда, ожидая, пока ее выскажут; по мнению прочих, это был акт творчества, обогативший мир нашей математики. Но, если выписать уравнения Великой теоремы Ферма и попытаться определить новые числа, которые будут решениями этих уравнений, мы получим утверждения, которые противоречат самим себе. В конце концов, именно так Уайлс доказал, что эти уравнения не имеют решений.
Проблема большинства религий заключается в том, что Богу придают слишком много свойств, не имеющих никакого отношения к его определению. Мы как бы пытаемся восстановить картину в обратную сторону, сосредоточиваясь на странных свойствах, наколдованных многими поколениями, но не понимая толком, каким было исходное определение. Мы встречаем эту искаженную картину еще в раннем детстве, и, когда мы спрашиваем: «Почему есть нечто, а не ничего?» – она не дает ответа. Но в том-то и дело, что нам показывали не ту картину.
Именно поэтому я называю себя атеистом. С моей точки зрения, это значит, что я отвергаю те классические решения, которые религия, по-видимому, предлагает для ответа на неразрешенные вопросы. Но, может быть, мне не следовало бы отбрасывать все скопом. Раз есть вещи, которые навечно останутся неизвестными, то, возможно, Бог и существует. Традиционное возражение против идеи «Бога белых пятен» состоит в том, что мы стремимся познать Бога, установить личные отношения с этой концепцией. А такой Бог, трансцендентный или незнаемый по определению, по тому же определению исключает всякую возможность познания.
Но беда в том, что такое определение Бога никуда особо не ведет. Если определение числа, квадрат которого равен –1, породило широкий спектр следствий, то определение чего-то как ответа на вопрос «Почему есть нечто, а не ничто?» не порождает ничего нового. Для этой сущности приходится изобретать свойства, не вытекающие из ее определения. Как сказала Карен Армстронг, такой Всевышний слишком высок.
Существует несколько возможных реакций на идентификацию непознаваемого. Одна из них – оставить все как есть: раз что-то непознаваемо, оно не может быть познано. Но всегда существует искушение сделать выбор в пользу одного или другого ответа и жить в соответствии с таким выбором. Возможно, наиболее логически непротиворечивое решение заключается в приятии существования множественных миров и допущении параллельного существования нескольких разных ответов вплоть до момента, когда новые идеи вызовут коллапс этих возможностей. Математики вполне хорошо чувствуют себя и в математике, в которой гипотеза континуума истинна, и в параллельной ей математике, которая предполагает ее ложность.
И все же я не уверен, не изменилось ли мое решение считать себя атеистом к концу этого исследования пределов знания. Если я определяю Бога как существование того, чего мы знать не можем, то называть себя атеистом – значит верить, что ничего непознаваемого не существует. А я в это, кажется, больше не верю. Мне кажется, что в некотором смысле я доказал существование Бога. Дальше речь идет об исследовании тех качеств, которыми такой Бог обладает.
Декларация моего атеизма – это на самом деле реакция на ту довольно выхолощенную версию Бога, которую предлагает нам большинство религий и культур. Я отвергаю возможность существования сверхъестественного разума, вмешивающегося в эволюцию Вселенной. Тем самым я отвергаю Бога, которому приписывают странные свойства – сострадание, мудрость, любовь, – не имеющие никакого смысла в той идее, которую я исследую.
Такая позиция и такое определение, скорее всего, не устроят ни одну из сторон этой дискуссии. Воинствующие атеисты вообще не допустят обсуждения чего бы то ни было, называемого Богом, а верующие сочтут определение Бога как неизвестного бессильным и не имеющим отношения к делу. Как же можно взаимодействовать с таким «Богом белых пятен»?
Возможно, самый важный вывод состоит в необходимости поддерживать шизофренически расколотое состояние ума. Множественные разумы. Казалось бы, мы, люди, вынуждены признать, что не можем знать всего. Знание имеет доказуемые пределы. Такое унизительное понимание важно с интеллектуальной точки зрения, потому что, не будь его, мы жили бы в плену иллюзий и ложной гордыни. Однако другой вывод состоит в том, что мы не всегда можем знать, что именно навечно останется за пределами нашего понимания. Именно поэтому для ученого так важно не сдаваться прежде времени. Верить в то, что мы сможем найти ответы. Верить, что, может быть, мы все-таки можем познать всё.
Четно или нечетно количество моих игральных костей?
Наше путешествие по науке выявило несколько весьма труднопреодолимых рубежей познания. Но помимо этого остается и фундаментальный эпистемологический вопрос: можем ли мы вообще знать хоть что-нибудь? 2000 лет назад Сократ заявил: «Истинное знание состоит в том, что мы ничего не знаем». Признание собственного незнания есть единственное истинное утверждение о знании.
Философы написали многие тома, пытаясь разобраться с теорией познания и установить, что же мы можем знать, определить, что мы называем знанием. Платон предложил определить знание как «обоснованное истинное мнение», но Бертран Рассел, а затем, в 1960-х гг., американский философ Эдмунд Гетье усомнились в том, что это определение действительно отражает сущность знания.
В классическом примере, предложенном Бертраном Расселом, речь идет о женщине, которая смотрит на часы, показывающие два часа. Поэтому она считает, что сейчас два часа. Ее мнение кажется обоснованным, поскольку это время показывают часы. И в этот момент действительно два часа. Но часы на самом деле остановились 12 часов назад, и то, что женщине случилось посмотреть на них именно через 12 часов после этого, – простое совпадение.
Гетье создал сходные сценарии «обоснованного истинного мнения». Вы смотрите на поле и, как вам кажется, видите там корову. Вы делаете вывод, что в поле пасется корова. На самом деле корова в поле есть, но вы ее видеть не можете, потому что она находится в ложбине. У вас есть истинное утверждение. Оно основано на обоснованном мнении, и то, что вы видите, несомненно выглядит в точности как корова. Но из истинности сделанного вами утверждения не следует наличия знания.
Мы можем представить себе ситуацию, в которой мы выработали утверждение об устройстве Вселенной, действительно соответствующее истине. Но обоснование этого утверждения абсолютно ложно, хотя оно и привело нас к истинному утверждению. Уж конечно в такой ситуации нельзя говорить о знании истинности этого утверждения. Я не раз придумывал доказательства истинных математических утверждений, содержавшие логические ошибки (которые я надеюсь заметить до отсылки очередной статьи в журнал). Но мои ложные доказательства не могут служить обоснованием моего знания истинности того или иного математического утверждения.
Я не знаю, истинна или ложна гипотеза Римана. Однако несколько человек уже предлагали доказательства, которые, по их мнению, подтверждали истинность этой гипотезы, и представляли для обоснования своего мнения многие страницы уравнений. В большинстве случаев в таких доказательствах обнаруживались ошибки. Когда такие ошибки предъявляют автору доказательства, это разрушает его обоснованное мнение. Но что будет, если такое ошибочное доказательство убедит всех? Предположим, что ошибка чрезвычайно малозаметна. Мы не можем сказать, что мы знаем, что гипотеза Римана истинна, несмотря на наличие у нас обоснованного истинного мнения. Не может же обоснованное истинное мнение проистекать из ложного обоснования.
Некоторые астрономы древности предполагали, что Земля обращается вокруг Солнца, но их обоснования этого факта были ошибочны. В IX в. до н. э. индийский философ Яджнавалкья аргументировал свою веру в гелиоцентрическую систему следующим утверждением: «Солнце привязывает к себе нитью все эти миры – Землю, планеты, атмосферу». Можно ли утверждать, что он знал, что Земля обращается вокруг Солнца?
Я, наверное, соглашусь с моим коллегой по Нью-колледжу Тимоти Уильямсоном, который утверждает в своей книге «Знание и его пределы» (Knowledge and its Limits), что знание следует рассматривать как нечто фундаментальное, неопределимое через другие понятия. Кажется, все мы знаем, что значит слово «знать». Оно – одно из всего лишь приблизительно сотни слов, для которых существует адекватный перевод на все языки мира. Например, такой базовый глагол, как «есть», в это число не входит.
От Уильямсона же я узнал о фантастическом логическом фокусе под названием «парадокс непознаваемости», который доказывает, что если мы не знаем вообще всего, то некоторые истины всегда будут оставаться непознаваемыми по самой своей природе. Этот парадокс приписывают американскому логику Фредерику Фитчу, который опубликовал его в своей статье 1963 г.. Фитч признавал, что исходным источником его рассуждения был на самом деле комментарий анонимного рецензента на его статью, которую Фитч пытался, но так и не смог опубликовать в 1945 г. Многие годы имя рецензента, создавшего эту логическую жемчужину, оставалось загадкой. Однако в результате последующих изысканий обнаружился рукописный экземпляр той самой рецензии, и анализ почерка показал, что ее автором был знаменитый американский логик Алонзо Чёрч, который внес большой вклад в понимание теоремы Гёделя о неполноте.
В рассуждении Чёрча есть отголосок той рекурсивной стратегии, которую использовал Гёдель, но на этот раз речь не идет о математике – только о чистой логике. И если Гёдель доказывает, что существуют математические истины, которые невозможно доказать в рамках конкретной непротиворечивой аксиоматической системы математики, Чёрч заходит на шаг дальше и провозглашает существование истины, которую невозможно познать вообще никакими средствами.
Предположим, что имеется истинное утверждение, об истинности которого мы не знаем. На самом деле таких утверждений множество. Например, мой дом полон игральных костей – в нем есть не только кость из казино, лежащая у меня на столе. Еще есть кости из игры «Монополия», игра «Лудо», кости, завалившиеся за диван, кости, закопанные в том беспорядке, который царит в комнатах моих детей. Я не знаю, четно или нечетно число игральных костей, имеющихся в моем доме. Разумеется, это утверждение само по себе не является неразрешимым вопросом, так как я могу систематически обыскать весь дом и узнать ответ на него. Но так же безусловно, в данный момент я этого ответа не знаю.
А теперь держитесь: каждый раз, когда я перечитываю этот фрагмент, у меня кружится голова. Пусть р – истинное утверждение, выбранное из следующих двух: «В моем доме имеется четное число игральных костей» и «В моем доме имеется нечетное число игральных костей». Я не знаю, какое из этих утверждений истинно, но одно из них должно быть истинным. И из существования непознанной истины можно извлечь существование истины непознаваемой. Непознаваемой истиной является следующее утверждение: «Утверждение р истинно, но неизвестно». Оно несомненно истинно. Почему оно непознаваемо? Потому что его познание означает знание того, что утверждение р истинно и неизвестно, но при этом возникает противоречие, так как утверждение р не может одновременно быть неизвестным и известным. Таким образом, само утверждение «Утверждение р истинно, но неизвестно» представляет собой непознаваемое утверждение. Утверждение р само по себе не является непознаваемым. Как я уже сказал, я могу разыскать все игральные кости, находящиеся в доме, и узнать, четно их количество или нечетно. А вот мета-утверждение «Утверждение р истинно, но неизвестно» непознаваемо. Это доказательство работает во всех случаях, в которых существует что-то истинное, но неизвестное. Единственный выход из этого тупика – уже знать все. Все истины могут быть познаваемы, только когда все истины известны.
Хотя это рассуждение стало известно под названием парадокса, никакого парадокса, как замечает Уильямсон, в нем не содержится. Это попросту доказательство существования непознаваемых истин. И после всех наших путешествий к пределам науки оказывается, что тот пробел, который мы искали, можно получить при помощи хитрого логического трюка.
Можем ли мы знать хоть что-нибудь?
Многие из специалистов по философии познания ставят под вопрос то, как много мы вообще можем знать о чем-нибудь. Шотландский философ XVIII в. Дэвид Юм распознал одну из тех фундаментальных проблем, с которыми мы сталкивались при рассмотрении наших вопросов: то, что мы заключены внутри системы. Пытаясь применить научные методы, чтобы установить, что мы что-то знаем, мы попадаем в замкнутый круг, потому что мы используем научные, логические аргументы для доказательства правомерности этих же самых методов. Рассмотреть их извне невозможно. Витгенштейн выразил это положение в более цветистой манере: «Выше задницы не нагадишь».
А как насчет математики? В ней-то мы обладаем некоторыми знаниями. Разве доказательство не дает нам стопроцентной уверенности в том, что, например, существует бесконечное количество простых чисел? Но даже математические доказательства, хотя в них все явно и открыто, должны быть обработаны человеческим мозгом, чтобы можно было убедиться в их правильности. Что, если мы оказываемся убеждены в справедливости доказательства, которое тем не менее содержит малозаметную ошибку? Разумеется, одно из обстоятельств, идущих нам на пользу, состоит в том, что все фатальные ошибки рано или поздно обнаруживают себя. Но в таком случае не значит ли это, что математика существует в процессе эволюции, так же как и естествознание? Специалист по философии математики Имре Лакатос считает, что так оно и есть. Он разработал философию математики, основанную на модели Карла Поппера, который считал, что науку можно только опровергнуть, но нельзя доказать ее истинность. По мнению Лакатоса, невозможно точно знать, что какое-либо доказательство не содержит еще не найденного малозаметного изъяна.
В его книге «Доказательства и опровержения» разворачивается увлекательный диалог между учениками, изучающими доказательство теоремы Эйлера о соотношении вершин, ребер и граней трехмерного многогранника. Он отражает историю развития этой теоремы, гласящей, что Р = В + Г – 2. Сначала ученикам кажется, что они нашли доказательство. Потом один из учеников предлагает тело с отверстием в середине. С этим телом формула не работает. И доказательство тоже. Это можно интерпретировать так, что доказательство работает только с теми телами, для которых оно предназначено. Но тут вводятся новое доказательство и новая теорема, относящиеся к новой формуле, которая помимо вершин, ребер и граней тела учитывает еще и количество отверстий. Эта история иллюстрирует гораздо более эволюционный подход к математическому знанию, чем допускают многие из математиков, более похожий на процесс исследования в естествознании. Насколько же действен тот или другой метод в поисках истины?
Одно из оснований считать, что наука позволяет получить истинное знание, заключается в истории ее достижений. Естественные науки настолько успешно описывают и предсказывают видимое устройство вещей, что нам кажется, что они приближают нас к пониманию реальности, которая, по мнению многих, все-таки существует. То, насколько хорошо наука предсказывает и объясняет различные явления, есть, наверное, главная мера нашего приближения к истине. Если карта, к которой мы последовательно обращаемся, приводит нас к цели, это вполне надежный признак того, что такая карта точно отражает реальность.
Наука создала очень неплохие карты Вселенной. Благодаря нашим открытиям, касающимся природы гравитации, науке удается исследовать отдаленные планеты. Благодаря нашим открытиям в области клеточной биологии мы получили генную терапию, способную справляться с неизлечимыми ранее болезнями. Мы используем свои открытия, касающиеся времени и пространства, для навигации при помощи GPS. Если где-то научная карта перестает работать, мы готовы перечертить ее контуры в поисках описания, которое действительно поможет нам разобраться в окружающем мире. Тут действует закон естественного отбора, выживания наиболее приспособленных теорий: теория выживает, если она и далее позволяет делать точные предсказания и управлять средой. Может быть, на самом деле наука и не отражает реальность, но никакого другого сравнимого с ней средства у нас нет.
Еще со времен Канта мы вынуждены сражаться с непознаваемостью «вещей в себе». Ограниченность человеческого восприятия, которую подчеркивает та легкость, с которой можно обмануть наши чувства, заставляет задуматься о том, насколько наш мозг вообще может знать что-нибудь о реальности. Не получается ли так, что мы видим все только через очки, в которые смотрим на Вселенную?
Одна из ключевых проблем наших попыток познания мира состоит в том, что знания об окружающем нас мире мы получаем только через свои собственные органы чувств, а затем расширяем эти знания при помощи аналитических рассуждений. Мы изобретаем теории, которые соответствуют всей информации, собранной нашими органами чувств. Изобретение телескопа, микроскопа и сканера фМРТ расширяет возможности восприятия наших органов чувств.
Но что, если во Вселенной существует и то, чего наши чувства обнаружить не могут? На самом деле у нас больше чувств, чем кажется многим: помимо зрения, слуха, вкуса, осязания и обоняния мы обладаем еще так называемым чувством проприоцепции, благодаря которому мы знаем, как наше тело расположено в пространстве. Есть еще чувства, сообщающие нам о внутреннем состоянии организма. Жидкость, находящаяся во внутреннем ухе, позволяет нам чувствовать ориентацию тела относительно направления силы тяжести. Но существуют ли физические явления, которых мы не замечаем, потому что у нас нет органов чувств, которые могли бы взаимодействовать с ними?
Представим себе организм, не имеющий ни глаз, ни нейронов, способных регистрировать свет. Если у него нет никаких средств обнаружения электромагнитных волн, как он может разработать теорию электромагнетизма? Мы весьма успешно использовали сочетание своего зрения, позволяющего нам видеть некоторую часть электромагнитного спектра, с математическим анализом для вывода заключений о других областях этого спектра. А потом мы разработали приборы, способные обнаруживать такие волны и преобразовывать их в форму, которую мы можем интерпретировать. Но как бы мы смогли начать этот процесс, не имея доступа к некоторой части этого спектра, который дают нам органы зрения?
Вполне возможно, что ограниченность наших чувств также ограничивает возможности наших познаний в математике. Хотя вся математика существует только в уме, одна из научных школ полагает, что поскольку наш разум – это в конечном счете разум, воплощенный в теле, то знание, которое мы можем получить о математике, ограничено тем, что может быть физически воплощено. Безусловно, многое из того, что мы знаем о математике, происходит из описаний физического мира. Взять те же мнимые числа – казалось бы, какое у них может быть физическое воплощение? И тем не менее в конечном счете они происходят из измерений размеров геометрических фигур. Именно попытки понимания длины диагонали грани моей кубической игральной кости привели вавилонян к рассмотрению квадратного корня из 2. А уж оттуда началось путешествие, приведшее нас к идее квадратного корня из –1.
Некоторые поборники идеи искусственного разума утверждают, что для создания разума, сравнимого с нашим собственным, необходимо, чтобы он имел телесное воплощение. Другими словами, мозг, живущий исключительно внутри жесткого диска компьютера, не может породить разум, подобный нашему, без физического взаимодействия с миром через тело. Эта гипотеза снова бросает нам вызов. Могут ли в самом деле существовать некие части математического мира, до которых мы не сможем добраться, потому что они не вытекают из концепций, имеющих физическое воплощение?
И все же остается глубоко философский вопрос о том, насколько наши чувства позволяют нам точно знать что бы то ни было. Мы уже знаем, что наши чувства можно обмануть, заставить нас поверить в реальность вещей, которые на поверку оказываются иллюзией. Как, например, мы можем быть уверены в том, что Вселенная, которую мы воспринимаем, – не имитация? Как мы видели на шестом «рубеже», человеку можно внушить, что он находится в чужом теле. Так как же мы можем быть уверены, что мы – не мозги в банке, в которые компьютер закачивает искусственно созданную чувственную информацию, а окружающий нас мир – не подделка?
На такие попытки поставить под сомнение все то, что мы знаем, я могу ответить, что в этой книге я хотел исследовать, как мы можем узнать что-либо об этой имитации. Кант считал, что истинное устройство мира навсегда останется сокрытым от нашего взора. Мы можем познать лишь кажущееся его устройство. Мне кажется, что большинство ученых какое-то время читает об этом споре об онтологии и эпистемологии и слушает философов, выражающих сомнение в том, что наука рассказывает нам, как на самом деле устроен мир. А потом они возвращаются к своим исследованиям, думая, что, даже если мы никогда не сможем узнать, какова на самом деле реальность, нужно по меньшей мере попытаться выяснить, какова эта реальность в представлении наших органов чувств. В конце концов, именно это на нас и воздействует.
Поэтому, наверное, лучшее, что мы можем надеяться получить от науки, – это правдоподобное знание о Вселенной; то есть наука дает нам теорию, которая, по-видимому, описывает реальность. Мы считаем, что теория, которая позволяет истолковать наше восприятие мира, должна быть близка к истине, хотя философы и уверяют нас, что мы никогда не сможем знать наверняка. Как сказал Нильс Бор: «Неверно думать, что задача физики – в том, чтобы обнаружить, какова природа. Физика касается того, что мы можем сказать о природе».
Здесь водятся драконы
Но как же насчет того, чего мы знать не можем? Если что-то не поддается научному исследованию, если оно непознаваемо, то, может быть, с таким непознаваемым лучше справится какая-то другая дисциплина? Вот, например, что говорит о вопросе «чего-то, а не ничего» Мартин Рис: «Важнейшая проблема сводится к вопросу о том, почему что-то вообще существует. Что вдыхает жизнь в уравнения и вызывает их воплощение в реальном космосе? Однако такие вопросы лежат вне пределов науки: они относятся к ведению философов или богословов».
Возможно, такое заявление свидетельствует о слишком поспешном признании своего поражения, но верно и то, что наука процветает там, где мы делимся непознаваемым с другими дисциплинами. Если непознаваемое воздействует на то, как мы живем, то при выборе ответа на такой неразрешимый вопрос имеет смысл изучить его последствия. Музыка, поэзия, литература и искусство вносят важный вклад в изучение следствий непознаваемого.
Взять вопрос о бесконечности Вселенной. Если вы считаете, что пространство продолжается бесконечно, из этого можно вывести некоторые весьма интересные следствия. Тот факт, что где-то во Вселенной может существовать бесконечно много экземпляров вас, читающего эту книгу, может сильнейшим образом повлиять на вашу жизнь, даже если вы никогда не узнаете, так ли это.
Из теории хаоса следует, что не только игральная кость, но сам человек некоторым образом составляет часть непознаваемого. Хотя каждый из нас – это физическая система, никакое количество данных не позволит нам полностью предсказать человеческое поведение. Гуманитарные дисциплины – это лучший из имеющихся у нас языков для понимания того, что мы вообще можем понять о том, что значит быть человеком.
Исследования сознания обнаруживают границы, дальше которых нам не зайти. Наш внутренний мир потенциально непознаваем для других. Но разве не поэтому – в том числе – мы пишем и читаем романы? Именно они дают другому человеку наиболее действенное средство для проникновения в этот внутренний мир.
То, чего мы знать не можем, создает пространство для существования не только науки, но и мифа, предположения, воображения. Пусть мы чего-то не знаем, но это не мешает нам строить гипотезы, заполняющие эту неизвестность, и эти гипотезы дают нам жизненно важный материал для формирования того, что когда-нибудь может стать известным. Без таких гипотез у нас не было бы никакой науки.
Витгенштейн заканчивает свой «Логико-философский трактат» знаменитой фразой: «О чем невозможно говорить, о том следует молчать». На мой взгляд, это пораженческое высказывание, и сам Витгенштейн впоследствии считал так же. Лучшей развязкой было бы что-нибудь вроде: «О чем невозможно знать, то можно вообразить». В конце концов, именно с воображения, с гипотез начиналось наше путешествие к познанию того, что мы знаем.
И стимулом этого путешествия всегда было то, чего мы не знаем. Как заявил Максвелл: «Любому подлинному достижению в науке предшествует полностью осознанное невежество». Я безусловно согласен с этим утверждением в приложении к математике. Чтобы сохранить свою убежденность, когда я отправляюсь в неизвестное, мне необходимо верить, что решение существует и я смогу его найти. Знать, что мы чего-то не знаем, жизненно важно для продвижения вперед. Стивен Хокинг также сознает опасность веры в то, что мы знаем все: «Главный враг знания – не невежество, а иллюзия знания».
С моей точки зрения, источник жизненной силы математики – это ее гипотезы, то, чего мы еще не доказали. Именно то, чего я не знаю, побуждает меня продолжать математические поиски. Я хочу узнать, справедлива ли гипотеза Римана и ложна ли гипотеза PORC, которую я исследую в течение последних нескольких десятилетий. Как сказал Джейкоб Броновски, «человеческое знание – дело личное и важное, бесконечное путешествие на грани неопределенности».
Важность наличия еще не достигнутых целей хорошо иллюстрирует то, как странно реагируют многие математики на найденное наконец доказательство одной из великих математических теорем. Завершение математических поисков может вызывать своего рода меланхолическое чувство, подобное той грусти, которую ощущаешь, дочитав великий роман. Мне кажется, что нам так нравилась трудность теоремы Ферма, что решение этой задачи, которым Эндрю Уайлс завершил длившиеся 350 лет поиски, было встречено со смешанным чувством восторга и печали.
Важно сознавать, что в нашей жизни должно существовать неопределенное, неизвестное, непознаваемое. Даже если в конце концов нам удастся создать теорию, описывающую, как устроена Вселенная, мы никогда не будем уверены, что в этой истории нет следующей главы, которая еще ждет своего открытия. Мы никогда не будем знать, что дошли до конца. Как бы нам ни хотелось определенности, в науке мы должны всегда быть готовы оставить уже известное на данный момент и двигаться дальше. Именно поэтому наука жива и никогда не окостенеет.
Поэтому, может быть, мне следует смириться с тем, что, когда я катаю игральную кость в своей руке, ее будущее неопределенно. И когда она наконец выпадает из моей ладони, возможно, именно незнание того, что на ней выпадет, заставляет меня смотреть, как она падает на стол и катится по нему.
Назад: 13
Дальше: Выражение признательности

