Мне надоел неинтересный ассортимент рождественских хлопушек, которые можно купить в магазинах, и в этом году я решил побаловать свою семью самодельными математическими хлопушками. В каждой из них были спрятаны математическая шутка или анекдот и математический парадокс. Моей семье показалось, что в шутках было больше математики, чем юмора. Судите сами… Сколько нужно математиков, чтобы поменять лампочку? 0 и 9 в периоде. Если вам не смешно, не беспокойтесь. Мои родные тоже не смеялись. Если вы не поняли, в чем тут соль, – хотя объяснять шутки вообще-то не следует – дело в том, что можно доказать, что бесконечная десятичная дробь 0,999… на самом деле равна 1.

Парадоксы были несколько интереснее. Один из них касался ленты Мебиуса, парадоксального на вид геометрического объекта, у которого есть всего лишь одна сторона. Если взять длинную полоску бумаги и, перекрутив ее, соединить концы, полученное кольцо будет односторонним. В этом можно убедиться, попытавшись закрасить ее стороны: начав закрашивать одну сторону, вы скоро обнаружите, что закрасили всю петлю. Другое удивительное свойство ленты Мебиуса заключается в том, что, если ее разрезать посередине, она не распадается на два отдельных кольца, как можно было бы ожидать, а остается целой. Она по-прежнему будет единой петлей, но теперь будет содержать два переворота.

Хлопушка, которая в результате досталась мне самому, была тем не менее очень неплохой – сам себя не похвалишь… Даже шутка была смешной: «Что значит инициал “Б.” в имени Бенуа Б. Мандельброта? – Бенуа Б. Мандельброт». Если вам все еще не смешно, вы, наверное, не учли, что именно Мандельброт открыл фракталы, о которых мы говорили на первом «рубеже», геометрические формы, структура которых не упрощается, сколько их ни увеличивай. А парадокс я взял из своих самых любимых. Он состоит из двух утверждений, приведенных в начале этой главы, записанных на разных сторонах одной и той же карточки. Меня всегда в равной степени восхищали и тревожили такого рода словесные игры. Одна из любимых книг моего детства называется «Как же называется эта книга?». Она была полна безумных языковых игр, многие из которых, начиная с ее названия, использовали логические следствия из рекурсивных ссылок.

Со временем я научился не удивляться образованным в естественном языке фразам, которые порождают парадоксы, подобные логическому порочному кругу, образованному двумя предложениями на карточке из моей рождественской хлопушки. Сама возможность формировать осмысленные предложения не означает, что каждому такому предложению всегда можно приписать истинное значение, имеющее смысл.

Мне кажется, что такая скользкая природа языка была одной из причин, по которым меня привлекла точность математики, в которой такие двусмысленности недопустимы. Но, как я объясню в этой главе, один из величайших специалистов по математической логике всех времен, Курт Гёдель, доказал именно при помощи парадокса из моей хлопушки, что даже моя собственная наука содержит истинные утверждения о числах, истинность которых мы никогда не сможем доказать.

Такое стремление к уверенности, к знанию – подлинному знанию – было одной из главных причин, по которым я предпочел математику всем остальным наукам. В естественных науках то, что, как нам кажется, мы знаем о Вселенной, – это модели, соответствующие экспериментальным данным. Модели, которые могут стать научными теориями, должны допускать возможность опровержения. Теории выживают – если они выживают – тогда, когда все имеющиеся данные соответствуют их модели. Если мы получаем новые данные, противоречащие модели, мы должны сменить модель. Научная теория по самой своей природе предполагает возможность оказаться отвергнутой. Но можем ли мы в таком случае на самом деле быть уверены в своей правоте, хоть когда-нибудь?

Когда-то мы считали, что Вселенная статична, но потом произошли новые открытия, доказавшие, что галактики разбегаются от нас. Мы полагали, что скорость расширения Вселенной уменьшается вследствие воздействия гравитации. Затем мы выяснили, что ее расширение ускоряется. Мы ввели в свою модель идею темной энергии, стремящейся раздвинуть Вселенную во все стороны. Эта модель еще ждет доказательства своей неправоты, хотя пока что вновь появляющиеся экспериментальные данные все более подтверждают ее. В конце концов мы можем найти истинную модель Вселенной, которую не смогут поколебать никакие новые открытия. Но мы никогда не сможем быть уверены в том, что справедлива именно эта модель.

В этом и состоит одна из наиболее интересных черт естественных наук – они постоянно развиваются, в них всегда появляется что-то новое. Мы можем сочувственно относиться к старым теориям, утратившим свое значение. Разумеется, новые теории вырастают из старых. Ученый постоянно опасается, что его теория, модная в данный момент и получающая многочисленные премии, внезапно может оказаться вытеснена чем-то новым. Модель атомного пудинга, идея абсолютного времени, одновременная определимость положения и импульса частиц – все они давно покинули вершину списка научных бестселлеров. Их заменили новые теории.

Та модель Вселенной, о которой я читал в школе, с тех пор была полностью переписана. Однако с математическими теоремами, которые я учил в то же время, ничего такого не произошло. Они столь же справедливы сегодня, как и в тот день, когда я их впервые прочел, как и в тот день, когда они были открыты. А с этого дня в некоторых случаях прошло целых 2000 лет. Меня, неуверенного в себе прыщавого подростка, особенно привлекала такая определенность. Это не означает, что математика статична. Она постоянно развивается по мере того, как неизвестное становится известным, но такое известное остается известным и устойчивым, образуя первые страницы очередной великой истории. Почему же процесс достижения математической истины столь отличен от того, с чем имеет дело естествоиспытатель, не имеющий надежды получить окончательное знание?

Самый важный ингредиент на кухне математика – это доказательство.

Существуют свидетельства того, что люди занимались математикой уже во 2-м тысячелетии до н. э. На вавилонских глиняных табличках и египетских папирусах находятся сложные вычисления и решения задач: оценки значения π, формула расчета объема пирамиды, алгоритмы решения квадратных уравнений. Но, как правило, эти документы описывают процедуры, пригодные для решения конкретных задач. Мы не находим обоснований того, почему такие процедуры всегда работают, за исключением убедительных свидетельств того, что они успешно работали в тысячах предыдущих случаев, зарегистрированных на более ранних глиняных табличках. Математическое знание было основано на опыте и обладало скорее естественнонаучным оттенком. Новые процедуры разрабатывались, если возникала задача, которую нельзя было решить при помощи уже известных алгоритмов.

Затем, в районе V в. до н. э., положение дел начало изменяться, когда за эту тему взялись древние греки. В дополнение к алгоритмам стали появляться рассуждения, обосновывавшие, почему та или иная формула всегда работает, как указано на упаковке – или на глиняной табличке. Такое обоснование уже не сводилось к тому, что, раз алгоритм сработал последнюю тысячу раз, он, вероятно, будет работать и дальше: рассуждение объясняло, почему данное утверждение всегда будет справедливым. Так появилась идея доказательства.

Первым известным автором математического доказательства считается Фалес Милетский. Он доказал, что если взять любую точку на окружности и соединить ее с двумя концами диаметра этой окружности, то полученный угол всегда будет прямым. Какую бы окружность вы ни взяли, какую бы точку на ней ни выбрали, вы всегда получаете в точности прямой угол. Не приблизительно прямой, и не потому, что так, по-видимому, получается на всех ваших чертежах. Этот результат следует из свойств окружностей и прямых.

Доказательство Фалеса отталкивается от положений, в справедливости которых его читатель уже уверен и приходит к этому новому элементу знания, который вовсе не кажется изначально очевидным при простом взгляде на окружность, путем изобретательной последовательности логических ходов. Фокус заключается в построении отрезка, соединяющего исходную точку В, лежащую на окружности, с центром окружности О.

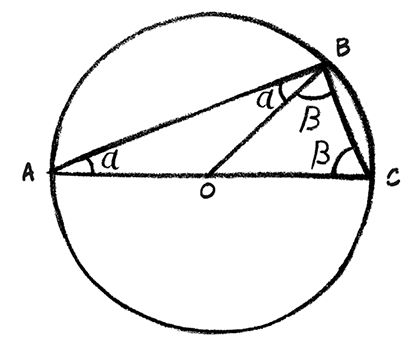
Какая нам от этого польза? Теперь у нас есть два треугольника, каждый из которых имеет две стороны равной длины. Это значит, что противоположные центру окружности углы в каждом из этих треугольников равны. Это свойство таких треугольников к тому времени уже было доказано. Возьмем большой треугольник АВС, который мы начертили в самом начале. Сумма его углов есть 2α + 2β. Тогда, с учетом того, что сумма всех углов треугольника должна быть равна 180°, мы знаем, что α + β = 90°, как и утверждал Фалес.

Когда я впервые увидел это доказательство в детстве, я пришел в настоящий восторг. Из картинки видно, что угол, примыкающий к окружности, похож на прямой. Но можно ли быть в этом уверенным? Мой разум искал какую-то причину, по которой это должно быть так. А потом, когда я перевернул страницу, увидел третий отрезок, который Фалес провел в центр окружности, и осознал логические следствия такого построения, я внезапно понял с ошеломляющей ясностью, почему этот угол действительно должен быть равен 90°.

Заметьте, что уже в этом доказательстве здание математического рассуждения строится на фундаменте положений, которые были доказаны ранее: например, того факта, что сумма углов треугольника всегда равна 180°. Открытие Фалеса, в свою очередь, стало основой для построения следующего этажа математического здания.

Доказательство Фалеса – лишь одно из многих, включенных в «Начала» Евклида. Многие считают эту книгу образцом самой сути математики и математического доказательства. Она начинается с основных структурных элементов, аксиом, геометрических утверждений, которые кажутся настолько самоочевидными, что читатель готов принять их в качестве надежного фундамента, на котором можно начать выстраивать логическое рассуждение.

Идея доказательства не возникла сама по себе, на пустом месте. Она скорее выросла из нового литературного стиля, разработанного в Древней Греции. Искусство риторики, сформулированное Аристотелем и подобными ему авторами, создало новый тип рассуждений, направленных на убеждение аудитории. Шла ли речь о юридических спорах, политических кампаниях или просто литературном повествовании, аудитории предлагалось совершить путешествие по логическому маршруту, в котором оратор пытался убедить слушателей в правоте своей позиции. Математика Египта и Вавилона выросла из строительства и измерения новых городов, возникавших в долинах Нила и Евфрата. Новая потребность в логике и риторических рассуждениях возникла из политических институтов эпохи расцвета греческих городов-государств, лежавших в основе греческой империи.

Для Аристотеля риторика была сочетанием чистой логики с методами, рассчитанными на воздействие на эмоции публики. Математическое доказательство происходит от первого из этих ингредиентов. Однако доказательство также связано с повествованием. И именно поэтому доказательство появилось в этот момент и в этом месте, вероятно, благодаря замысловатым историям, созданным такими драматургами, как Софокл и Еврипид, не в меньшей степени, чем благодаря философским диалогам Аристотеля и Платона.

В свою очередь, математические исследования греков со временем вышли из области практических алгоритмов для строителей и землемеров в сферу удивительных открытий, больше похожих на математические истории, поражающие воображение читателя.

Доказательство – это логическое повествование, уводящее читателя из места, ему известного, в новые, еще неизведанные дали. Подобно приключениям Фродо во «Властелине колец» Толкина, доказательство есть описание путешествия из Шира в Мордор. В пределах давно знакомого Шира находятся математические аксиомы, самоочевидные истины о числах и уже доказанные положения. Они образуют тот пейзаж, с которого начинается странствие. Путешествие, начинающееся с этой привычной территории, происходит по правилам математической дедукции, подобным правилам шахматных ходов, которые определяют, как мы можем перемещаться по этому миру. Время от времени мы можем заходить в тупик и быть вынуждены отклоняться в сторону или даже возвращаться назад, чтобы найти обходной путь. Иногда для продолжения такого путешествия приходится ждать появления новых математических персонажей – например мнимых чисел или методов дифференциального исчисления. Доказательство – это рассказ о путешествии и карта, на которой отмечены координаты этого путешествия. Путевой дневник математика.

Чтобы такое путешествие заняло свое место в математическом эпосе, ему недостаточно достичь истинного утверждения о числах или геометрических фигурах. Оно должно поражать, восхищать, эмоционально затрагивать своего читателя. В нем должны быть опасности и драматическое напряжение. Математика отличается от собрания истинных утверждений о числах так же, как литература не сводится к набору всех возможных сочетаний слов, а музыка – к коллекции всех возможных последовательностей нот. Математика требует применения эстетической оценки и выбора. И наверное, именно поэтому искусство математического доказательства развилось в эпоху расцвета повествования. Возможно, доказательство не в меньшей степени было порождено пафосом, эмоциональной стороной риторики Аристотеля, чем ее логосом, то есть рациональным аспектом.

Хотя многие из первых геометрических доказательств конструктивны, древние греки также использовали свои новые математические инструменты для доказательства невозможности, непознаваемости некоторых вещей. Мы уже видели один яркий пример такого доказательства: квадратный корень из 2 не может быть выражен в виде отношения двух целых чисел.

Это доказательство обладает большой нарративной силой: оно увлекает читателя в путешествие, исходя из предположения, что длина диагонали может быть выражена в виде дроби. По мере невинного на вид развития сюжета мы все дальше и дальше углубляемся в кроличью нору этой истории, пока наконец не доходим до совершенно абсурдного вывода: четные числа есть числа нечетные и наоборот. Мораль сей басни заключается в том, что предполагаемая дробь, выражающая искомую длину, может быть лишь иллюзией. Для желающих совершить путешествие вниз по кроличьей норе эта история изложена в рамке на следующей странице.

Тем, кто впервые встречался с числом, подобным квадратному корню из двух, оно должно было казаться объектом, который по самой своей природе не подлежит полному познанию. Знать число означало записать его, выразить через уже известные числа. Но это число, по-видимому, не поддавалось никаким попыткам записать его значение.

Это был необыкновенный момент в истории математики – создание совершенно нового вида чисел. Можно было упорно утверждать, что уравнение х² = 2 вообще не имеет решения. В то время числа, которые могли дать точное решение этого уравнения, не были известны. Собственно говоря, математический аппарат, достаточно сложный, чтобы придать таким числам смысл, появился только в XIX в. И все же было ощущение, что такое число существует. Его можно было видеть – вот оно, длина стороны треугольника. В конце концов математики решились добавить к нашему математическому инструментарию новые типы чисел, которые позволили нам решать такие уравнения.

Существовали и другие уравнения, казавшиеся нерешаемыми, причем их ответ был не так нагляден, как квадратный корень из двух, – и тем не менее нам удалось создать и такие решения. С современной точки зрения решение уравнения х + 3 = 1 кажется нетрудным: х = –2. Но у греков не было числа, позволяющего выразить это решение. Диофант Александрийский называл такие уравнения абсурдными. По мнению математиков, подобных Диофанту, числа были геометрическими объектами: они выражали реально существующие вещи, длины отрезков. Такого отрезка, длина которого станет равна единице после удлинения на три единицы, не существует.

Другие культуры не так легко признавали свое поражение перед лицом такого уравнения. В Древнем Китае числа использовали для подсчета денег, а там, где дело касается денег, часто возникают и долги. Легко можно представить себе обстоятельства, в которых я добавляю в свой кошелек три монеты и обнаруживаю, что в нем осталась всего одна. Две остальные монеты могли уйти на оплату долга другу. В 200 г. до н. э. китайские математики использовали для представления чисел красные палочки; однако палочки, которые использовали для подсчета долгов, были черными. Отсюда и пошла традиция записывать убытки в бухгалтерских книгах красными чернилами – только где-то по дороге цвета успели поменяться.

Пусть L – длина гипотенузы прямоугольного треугольника, длина обоих катетов которого равна 1. По теореме Пифагора, площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Но площадь обоих меньших квадратов равна 1, а площадь большего квадрата равна L². Таким образом, L есть число, квадрат которого равен 2.

Предположим, что L равно отношению двух целых чисел: L = p/q.

Можно предположить, что одно из чисел p и q – нечетное. Если оба эти числа четные, числитель и знаменатель дроби можно делить на 2 до тех пор, пока одно из чисел не станет нечетным.

Из L² = 2 следует, что p²/q² = 2.

Умножим обе стороны равенства на q²: p² = 2 ∙ q².

Итак, четное число р или нечетное? Мы знаем, что р² – четное число, поэтому и р должно быть четным, так как нечетное число в квадрате также дает нечетное число. Значит, р = 2 ∙ n для некоторого числа п. Раз р – четное число, то q должно быть нечетным. Но подождите секундочку…

2 ∙ q² = p² = (2 ∙ n)² = 2 ∙ 2 ∙ n², и, разделив обе части этого равенства на 2, мы получим: q² = 2 ∙ n².

Вспомним, что раньше мы выяснили, что q – нечетное число.

Значит, и q² должно быть нечетным. Но правая часть этого уравнения равна четному числу! Итак, если длина L может быть выражена в виде дроби, то четность равна нечетности. Поскольку такой вывод явно абсурден, наше исходное предположение о возможности выразить L в виде отношения двух целых чисел должно быть ложным.

По-моему, это одно из самых потрясающих доказательств в математике. Мы показали при помощи конечного логического рассуждения, что существует длина, для выражения которой требуется бесконечное число.

Первая теория отрицательных чисел возникла в VII столетии в Индии. В частности, Брахмагупта установил некоторые важные математические свойства таких чисел, например что «долг, умноженный на долг, приносит богатство» – то есть что минус на минус дает при умножении плюс. Интересно отметить, что это положение – не самостоятельный закон, а следствие из аксиом математики. Его доказательство представляет собой весьма увлекательную задачу. Европейцы убедились в существовании чисел, позволяющих решать уравнения такого рода, лишь к XV в. В XIII в. употребление отрицательных чисел даже было запрещено во Флоренции.

Новые числа появлялись и дальше, особенно когда математики столкнулись с проблемой решения уравнений типа х² = –1. На первый взгляд решение казалось невозможным. Ведь если взять положительное число и возвести его в квадрат, результат будет положительным, а как доказал Брахмагупта, квадрат отрицательного числа также положителен. Когда математики эпохи Возрождения встречали это уравнение, их первой реакцией было предположение о невозможности его решения. И тогда итальянский математик Рафаэль Бомбелли сделал следующий радикальный шаг: он предположил, что существует некое новое число, квадрат которого равен –1. Оказалось, что такое число можно использовать для решения огромной массы уравнений, которые до этого считались нерешаемыми. Интересно, что в некоторых случаях такое мнимое число требовалось лишь в промежуточных вычислениях и не входило в конечный ответ, который содержал только уже привычные, обычные числа, явно дающие решение данного уравнения.

Все это выглядело как математическая алхимия, но многие отказывались допустить новые числа Бомбелли в каноническую математику. Декарт писал о них довольно презрительно, отвергая такие числа как мнимые. С течением времени математики осознали не только их силу, но и тот факт, что их введение в математику, по-видимому, не порождает никаких противоречий. Мнимые числа заняли причитающееся им место в математике только в начале XIX в., отчасти благодаря картинке, которая помогла математикам зримо представить их себе.

Обычные числа (называемые в математике вещественными) были отложены по горизонтальной оси. Мнимые числа, такие как i, как был обозначен квадратный корень из –1, были представлены на вертикальной оси. Эта двумерная картина мнимых, или комплексных, чисел внесла большой вклад в примирение с этими новыми числами. Сила этого представления была подтверждена открытием того факта, что геометрия этой картины отражает арифметику чисел.

Существуют ли еще и другие числа, скрытые за этой гранью, еще не открытые? В надежде открыть другие новые числа можно попробовать рассмотреть другие странные уравнения. Например, как насчет уравнения х⁴ = –1?

Может быть, для решения этого уравнения необходимы какие-то новые числа? Но одна из величайших теорем XIX в., называемая теперь основной теоремой алгебры, доказала, что использование мнимого числа i и вещественных чисел позволяет решить любое алгебраическое уравнение. Например, если взять

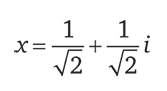
и возвести его в четвертую степень, результат будет равен –1. Мы достигли грани, за которой решение уравнений более не позволяет находить новые числа.

Найденное древними греками доказательство иррациональности квадратного корня из двух было первым из многих математических доказательств невозможности тех или иных вещей. Другое доказательство невозможности касалось так называемой концепции «квадратуры круга». Математическая идея квадратуры круга даже вошла во многие языки в качестве выражения чего-то невозможного. Квадратура круга относится к числу геометрических задач, которые древние греки обожали решать с использованием линейки (без делений) и циркуля (для построения дуг окружностей). Они придумали весьма изобретательные способы построения точных равносторонних треугольников, пятиугольников и шестиугольников при помощи этих инструментов.

Задача о квадратуре круга сводится к построению при помощи этих инструментов квадрата, площадь которого равна площади данного круга. Как греки ни старались, решение этой задачи им не давалось. Столь же неразрешимую задачу задал оракул на острове Делос. Жители этого греческого острова просили оракула посоветовать им, как избавиться от чумы, которую наслал на них бог Аполлон. Оракул ответил, что им следует удвоить размер алтаря Аполлона. Алтарь этот имел совершенную кубическую форму. Платон истолковал это указание как требование построить при помощи линейки и циркуля второй совершенный куб, объем которого был бы вдвое больше объема первого.

Если объем второго куба равен удвоенному объему первого, значит, длина его стороны должна быть равна произведению длины стороны первого куба на кубический корень из двух. Отмерить квадратный корень из двух просто, так как ему равна длина диагонали квадрата с единичной стороной; однако получить кубический корень из двух оказалось так трудно, что жители Делоса не смогли решить эту задачу. Может быть, при помощи геометрии и математики оракул просто хотел отвлечь внимание делосцев от стоявших перед ними более насущных социальных проблем.

Решение задач о квадратуре круга, удвоении куба и трисекции угла (третья классическая задача) оказалось невозможным. Но математики сумели доказать, вне всякого сомнения, что все эти вещи невозможны, только к XIX в. Ключ к доказательству невозможности этих геометрических построений появился лишь с развитием теории групп – языка, используемого для понимания симметрии, который и сам я использую в своих исследованиях. Оказалось, что при помощи циркуля и линейки можно построить только такие отрезки, длины которых являются решениями некоторых типов алгебраических уравнений.

Решение задачи о квадратуре круга требует построения при помощи циркуля и линейки отрезка длиной π на основе отрезка единичной длины. Однако в 1882 г. было доказано, что π – число не просто иррациональное, но трансцендентное, что означает, что оно не является решением никакого алгебраического уравнения. А это, в свою очередь, значит, что квадратура круга невозможна.

Математика очень хорошо умеет доказывать, что что-то невозможно. Одна из самых знаменитых теорем, содержащихся в книгах по математике, – это Великая теорема Ферма, утверждающая, что невозможно найти ненулевые целые числа, удовлетворяющие уравнению

xⁿ + yⁿ = zⁿ,

где натуральное число п больше 2. Это, очевидно, не так в случае n = 2, который соответствует уравнению, выведенному Пифагором для прямоугольного треугольника. Если n = 2, решений существует множество, например 3² + 4² = 5². На самом деле таких решений бесконечно много, и уже древние греки нашли формулу, по которой можно получить все такие решения. Но находить решения часто оказывается гораздо проще, чем доказать невозможность нахождения чисел, которые удовлетворяли бы любым из уравнений Ферма.

Как известно, Ферма считал, что нашел решение, но написал на полях своего экземпляра «Арифметики» Диофанта, что эти поля слишком малы для найденного им замечательного доказательства. Прошло целых 350 лет, прежде чем мой коллега по Оксфорду Эндрю Уайлс наконец смог представить убедительное доказательство того, почему целочисленные решения уравнения Ферма найти невозможно. Доказательство Уайлса занимает более сотни страниц, не считая тысяч страниц ранее разработанной теории, на которой оно основано. Так что для его изложения не хватило бы даже очень широких полей.

Доказательство Великой теоремы Ферма – это проявление подлинного мастерства. Я считаю честью для себя жить в то самое время, когда были найдены последние фрагменты этой головоломки.

До того как Уайлс продемонстрировал невозможность существования решения, все еще сохранялась возможность существования каких-нибудь особо хитрых чисел, которые могут быть решением одного из таких уравнений. Я помню великолепную первоапрельскую шутку, которая гуляла по математическому сообществу примерно в то же время, когда Уайлс объявил о своем доказательстве. Суть шутки состояла в том, что Ноам Элкис, уважаемый специалист по теории чисел из Гарварда, получил неконструктивное доказательство существования такого решения. Это первоапрельское электронное сообщение было написано весьма изобретательно, так как слово «неконструктивное» означало, что он не может прямо назвать числа, являющиеся решением уравнений Ферма, но из его доказательства следует, что решение должно существовать. Самое замечательное состоит в том, что многим это сообщение было переправлено через несколько дней после 1 апреля, когда шутка впервые вышла в свет, так что они понятия не имели, что она имеет отношение к первоапрельским розыгрышам.

Даже и без всевозможных розыгрышей математическое сообщество провело 350 лет, не зная, существует ли такое решение. Мы просто этого не знали. Но Уайлс в конце концов прекратил наши мучения. Его доказательство означает, что, сколько бы мы ни перебирали чисел, мы никогда не найдем такие три числа, которые будут решением одного из уравнений Ферма.

Мы живем в золотой век математики, в течение которого были наконец решены некоторые из величайших нерешенных задач. В 2003 г. российский математик Григорий Перельман решил одну из труднейших задач геометрии, доказав гипотезу Пуанкаре. Однако по-прежнему существует множество утверждений о числах и уравнениях, доказательства которых все еще ускользают от нас: гипотеза Римана, гипотеза парных простых чисел, гипотеза Бёрча – Свиннертон-Дайера, гипотеза Гольдбаха.

Мои собственные исследования, которым я посвятил последние двадцать лет, направлены на выяснение истинности или ложности так называемой гипотезы PORC. Ее сформулировал более 50 лет назад оксфордский математик Грэм Хигман, предполагавший, что число групп симметрии с определенным числом симметрий должно выражаться красивым полиномиальным уравнением (буква Р в аббревиатуре PORC обозначает полином). Например, число групп симметрии с р⁶ симметриями, где р – простое число, дается квадратичным выражением относительно р: р² + 39р + с (где с – константа, которая зависит от остатка от деления р на 60).

Результаты моих собственных исследований заставляют серьезно усомниться в справедливости этой гипотезы. Я открыл симметричный объект с р⁹ симметриями, поведение которого свидетельствует о значительном отклонении от предсказаний гипотезы Хигмана. Но это не дает окончательного решения задачи. По-прежнему возможно, что существуют другие симметричные объекты с р⁹ симметриями, которые могут скомпенсировать обнаруженное мною странное поведение, – и тогда гипотеза Хигмана останется справедливой. Поэтому на данный момент я не знаю, справедлива ли его гипотеза, а сам Хигман, к сожалению, умер, так и не узнав ответа на этот вопрос. Мне не терпится узнать его прежде, чем и моя конечная жизнь придет к своему концу, и именно вопросы такого рода побуждают меня заниматься математическими исследованиями.

Иногда, когда я блуждаю среди кажущихся бесконечными изгибов и поворотов своих исследований, я сомневаюсь, обладает ли мой мозг достаточными ресурсами для решения той задачи, над которой я работаю. Собственно говоря, при помощи математики можно доказать, что существуют математические задачи, превосходящие физические возможности человеческого мозга, который содержит 86 миллиардов нейронов, соединенных между собой более чем 100 триллионами синапсов.

Математика беспредельна. Она продолжается вечно. В отличие от шахмат, в которых, по оценкам, возможно около 10¹⁰⁵⁰ разных партий, число доказуемых математических утверждений бесконечно. В шахматах фигуры «съедают», партии выигрывают, и последовательности повторяются. В математике же не существует эндшпиля, из чего следует, что, даже если все мои 86 миллиардов нейронов будут возбуждаться с максимальной физически возможной скоростью, в течение всей своей жизни я смогу сделать лишь некоторое конечное число логических шагов и, таким образом, познать лишь некоторую конечную часть математики. Что, если для доказательства моей гипотезы PORC требуется больше логических шагов, чем я могу сделать за свою жизнь?

Даже если мы превратим всю Вселенную в один большой компьютер, возможный объем его знания все равно будет ограничен. В своей статье под названием «Вычислительная мощность Вселенной» Сет Ллойд подсчитал, что с момента Большого взрыва Вселенная не могла произвести более 10¹²⁰ операций с данными, максимальный объем которых составляет 10⁹⁰ битов. В любой момент времени Вселенная может знать лишь некоторую конечную часть математики. Вы можете спросить: «А что, собственно, вычисляет Вселенная?» На самом деле она вычисляет свою собственную динамическую эволюцию. И хотя эти числа огромны, они все же конечны. Это означает, что мы можем доказать путем вычислений, что в любой момент времени всегда будет нечто, чего мы не знаем.

Но оказывается, что в математике существует и еще более глубокий уровень неизвестного. Даже если бы у нас был компьютер бесконечной мощности и бесконечного быстродействия, и тогда оставались бы вещи, которых мы никогда не узнаем. Одна теорема, доказанная в ХХ в., открыла нам пугающую возможность того, что даже такой компьютер бесконечной мощности может никогда не узнать, справедлива ли моя гипотеза PORC. Эта так называемая теорема Гёделя о неполноте потрясла математику до основания. Возможно, эти гипотезы и справедливы, но мы никогда не сможем доказать их в рамках аксиоматической системы нашей математики. Гёдель доказал, что в рамках любой аксиоматической системы математики существуют математически истинные утверждения, истинность которых невозможно доказать в рамках той же аксиоматической системы. Математическое доказательство существования чего-то, что не может быть доказано, – математика за гранью.

Когда я узнал об этой теореме в университете, она сильно потрясла меня. Несмотря на физические ограничения моего собственного мозга или мозга Вселенной, я, по-видимому, вырос в уютном убеждении, что по меньшей мере теоретически где-то существует доказательство, которое покажет, истинна или ложна моя гипотеза PORC, истинна или ложна гипотеза Римана. Один из моих героев, венгерский математик Пал Эрдёш, всегда с нежностью отзывался о доказательствах из Книги – так Эрдёш называет свод, где Бог хранит самые изящные доказательства всех математических теорем. Задача математика состоит в открытии доказательств из Книги. Как пошутил Эрдёш на лекции, которую он читал в 1985 г., «не обязательно верить в Бога, но нужно верить в Книгу». Сам Эрдёш сомневался в существовании Бога и называл его «Верховным фашистом», который вечно прячет от него то носки, то венгерский паспорт. Но мне кажется, что большинство математиков было согласно с метафорой Книги. Однако из того доказательства, о котором я узнал на университетской лекции по математической логике, следовало, что в Книге не хватает некоторых страниц – страниц, которых нет даже у «Верховного фашиста».

Открытие существования математических утверждений, лежащих за пределами доказательств, было вызвано пониманием того, что одно из геометрических положений, которое Евклид использовал в качестве аксиомы, на самом деле не столь аксиоматично, как принято было думать.

Аксиома – это предпосылка или отправная точка любой последовательности логических рассуждений. В общем случае считается, что аксиома выражает некую самоочевидную истину, справедливость которой общепризнанна и не нуждается в доказательстве. Например, я верю, что если взять два числа, то в каком бы порядке я их ни складывал, я всегда получу один и тот же ответ. Если взять число 36 и прибавить к нему 43, ответ будет тем же, что и если взять 43 и прибавить 36. Можно спросить, откуда я знаю, что это всегда будет так. Может быть, если взять действительно большие количества объектов и сложить их, произойдет что-нибудь странное. Вот как работает математика: она производит дедуктивные выводы о числах, которые удовлетворяют этому правилу. Если тот способ, которым мы считаем объекты во Вселенной, дает какие-нибудь странные результаты, мы должны просто признать, что та математика, которую мы разработали на основе этой аксиомы, неприменима к тому, как ведут себя физические числа во Вселенной. Тогда нам нужно разработать новую теорию чисел, основанную на числах, удовлетворяющих другому фундаментальному набору аксиом.

Хотя многие из аксиом, которые Евклид использовал при развитии своей геометрической теории, казались самоочевидными истинами о геометрии Вселенной, одна из них постепенно стала вызывать у математиков все более серьезные подозрения.

Постулат о параллельных утверждает, что если имеются прямая и точка, не принадлежащая этой прямой, то через эту точку может быть проведена только одна прямая, параллельная первой прямой. Этот постулат несомненно кажется очевидным, если чертить геометрические фигуры на плоском листе. Эта аксиома – одна из тех, на которых основано евклидово доказательство того, что сумма углов треугольника равна 180°. Любая геометрия, в которой справедлив постулат о параллельных, безусловно порождает треугольники, обладающие этим свойством. Но открытые в XIX в. новые типы геометрий, в которых не существует параллельных прямых или могут быть проведены несколько параллельных прямых, привели математиков к пониманию того, что евклидова геометрия – всего лишь одна из множества разных возможных геометрий.

Например, если взять поверхность сферы с ее искривленной геометрией, то линии, лежащие на этой поверхности, будут не прямыми, а изогнутыми. Если взять две точки на поверхности Земли, то, как известно любому, летавшему через Атлантику, кратчайший путь между этими двумя точками не соответствует прямой, которую можно прочертить на плоской карте. Это связано с тем, что линия, соединяющая эти две точки, есть часть окружности, подобной меридиану, делящему сферу на две в точности равные половины. Действительно, если одна из наших точек совпадает с Северным или Южным полюсом, то интересующая нас линия будет отрезком меридиана. Все линии в этой геометрии являются отрезками меридианов, перемещаемыми по поверхности сферы так, чтобы они проходили через наши две точки. Их называют дугами большого круга. Но если теперь взять третью точку, не принадлежащую данному большому кругу, то через нее нельзя провести большой круг, который не пересекался бы с первым большим кругом. Итак, мы получили геометрию, в которой не существует параллельных линий. Соответственно, любое доказательство, основанное на постулате о параллельных, в такой новой геометрии может не быть истинным. Возьмем доказательство того, что сумма углов треугольника равна 180°. Это утверждение выведено в геометрии, в которой справедлив постулат о параллельных. Но в нашей сферической геометрии он не работает. И действительно, в этой геометрии существуют треугольники, сумма углов которых превышает 180°. Возьмем Северный полюс и две точки на экваторе. Два угла при экваторе уже дают в сумме 180°, так что сумма всех трех углов треугольника должна быть больше 180°.

Были открыты и другие геометрии, в которых через одну точку можно провести не одну, а много параллельных прямых. В таких геометриях, называемых гиперболическими, сумма углов треугольника меньше 180°. Эти открытия не отменили истинности никаких доказательств Евклида. Это прекрасный пример того, почему математические открытия лишь обогащают, а не перечеркивают знание, существовавшее до них. Но появление этих новых геометрий в начале XIX в. вызвало определенное беспокойство. Некоторые математики даже считали, что геометрия, не удовлетворяющая евклидовой аксиоме о параллельных прямых, должна содержать какое-то противоречие, которое в конце концов заставит отбросить ее как невозможную. Но дальнейшие исследования показали, что наличие каких-либо противоречий, присущих новым геометриям, означало бы, что противоречие существует и в основе геометрии Евклида.

Такая мысль казалась еретической. Евклидова геометрия прошла испытание временем и не обнаружила никаких противоречий за 2000 лет. Но погодите… что-то подобное мы уже слышали от естествоиспытателей. Уж математика-то должна быть способна доказать, что евклидова геометрия не порождает противоречий. Мы не можем просто считать, что, раз что-то успешно работало до этого момента, значит, все в порядке. Так делают естественники из лаборатории напротив. Мы, математики, должны быть способны доказать, что наша область свободна от противоречий.

Когда в конце XIX в. в математической теории множеств были получены странные результаты, которые, по-видимому, порождали неразрешимые парадоксы, математики стали относиться к такой необходимости доказательства отсутствия противоречий в своей области более серьезно. Многие из таких парадоксов придумал британский философ Бертран Рассел. Он поставил перед математическим сообществом задачу о множестве всех множеств, собственными элементами которых не являются они сами. Вопрос сводился к тому, является ли это новое множество элементом самого себя. Множество может быть его элементом, только если оно не содержит само себя в качестве элемента. Но, как только мы вводим это множество в число его же элементов, оно (конечно же) внезапно становится множеством, содержащим само себя в качестве элемента. Черт! Парадокс казался неразрешимым, и в то же время такая конструкция была не столь уж отлична от тех множеств, которыми математики могли заниматься всерьез.

Рассел предложил более прозаические, бытовые примеры такого рекурсивного парадокса. Например, он представил себе остров, на котором действует закон, согласно которому цирюльник должен брить всех тех, кто не бреется сам, – и не имеет права брить никого другого. Беда в том, что такой закон порождает парадокс: может ли цирюльник брить самого себя? Нет, так как ему можно брить только тех, кто не бреется сам. Но тогда он попадает в категорию тех, кого должен брить цирюльник. Снова черт! Цирюльник играет здесь роль того множества, которое пытался определить Рассел, – множества всех множеств, которые не являются элементами самих себя.

Из всех примеров таких парадоксов мне, наверное, больше всего нравится загадка об описании чисел. Представьте себе, что вы рассматриваете все числа, которые можно определить, используя менее 20 слов, взятых из «Оксфордского словаря английского языка». Например, число 1729 можно определить как «наименьшее число, которое может быть записано в виде суммы двух кубов двумя разными способами». Поскольку Оксфордский словарь содержит конечное количество слов, а мы можем использовать не более 20 слов, определить таким образом все числа невозможно, так как количество чисел бесконечно, а количество фраз, содержащих менее 20 слов, конечно. Поэтому должно существовать число, определяемое как «наименьшее число, которое невозможно определить, используя менее двадцати слов из Оксфордского словаря». Но погодите… Я ведь только что определил его, использовав менее 20 слов. Черт!

Естественный язык легко порождает парадоксальные утверждения. Простое соединение слов в предложение не гарантирует ни осмысленности, ни истинности. Но придуманное Расселом множество всех множеств, которые не содержат самих себя, вызывало тревогу тем, что оно было очень близко к тем объектам, математические определения которых нам могут потребоваться. В конце концов математики придумали, как обойти эту парадоксальную ситуацию, – для этого потребовалось уточнить интуитивное представление о множестве, но вся эта история оставила после себя неприятный привкус. Сколько еще неожиданностей таится в глубинах здания математики? Когда в 1900 г. великого немецкого математика Давида Гильберта попросили выступить на Международном математическом конгрессе, он решил очертить 23 величайшие нерешенные задачи, с которыми предстояло иметь дело математикам ХХ в. Доказательство отсутствия в математике противоречий было вторым пунктом в его списке.

В своей речи Гильберт решительно провозгласил главную, по мнению многих, мантру математики: «Эта убежденность в разрешимости любой математической задачи является мощным стимулом для работника. Мы слышим внутри себя вечный зов. Вот задача. Найди ее решение. Ты можешь найти его при помощи чистого разума, ибо в математике не существует “ignorabimus”». То есть в математике нет ничего такого, чего мы знать не можем. Смелое заявление.

Тем самым Гильберт давал отповедь разросшемуся в конце XIX в. движению, которое утверждало, что наши возможности понимания Вселенной ограниченны. В 1880 г., выступая в Берлинской академии наук, выдающийся физиолог Эмиль Дюбуа-Реймон очертил те семь загадок природы, которые, по его мнению, были непознаваемы, отнеся их к категории «ignoramus et ignorabimus». То, чего мы не знаем и никогда не будем знать.

В свете моих попыток понять, какие вопросы могут быть непознаваемыми, интересно сравнить мой список с семью загадками Дюбуа-Реймона:

1. Истинная природа вещества и силы.

2. Происхождение движения.

3. Происхождение жизни.

4. Кажущееся телеологическое устройство природы.

5. Происхождение простых ощущений.

6. Происхождение разума и языка.

7. Вопрос о свободе воли.

Дюбуа-Реймон считал, что пункты 1, 2 и 5 истинно трансцендентны. Первые два все еще в значительной степени составляют сущность вопросов, которые мы рассматривали на нескольких первых «рубежах». Телеологическое устройство природы относится к вопросу о том, почему Вселенная, по-видимому, так хорошо приспособлена для существования жизни, – и этот вопрос мучает нас до сих пор. Лучший из имеющихся у нас возможных ответов на него – это существование множественных вселенных. Последние три пункта были темой предыдущего «рубежа», на котором мы рассматривали пределы человеческого разума. Пожалуй, сколько-нибудь значительных успехов мы достигли только в разрешении загадки происхождения жизни. Несмотря на потрясающие успехи научного прогресса, достигнутые за последние сто лет, остальные шесть задач по-прежнему могут оказаться непознаваемыми, как и полагал Дюбуа-Реймон.

Но Гильберт не собирался включать математические утверждения в список загадок Дюбуа-Реймона. Тридцать лет спустя, 7 сентября 1930 г., когда Гильберт вернулся в свой родной Кенигсберг, чтобы получить звание его почетного гражданина, он закончил свою благодарственную речь следующим боевым кличем, обращенным к математикам:

Однако Гильберт не знал о поразительном заявлении, которое было сделано на конференции, проходившей в том же самом Кенигсберге за день до этой церемонии. «Ignorabimus» все-таки существует в математике. 25-летний австрийский логик по имени Курт Гёдель доказал невозможность доказать, что математика не содержит противоречий. Он пошел даже дальше. В аксиоматической системе любой математики существуют истинные утверждения о числах, истинность которых невозможно доказать в рамках этой же аксиоматической системы. Лозунг Гильберта – «Wir müssen wissen. Wir werden wissen» – в конце концов занял подобающее ему место на надгробии самого Гильберта. А математике пришлось иметь дело с тем фактом, что и в ней существуют загадки, которые мы никогда не сможем разгадать.

Название этого раздела истинно.

Именно из рекурсивных утверждений, подобных тому, которое я нашел в своей хлопушке на прошлое Рождество, Гёдель вывел свое обескураживающее доказательство ограниченности математики.

Хотя утверждения, сформулированные на естественном языке, могут порождать парадоксы, мы привыкли ожидать, что утверждение, сделанное о числах, может быть либо истинным, либо ложным. Гёделя заинтересовал вопрос о возможности использования рекурсивности в математических утверждениях. Поставленная Гильбертом задача уже содержала встроенный рекурсивный элемент: он хотел построить математически неопровержимое рассуждение, доказывающее, что математика не содержит противоречий. Эта задача уже требует рассмотрения математикой самой себя в поисках доказательства того, что в ней не могут внезапно появиться доказательства истинности двух взаимоисключающих утверждений.

Гёдель хотел показать, что в рамках любой системы аксиом теории чисел всегда будут существовать истинные утверждения о числах, которые невозможно доказать на основе этих аксиом. Стоит отметить, что можно попытаться определить, как работают эти числа, установив другую систему аксиом. Гильберт надеялся, что математики сумеют построить единую аксиоматическую систему, исходя из которой можно было бы доказать все математические истины.

Гёделю удалось разрушить эту надежду. Фокус, который использовал Гёдель, заключался в следующем: он разработал код, в рамках которого каждому осмысленному утверждению о числах был присвоен свой кодовый номер. Собственно, похожая идея используется в технологии, позволяющей мне печатать этот текст. Слова, которые я использую для изложения истории Гёделя, преобразуются в последовательности чисел, которые представляют те буквы, которые я печатаю. Например, в десятичном ASCII-представлении слово «Гёдель» изображается числом 195184228229235252. Достоинство кодировки, придуманной Гёделем, состоит в том, что она позволила математике говорить о самой себе.

В кодировке Гёделя каждая из аксиом, которые мы выбираем для выражения теории чисел, – те утверждения, из которых мы выводим математические теоремы, – получает свой собственный кодовый номер. Например, аксиома «Если А = В и В = С, то А = С» имеет некоторый кодовый номер. Но свой собственный кодовый номер также получает и каждое из утверждений, которые можно вывести из этих аксиом, например утверждение «Существует бесконечное количество простых чисел». Даже если утверждение ложно, например «17 – четное число», ему все равно присваивается кодовый номер.

Эти кодовые номера позволили Гёделю рассуждать о доказуемости того или иного утверждения в рамках данной системы на языке теории чисел. Основная идея состояла в том, чтобы получить такую кодировку, в которой кодовый номер доказуемого утверждения обладал бы делимостью на кодовые номера соответствующих аксиом. На самом деле система была более сложной, но такое упрощение поможет нам ее понять.

Теперь Гёдель мог говорить о доказуемости или недоказуемости того или иного утверждения на основе аксиом как о некотором свойстве чисел. Положение, согласно которому «утверждение о существовании бесконечного количества простых чисел может быть доказано, исходя из аксиом теории чисел», преобразовалось в утверждение «кодовый номер утверждения о существовании бесконечного количества простых чисел делится на кодовые номера аксиом теории чисел», то есть в чисто математическое утверждение о свойствах чисел, которое может быть либо истинным, либо ложным.

Держитесь покрепче, пока мы будем преодолевать все логические изгибы и повороты доказательства Гёделя. Гёдель решил рассмотреть следующее утверждение S: «Это утверждение недоказуемо». Утверждению S присвоен некий кодовый номер. Но, если проанализировать содержание утверждения S, оно попросту сводится к утверждению о наличии или отсутствии делимости кодового номера утверждения S на кодовые номера аксиом. Предположим, что аксиоматическая система теории чисел, которую мы анализируем, не порождает противоречий, как надеялся Гильберт.

В кодировке Гёделя S становится всего лишь утверждением о свойствах чисел. Кодовый номер S либо делится на кодовые номера аксиом, либо не делится. Это утверждение должно быть либо истинным, либо ложным. Оно не может одновременно быть и истинным, и ложным, так как это противоречило бы нашему предположению об отсутствии противоречий в данной системе.

Предположим, что доказательство утверждения S на основе аксиом теории чисел существует. Из этого следует, что кодовый номер S делится на кодовые номера некоторых аксиом. Но доказуемое утверждение истинно. Однако, если проанализировать содержание утверждения S, мы увидим, что оно означает, что кодовый номер S не делится на номера аксиом. Противоречие. Но мы предположили, что математика не содержит противоречий. В отличие от парадокса из моей рождественской хлопушки из этой логической загадки должен существовать какой-то выход.

Чтобы выйти из этого тупика, следует понять, что наше исходное предположение было ложным: мы не можем доказать истинность утверждения S, исходя из аксиом теории чисел. Но именно это и утверждает S. То есть утверждение S истинно. Мы доказали, что предложенное Гёделем утверждение S – истинное утверждение, недоказуемое с использованием этих аксиом.

Это доказательство может напомнить вам, как мы доказали, что квадратный корень из 2 есть иррациональное число. Сначала предположим, что это не так. Это предположение приводит к противоречию. Значит, корень из двух все же должен быть иррациональным. Доказательство обоих результатов основано на том важном допущении, что аксиомы теории чисел не порождают противоречий. Одно из наиболее интересных следствий из доказательства Гёделя состоит в том, что математику нельзя спасти, введя в нее одно из таких недоказуемых утверждений в качестве аксиомы. Можно подумать, что, раз утверждение S истинно, но недоказуемо, почему бы не принять его за аксиому – и тогда, может быть, все истинные утверждения окажутся доказуемыми? Доказательство Гёделя демонстрирует, что, сколько бы новых аксиом мы ни вводили в систему, в ней всегда останутся недоказуемые истинные утверждения.

Если вы чувствуете легкое головокружение от того логического танца, в который увлек нас Гёдель, не волнуйтесь. Хотя я изучал эту теорему много раз, к концу доказательства у меня всегда несколько кружится голова – настолько поразительны его следствия. Гёдель представил математическое доказательство того, что в любой непротиворечивой аксиоматической системе теории чисел существуют истинные утверждения о свойствах чисел, справедливость которых невозможно доказать в рамках данной системы, – математическое доказательство ограниченности математики. Интересно отметить, что непознаваемо тут не само утверждение S. Собственно говоря, мы доказали его истинность. Дело в том, что для этого нам пришлось выйти за пределы данной конкретной аксиоматической системы математики, и тем самым мы продемонстрировали ее ограниченность. Именно это и продемонстрировал Гёдель – что истинность этого утверждения не может быть доказана в рамках данной системы.

Это уже достаточно обескураживающее открытие Гёделя, известное под названием первой теоремы Гёделя о неполноте, уничтожило надежду Гильберта на математическое доказательство отсутствия в математике противоречий. Гёдель доказал, что утверждение «Это утверждение недоказуемо» истинно в предположении о том, что математика не содержит противоречий. Если отсутствие противоречий можно доказать математически, то это обстоятельство можно использовать для доказательства в рамках такой математики, что утверждение «Это утверждение недоказуемо» истинно. Но при этом как раз и возникает противоречие, поскольку само это утверждение утверждает, что оно недоказуемо. Поэтому любое доказательство отсутствия в математике противоречий неизбежно приводит к противоречию. Мы снова вернулись к нашим рекурсивным утверждениям. Единственный выход из этой ситуации заключается в признании невозможности математического доказательства того, что математика лишена противоречий. В этом состоит вторая теорема Гёделя о неполноте. К ужасу Гильберта, она обнаружила «ignorabimus» в самом сердце математики.

Однако математики считают, что математика не содержит противоречий. Если бы в ней были противоречия, как бы мы смогли зайти так далеко без обрушения всего ее здания? Мы называем теорию, не содержащую противоречий, непротиворечивой. Французский математик Андре Вейль сформулировал потрясающие последствия достижений Гёделя следующим образом: «Бог существует, поскольку математика непротиворечива, а дьявол существует, поскольку мы не можем этого доказать».

Значат ли открытия Гёделя, что математика может быть опровергнута так же, как и любая другая научная теория? Возможно, мы случайно обнаружили правильную модель, но, как и в случае моделей Вселенной или элементарных частиц, мы не можем быть уверены, что в один прекрасный момент она не развалится на кусочки под весом новых данных.

Некоторые философы находили нечто привлекательное в том факте, что, хотя мы не можем доказать истинность утверждения S Гёделя в рамках аксиоматической системы теории чисел, мы по меньшей мере смогли доказать, что оно истинно, выйдя за пределы этой системы. Казалось, что из этого следует, что человеческий мозг – нечто большее, чем механизированная вычислительная машина для математического анализа мира. В 1959 г. философ Джон Лукас выступил в Оксфордском философском обществе с докладом под названием «Разум, машина и Гёдель», в котором он утверждал, что если мы построим модель разума в виде машины, следующей аксиомам и логическим правилам арифметики, то такая машина, разрабатывая доказательства, в какой-то момент наткнется на фразу «Это утверждение недоказуемо» и будет до скончания времен пытаться доказать или опровергнуть это утверждение. В то же время человек может увидеть, что оно неразрешимо, поняв его смысл. «Таким образом, машина все еще не будет адекватной моделью разума. […] разум, будучи “живым”, может всегда пойти на шаг дальше любой формализованной, окостеневшей, мертвой системы».

Это рассуждение выглядело очень привлекательно. Кто не хотел бы верить, что мы, люди, – нечто большее, чем простые вычислительные системы, чем приложения, установленные в неких биологических устройствах? Роджер Пенроуз использовал рассуждение Лукаса в своем недавнем исследовании сознания в качестве основы для своего убеждения в том, что для понимания того, что делает разум сознательным, нам необходима новая физика. Но, хотя мы действительно подтверждаем истинность утверждения «Это утверждение недоказуемо» путем выхода за пределы системы, это также требует большого допущения, а именно, что система, в рамках которой мы пытаемся доказать истинность этого утверждения Гёделя, сама не содержит противоречий. А суть второй теоремы Гёделя о неполноте состоит в том, что мы не можем этого доказать.

Утверждения, подобные созданным Гёделем, истинные, но недоказуемые, могут показаться с математической точки зрения несколько эзотерическими. Не может же быть так, чтобы действительно интересные утверждения о свойствах чисел – гипотеза Римана, гипотеза Гольдбаха, гипотеза PORC – были недоказуемы? Надежда на то, что доказательству не подлежат лишь хитроумные утверждения Гёделя, оказалась ложной. В 1977 г. математики Джефф Пэрис и Лео Харрингтон предъявили вполне настоящее математическое утверждение о свойствах чисел и сумели показать, что оно истинно, но недоказуемо в рамках классической аксиоматики теории чисел. Но в следующей части этой главы мы увидим, что, пытаясь справиться с идеей бесконечности, математики открыли не только недоказуемость некоторых утверждений, но и невозможность определить, истинны они или ложны.

Если вы прочитали «Рубеж третий» и эту главу, вы должны быть готовы к восприятию еще одного анекдота из моих парадоксальных рождественских хлопушек. Единственное, что вам еще нужно знать, – это что американский лингвист и философ Ноам Хомский проводит различие между языковой способностью (лингвистическими знаниями, которыми обладает культура) и языковым поведением (тем, как язык используется в общении). Так вот, анекдот: