Книга: О том, чего мы не можем знать. Путешествие к рубежам знаний
Назад: 5
Дальше: Рубеж четвертый: Бумажная Вселенная
6
Как удивительны все эти перемены! Не знаешь, что с тобой будет в следующий миг.Льюис Кэрролл.
Приключения Алисы в Стране чудес
Должен сказать, что меня сильно беспокоят противоречия между квантовым миром и здравым смыслом. Кажется, так и должно быть. Нильс Бор, один из основателей квантовой механики, говорил: «Если квантовая физика вас не шокирует, значит, вы ее еще не поняли».
Ричард Фейнман пошел еще дальше: он заявил, что «никто не понимает квантовой физики». Когда ему было за шестьдесят, он признал в программной лекции на конференции по вычислительной физике: «Позвольте мне сразу сказать, что нам всегда (только это секрет, закройте скорее дверь!) – нам всегда было очень трудно понять то видение мира, которое дает квантовая механика. Меня лично оно до сих пор нервирует».
Мой внутренний математик мечтает о каком-нибудь детерминистическом механизме, который рассказал бы мне, когда уран в моей банке испустит следующую частицу. Но вероятностный характер квантовой физики чрезвычайно сильно ограничивает нашу способность узнать, что произойдет дальше. Уравнения Ньютона открыли перед нами увлекательнейшие перспективы: зная импульс и положение частицы, мы можем полностью определить ее поведение в будущем при помощи уравнений движения. А если повторить тот же опыт с другой частицей, расположенной в той же точке и имеющей такой же импульс, то ее траектория совпадет с траекторией первой частицы.
Но в 1927 г. Гейзенберг совершил открытие, которое практически уничтожило такую надежду на познание будущего. Он выяснил, что выражение «знать импульс и положение частицы в одно и то же время», по сути дела, не имеет смысла. Оказалось, что между знанием положения частицы и знанием ее импульса существует некая жесткая связь. Если измерять положение частицы, увеличивая точность измерений, то оказывается, что ее импульс может иметь целый диапазон возможных значений. В этом и состоит знаменитый принцип неопределенности Гейзенберга, ставший, вероятно, самым серьезным препятствием для нашего познания. Как мы увидим далее, именно принцип неопределенности Гейзенберга виноват в том, что уран, лежащий у меня на столе, испускает частицы случайным образом.
То, как важно быть готовым пересмотреть видение мира в свете этого нового открытия, хорошо выразил сам Гейзенберг: «В любом случае, где мы переходим от познанного к непознанному, мы надеемся нечто понять, но одновременно, пожалуй, необходимо при этом подчеркнуть новое значение слова “понимать”».
Квантовая физика не столько дает ответы на старые вопросы, сколько подвергает сомнению те вопросы, которые мы имеем право задавать.
Квантовые ковры
Вот к чему сводится суть открытия Гейзенберга. Возьмем одну из частиц внутри моего куска урана. Если мы знаем, что эта частица пребывает в состоянии покоя – не движется, – то оказывается, что мы не можем знать, где она находится. То есть если проверить ее местоположение, есть шанс обнаружить ее в любой точке Вселенной. Напротив, если попытаться точно определить, где эта частица находится, мы внезапно теряем возможность определения того, как она движется. Частица, которая казалась нам покоящейся, неожиданно оказывается движущейся в произвольном направлении.
Эта идея кажется абсолютно безумной. Подбросив игральную кость в воздух и внимательно следя за ее падением на стол, я не ожидаю, что мое знание положения кости внезапно заставит ее улететь в совершенно новом направлении. Но такое интуитивное представление справедливо только в отношении объектов с большой массой. Если масса мала – например в случае электрона, – то именно так все и происходит. Если определить положение электрона с точностью до радиуса атома, его скорость может изменяться на величину, составляющую до 1000 км/с, причем в любом направлении.
Это похоже на попытки расстелить некий странный квантовый ковер: каждый раз, как мы фиксируем край ковра, соответствующий положению, его импульсный край задирается; стоит нам зафиксировать импульсный край, как другой край ковра уходит со своего места.
Чтобы разобраться в этой упругой связи между положением и импульсом, вернемся к нашему щелевому экрану. Мы изучали странное поведение частицы, направленной на экран, в котором прорезаны две щели. А вот странные отношения между положением и импульсом проявляются в поведении частицы, пролетающей через одиночную щель. Мы уже отмечали, что при пролете частиц через одиночную щель возникает некоторая диффузия. А почему, собственно, один электрон, пролетающий через щель, вообще должен отклоняться? Если электрон – точечная частица, почему же он не пролетает прямо через щель? Как можно объяснить распределение его возможных положений после пролета через щель? Наблюдаемую в этом случае диффузию объясняет именно балансирование между знанием положения и знанием импульса.
Установим источник электронов на большом расстоянии от экрана: тогда, если электрон пролетает через щель, он заведомо не может сместиться в направлении, перпендикулярном щели. Это означает, что, если частица попадает в щель, мы знаем, что ее импульс в этом направлении равен нулю. То есть его значение нам известно точно.
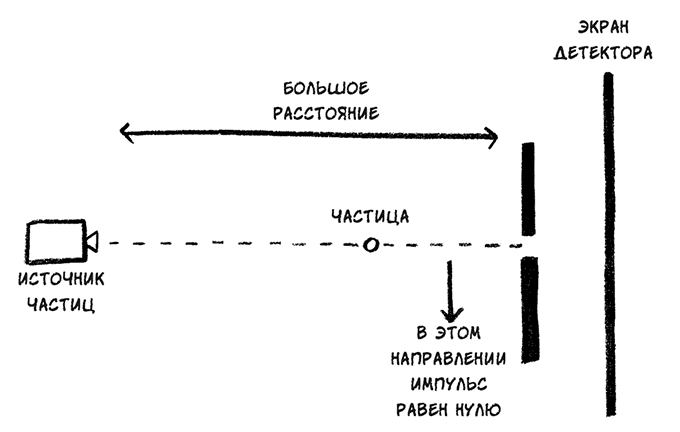
Если считать электрон точечной частицей, то он либо пролетает через щель, не задевая экрана, либо не пролетает. Если он пролетает через щель, мы получаем информацию о его положении, точность которой определяется шириной щели. То есть теперь можно предсказать, в какое место детектора он попадет. Поскольку до попадания электрона в щель импульс в направлении, перпендикулярном ей, был нулевым, электрон должен попасть в участок детектора, ширина которого точно равна ширине щели. Почему же при пропускании через щель все большего числа электронов мы получаем ту же диффузионную картину, которая возникает при попадании волн на пластину детектора? Почему не все электроны прилетают на участок, ширина которого равна ширине щели?
Принцип неопределенности Гейзенберга утверждает, что любое измерение, касающееся точного определения положения электрона, порождает неопределенность значения его импульса. Так, например, если электрон пролетел через щель, то его положение известно нам с точностью, определенной шириной щели. По мере уменьшения ширины щели уменьшается и погрешность определения положения. Но диффузионный рисунок становится при этом все шире и шире. Почему? Потому, что это влияет на величину импульса. Если при подлете к щели импульс в направлении, перпендикулярном ей, был равен нулю, то после вылета электрона из щели его положение определено более точно, а его импульс становится неопределенным. Мы зафиксировали край квантового ковра, отвечающий за положение, и его импульсный край от этого задрался.
Очень странная ситуация. Более того, нельзя вычислить заранее, каким именно будет воздействие на импульс. Его можно только измерить впоследствии. Нам доступен только диапазон возможных значений, в пределах которого будет найден импульс при наблюдении. К тому же, если повторить тот же опыт, оказывается, что импульс не определяется условиями эксперимента. Для определения возможного значения импульса имеется только вероятностный механизм.
Численное выражение неопределенности
Принцип неопределенности Гейзенберга дает не просто расплывчатое утверждение общего характера, но численную меру потери знания. Если положение электрона известно с высокой точностью, то его импульс в момент вылета из щели не будет точно равен нулю, а может статистически варьироваться вокруг равного нулю среднего значения. Мы не можем знать, какое значение мы получим при измерении импульса, так как оно все еще неопределенно, но знаем, что возможные значения импульса должны быть статистически распределены по обе стороны от нулевого среднего значения. Можно измерить ширину такого распределения, которую называют стандартным отклонением импульса и обозначают Δp. Эта величина является статистической мерой разброса возможных значений. Чем больше этот разброс, тем больше значение Δp и тем более неопределенно значение импульса.
После того как в 1927 г. появилась исходная статья Гейзенберга, описывающая эту странную обратную связь между знанием положения и знанием импульса, Эрл Кеннард, а позднее Говард Робертсон нашли математическое выражение такого балансирования знаний. Если стандартное отклонение разброса возможных положений равно Δx, а стандартное отклонение разброса возможных значений импульса – Δp, то эти две величины удовлетворяют следующему неравенству:
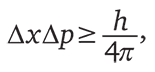
где h – постоянная Планка, то же число, которое встречалось нам в объяснении энергии фотона. Эта формула утверждает, что если погрешность измерения положения, равная Δx, уменьшается, то для сохранения справедливости соотношения должна увеличиться погрешность измерения импульса, равная Δp. Математическим следствием из квантовой физики является тот факт, что чем точнее полученное знание о положении частицы, тем более возрастает диапазон ее возможного распределения импульса. Именно это и происходит при пролете электрона через одиночную щель.
Взаимосвязанная природа этих двух свойств вытекает из значимости порядка, в котором проводятся измерения. Акты измерения положения и импульса описываются математически двумя операциями, которые, будучи произведены в разных последовательностях, дают разные результаты. Эту идею можно проиллюстрировать при помощи все той же игральной кости. Предположим, кость лежит на столе так, что верхней оказывается грань с единицей, как показано на рисунке. Повернем кубик на четверть оборота вокруг вертикальной оси, проходящей через верхнюю грань, а затем – на четверть оборота вокруг горизонтальной оси, проходящей вокруг одной из боковых граней. Теперь на верхней грани оказалась пятерка. Но если вернуть кость в исходное положение и повторить те же движения, но в обратном порядке, результат получится иным. Теперь верхней оказывается грань с четверкой.
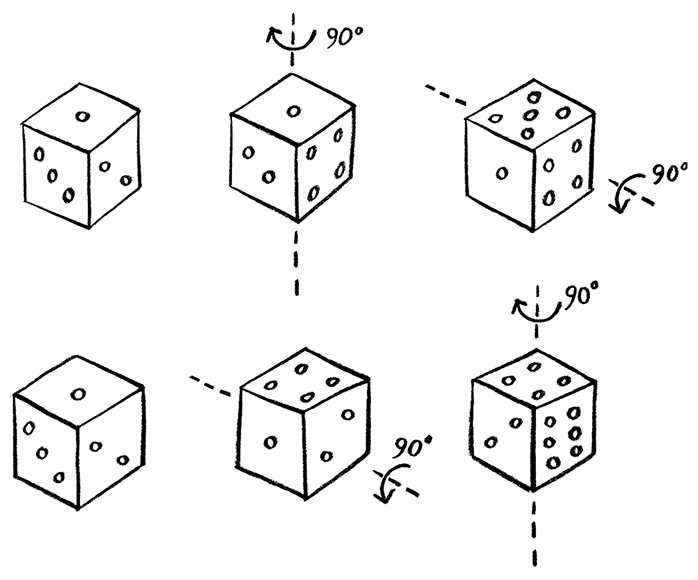
Любые измерения, обладающие этим свойством – что порядок, в котором производят соответствующие им математические операции, имеет значение, – порождают принцип неопределенности. Он попросту является математическим следствием свойства, называемого некоммутативностью.
Именно математика, лежащая в основе квантовой физики, в значительной степени ответственна за ее противоречие здравому смыслу. Когда я зарываюсь в книги и статьи по квантовой физике, мне кажется, что я вхожу в лабиринт. Перед началом путешествия мне казалось, что я знаю, где нахожусь. Затем я стал прокладывать свой логический маршрут через изгибы и повороты лабиринта, используя свои математические навыки. Мне приходится полагаться на математику, потому что стены лабиринта так высоки, что не позволяют мне даже догадываться о том, какой мир лежит за ними. Но когда математика выводит меня на другую сторону и я пытаюсь разобраться, куда я попал, окружающая меня местность выглядит совершенно непохожей на то место, с которого я начал свой путь.
С математикой-то все в порядке: трудность представляет интерпретация результатов, которые она выдает. Создается такое впечатление, что у меня нет языка, который позволил бы перевести то, что эта математика сообщает нам о реальности. Может быть, мои затруднения не реальны, а порождены ограничениями, которые накладывают старый язык и старые теории. Квантовая физика – это кроличья нора, и, упав в нее, мы должны кардинально изменить свою точку зрения и сформулировать новый язык, который позволил бы нам уверенно путешествовать по этому зазеркальному миру. И, нравится нам это или нет, этот язык – математика.
Но можно ли доверять математике? Выведенное из теории поведение, предсказанное математикой принципа неопределенности Гейзенберга, было подтверждено экспериментально. Американский физик Клиффорд Шалл описывает в статье, опубликованной в 1969 г., результаты обстрела нейтронами щели с уменьшающейся шириной. Как и предсказывала теория, увеличение точности определения положения нейтронов, обеспечиваемое уменьшением ширины щели, приводило к росту разброса возможных значений их импульса. И, когда нейтроны долетали до пластины детектора, наблюдалось распределение, стандартное отклонение которого точно соответствовало предсказаниям уравнения принципа неопределенности Гейзенберга.
Простой акт более точного определения положения нейтрона привел к потенциальному изменению его импульса. Принцип неопределенности Гейзенберга выражает в виде уравнения тот факт, что мы никогда не сможем знать всего. Увеличение знания неизбежно достается нам ценой соответствующего увеличения незнания.
Получая более точную информацию об одних величинах, мы теряем определенность других. Но такая неопределенность может иметь неожиданные последствия. Если заключить электрон внутри очень маленькой коробочки, положение такого электрона будет известно с высокой точностью. Но в результате этого значения его импульсы будут распределены в чрезвычайно широком диапазоне. При попытке измерения импульса происходит редукция волновой функции, в результате которой импульс может получить одно из множества разных значений.
Можно предположить, что, измерив импульс, мы сможем узнать и положение, и импульс. Но на самом деле такое измерение делает положение неопределенным. Места возможного нахождения электрона распределяются по пространству в такой степени, что мы получаем так называемый квантовый туннельный эффект, и в результате частица, которую мы считали заключенной в коробке, неожиданно оказывается вне ее. Именно этот эффект является причиной испускания альфа-частиц ураном, лежащим у меня на столе.
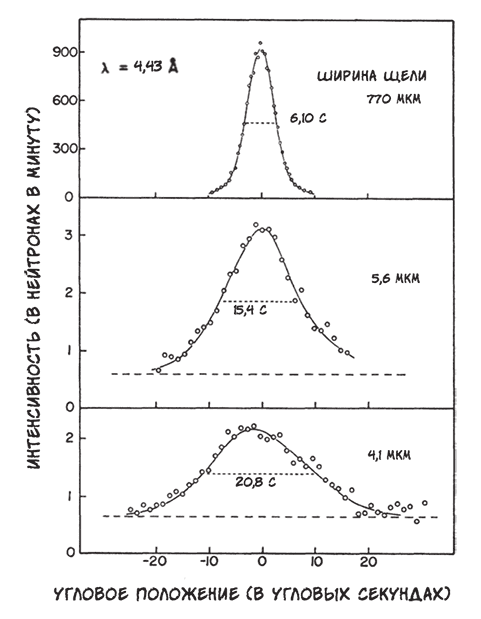
Опыт Клиффорда Шалла подтвердил, что уменьшение ширины щели приводит к увеличению статистического разброса положений нейтронов
Альфа-частица является частью ядра урана и состоит из двух протонов и двух нейтронов. Ядро как бы представляет собой маленькую коробочку, в которой содержатся альфа-частицы. В общем случае такие частицы не имеют энергии, достаточной для преодоления сил, удерживающих их в ядре. Поскольку их скорость и, следовательно, импульс ограничены таким образом, их импульс известен нам с высокой точностью. Но тогда, в соответствии с принципом неопределенности Гейзенберга, положение этих частиц определено не столь точно. Существует даже вероятность того, что это положение может находиться вне ядра и в таком случае частицы могут вылетать из него. Такая неопределенность положения и является причиной излучения урана.
Пределы знания на малом масштабе
Принцип неопределенности не только объясняет непредсказуемость моей банки урана, но и устанавливает пределы знания, которое я могу получить, забираясь все глубже и глубже внутрь игральной кости, чтобы посмотреть, что там происходит.
Если пытаться точно измерить координаты одного из электронов внутри кости, то за уменьшение погрешности определения координат придется заплатить соответствующей неопределенностью импульса и, следовательно, энергии. Соотношение неопределенности Гейзенберга дает математическое выражение этого баланса. Но есть и еще одно обстоятельство. Поскольку энергия и масса связаны уравнением Эйнштейна E = mc2, то при достаточно высокой энергии может произойти рождение новых частиц. Затруднение состоит в том, что, если попытки определения положения частицы приводят к образованию новых частиц, это существенно усложняет исследование положения исходной частицы. Характерный масштаб, на котором возникает такое осложнение, называется комптоновской длиной волны частицы. Для электрона она составляет около 4 · 10–13 м.
При переходе к еще меньшим расстояниям неопределенность ситуации становится все сильнее. В некоторой точке неопределенность энергии возрастает настолько, что соответствующая масса становится достаточно большой для возникновения черной дыры. Как мы увидим на пятом «рубеже», черная дыра по самой своей природе удерживает в себе любую информацию в пределах определенного расстояния от центра дыры и препятствует ее высвобождению.
Это означает, что из принципа неопределенности вытекает существование встроенного предела, ограничивающего возможности исследования природы. Оказывается, что начиная с некоторого масштаба мы не можем получить дальнейшего доступа вглубь происходящего. Масштаб этот очень мал. Он составляет порядка 1,616 · 10–35 м и называется планковской длиной. Это чрезвычайно мало. Если увеличить точку, стоящую в конце этого предложения, до размеров наблюдаемой Вселенной, то планковская длина будет сопоставима с размерами точки до такого увеличения.
На предыдущем «рубеже» мы дошли до точки, после которой не могли далее делить материю; сейчас мы дошли до точки, после которой не можем далее делить пространство. Бред какой-то. Почему мы не можем говорить о точке, расположенной посередине между двумя точками, разделенными планковской длиной? Это вполне возможно с математической точки зрения, но, по-видимому, не с физической. Физика утверждает, что различить такие точки невозможно.
Из этого следует, что пространство на этом масштабе выглядит разрозненным, зернистым, дискретным – а вовсе не непрерывным, как полагал Ньютон. В таком представлении пространство оказывается скорее цифровым, чем аналоговым. А из этого, в свою очередь, следует, что фракталы, о которых мы говорили на первом «рубеже», не могут иметь какой-либо физической реальности в квантовой физике. Фрактал должен обладать бесконечной сложностью на любом масштабе, но квантовая физика останавливает увеличение масштаба на уровне планковской длины. Значит ли это, что фракталы первого «рубежа» существуют только в математическом воображении? Кажется, что квантовая физика и теория хаоса несовместимы друг с другом. Возможно, квантовая физика способна подавлять хаотические системы.
Следует оговориться, что такая невозможность проникнуть за планковскую длину существует в современной теории. Именно на этом масштабе перестают как следует работать квантовая физика и общая теория относительности. Нам нужна новая теория, и именно с этим связаны все те усилия, которые прилагают к разработке квантовой гравитации и теории струн. Например, в теории струн частицы представляют собой не точки, а конечные струны, длина которых имеет порядок планковской длины, причем разные частицы вибрируют с разной частотой. Существуют ли действующие на таком масштабе правила, которые позволяли бы извлекать информацию на еще более мелких масштабах?
Наблюдение есть творение
Принцип неопределенности неоднократно пытались представить следствием влияния на систему акта наблюдения. Чтобы узнать, где находится частица, на нее нужно направить фотон, который сталкивается с частицей и передает ей импульс неизвестной величины. Таким объяснениям не следует доверять. Они привлекательны, но обманчивы. В приведенном выше примере пролета электрона через одиночную щель для изменения импульса электрона не требуется никаких фотонов. Оно происходит исключительно в результате пролета электрона через щель, который дает нам новую информацию о положении этой частицы, а это вызывает соответствующую потерю знания ее импульса. Никакого непосредственного взаимодействия, толкающего частицу в ту или иную сторону, тут нет.
Такое обманчивое описание столкновения частицы со световыми фотонами, по-видимому, восходит к исходной статье Гейзенберга. Он должен был включить в нее это описание, чтобы убедить скептически настроенных редакторов напечатать его статью.
На самом деле принцип неопределенности Гейзенберга ставит под сомнение смысл высказывания об одновременном наличии у электрона положения и импульса. Выражений вроде «знать положение и импульс частицы» следует избегать – они не имеют осмысленного эмпирического содержания.
Возможно, принцип неопределенности представляет собой нечто большее, чем просто выражение того, чего мы не можем знать. Он выражает скорее пределы определения некоей концепции. В этом смысле он согласуется с описанием электрона при помощи волновой функции, которое вообще не предполагает, что электрон имеет какое-либо точное положение в пространстве до наблюдения. Сам Гейзенберг сформулировал следующую точку зрения на головоломку о том, что представляет собой реальность:
Я считаю, что возникновение классической «траектории» можно четко определить следующим образом: «траектория» возникает только благодаря тому, что мы ее наблюдаем.
Что на самом деле говорит нам принцип неопределенности Гейзенберга – серьезный вопрос. Означает ли он, что мы никаким образом не можем узнать точное положение и импульс электрона в один и тот же момент? Или же что они вообще не существуют? Дело не в том, что мы не можем их узнать, а в том, что эти параметры вообще не имеет смысла определять для электрона. Наблюдение есть творение.
Некоторое время я никак не мог поверить, что такие фундаментальные свойства, как положение и импульс, возникают, только когда их измеряют. Импульс электрона может измениться после его вылета из узкой щели, но должен же он иметь какое-то точное значение даже до того, как мы его измерим? Я могу согласиться с тем, что мы не знаем этого значения, пока не определим этот импульс при помощи измерительных приборов, но такого, что остается неизвестным, пока не будет измерено, вообще на свете немало. Однако квантовая физика уверяет нас, что такая вера в существование точного значения до измерения ошибочна. Свойства частицы создаются именно нашим взаимодействием с системой. Возможно ли, чтобы наш акт измерения создавал реальность этой частицы?
Я не одинок в своих сомнениях. Например, Эйнштейн был одним из тех, кто пытался оспорить идею о том, что параметры, подобные положению и импульсу, остаются неопределенными до тех пор, пока они не будут наблюдаться. Конечно, говорил он, когда частица летит в вакууме, такие свойства на самом деле должны иметь явные значения. Мы можем не знать, чему они равны, или располагать приборами или математическими методами для их определения, но они в любом случае существуют, они в любом случае осмысленны. Не следует смешивать эпистемологию с онтологией. Даже если мы не можем одновременно знать положение и импульс (эпистемология), это не значит, что они не существуют (онтология).
Однако мне пришлось расстаться с такой интуитивной верой в существование объектов до измерения, когда я прочитал о замечательной теореме Белла, которую открыл в 1964 г. североирландский физик Джон Белл. Его теорема объяснила, почему некоторые свойства частицы не могут существовать до того, как они будут измерены. Если попытаться заставить их существовать до измерения, приходишь к противоречию. Как показал Белл, поскольку система не знает заранее, какие именно измерения мы решим произвести, то присвоить свойствам значения, которые учли бы все возможные измерения, невозможно без получения результатов, противоречащих известным нам теоретическим и экспериментальным данным. Это все равно что решать головоломку судоку, которая содержит ошибку. Как ни старайся вписать во все клетки правильные значения, все равно получается столбец или строка, содержащие два одинаковых числа.
Поскольку с математической точки зрения теорема Белла совершенно неопровержима, мне пришлось согласиться с тем, что измерение, по-видимому, действительно создает свойства частицы. Но у меня все еще остаются сильные сомнения в том, что результат акта измерения столь случаен, как уверяет нас современная теория.
Скрытая машина
Теорема Белла означает, что следует смириться с неизбежным и признать, что квантовая игральная кость не брошена, пока на нее никто не смотрит. Только измерение останавливает качение кости и заставляет ее решить, какой стороной она выпала. Но так ли случаен результат, как предполагает квантовая физика? Я знаю, что поведение моей игральной кости из казино на самом деле не вполне случайно. То, какой стороной падает кость, в конечном счете определяет некий физический механизм. Я подозреваю, что дело может обстоять таким же образом и с излучением моей банки урана.
Признаюсь, что у меня есть тайное подозрение, что квантовая физика – лишь временный мостик на пути к более полному пониманию поведения фундаментальных частиц. Наверняка, как и в случае игральной кости, должен существовать какой-то механизм, решающий, когда кусок радиоактивного урана испустит очередную альфа-частицу или в какой участок детектора попадет электрон, пролетевший через двойную щель.
Эйнштейн явно придерживался того же мнения, что и выражает его знаменитое высказывание:
Квантовая механика, несомненно, впечатляет. Но внутренний голос говорит мне, что это еще не окончательная истина. Эта теория дает нам многое, но почти ни на шаг не приближает нас к тайне Всевышнего. Во всяком случае, я убежден, что в кости Он не играет.
Он считал, что за этой завесой, которая кажется нам непроницаемой, должна скрываться какая-то объективная реальность. Он верил, что должны существовать еще меньшие шестеренки, определяющие результаты измерений, даже если мы и не в состоянии до них добраться.
Повторюсь, что в этом отношении я согласен с Эйнштейном. Я уверен, что существует какой-то внутренний механизм – даже если он пока что нам и неизвестен, – который определяет результат, взаимодействуя с измерительным прибором. Я готов признать, что такой механизм может производить результаты, соответствующие модели случайности, так же как моя игральная кость. Но что-то, определяющее эти результаты, должно существовать. Может быть, в частицах находящегося в моей банке урана установлены микроскопические часы: если в момент измерения секундная стрелка находится между 0 и 30, то уран испускает излучение; если стрелка находится между 30 и 60, то излучение не регистрируется.
Если такие внутренние часы существуют, то, как мы увидим далее, они должны представлять собой в высшей степени замечательный механизм, причем противоречащий другому аспекту здравого смысла. Мне кажется, что такой механизм должен располагаться вблизи банки с ураном. Он может быть внутри частиц, содержащихся в уране, и быть так мал, что мы не сможем его увидеть. Возможно, мы никогда не сумеем его исследовать. Проблема заключается в том, что сценарий, впервые придуманный Эйнштейном и его коллегами Борисом Подольским и Натаном Розеном, показал, что, если бы такой механизм существовал, его можно было бы переместить хоть на другой край Вселенной и расположить сколь угодно далеко от моего куска урана. Возможно, это и так, но представляется весьма удивительным, что если нечто подобное скрытым часам, которые принимают решение о моменте испускания ураном альфа-частицы, существует, то оно представляет собой механизм, охватывающий всю Вселенную.
Сценарий, который предложили Эйнштейн, Подольский и Розен, использует идею так называемой «квантовой зацепленности». Можно создать две частицы, свойства которых коррелируют в том смысле, что измерение свойств одной из частиц заставляет вторую соответствовать этим результатам. В качестве аналога можно представить себе ситуацию с двумя игральными костями, устроенными так, что, когда на одной из них выпадает шестерка, вторая должна упасть таким же образом. Изготовить пару таких взаимно зацепленных кубиков было бы довольно трудно – именно потому, что механизм, определяющий, как выпадет кость, управляется ее взаимодействием с локальными условиями и кажется невозможным понять, как он может управлять поведением второй кости. Однако в квантовой физике создание таких зацепленных и взаимозависимых частиц вполне возможно, но свойства скрытого механизма, определяющие поведение таких зацепленных частиц в случае измерения, чрезвычайно странны.
Чтобы продемонстрировать удивительную нелокальную природу такого механизма – если он вообще существует, – предположим, что две зацепленные квантовые кости отправлены на противоположные концы Вселенной. При измерении первой из квантовых костей она должна решить, какая грань на ней выпала, и это решение мгновенно определяет, какая грань выпала на второй кости, находящейся на другом краю Вселенной. Некоторых ученых, в том числе и Эйнштейна, сильно беспокоило такое «пугающее» дистанционное действие. Эйнштейн считал, что результат броска кости может быть каким-то образом определен заранее, до отправления частиц на противоположные концы Вселенной. Но это было до того, как Белл доказал свою теорему, которая утверждает, что установить свойства квантовой частицы до измерения невозможно. Не забываем: измерение есть творение.
Наибольшие трудности вызывает понимание того, как такое творение, произведенное на одном конце Вселенной, может мгновенно создать новое состояние второй частицы, находящееся на противоположном краю. Если тут действует какой-то внутренний механизм, определяющий результат измерения для второй частицы, то такой механизм воздействует на то, что происходит на другом краю Вселенной. Он не может быть локализован. Такой механизм просто не может быть вставлен внутрь частицы.
Эйнштейн и раньше высказывал озабоченность «пугающим действием на расстоянии», говоря об опыте с двойной щелью. Как фотопластинка может знать, что она не должна регистрировать электрон в одной точке, если он должен быть обнаружен в другой? Как кажется, происходит мгновенное редуцирование волновой функции, причем какой-либо каскадный эффект из точки наблюдения по остальной поверхности пластины отсутствует.
В нашем новом случае имеются две частицы, но, поскольку они в каком-то смысле зацеплены друг за друга, они описываются общей волновой функцией, что делает их подобными частице, детектируемой в опыте с двойной щелью. Такие частицы следует рассматривать как единый целостный объект. Согласно теореме Белла, свойства этих частиц не могут быть установлены до их путешествия на край Вселенной, что означает, что любые механизмы, определяющие их свойства, не могут быть локализованы в частице, но должны охватывать всю Вселенную.
Следовательно, если существует некий механизм, решающий, когда именно мой кусок урана должен испускать излучение (как мечтается моей детерминистической душе), такой механизм должен охватывать всю Вселенную. Он не может сводиться к некоей машине, заключенной внутри куска урана, лежащего на моем столе, потому что такая машина должна быть способна управлять состоянием частиц, находящихся на другом конце Вселенной, если они зацеплены с этим куском урана.
Эти результаты часто демонстрируют для опровержения любых попыток утверждать, что такой механизм, определяющий время испускания ураном альфа-частиц, может существовать. Но на самом деле в них следует видеть лишь условия, которым должна удовлетворять такая скрытая машина. Скрытый механизм может существовать – он просто должен быть очень странным. Как сказал Белл, доказавший, что такие скрытые машины должны охватывать всю Вселенную, «доказательство невозможности доказывает только недостаток воображения».
Однако многие не разделяют мое стремление исключить возможность случайности поведения урана. Это может быть связано с тем, что такая случайность образует в научной картине мира зазор, через который в нее может быть введен фактор, милый сердцу многих, – свобода воли.
Некоторые комментаторы утверждали, что если в квантовой физике действует истинная случайность и современное положение вещей не определяется прошлыми событиями, то это свидетельствует о том, что во Вселенной действует свобода воли. Кажется, что квантовые частицы вольны выбирать, куда им лететь и в каком виде проявляться при измерении. Человек, принадлежащий к макромиру, возможно, и не обладает свободой воли, но такие микрочастицы, по-видимому, могут делать что хотят… в разумных пределах.
Свобода воли таких частиц может быть выражением некоей большей свободы воли. Некоторые религиозные мыслители полагают, что известное неизвестное квантовой физики говорит о возможности существования внешнего агента, действующего в нашем мире и влияющего на его развитие. На сегодняшний день мы не располагаем механизмом предсказания исхода измерения системы, находящейся в состоянии квантовой суперпозиции. Если на долговременном масштабе такие исходы соответствуют результатам, которых мы можем ожидать в наблюдаемых случайных процессах, определение отдельных исходов, по-видимому, может быть делом рук такого агента. Такую возможность создает наша нынешняя неспособность объяснить, как макроскопический мир измерений взаимодействует с квантовым миром. Так может ли неизвестное квантовой физики быть местом, в котором находится теистический Бог? Чтобы добиться хоть чего-нибудь, пытаясь понять, может ли Бог скрываться в уравнениях квантовой физики, мне нужно было найти человека, который чувствует себя одинаково уютно и в храме, и в лаборатории. Поэтому я отправился в Кембридж.
Мясник-вегетарианец
Джон Полкинхорн изучал физику под руководством Поля Дирака в Кембридже, а затем – у Ричарда Фейнмана и Мюррея Гелл-Манна в Калтехе. Лучших учителей просто не бывает. Его исследования, в частности, способствовали подтверждению существования кварков, считающихся многими последним уровнем, до которого можно дойти, углубляясь в строение нашей игральной кости.
Сейчас Полкинхорн вернулся в свою альма-матер, и мы договорились встретиться у него дома в Кембридже. Я и сам пять лет занимался исследованиями в Кембридже и всегда с удовольствием туда возвращаюсь, хотя сердце мое отдано темно-синему Оксфорду. Полкинхорн, решивший пройти рукоположение в священники после четверти века работы на передовом крае квантовой физики, – идеальный собеседник для обсуждения теологии квантового непознаваемого. Такой поворот его карьеры многим кажется чересчур резким. Сам он объясняет: «Я оставил науку не потому, что разочаровался в ней, но мне казалось, что примерно за 25 лет я сделал в ней все, что мог. Моя работа была с сильным математическим уклоном, а в математике самые лучшие результаты обычно получают до 45 лет».
Брр… Терпеть не могу, когда так говорят. Я все еще пытаюсь надеяться, что «математика – для тех, кому еще не за сорок» – это миф, что математика – не какой-то там молодежный клуб. Конечно, поскольку я нахожусь по ту сторону этой границы, ничего неожиданного в этом нет. Но пока у меня остаются неразрешенные вопросы, эта надежда заставляет меня продолжать работу. А неразрешенных вопросов на моем столе еще много. Но я, несомненно, могу понять стремление заняться решением новых задач… подобных, например, моим нынешним попыткам разобраться в квантовой физике. Для Полкинхорна таким поворотом стало рукоположение в сан, и он часто шутит над кажущимся противоречием между двумя профессиями, которым он посвятил свою жизнь: «Многие считают, что быть одновременно физиком и священником – занятие странное и даже лицемерное. Это вызывает такое же насмешливое удивление, как, например, мясник, объявивший себя вегетарианцем».
Но сам он думает, что эти две роли гармонично сочетаются друг с другом: «Главная причина попросту в том, что и наука, и теология занимаются поисками истины».
Я поинтересовался, есть ли какие-то вопросы, которые, по его мнению, недоступны той или другой дисциплине.
«Существуют два типа вопросов, на которые наука не может ответить. Некоторые из них происходят из самой науки. Первый тип вопросов – это то, что мы узнали из квантовой физики, что, хотя мир упорядочен, он также обладает смутным и капризным характером, и мы не можем добраться до того ясного, лишенного сомнений постньютоновского мира, который, по-видимому, где-то существует.
Но есть и другие вопросы, которые по самой своей природе не попадают в область действия науки. Я считаю, что наука добилась замечательных успехов, и очень ее уважаю, но этих своих успехов она добилась благодаря ограничению своих притязаний. Наука, по сути дела, задает один-единственный вопрос о том, что происходит в мире: как именно работает мир? При этом она намеренно, по самой своей природе, оставляет за скобками вопросы смысла, ценности и цели».
Мне уже приходилось встречаться с этой предполагаемой разделительной линией: наука определяет «как», а религия – «почему». Мне, однако, кажется, что эта изящная формулировка отражает фундаментально порочный взгляд на науку.
Наука разбирается со множеством вопросов «почему». Почему из моей банки урана вылетают альфа-частицы? Почему траектории планет, обращающихся вокруг Солнца, лежат в одной и той же двумерной плоскости, а не под произвольными углами друг к другу? Почему пчелы строят шестиугольные соты? Почему раз в четыре года численность популяции леммингов резко падает? Почему небо синее? Почему ничто не может перемещаться быстрее скорости света?
Полкинхорн пытается объяснить мне, какие различия он видит между этими двумя подходами.
«Я очень люблю такой бытовой пример: вы заходите ко мне на кухню и видите кипящий чайник. Как ученый я могу объяснить, что чайник кипит, потому что горящий газ нагревает воду и так далее. Но я могу выйти из роли ученого и сказать, что чайник кипит, потому что мне захотелось чаю, – кстати, не хотите ли чашечку?»
Я поймал его на слове и попросил чашку чая. Пока он заваривался, Полкинхорн продолжал: «Мне не нужно выбирать между этими двумя ответами, и если я хочу полностью понять феномен кипения чайника, то я должен ответить на оба вопроса: как оно происходит и почему оно происходит».
Я до некоторой степени согласен с Полкинхорном в том, что наука ограничила свои устремления и занялась более простыми вопросами. Скажем честно, что доказать Великую теорему Ферма легче, чем понять поведение моей кошки или предсказать, что в следующий момент предпримет Полкинхорн. Но это не означает, что наука не может надеяться в конце концов понять все сложности поведения кошки или причуд человеческих желаний.
На мой взгляд, спор о науке и религии пал жертвой нашей ужасной тяги к категоризации всего на свете, зашоренного мышления, которое говорит: «Это вот наука, а это теология, а это искусство, а это психология…» Радует в этом то, что мы разработали множество разных языков, на которых можем говорить об окружающем нас мире. Возможно, все процессы во Вселенной, включая решение Полкинхорна вскипятить чайник, и можно свести к решению волнового уравнения Шредингера. Но, хотя этот язык прекрасно подходит для описания поведения урана в моей банке, он не годится для объяснения миграции стаи птиц, для выражения восторга от музыки Моцарта или для обсуждения безнравственности пыток.
Полкинхорн также признает опасность слишком редукционистских воззрений на реальность: «Иногда, когда я спорю со своими друзьями, придерживающимися твердых редукционистских взглядов и утверждающими, что физика охватывает все на свете, я спрашиваю сначала: “А как насчет математики?” А потом: “А как же музыка?” Разумеется, музыка сводится к вибрациям в ухе, но это и все, что наука может сказать о музыке, – но конечно же далеко не все, что вообще можно сказать о ней. На мой взгляд, очень важно не хвататься то и дело за редукционистский топор, пытаясь порубить все на мелкие кусочки».
Я вернул Полкинхорна к его первому примеру вопроса, на который не может ответить наука. В самом ли деле он верит, что квантовая физика не позволяет мне узнать, когда моя банка урана испустит следующую частицу? Неужели это действительно чистая случайность?
«Вся эта лотерея очень неприятна. Как в казино, по сути дела. Большинство специалистов по квантовой физике просто привыкли к такому положению вещей и заняты своими подсчетами, но мне оно не кажется удовлетворительным. Вопрос в том, какое оно – эпистемологическое или онтологическое.
Эпистемологическая задача имеет ответ – просто мы его не знаем. В онтологической ситуации мы и не можем его знать. И именно такова традиционная интерпретация квантовой теории: мы не можем знать.
Мы знаем, что казино по существу эпистемологично. На происходящее влияют микроскопические эффекты. Мне кажется, что, если проблемы квантовой теории эпистемологичны, нужно составить себе какое-то представление о том, как возникает такое эпистемологическое отчаяние, что мешает нам решить эту задачу. С онтологической точки зрения, по-моему, имеет смысл продолжать упорствовать, пока это вообще возможно. Мы еще не дошли до предела».
Принятый большинством подход к проблемам квантовой физики сводится к тому, что до наблюдения частица представляет собой суперпозицию состояний, описываемую волновой функцией, а наблюдение макроскопическими средствами вызывает скачкообразное изменение ее поведения. Теперь частица имеет всего одно состояние, а волновая функция содержит информацию о вероятности обнаружения частицы в том или ином конкретном состоянии. Объяснить такой скачок никто не пытается. Это воззрение называется копенгагенской интерпретацией, по имени места жительства его главного сторонника, датского физика Нильса Бора. В сущности, это школа квантовой физики под лозунгом «Заткнись и считай».
«Хотя я согласен с копенгагенской интерпретацией квантовой теории, я не считаю ее интеллектуально удовлетворительной. В конечном счете все сводится к тому, что кто-то говорит: “…и потом это происходит”.
Это вызвано вмешательством макроскопических средств. И все – конец разговора. Но это просто победа по определению. В этом и заключается проблема. Загадки остаются неразгаданными».
Учитывая веру Полкинхорна в то, что Бог существует и действует в нашем мире, я спросил, не думает ли он, что неизвестное такой редуцирующейся волновой функции – это то место, в котором может действовать Бог.
«Я не думаю, чтобы Бог решал, распадаться ли ядру вашего урана. Там есть какой-то механизм… нет, “механизм” – не вполне то слово… какое-то влияние, которое устанавливает порядок. Один из парадоксов квантовой теории состоит в том, что и сейчас, 80 лет спустя, мы все еще ее не понимаем».
Исследуя теорию хаоса на первом «рубеже», я прочитал, что Полкинхорн верит, что Бог может влиять на неизвестные нам знаки после запятой. Я поинтересовался, почему он считает тем неизвестным, через которое может действовать Бог, именно теорию хаоса, а не свою собственную область квантовой физики.
«Лет десять назад было такое время, когда научные и богословские сообщества бились над этими формами влияния на мир. Они, разумеется, не разрешили эту проблему – это был бы слишком амбициозный проект. Многие, особенно на Западном побережье Америки, ставили на то, что квантовая теория объяснит все. Мне такая идея казалась чересчур поверхностной. В противовес этому я, может быть, зашел слишком далеко в противоположном направлении. Я не думаю, что все решение сводится только к теории хаоса. Это лишь предположение о том, что физическая Вселенная упорядочена, но порядок ее менее жесткий, чем считал Ньютон».
Но он ни в коем случае не сбрасывает со счетов следствия квантовой физики.
«Открытие фундаментальной непредсказуемости в квантовой теории показывает нам, что мир точно не механистичен, а следовательно, и мы не являемся автоматами в некотором тривиальном и невероятном смысле этого слова».
Интересно, что агент, пытающийся диктовать ход будущего при помощи неизвестного квантовой физики, может действовать, только когда производятся измерения. До тех пор пока измерение не вызовет фазовый переход, уравнения квантовой физики полностью детерминистичны и развиваются линейным, нехаотическим образом, не оставляя никакого места для вмешательства такого агента. В этом заключается одна из причин, по которым религиозно настроенных физиков вроде Полкинхорна, пытающихся найти тот просвет, через который может действовать такой агент, не особенно привлекает неизвестное, следующее из квантовой физики.
Когда я возвращался из Кембриджа, вопрос о соотношении эпистемологии и онтологии казался мне центральным для понимания того, что квантовая физика сообщает нам о непознаваемом. Подобна ли эта ситуация тому, что происходит с игральной костью? Хотя мы не можем точно определить начальные условия броска кости, мы не сомневаемся в их существовании. Квантовая же физика ставит под вопрос саму возможность говорить о точно определенном начальном состоянии моей банки с ураном.
Господствующая сегодня в физике интерпретация утверждает, что нельзя считать, будто бы частицы внутри урана могут одновременно иметь положение и импульс. Такая интерпретация превращает эпистемологию в онтологию. То есть наша неспособность узнать их выражает истинную природу вещей. Как сказал Гейзенберг, «сами атомы или элементарные частицы не реальны; они образуют мир потенциалов и возможностей, а не вещей и фактов».
Что-то из ничего
Хотя кажется, что принцип неопределенности Гейзенберга создает неизвестное или пробел, через которые в мир может вернуться Бог, возможно, что на самом деле он заполняет другой пробел, служащий для большинства источником веры в Бога. Одно из крупнейших неизвестных сводится к вопросу: почему в мире что-то существует? Моя банка урана попала ко мне из компании Images Scientific Instruments на Статен-Айленде через интернет-магазин Amazon. Но если пойти еще дальше, пытаясь определить изначальное происхождение этого урана, мы в конце концов упремся в неизвестность. Потребность в каком-то объяснении этой неизвестности лежит в основе концепций Бога многих культур. Бог является ответом на этот вопрос. Но что это за ответ? Возможно, он просто подчеркивает веру многих в то, что мы не можем знать истинного ответа.
Мне кажется, что большинство ученых, говорящих о Боге, имеют в виду нечто, что давало бы ответ на этот, по-видимому, неразрешимый вопрос: откуда берется все? Они охотно применяют свой научный разум к исследованию того, как устроена уже существующая и работающая Вселенная. Они не ищут в мире следов божественного вмешательства. Такое мировоззрение часто называют деизмом в отличие от теизма. Такого Бога, в сущности, можно приравнять к «тому, чего мы знать не можем».
Разумеется, если попытаться описать, как может выглядеть такой ответ, сталкиваешься с проблемой бесконечной регрессии. Если предположить, что нечто ответственно за создание Вселенной, то, спрашивается, кто создал это нечто? Разумеется, такое «кто» – тоже часть проблемы, потому что мы испытываем непреодолимое стремление персонифицировать эту концепцию.
Именно поэтому многие говорят о трансцендентных определениях, о том, чего нельзя выразить, – чтобы избежать проблемы бесконечной регрессии. Они уклоняются даже от попыток выразить, каким может быть такой ответ. Просто нечто неизвестное и превосходящее наши попытки его познания. Именно таков Бог, определение которого пытался сформулировать ведущий североирландской воскресной утренней радиопередачи, с которым я вступил в спор.
В данном случае Бога определяют как нечто, что не может быть выражено. Но какую силу может иметь такая концепция? Если он не может вмешиваться, не может влиять, не может быть выражен и описан, – то зачем он нам нужен? Именно поэтому все мифотворцы вынуждены отливать своих богов в формы, которые можно выразить, узнать и зачастую персонифицировать. Слишком трансцендентный Бог теряет свое могущество и постепенно исчезает. Именно это случилось с верховными богами или небесными богами многих религий. Религиовед Карен Армстронг пишет в своей книге «Биография Бога» (The Case for God): «Он превратился в Deus otiosus, в “бесполезное”, или “излишнее”, божество, и постепенно исчез из сознания своего народа».
Как заявляет теолог Герберт Маккейб: «Утверждать существование Бога значит утверждать, что существуют не получившие ответа вопросы об устройстве Вселенной». Но он же предостерегает, что порок религий всегда состоит в представлении Бога не как философской идеи, а как конкретного объекта. По его мнению, проблема заключается в том, что религия слишком часто впадает в идолопоклонничество, пытаясь установить слишком личные отношения с такой концепцией Бога.
Трудность состоит в том, что неопределенная, непознаваемая, трансцендентная концепция слишком абстрактна, чтобы многие могли установить с ней какие-то отношения. Она не может предложить того утешения, которого многие ищут в Боге. Поэтому его могущество, возможно, неизбежно должно быть основано на несколько меньшей трансцендентности, несколько большей ощутимости, даже если это и противоречит исходному определению и порождает парадоксальный вопрос о том, «кто создал создателя».
0 = 1–1
Однако вопрос о том, почему существует нечто, а не ничто, может быть не таким уж и непознаваемым. И именно непознаваемое третьего «рубежа» может предоставить способ получения чего-то ex nihilo, из ничего. Как только у нас оказывается кусочек пустого пространства, квантовая физика начинает заполнять его чем-то. Тот вариант принципа неопределенности Гейзенберга, который мы до сих пор рассматривали, касается отношений между положением и импульсом. Но есть и другие физические величины, связанные между собой подобным образом.
Например, принцип неопределенности Гейзенберга связывает энергию и время: если посмотреть, что происходит в, по-видимому, пустой области пространства, то уменьшение временного промежутка исследования такой области приводит к росту неопределенности ее энергетического содержания, что означает, что пустое пространство никогда не может быть действительно пустым. На коротких временных промежутках существует возможность флуктуаций энергии. Поскольку энергия может преобразовываться в массу, это приводит к спонтанному рождению в вакууме частиц. В большинстве случаев они аннигилируют друг с другом и снова обращаются в ничто, но некоторые из них все же выживают. И это дает нам механизм получения чего-то из ничего.
Но откуда берется эта энергия? Не противоречит ли ее внезапное появление закону сохранения энергии, столь милому физике? Кое-кто считает, что суммарное энергетическое содержание Вселенной равно нулю, а потому никакого обмана тут нет. Важно учитывать, что гравитация создает отрицательное энергосодержание. Поэтому Вселенная может возникать из нулевой энергии – из ничего, – поскольку при этом возникает сочетание положительной и отрицательной энергии. Мы попросту наблюдаем действие уравнения 0 = 1–1. 0 есть ничто; 1 плюс –1 – это, соответственно, материя и гравитация, притягивающая эту материю.
Представление гравитации в виде отрицательной энергии может показаться несколько странным, но представим себе крупную массу – например астероид – вблизи Земли. Падая на Землю, астероид увеличивает свою кинетическую энергию, но гравитационное притяжение также возрастает, так как сила гравитационного притяжения увеличивается по мере уменьшения расстояния между двумя массами. Поэтому закон сохранения энергии требует, чтобы гравитационная потенциальная энергия была отрицательной и уравновешивала прирост кинетической энергии.
В соответствии с принципом неопределенности Гейзенберга, из самого факта существования пространства следует, что частицы могут возникать из ничего. Никакой необходимости в создателе нет. Квантовые флуктуации приводят к тому, что мы постоянно видим, как из ничего возникает нечто. Как мы увидим на пятом «рубеже», именно этим Хокинг объяснил испускание частиц черными дырами. Ничто превращается в частицу и античастицу: одна из них оказывается захвачена черной дырой, а вторая улетает прочь. Таким образом, квантовая физика дает частичный ответ на вопрос о получении чего-то из ничего.
Однако нужно по меньшей мере иметь сцену для такой квантовой игры, и здесь на передний план, в свою очередь, выходит вопрос создания пустого пространства. Возможно, именно тут и возникает путаница. Некоторые считают, что пустое пространство и есть ничто. Но это ошибка. Трехмерное пустое пространство, вакуум, есть нечто. Это та арена, на которой могут действовать геометрия, математика, физика. В конце концов, уже тот факт, что мы имеем именно трехмерное, а не четырехмерное пустое пространство, указывает на то, что оно представляет собой нечто. Ничто размерности не имеет.
Сейчас существуют теории, позволяющие объяснить, как пространство и время могут возникать подобно частицам, в качестве флуктуаций квантовой гравитации. Кажется, что их математический аппарат достаточен для того, чтобы создать нечто – чтобы создать Вселенную – из ничего. В конечном счете может оказаться, что уран в моей банке происходит не из магазина Amazon, а из математических выкладок.
Назад: 5
Дальше: Рубеж четвертый: Бумажная Вселенная

