Книга: О том, чего мы не можем знать. Путешествие к рубежам знаний
Назад: Рубеж третий: Банка урана
Дальше: 6
5
Абсолютно необходимое условие прогресса в науке – неопределенность как фундаментальная часть внутренней природы ученого.Ричард Фейнман
Чего только не купишь в интернете! Сегодня почта доставила мне баночку радиоактивного урана-238. Реклама уверяла меня, что она «полезна для опытов по ядерной физике». Меня порадовали комментарии других покупателей: «Очень рад, что мне больше не придется покупать его у ливийцев на парковке торгового центра». Другой покупатель был не столь доволен: «Я приобрел этот продукт 4,47 миллиарда лет назад, а сегодня я открыл банку, и она была наполовину пуста».
Уран встречается в природе, и меня заверили в том, что баночка, стоящая сейчас на моем столе, не представляет никакой опасности. Инструкция только предупреждает меня не размалывать уран и не глотать его. На упаковке написано, что уран испускает излучение с частотой 766 импульсов в минуту. Он испускает несколько видов излучения – альфа-частицы, бета-частицы и гамма-лучи. Но инструкция не может гарантировать, в какой именно момент уран испустит следующую частицу.
Собственно говоря, современная квантовая физика утверждает, что предсказать этот момент вообще невозможно. До сих пор не разработано механизма, который позволил бы точно предсказать, когда радиоактивный уран излучит очередной импульс. Постньютоновская физика, которую мы рассматривали на первом «рубеже», предполагала, что все во Вселенной теоретически должно подчиняться детерминистическому набору математических уравнений и управляться им. Но в начале XX в. группа молодых ученых – Гейзенберг, Шредингер, Бор, Эйнштейн и другие – произвела революцию и утвердила новые воззрения на наши реальные знания о Вселенной. Детерминизм вышел из игры. Теперь, судя по всему, тон задает случайность.
Чтобы понять это неизвестное, необходимо разобраться в одной из самых сложных и противоречащих здравому смыслу теорий за всю историю науки – в квантовой физике. Чтобы оценить трудность этой задачи, достаточно послушать, как те, кто провел в этом мире всю свою жизнь, рассказывают о сложностях, с которыми они сталкивались, осваивая причудливые изгибы его логики. Вернер Гейзенберг вспоминал, как после своих революционных открытий в квантовой физике он «снова и снова повторял вопрос о том, может ли природа действительно быть такой абсурдной, какой она кажется нам в этих атомных экспериментах». Эйнштейн заявил: «Если это правда, то это означает конец науки». Шредингер был настолько потрясен последствиями своей работы, что признавал: «Мне это не нравится, и я сожалею, что приложил к этому руку». Тем не менее эта теория остается одним из самых мощных и испытанных средств, существующих в науке. Ничто не смогло даже поколебать ее статуса одного из величайших научных достижений прошлого века. Так что и нам не остается ничего другого, как нырнуть в этот неопределенный мир. У Фейнмана есть один полезный совет для отправляющихся в такую квантовую экспедицию:
Я собираюсь рассказать вам, как ведет себя Природа. И если вы просто согласитесь, что, возможно, она ведет себя именно таким образом, то вы увидите, что это очаровательная и восхитительная особа. Если сможете, не мучайте себя вопросом «Но как же так может быть?», ибо в противном случае вы зайдете в тупик, из которого еще никто не выбирался. Никто не знает, как же так может быть.
Случайное излучение
Ту революцию, которую совершили эти ученые, превосходно иллюстрируют мои попытки понять, как поведет себя уран в моей банке.
На долгих временных промежутках частота радиоактивного распада приближается к постоянной величине и в среднем вполне предсказуема, в точности как результаты бросков игральной кости. Но физика XX в. утверждает, что между костью и банкой урана есть фундаментальная разница. В случае игральной кости, по крайней мере, создается впечатление, что при наличии достаточного количества данных результат можно предсказать. А вот узнать, когда уран испустит следующую альфа-частицу, по-видимому, невозможно. И полнота информации не играет тут никакой роли. Согласно современной модели квантовой физики, это истинно случайный процесс. В нем можно увидеть пример, опровергающий лапласову концепцию Вселенной с часовым механизмом.
Откровения квантовой физики чрезвычайно неприятны для того, кто ищет определенности и точных знаний. Неужели ничего нельзя сделать, чтобы узнать, когда в банке, стоящей у меня на столе, появится следующая альфа-частица? Возмутительно! Совсем никак не узнать? Вопрос о том, действительно ли этот процесс совершенно случаен и познать его невозможно, или же существует какой-то скрытый, еще не обнаруженный нами механизм, который мог бы объяснить время возникновения излучения, все еще активно обсуждается.
Это неизвестное связано с еще более глубоким уровнем незнания, скрывающим от нас мир предельно малого. Чтобы применить открытые Ньютоном законы движения для вычисления будущего развития Вселенной, необходимо знать положение и импульс всех частиц этой Вселенной. Разумеется, на практике это невозможно, но сделанные в XX в. открытия заставляют думать, что тут существует и более фундаментальная проблема. Даже рассматривая всего один электрон, невозможно одновременно определить его положение и импульс. Наша современная модель предельно малого содержит встроенное ограничение того, что мы можем знать, – так называемый принцип неопределенности Гейзенберга.
Если на первом «рубеже» мы выяснили, что случайность, которую приписывают поведению игральной кости, обозначает всего лишь недостаточное знание, то мир предельно малого, по-видимому, основывается на подлинной случайности: на непознаваемой игральной кости, которая определяет, что случится с куском урана, соседствующим у меня на столе с костью из казино.
Я смирился с непознаваемостью броска игральной кости, поскольку в глубине души я уверен, что эта кость все-таки пляшет в регулярном ритме уравнений Ньютона. Но я не уверен, что когда-нибудь смогу согласиться с непознаваемостью банки радиоактивного урана, который, если верить теории, не танцует ни в чьем ритме. Останется ли его поведение непознаваемым, или же можно ожидать нового теоретического переворота, подобного тому, который открыл нам радикально новые перспективы в начале XX в.?
Волна или частица?
Первые намеки на такую революцию появились, когда ученые пытались понять природу света. Волна это или частица? В своем основополагающем труде по оптике, опубликованном в 1704 г., Ньютон предполагал, что свет имеет корпускулярную природу, то есть состоит из частиц. Если представить свет в виде потока частиц, то его поведение, описанное в книге Ньютона, кажется весьма естественным. Возьмем, например, отражение света. Если нужно узнать, куда будет направлен луч света, падающий на отражающую поверхность, то аналогия с бильярдным шаром, отскакивающим от стенки, позволяет предсказать его траекторию. Ньютон полагал, что такую прямолинейную геометрию световых лучей можно объяснить, только предположив, что свет состоит из частиц.
Однако противники точки зрения Ньютона считали, что природа света гораздо лучше описывается волновой моделью. Казалось, что многие из характеристик света трудно объяснить, если считать его частицей. Эксперимент, поставленный в начале XIX в. английским физиком Томасом Юнгом, по-видимому, забивал гвоздь в гроб представления света как частицы.
Если направить свет на экран, в котором прорезана одна узкая вертикальная щель, и поместить за экраном фотопластинку, способную регистрировать падающий на нее свет, на фотопластинке наблюдается следующая картина: прямо напротив щели и источника света имеется ярко освещенный участок, постепенно тускнеющий по мере удаления от центральной линии.
Пока что результаты опыта соответствуют представлению о корпускулярной природе света: при прохождении частиц сквозь щель могут случаться небольшие отклонения, в результате которых часть света попадает за пределы яркого участка. Правда, если ширина щели мала по сравнению с длиной волны света, то, даже когда такая щель всего одна, по мере удаления от ярко освещенного центрального участка можно наблюдать некоторые волнообразные колебания интенсивности, в которых можно видеть проявление волновой природы света.
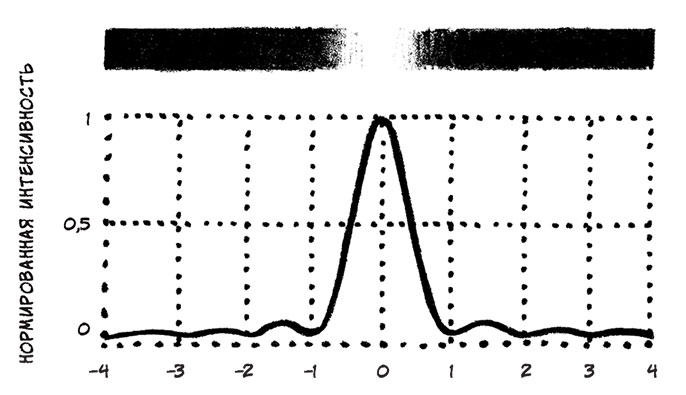
Интенсивность света, зарегистрированного фотопластинкой после прохождения через одну узкую щель
Корпускулярная модель света оказалась в опасности, когда Юнг прорезал в экране вторую вертикальную щель, параллельную первой. Можно было бы ожидать появления двух ярко освещенных участков, расположенных один рядом с другим, каждый из которых соответствовал бы прохождению света через одну из щелей. Но Юнг наблюдал совсем иную картину. На фотопластинке появился ряд чередующихся светлых и темных линий. Как ни странно, некоторые участки пластинки были освещены, только когда была открыта одна щель, и оказывались затемнены после открытия второй. Если свет состоит из частиц, подобных бильярдным шарам, как же может быть, что, когда мы открываем ему новые пути для распространения, он оказывается не в состоянии достичь таких участков? Этот эксперимент породил серьезные сомнения в правоте ньютоновской корпускулярной модели света.
Казалось, что такие светлые и темные полосы может объяснить только волновая модель света. Если в неподвижную воду озера одновременно бросить два камня, то волны, порожденные падением камней, будут взаимодействовать так, что некоторые их части будут объединяться, образуя гораздо более сильные волны, а некоторые другие – гасить друг друга. Если пустить в воду деревянный брусок, такое взаимодействие можно увидеть по соударениям комбинированных волн с его гранью. По всей длине такой грани можно наблюдать последовательность гребней и впадин набегающей волны.
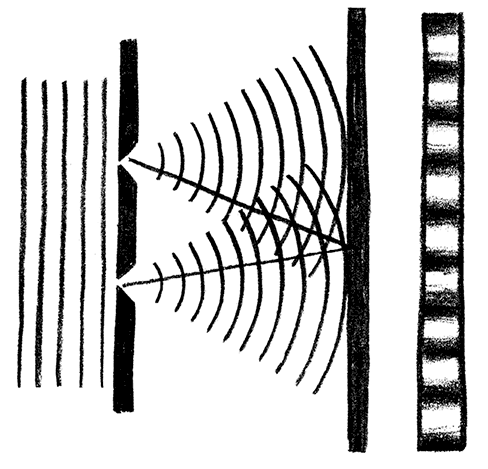
Свет, испускаемый с левой стороны, проходит через экран с двойной щелью и попадает на фотопластинку, установленную справа. Светлые и темные полосы за фотопластинкой иллюстрируют полученную интерференционную картину
Судя по всему, свет, выходящий из двух щелей, образует две волны, взаимодействие между которыми подобно взаимодействию волн, вызванных падением в воду двух камней. На некоторых участках волны света складываются и образуют светлые полосы, а на других – гасят друг друга, создавая темные полосы. Никакая корпускулярная модель света не в состоянии даже приблизительно объяснить возникновение такого рисунка.
Сторонники корпускулярной теории окончательно признали свое поражение в начале 1860-х гг., когда выяснилось, что скорость распространения света точно соответствует предсказанию новой теории электромагнитного излучения Джеймса Клерка Максвелла, основанной на волновой модели. Вычисления Максвелла показали, что свет есть не что иное, как форма электромагнитного излучения, описываемая уравнениями, решения которых представляют собой волны с разными частотами, соответствующие разным видам электромагнитного излучения.
Однако в этой истории случился еще один неожиданный поворот. Если опыт Юнга подтолкнул ученых к признанию волновой модели света, то результаты двух других экспериментов, проведенных в конце XIX в., можно было объяснить, только предположив, что свет распространяется дискретными порциями, или пакетами. Иначе говоря, квантуется.
Изготовление волновой какофонии
Первый намек на то, что свет может и не быть волнообразным, появился из попыток понять световое или электромагнитное излучение, возникающее в угольных печах, ставших двигателем промышленной революции. Тепло есть движение, но если привести в движение электрон, то, поскольку у него есть отрицательный электрический заряд, он будет испускать электромагнитное излучение. Поэтому раскаленные предметы и светятся: движущиеся в них электроны излучают. Электрон можно представить себе в виде человека, держащего в руке один конец скакалки: когда рука человека движется вверх и вниз, скакалка начинает совершать волнообразные колебания. Каждая волна имеет частоту, равную числу пульсаций волны в секунду. Именно частота определяет, например, цвет видимого света. Красный свет имеет низкую частоту, синий – более высокую. Частота также играет роль в определении энергии, содержащейся в волне. Чем выше частота, тем выше энергия волны. Другой фактор, определяющий энергию волны, – это ее амплитуда. Амплитуда определяет размах волны. Возвращаясь к тому же примеру, чем энергичнее мы раскачиваем скакалку, тем с большим размахом она колеблется. На протяжении многих столетий ученые использовали основную частоту излучения в качестве меры температуры. Красное каление. Белое каление. Чем горячее огонь, тем выше частота испускаемого им света.
Мне посчастливилось увидеть одну из таких угольных печей в действии во время посещения насосной станции в городе Паплвик под Ноттингемом. Раз в месяц они устраивают «паровой день» и зажигают свои печи. Печь находится в замечательно украшенном викторианском здании. Утверждается, что стоимость постройки станции была настолько меньше выделенного бюджета, что оставшихся средств хватило на украшение насосной. Она кажется храмом, но посвященным не Богу, а науке промышленной эры.
Температура внутри печи в Паплвике была где-то в районе тысячи градусов Цельсия. Ученых конца XIX в. интересовало, какой частотный спектр имеет свет при фиксированных значениях температуры внутри печи. Закрытая печь может достичь термодинамического равновесия, при котором все излучение, испускаемое в результате вызванных нагревом колебаний атомов, заново поглощается, так что никакой потери электромагнитного излучения не происходит.
Какие частоты излучения можно найти в печи, достигшей такого равновесия? Представим себе множество натянутых виолончельных струн. Суммарная энергия вибрирующей струны зависит от частоты и амплитуды ее вибрации. Для запуска волн с более высокой частотой требуется больше энергии, но эту разницу можно компенсировать, придав волне меньшую амплитуду. В соответствии с классической моделью фиксированное количество энергии теоретически может вызвать волновые колебания любых частот, но их амплитуда будет уменьшаться по мере увеличения частоты.
Теоретический анализ спектра, по-видимому, указывал на возможность возникновения в печи волн любой произвольной частоты. И тем не менее, когда я заглянул внутрь печи в Паплвике, я не получил дозу высокочастотного рентгеновского излучения. Хотя и должен был ее получить в соответствии с предсказаниями волновой теории электромагнетизма. Более того, если сложить все вклады разных частот внутри печи, находящейся в состоянии теплового равновесия, то анализ, основанный на представлении света в виде колебательной волны, приводит к абсурдному выводу о том, что внутри печи заключена бесконечно большая энергия. Будь это так, печь в Паплвике просуществовала бы недолго.
Оказывается, что для каждой температуры существует некоторая пороговая частота, за которой запуска волновых колебаний не происходит. Классическая картина этой ситуации такова. Если свет подобен вибрирующей струне виолончели, то печь должна генерировать волны всех частот, причем число волн должно возрастать с частотой. При низких частотах этот график соответствует действительности, но по мере роста частоты мы видим, что интенсивность радиации на высоких частотах спадает и начиная с некоторой точки (зависящей от температуры) вообще не наблюдается волн с частотой, большей этого числа.
В 1900 г. немецкий физик Макс Планк изучил экспериментально полученное распределение частот в печи, подобной той, что я видел в Паплвике, и предложил интересную идею, объясняющую, как можно получить истинную кривую вместо той бессмыслицы, которую дает классическая интерпретация света как виолончельной струны.
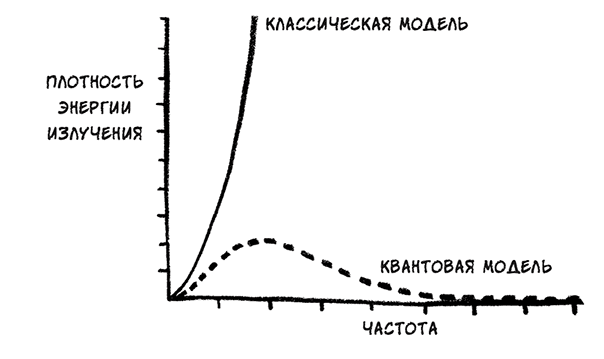
Частоты внутри закрытой печи в соответствии с предсказаниями классической и квантовой моделей
Он предположил, что для каждой частоты электромагнитного излучения существует минимальная энергия, необходимая для возникновения такого излучения. Энергию волны, вибрирующей на некоторой частоте, нельзя непрерывно уменьшать, ожидая при этом, что вибрация будет продолжаться. В некоторой точке такого уменьшения энергии волна перестанет вибрировать все с меньшей и меньшей амплитудой и просто исчезнет, превратится в плоскую линию. Более того, модель Планка предполагала, что плавного изменения вообще не происходит. При каждом увеличении энергии она возрастает дискретным скачком. Такие скачки энергии чрезвычайно малы, и заметить их очень трудно, если специально не искать. Но с учетом этого предположения Планка расчетные значения интенсивности электромагнитного излучения на разных частотах точно совпали с результатами наблюдений излучения, возникающего в печи.
То есть Вселенная может оказаться не такой гладкой и непрерывной, какой считали ее ученые до конца XIX в. атомисты – те, кто верил, что мир состоит из элементарных составляющих, – даже и подумать не могли, что атомистическая философия может быть применима к энергии. В приложении к виолончельной струне это означает, что, когда я провожу по струне смычком, увеличивая громкость звучания, она на самом деле возрастает ступенчато, хотя человеческое ухо слышит постепенное, непрерывное увеличение громкости. Ступеньки эти очень малы. Для каждой частоты ν энергия увеличивается порциями, равными hν, где h – величина, называемая постоянной Планка. В этом числе, определяющем размеры шага возрастания энергии и измеряемом в джоуль-секундах, первые 33 знака после запятой – нули и лишь затем появляется первая ненулевая цифра:
h = 6,626 · 10–34 Дж · с.
На этом этапе у Планка не было реального физического объяснения существования таких ступеней энергии, но с математической точки зрения это решение идеально объясняло экспериментально наблюдаемое поведение электромагнитного излучения в печах, подобных печи в Паплвике. К представлению о свете как частице ученых заставило обратиться объяснение результатов другого эксперимента, данное Эйнштейном. И энергия таких частиц оказалась равна hν.
Электроны на выброс: фотоэлектрический эффект
Металлы так хорошо проводят электричество потому, что в них имеется множество свободных электронов, способных перемещаться внутри металла. Поэтому, направив на кусок металла электромагнитное излучение, можно выбить из него такие электроны. Энергия волны передается электрону, и его собственная энергия возрастает настолько, что он может преодолеть силы, удерживающие его внутри металла. Именно этот процесс был ключевым элементом открытия электрона Томсоном, описанного на предыдущем «рубеже».
Если считать электромагнитное излучение волной, то должна существовать возможность увеличить энергию такой волны до того уровня, на котором она сможет выбить из металла электрон. Чем выше энергия волны, тем более сильный толчок получит электрон и тем большей будет скорость его вылета. Как было описано в предыдущем разделе, есть два способа увеличить энергию волны – или вибрирующей струны виолончели. Один состоит в повышении частоты волны, в ускорении вибрации. Если поступить таким образом, то, действительно, скорость выбиваемых электронов соответственно возрастает. Но если сохранять частоту неизменной, то увеличить энергию можно путем повышения амплитуды волны, то есть громкости звука струны. Странность заключается в том, что увеличение интенсивности волн при постоянной частоте, оказывается, не влияет на скорость, с которой вылетают электроны. Вместо этого возрастает число электронов, выбиваемых из металла.
Более того, уменьшая частоту волны при одновременном увеличении амплитуды, суммарную энергию можно поддерживать на постоянном уровне, и тем не менее в некоторой точке такая волна, по-видимому, утрачивает способность к выбиванию электронов. Существуют такие частоты, ниже которых, как бы громко я ни играл на виолончели, энергия не выбивает ни одного электрона. Напротив, в случае высокочастотной волны громкость можно уменьшать сколько угодно: даже волна чрезвычайно низкой интенсивности по-прежнему способна выбивать электроны. Что происходит? Как объяснить такое странное поведение, известное в науке под названием фотоэлектрического эффекта?
Решение заключается в смене модели. До сих пор мы рассматривали процесс, на входе которого была волна, а на выходе – частица. Что, если попробовать другой вариант: частица на входе и частица на выходе? Возможно, ключевой элемент понимания действия падающего электромагнитного излучения следует искать в его корпускулярной природе.
Именно в этом и состоял коренной сдвиг мировоззрения, совершенный Эйнштейном в 1905 г., который многие называют annus mirabilis. В этом же году он предложил специальную теорию относительности, за которую мы возьмемся на одном из следующих «рубежей», а также теорию броуновского движения, обеспечившую самую убедительную поддержку идеи атомарного устройства материи, как было описано в предыдущей главе.
Эйнштейн предположил, что электромагнитное излучение или свет следует уподобить не волне, а пулеметной очереди, состоящей из мельчайших бильярдных шаров, в точности как предлагал еще Ньютон. Энергия каждой отдельной частицы зависит от частоты излучения. Эта новая идея дает нам модель, идеально описывающую те результаты, которые мы наблюдали в лаборатории. Каждый бильярдный шарик света имеет энергию, соответствующую минимальной энергии, вычисленной Планком для объяснения поведения излучения в печи. Так, электромагнитное излучение с частотой ν в модели Эйнштейна следует рассматривать как набор шариков, каждый из которых имеет энергию, равную hν. Введенные Планком скачки энергии попросту соответствуют добавлению к излучению новых световых шариков. Эйнштейн назвал такие шарики квантами света, но в середине 1920-х гг. они получили новое название, и теперь мы знаем их под именем фотонов.
Фотонный бильярд
Как же такая корпускулярная модель света объясняет поведение электронов, выбиваемых из металла? Снова представим взаимодействие как бильярдную игру. Фотоны сталкиваются с поверхностью металла. Если фотон попадает в электрон, электрону передается энергия, и электрон улетает. Но, чтобы быть выбитым из металла, электрон должен получить определенное количество энергии.
Энергия каждого налетающего фотона зависит только от частоты светового излучения. Если частота излучения слишком мала, то энергии каждого налетающего фотона недостаточно для выбивания электрона. Интенсивность излучения можно увеличивать сколько угодно: от этого возрастает число шариков, налетающих на металл, но энергия каждого отдельного шарика остается той же. Вероятность попадания в электрон увеличивается, но, поскольку каждый шарик так же бессилен, как и все остальные, электрон так и останется невыбитым. В волновой модели электрон постепенно накапливал бы поступающую энергию до тех пор, пока она не станет достаточной для его вылета. В корпускулярной модели электрон можно толкать сколько угодно раз, но ни один из таких толчков не будет достаточно сильным, чтобы выбить его. Точно так же можно слегка тыкать человека пальцем: сколько бы ни было таких слабых прикосновений, человек от них не упадет.
Но если частота налетающего излучения превышает некоторое значение, энергия каждого шарика становится достаточной для выбивания электрона, в который он попадает. Вместо сотен легких прикосновений человек получает один мощный толчок, который его опрокидывает. По сути дела, шарик передает электрону достаточное количество энергии, и результирующей энергии электрона хватает, чтобы преодолеть силы, удерживающие его в металле. Увеличение интенсивности излучения означает выстреливание большего количества шариков, что приводит лишь к росту числа испускаемых электронов. Поэтому мы наблюдаем выбивание большего количества электронов, а не выбивание электронов с большей скоростью.
Согласно модели Эйнштейна, кинетическая энергия испускаемого электрона прямо пропорциональна частоте. Интересно отметить, что эта зависимость не была до этого ни установлена на опыте, ни предсказана теоретически, что придало модели Эйнштейна наилучшее свойство любой качественной научной теории: она могла не только объяснить факты, уже наблюдавшиеся в лаборатории, но и предсказать некие новые явления, которые впоследствии можно было проверить. Это было особенно важно, потому что многие ученые отнеслись к модели Эйнштейна чрезвычайно скептически. Уравнения Максвелла, описывающие электромагнитное излучение в терминах математического представления волн, работали так хорошо, что ученым требовались более весомые аргументы в пользу пересмотра их мировоззрения.
Одним из таких скептиков был американский физик Роберт Эндрюс Милликен. Но предпринятые им попытки опровержения предложенной Эйнштейном модели бильярдных шариков света в конечном счете привели к подтверждению предсказания Эйнштейна о прямой пропорциональности кинетической энергии вылетающих электронов частоте падающего излучения. До этого Милликен занимался исследованиями, в которых ему удалось определить заряд электрона, а впоследствии, доказав, что излучение, регистрируемое детекторами на Земле, имеет внеземное происхождение, ввел в обиход понятие космических лучей. Работы Милликена были удостоены Нобелевской премии по физике в 1923 г., всего через два года после того, как эту премию получил Эйнштейн.
Нобелевская премия 1921 г. была присуждена Эйнштейну именно за объяснение фотоэлектрического эффекта. Теорию относительности Нобелевский комитет не признал достойной премии. Идеи Эйнштейна дали сторонникам корпускулярной теории возможность оправиться от поражения, которое они признали несколькими десятилетиями раньше, после открытий Максвелла. За этим, однако, последовала контрреволюция, когда обнаружилось, что частицы, такие как электроны, имеют характеристики, присущие скорее волнам, чем дискретным частицам. Казалось, что и свет, и электроны ведут себя и как частицы, и как волны. В зарождавшейся новой теории оказывалось, что в этом споре правы были все.
Несмотря на переворот мировоззрения, произведенный Эйнштейном, опыты, которые лучше объяснялись волновой природой света, не были опровергнуты. Как ни странно, казалось, что выбор используемой модели света определялся условиями эксперимента. Наступила эпоха корпускулярно-волнового дуализма.
Вспомним, что наиболее сокрушительным доказательством того, что свет – это волна, а не частица, стал поставленный Юнгом опыт с двойной щелью. В случае фотоэлектрического эффекта убедительный довод в пользу того, что электромагнитное излучение состоит из частиц, был получен благодаря весьма элегантному использованию свойств электрона как частицы. Но работает ли этот диалог в обратную сторону? Что, если пригласить электрон поучаствовать в эксперименте Юнга с двойной щелью? Как выяснилось, электронная бомбардировка экрана с двойной щелью смогла произвести совершенно ошеломляющий эффект в нашем восприятии реальности.
Опыты с электронами
Одно из наиболее интересных следствий из квантовой механики состоит в том, что частица, подобная электрону, по-видимому, может одновременно находиться в нескольких разных местах вплоть до момента ее наблюдения – а тогда место реального нахождения частицы определяется, насколько можно судить, случайным образом. Сейчас ученые полагают, что речь здесь идет об истинной случайности, а не просто о недостатке информации. Если повторить этот эксперимент несколько раз в тех же условиях, результаты каждый раз могут быть разными. Именно эта неопределенность положения в конечном счете виновата в том, что частицы моего куска урана внезапно оказываются вне, а не внутри банки, стоящей на моем столе.
Наиболее яркую иллюстрацию этого явления можно получить, повторив опыт Юнга с двойной щелью, но не со светом, а с электронами. Один из моих коллег по Оксфорду, физик, пригласил меня в свою лабораторию, чтобы я мог увидеть ту странную игру, в которую, как кажется, играют электроны, своими глазами. Я читал о ней много раз, но, как сказал Кант, «всякое наше знание начинается с чувств».
Я счел своим долгом предупредить коллегу о своих сложных отношениях с экспериментами. В школе никто не соглашался ставить опыты в паре со мной, потому что у меня они никогда не получались. Это и было одной из причин, по которым меня привлекла теоретическая часть науки – в ней беспорядок физического мира можно хоть как-то контролировать. Но коллега заверил меня, что этот опыт работает вполне надежно.
Для начала мы установили источник, испускающий электроны со скоростью, при которой они регистрируются пластиной детектора по одному. Затем я поставил между источником и детектором экран с двумя щелями. Сначала я посмотрел, что происходит, когда одна из щелей закрыта. Электроны, прошедшие сквозь щель, попадали в пластину детектора, и после достаточного числа таких попаданий можно было увидеть возникновение некоей структуры.
На участок, расположенный на прямой линии, проведенной через источник и щель, электроны попадали с высокой интенсивностью. При смещении в обе стороны от этой центральной линии все еще можно было видеть попадания электронов, но число их уменьшалось по мере удаления от нее. В некоторых случаях электроны, пролетающие сквозь щель, отклонялись и их траектории изгибались в обе стороны от центральной линии. Пока ничего странного. Но потом я открыл вторую щель.
Если бы электроны вели себя как классические частицы, можно было бы ожидать увидеть напротив двух щелей два участка высокой интенсивности, в которые электроны попадали бы, пройдя через одну или другую щель. Но я их не увидел. Вместо этого начала возникать интерференционная картина, подобная той, которую видел Юнг в своем опыте со светом. Она лучше описывалась аналогией с волной, проходящей сквозь такие щели и создающей две новые волны, интерферирующие друг с другом.
Вспомним, однако, что опыт был поставлен так, чтобы в каждый момент через экран пролетал всего один электрон. То есть это не было волноподобным взаимодействием множества электронов. Один-единственный электрон вел себя как волна. Еще более непонятным был тот факт, что на пластине детектора обнаружились участки, до которых не долетал ни один электрон, хотя при одной открытой щели электроны могли попадать в эти точки. Что же происходило? Я открыл еще одну щель, создав тем самым несколько возможных путей к такой точке детектора, но и такие новые возможности не привели к попаданию в нее электронов.
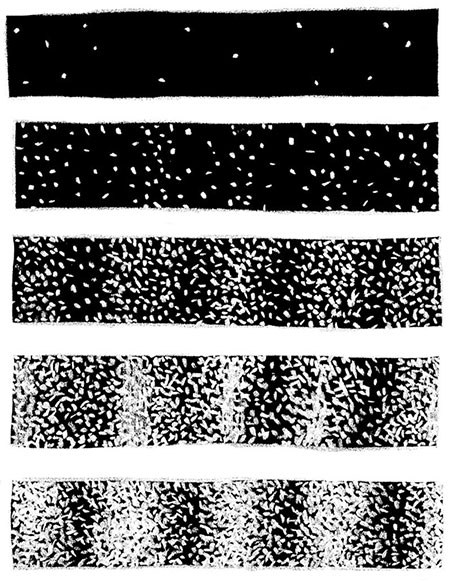
По увеличении числа зарегистрированных электронов возникает интерференционная картина
Кант утверждал, что всякое знание начинается с чувств, но «переходит затем к рассудку и заканчивается в разуме, выше которого нет в нас ничего для обработки материала созерцаний». Как же ученым удалось выделить разумное зерно из странного поведения таких одиночных электронов, пролетающих сквозь экран?
Электрон-шизофреник
Как может электрон, проходящий сквозь одну из щелей, знать, открыта или закрыта вторая щель? Вторая щель находится на некотором расстоянии от той, через которую пролетает электрон. Не может же электрон разделиться надвое и пролететь через обе щели. Как это ни удивительно, нужно отбросить идею о том, что до обнаружения электрона он может находиться в какой-либо определенной точке пространства. Вместо этого электрон следует математически описывать волновой функцией, которая дает целый диапазон возможных положений. Такова была новая, революционная точка зрения, которую предложил в 1926 г. австрийский физик Эрвин Шредингер. Амплитуда такой волны содержит информацию о вероятности нахождения электрона в определенной области пространства на момент его наблюдения.
Можно спросить: волна чего? Что тут, собственно, колеблется? На самом деле речь идет не о физическом объекте, а скорее о волне амплитуды вероятности. Точно так же «волна преступности» – это не волна из преступников, а информация о вероятности совершения преступлений в определенном районе. Волна – это просто математическая функция, а математическая функция подобна машине или компьютеру: в нее вводят информацию, а она вычисляет и выдает ответ. В волновую функцию электрона вводят область пространства, а на выходе получают вероятность обнаружения электрона именно в этой области. Как ни странно, такую частицу следует считать вовсе не физическим объектом, а изменяющейся математической конструкцией. Ее называют волновой функцией, потому что многие черты функций, описывающих такие вероятности, совпадают с характеристиками классических волновых функций. Гребни и впадины содержат информацию о возможном местоположении электрона. Чем больше амплитуда волны, тем выше вероятность обнаружить электрон в данной области пространства.
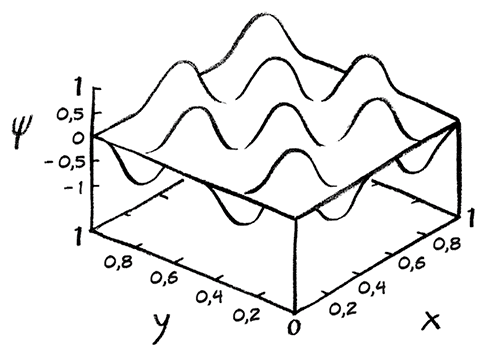
Квантовая волна: чем выше волна, тем больше вероятность обнаружить электрон в данной точке пространства
Итак, поведение электрона описывает волна, и, когда такая волна сталкивается с экраном, в котором прорезаны две щели, взаимодействие с экраном изменяет ее. В результате получается новая волна, свойства которой и создают ту странную интерференционную картину, которую я наблюдаю на пластине детектора. Именно в момент обнаружения электрон решает наконец, в какой точке пластины он будет находиться. Волновая функция дает вероятность нахождения электрона в том или ином месте, но в момент обнаружения жребий оказывается брошен и вероятность сменяется определенностью. Волны больше не существует, и электрон снова выглядит частицей, попадающей в одну-единственную точку пластины детектора. Однако при каждом повторении этого опыта электрон может появляться в каких-нибудь других местах. Чем больше мы направляем на экран электронов, тем большая статистика, закодированная в волнах, становится видна по мере проявления картины распределения обнаруженных электронов. Но физика утверждает, что предсказать, в какой именно точке пластины в каждом отдельном случае будет обнаружен очередной электрон, невозможно.
Интересно было бы вернуться к исходному опыту Юнга со светом, но интерпретировать его в свете (прошу прощения за каламбур) сделанного Эйнштейном открытия частиц, составляющих свет, – фотонов. Уменьшая интенсивность источника света в опыте Юнга, можно дойти до такой низкой энергии излучения, которая будет соответствовать испусканию в экран с двойной щелью одиночных фотонов.
Как и электрон, фотон, попадающий на фотопластинку, оставляет на ней единственный точечный след, соответствующий его корпускулярной природе. А что происходит с интерференционной картиной Юнга? Нечто удивительное. Если продолжать обстреливать экран с двойной щелью одиночными фотонами, то через некоторое время накапливающиеся на фотопластинке светлые точки постепенно начинают образовывать все ту же интерференционную картину. То, что наблюдал Юнг, не было результатом падения на пластинку непрерывной волны – это была иллюзия. На самом деле картина состояла из миллиардов и миллиардов пикселей, каждый из которых соответствовал обнаружению одного фотона. Чтобы дать представление о числе фотонов, попадавших на пластинку, можно сказать, что стоваттная лампочка испускает около 1020 (то есть ста миллиардов миллиардов) фотонов в секунду.
Волновые характеристики света аналогичны свойствам электрона. Волна есть математический объект, определяющий вероятное местоположение фотона на момент его обнаружения. Волновая природа света означает, что он представляет собой не колеблющуюся волну, подобную волнам на воде, а волнообразную функцию, содержащую информацию о том, где можно будет найти фотон после его обнаружения. До того как он попадет на пластину детектора, он, как и электрон, по-видимому, проходит одновременно через обе щели и принимает решение о своем положении в пространстве только в момент наблюдения.
Именно эта концепция наблюдения делает квантовую физику такой странной. Пока я не потребую от детектора определить, где находится электрон, эту частицу следует считать вероятностно распределенной по пространству, причем распределение такой вероятности описывается математической функцией, обладающей волновыми свойствами. Воздействие двойной щели на эту математическую функцию изменяет ее таким образом, что электрон не может попасть в некоторые точки пластины детектора. Но, как только частица будет обнаружена, жребий будет брошен – и волне вероятности придется выбрать положение данной частицы.
Я помню то Рождество, когда я впервые прочитал об этой сумасшедшей истории, в которой что-то может оказаться сразу в нескольких местах. Помимо игрушек и сластей Дед Мороз оставил для меня под елкой книжку с забавным названием «Мистер Томпкинс в мягкой обложке», написанную физиком Георгием Гамовым. В ней рассказывается история попыток мистера Томпкинса выучить физику на вечерних лекциях, которые читает известный профессор. Беда в том, что посреди лекции мистер Томпкинс неизменно засыпает.
В его снах микроскопический квантовый мир электронов увеличивается до макроскопических размеров, и мистер Томпкинс оказывается в квантовых джунглях, полных тигров и обезьян, которые одновременно находятся в нескольких разных местах. Когда на мистера Томпкинса нападает большая стая несколько размытых тигров, профессор, сопровождающий его в снах, выпускает по ним множество пуль. Одна из пуль попадает в цель, и стая тигров внезапно превращается в одного-единственного «наблюдаемого» тигра.
Помню, как меня очаровал этот фантастический мир и еще больше взволновало то обстоятельство, что он не был таким уж фантастическим. К тому времени я начал было сомневаться в существовании Деда Мороза, учитывая, что за одну ночь он должен посетить миллиард детей по всему миру, но эта книга восстановила мою веру. Конечно же Дед Мороз использует квантовую физику! Если его никто не наблюдает, он может одновременно находиться во множестве разных каминных труб.
Квантовая антропология
Чтобы подчеркнуть ту странную роль, которую играет наблюдение, можно вернуться к опыту с двойной щелью и поставить на одной из щелей детектор, чтобы попытаться подглядеть, в какую именно щель «на самом деле» проходит электрон. В этом случае интерференционная картина исчезает. Акт определения щели, через которую пролетает электрон, изменяет природу описывающей его волновой функции. Теперь на пластине детектора видны два светлых участка, расположенных напротив щелей, – никакой интерференции. Моя попытка познания изменяет поведение электрона.
В качестве возможной, хотя и не вполне честной аналогии можно представить себе антрополога, наблюдающего ранее неизвестное племя индейцев Амазонки. Его наблюдение неизбежно изменяет поведение индейцев. Наблюдать без взаимодействия с племенем и без какого-либо влияния на его поведение невозможно. В случае электрона это еще более очевидно. Чтобы узнать, через какую щель он пролетает, на него нужно «посмотреть», но для этого с ним необходимо провзаимодействовать. Например, в таком взаимодействии может быть использован световой фотон, отражающийся от электрона и возвращающийся в детектор. Но такой фотон обязательно производит некоторое изменение энергии, импульса или положения электрона. Он не может взаимодействовать без какого-либо изменения. Собственно говоря, такое взаимодействие может быть не таким явным, как отражение фотона от электрона. Оно может быть и более тонким. Если детектор, установленный на одной из щелей, не обнаруживает электрона, из этого можно заключить, что он прошел через вторую щель. Но никакого отражения фотона от электрона в этом случае не происходит. Такое измерение положения электрона происходит без взаимодействия.
Есть один очень странный мысленный эксперимент, использующий такой акт наблюдения за тем, как электроны проходят через щель в экране. Предположим, мы сделаем бомбу, которая может быть приведена в действие при попадании в ее датчик единственного электрона. Проблема в том, что нельзя гарантировать, что бомба сработает. С классической точки зрения единственный способ ее испытания сводится к довольно бессмысленному действию – запуску в бомбу электрона. Если бомба взорвется, значит, она была настоящая. Если нет – муляж. Но в любом случае после такого испытания мы остаемся без бомбы.
Как ни странно, для обнаружения действующих бомб, не требующего их взрыва, можно использовать опыт с двойной щелью. Вспомним, что на пластине есть участки, в которые электрон, если он действительно одновременно проходит через обе щели, попасть не может. Если в такой точке все-таки обнаруживается электрон (традиционным, невзрывным способом), значит, мы подглядывали и заставили этот электрон выбрать одну из щелей. Этот участок мы и будем использовать в качестве «бомбового детектора». Поставим датчик бомбы на одну из щелей: если эта бомба – муляж, то датчик ее не взорвет. То есть в случае муляжа мы не производим наблюдения. Значит, электрон проходит через обе щели и не может попасть в «бомбовый детектор».
А что, если это не муляж? В таком случае, если электрон пролетит через эту щель, датчик его зарегистрирует и взорвет бомбу. Так себе результат. Но, поскольку теперь мы определяем, через какую щель пролетает электрон, он пролетает только через одну щель и имеет шанс попасть в наш «бомбовый детектор». Поэтому обнаружение электрона в «бомбовом детекторе» должно означать, что бомба заряжена. Заряженная бомба является механизмом детектирования электронов. В половине случаев детектирования электронов они пролетают через щель, на которой установлен датчик, и бомба взрывается. Но в остальной половине случаев бомба определяет, что электроны пролетели через другую щель, интерференционная картина не может возникнуть, электроны могут попасть в «бомбовый детектор», и тем не менее бомба не взрывается. Электрон дал нам информацию о том, через какую щель он пролетел, но такой акт «наблюдения» не требовал ни слежения за электроном, ни его столкновения с фотоном, ни взрыва бомбы.
Такие странные последствия акта наблюдения также можно использовать для прекращения распада в банке урана с моего стола. Если постоянно производить множество мини-наблюдений, пытаясь застать уран за испусканием излучения, то такие наблюдения могут «заморозить» уран и остановить его распад. Старая поговорка утверждает, что кастрюля, за которой следят, никогда не закипит, – только в квантовом варианте место кастрюли занимает банка, полная урана.
Тот факт, что постоянное наблюдение за нестабильной частицей может каким-то образом заморозить ее и остановить ее трансформации, первым осознал специалист по расшифровке кодов, математик Алан Тьюринг. С тех пор это явление стало известно под названием квантового эффекта Зенона, по имени греческого философа, который полагал, что поскольку моментальные снимки летящей стрелы не показывают никакого движения, то стрела вообще не может двигаться.
Представим себе частицу, которая может иметь два состояния, ЗДЕСЬ и ТАМ. Пока ее никто не наблюдает, она находится в смешанном состоянии, но акт наблюдения заставляет ее выбрать одно из них. Если она выбрала состояние ЗДЕСЬ, то после наблюдения она начинает постепенно возвращаться в смешанное состояние, но если быстро произвести новое наблюдение, пока она в основном еще находится ЗДЕСЬ, то, по всей вероятности, она снова перейдет в состояние ЗДЕСЬ. Таким образом, если постоянно наблюдать такую частицу, она никогда не приобретет достаточной доли состояния ТАМ, чтобы ее можно было наблюдать ТАМ. Это похоже на ситуацию с двумя стаканами, до половины налитыми водой, если при каждом наблюдении мы должны переливать воду из одного стакана в другой, наполняя его до краев. После наблюдения можно начать снова переливать воду в пустой стакан, но, если произвести новое наблюдение достаточно быстро, во втором стакане еще почти не будет воды, так что проще всего будет снова наполнить тот стакан, который уже почти полон. Если каждый раз производить наблюдение достаточно быстро, можно сделать так, чтобы полный стакан постоянно оставался полным.
Мои дети увлекаются научно-фантастическим телесериалом «Doctor Who», как увлекался им в детстве и я. Из всех видов инопланетян в нем самыми страшными нам кажутся «плачущие ангелы» – каменные статуи, похожие на тех, что стоят на нашем местном кладбище. Они остаются неподвижными, пока на них смотришь, не отводя глаз. Но стоит только моргнуть, и они могут двигаться. Теория утверждает, что стоящая на моем столе баночка урана похожа на плачущего ангела. Если я буду постоянно наблюдать уран – что, очевидно, требует несколько большего, чем простое созерцание банки, – я могу заморозить его так, что он перестанет испускать излучение.
Хотя Тьюринг впервые выдвинул эту идею в качестве теоретического последствия математических выкладок, оказалось, что она была не просто математической выдумкой. В последнее десятилетие были поставлены некоторые эксперименты, продемонстрировавшие реальную возможность использования наблюдений для торможения развития квантовых систем.
Множественные истории
Из квантовой физики, по-видимому, следует, что в опыте с двойной щелью электрон имеет бесконечное количество вариантов будущего до тех пор, пока мы не произведем его наблюдения. В этот момент бросок некоей неведомой квантовой кости определяет, какое именно из этих будущих должно осуществиться. Я, предположим, могу смириться с тем, что будущее невозможно узнать, пока оно не станет настоящим. В конце концов, если я беру свою игральную кость, собираясь бросить ее три раза, у нее существуют 6 · 6 · 6 = 216 разных вариантов будущего, каждый из которых может осуществиться. Как акт бросания кости выбирает одно из этих 216 возможных будущих, так и акт наблюдения электрона определяет одно из его многочисленных возможных положений. Однако из другого неожиданного поворота опыта с двойной щелью следует, что прошлое тоже не определено единственным образом.
Более того, получается, что действия, осуществляемые в настоящем, способны изменить прошлое. Узнать, через какую именно щель пролетел электрон, можно спустя долгое время после прохождения им экрана. В момент, непосредственно предшествующий попаданию электрона в пластину детектора, прямо перед электроном можно поставить наблюдательное устройство. Назовем такое устройство «щелевым наблюдателем».
Предположим, что наш опыт с двойной щелью поставлен в космическом масштабе. Поставим на одном краю Вселенной источник электронов и расположим прямо перед ним экран с двойной щелью. Поместим пластину детектора на другом краю Вселенной. В такой конфигурации электрону потребуется много лет, чтобы пересечь все это пространство и наконец попасть в пластину. Поэтому когда электрон пролетает через экран с двойной щелью, он не знает, будем ли мы наблюдать его при помощи нашего «щелевого наблюдателя».
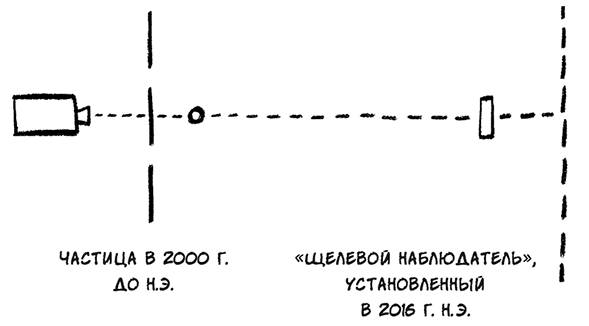
Решение об установке на пути частицы «щелевого наблюдателя», принятое в 2016 г. н. э., может изменить поведение частицы в 2000 г. до н. э.
Если мы все-таки используем «щелевой наблюдатель» много лет спустя, это будет означать, что за много лет до того электрон должен был пролететь через ту или другую щель. Но если мы не используем «щелевой наблюдатель», то много лет назад электрон должен был пролететь через обе щели. Странно, не правда ли? То, что мы делаем в начале XXI в., может изменить то, что случилось тысячи лет назад, когда этот электрон начинал свое путешествие. Создается впечатление, что существует не только множественное будущее, но и множественное прошлое, и акт наблюдения, произведенный в настоящем, может определить, что произошло в прошлом. Квантовая физика не только ставит под вопрос возможность познания будущего, но и заставляет усомниться в возможности действительного знания прошлого. Прошлое также представляется в виде суперпозиции возможностей, которые кристаллизуются только в случае наблюдения.
Расщепление личности
С моей точки зрения, интересная – и часто упускаемая из виду – особенность квантовой физики заключается в том, что вплоть до момента наблюдения она полностью детерминистична. Природа волнового уравнения, которое описывает электрон, пролетающий через щель, не вызывает никаких вопросов. Когда в 1926 г. Шредингер предложил свою теорию, он сформулировал дифференциальное уравнение, дающее полностью детерминистическое предсказание развития волновой функции. Волновое уравнение Шредингера в некотором смысле не менее детерминистично, чем уравнения движения Ньютона.
Вероятностные свойства и неопределенность возникают при попытке наблюдения частицы и извлечения классической информации. В высшей степени неклассическое и странное новое свойство заключается в этом разрывном переходе, по-видимому происходящем при «наблюдении» волны. Детерминизм внезапно исчезает, оставляя нам электрон, случайным образом расположенный в какой-то точке пространства. На большом масштабе такая случайность описывается информацией, содержащейся в волновой функции, но ученые пока не обнаружили механизма, который позволил бы определить в каждом индивидуальном случае будущее расположение электрона в конкретном эксперименте. Так ли это на самом деле? Действительно ли мы никогда не сможем определить положение электрона до наблюдения?
Когда мы производим наблюдение или измерение, происходит странный скачок, который привязывает частицу к одному определенному набору координат. Но немедленно после наблюдения эволюцию частицы начинает описывать другая волновая функция – и это положение сохраняется до следующего наблюдения и следующего скачка. Шредингеру чрезвычайно не нравились эти прерывистые изменения поведения: «Если нельзя избавиться от этих проклятых квантовых скачков, то я жалею, что вообще связался с квантовой теорией».
Тут важно не переборщить с оценкой роли человека. Можно предположить, что червяки тоже могут вызывать редукцию волновой функции. И измерения могут производить не только живые существа. На другом конце потенциально безжизненной Вселенной существуют частицы, взаимодействующие с неодушевленными объектами, и в результате такого взаимодействия волновая функция редуцируется для принятия решения о свойствах частицы. Такое взаимодействие является измерением ничуть не меньше, чем наши экспериментальные исследования в лаборатории. Вселенная заполнена излучением, которое освещает все, что оно встречает на своем пути. Может быть, именно поэтому Вселенная в целом кажется классической, а не пребывающей в постоянном состоянии неопределенности? Это предположение связано с концепцией, которую физики называют декогеренцией.
Мне очень трудно уместить в голове идею о том, что наблюдение становится точкой раздела между детерминистическим электроном, описываемым волновой функцией, и электроном, внезапно получающим точное, но абсолютно случайно определенное местоположение. Вся эта история кажется совершенно безумной. Тем не менее нельзя не признать, что она успешно работает в качестве инструмента для вычислений. Рассказывают, что физик Дэвид Мермин говорил тем, кого, как и меня, беспокоила такая неизвестность, «заткнитесь и считайте». По тому же принципу теория вероятностей применяется к броску игральной кости. Хотя движением кости управляют уравнения Ньютона, лучшим средством для вычисления ее возможного поведения остается теория вероятностей.
Но даже и заткнувшись я не могу избавиться от ощущения резонности таких возражений. Приборы, которые я использую для измерений, представляют собой физическую систему, состоящую из частиц, которые точно так же подчиняются законам квантовой физики, как и электрон, который я пытаюсь наблюдать. И сам я тоже! Я – всего лишь скопление частиц, подчиняющихся квантовым законам. Ведь любой наблюдатель, будь то фотопластинка или человек, является частью мира квантовой физики и тоже описывается волновой функцией. Взаимодействие между волновой функцией электрона и наблюдателем тоже должно описываться волной. В конце концов, в чем состоит «наблюдение» или «измерение»?
А если и наблюдатель, и частицы, пролетающие через щели, описываются волновыми функциями, то не может ли все быть детерминированным? Случайность внезапно исчезает. Почему же физики довольствуются заявлением о том, что акт наблюдения редуцирует волновую функцию, если на самом деле тут действует сверхфункция, описывающая всех участников процесса – и электрон, и приборы, и исследователя? Где проходит граница между квантовым миром вероятности и классическим миром определенности? Такое двойственное видение микроскопического квантового мира и макроскопического мира выглядит несколько подозрительно. Наверняка же можно описать все вместе неким волновым уравнением. Все это в высшей степени неудовлетворительно, но, по правде говоря, большинство физиков следуют совету Мермина и смиряются с таким положением вещей. Мой коллега Филип Канделас рассказывает, как один многообещающий студент, на которого все возлагали большие надежды, однажды вдруг пропал из виду. Когда Канделас поинтересовался, что с ним случилось, он узнал причину его исчезновения. Семейные обстоятельства? Болезнь? Долги? Ни то, ни другое, ни третье. «Он пытался понять квантовую механику».
Я, наверное, пренебрег советом, который Фейнман давал тем, кто подобно мне пытается добиться посвящения в квантовые тайны: «Если сможете, не мучайте себя вопросом “Но как же так может быть?”, ибо в противном случае вы зайдете в тупик, из которого еще никто не выбирался. Никто не знает, как же так может быть».
Тем не менее такую, по-видимому, встроенную в систему неопределенность пытались преодолеть несколькими разными способами. Один из них сводится к гипотезе, согласно которой в точке наблюдения реальность разделяется на суперпозицию разных реальностей. В каждой из них фотон или электрон имеет разные положения, так что волна в некотором смысле не редуцируется, но сохраняется и описывает развитие событий во всех этих разных реальностях. Однако, когда в игру вступает сознание, мы оказываемся заперты в одной из таких реальностей и не имеем доступа ко всем остальным, в которых фотон или электрон обнаруживаются в какой-либо другой точке фотопластинки.
Эта увлекательная попытка разобраться в сущности физики, известная под названием «многомировой интерпретации», была предложена в 1957 г. американским физиком Хью Эвереттом. Мне лично особенно интересно, можем ли мы вообще узнать, что такие многочисленные миры существуют одновременно с нашим. До сих пор никто не придумал способа проверить или исследовать такие миры – если они вообще есть. Теория утверждает, что существует всего одна волновая функция, описывающая развитие Вселенной совершенно детерминистическим образом. Следовательно, мы возвращаемся к воззрениям Ньютона и Лапласа – но с новым уравнением.
Наша проблема состоит в том, что мы – часть этой волновой функции и другие ее части для нас недоступны. Мы заключены в ней, заточены в одной из ветвей реальности, и то, что мы никогда не сможем познать другие миры, может быть неотъемлемой чертой нашего сознательного опыта. Но нельзя ли проанализировать, что происходит в других ветвях, при помощи математики? Я наблюдаю электрон в данной точке пластины детектора, но знаю при этом, что волновая функция описывает, что с ним происходит во всех других ветвях реальности. Разумеется, в этих многочисленных мирах существует не только электрон, но и «Я» – в других ветвях имеются копии меня, наблюдающие попадание электрона в другие участки пластины.
Эта модель реальности чрезвычайно интересна и, как кажется, непосредственно влияет на то, что мы называем сознанием. Мы еще вернемся к вопросу сознания на шестом «рубеже», но и эта глава ставит непростой вопрос: может ли сознание быть связано с поведением такой волновой функции? Почему мне известен лишь один результат попадания электрона в пластину? Является ли мое осознание того, что происходит вокруг меня, некоей разновидностью попадания электрона в детектор? Отсутствует ли у оборудования, установленного в моей голове, способность работать с множественными мирами? Когда я выглядываю в окно, фотоны, прилетающие от дома напротив, попадают в мой глаз и регистрируются сетчаткой. Почему, выглянув однажды в окно, я не могу увидеть, что дома номер 14 и 16 поменялись местами?
Пытаясь таким образом придать происходящему некоторую упорядоченность, мы подразумеваем, что скачок, порождаемый актом наблюдения, – не реальное событие, а нечто, происходящее в нашем уме. Наше восприятие говорит нам, что происходит скачок, но это не соответствует действительности. Однако такое объяснение вынуждает спросить: а что мы, собственно, делаем, когда даем миру научное объяснение?
Что такое наука? Как мы пытаемся исследовать свое взаимодействие со Вселенной? Если мы что-нибудь и узнаем, то только путем измерения и наблюдения. Математические уравнения могут сказать нам, чего ожидать, но без измерений такие предсказания остаются голой теорией. Поэтому довольно странно, что, для того чтобы «узнать» что-то о Вселенной, мы можем только наблюдать, тем самым заставляя частицы и свет решать, где они находятся и что они делают. Разве до этого не существовало ничего, кроме чистой фантазии? Мы не можем измерить всю волновую функцию, мы можем только познать ее математическими методами. Является ли квантовая волновая функция частью Вселенной, которую мы никогда не сможем познать – потому что, с нашей точки зрения, истинное познание невозможно без измерений? А измерение вызывает ее коллапс. Вероятно, вера в возможность знания, превышающего возможности измерения, – это проявление обычной жадности. Такое мнение выражал, например, Стивен Хокинг:
Я не требую, чтобы теория соответствовала реальности, потому что я не знаю, что такое реальность. Реальность – не такое качество, которое можно проверить лакмусовой бумажкой. Меня интересует только, чтобы теория правильно предсказывала результаты измерений.
Один вход, много выходов
С чем я действительно не могу примириться в основной современной интерпретации квантовой физики, так это с тем, что, поставив опыт с двойной щелью дважды с точным соблюдением одинаковых условий, можно получить разные результаты. Это противоречит всему тому, во что я верю. Именно поэтому меня привлекла математика: определенность доказательства существования бесконечного количества простых чисел означает, что в следующий раз, когда я проверю его, я не рискую внезапно обнаружить, что количество этих чисел стало конечным. Я считал, что естественные науки в конечном счете состоят из таких же определенностей, даже если человек не всегда может до них добраться. Когда я бросаю игральную кость, я соглашаюсь с математикой теории хаоса, утверждающей, что я, возможно, никогда не смогу рассчитать исход такого броска. Но эта математика, по крайней мере, говорит, что в случае точно такого же броска кость упадет той же стороной. Однако физика, созданная на этом «рубеже», ставит такой вывод под вопрос.
Вероятностный характер поведения игральной кости выражает недостаток информации. В квантовой физике речь не идет о незнании физиком полной картины. Даже полное знание всего не устраняет участия вероятности и случая. Согласно современной интерпретации квантовой физики, одна и та же начальная точка, одни и те же входящие данные могут породить разные исходы броска кости.
Кое-кто может усомниться в том, что говорить о точном повторении начальных условий опыта и процедуры его проведения вообще имеет смысл, – строго говоря, такое повторение невозможно. Точное воспроизведение локальных условий возможно, но эксперимент происходит во Вселенной, а Вселенная изменяется. Волновую функцию Вселенной невозможно перемотать назад и запустить заново. Вселенная – это одноразовый эксперимент, одной из частей волновой функции которого являемся мы. Каждое наблюдение изменяет волновую функцию Вселенной, и отменить такое изменение нельзя.
Но что, если реальность случайна и не так детерминистична, как мне того хотелось бы? Фейнман говорит в своих «Лекциях по физике»: «В настоящее время приходится ограничиваться расчетом вероятностей. Мы говорим “в настоящее время”, но мы очень серьезно подозреваем, что все это – уже навсегда и разгрызть этот орешек человеку не по зубам, ибо такова природа вещей».
Судя по всему, истинная случайность воплощена на моем столе не в игральной кости, привезенной из Лас-Вегаса, а в баночке урана, купленной в интернете.
Назад: Рубеж третий: Банка урана
Дальше: 6

