Квадратичные вычеты могут показаться типичным примером мудреных умствований, которые так любят математики-теоретики: интеллектуальной игрой, не имеющей никакого практического применения. Но было бы ошибкой думать, что математическая идея бесполезна, только потому, что она не проистекает очевидным образом из практических задач повседневной жизни. Ошибка также считать, что повседневная жизнь настолько прямолинейна, как кажется на поверхностный взгляд. Для изготовления даже такой простой вещи, как банка джема из супермаркета, нужно сварить стекло, вырастить сахарный тростник или сахарную свеклу, очистить сахар… и очень скоро вы обнаружите, что с головой погрузились в статистический анализ испытаний сортов растений на сопротивляемость болезням и в конструирование судов, используемых для перевозки различных компонентов готового продукта по всему земному шару. В мире, где живет 7 млрд человек, массовое производство продуктов питания не сводится к тому, чтобы просто собрать ягоды и сварить их.

Действительно, математики, которые первыми выдвинули эти идеи, не думали ни о каких конкретных практических приложениях для них; просто квадратичные вычеты показались им интересными. Но они также были убеждены, что их понимание станет новым мощным дополнением к математическому инструментарию. Практики не в состоянии пользоваться инструментом, пока его не существует. И хотя на первый взгляд может показаться, что разумнее подождать появления конкретной задачи, прежде чем придумывать инструменты, подходящие для ее решения, при таком подходе мы до сих пор жили бы в пещерах. «Зачем ты теряешь время, стуча камнем по камню, а, Уг? Тебе следовало бы стучать палкой по голове мамонта, как делают остальные мальчики».

У квадратичных вычетов множество самых разных применений. Один из моих любимых примеров – проектирование концертных залов. Музыка, отражаясь от плоского потолка, дает явственное эхо, которое искажает звук и вообще мешает слушать. С другой стороны, звукопоглощающий потолок делает звучание мертвым и смазанным. Для хорошей акустики звук должен отражаться, но в виде рассеянного отзвука, а не резкого эха. Поэтому архитекторы встраивают в потолок специальные рассеиватели. Вопрос в том, какой они должны быть формы.

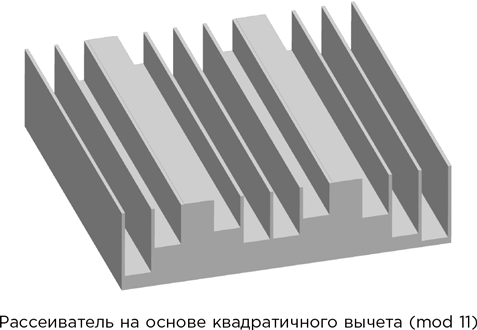
В 1975 г. Манфред Шрёдер изобрел рассеиватель, состоящий из серии параллельных борозд, глубина которых выводится из последовательности квадратичных вычетов для некоего простого модуля. Возьмем, к примеру, простое число 11. Мы только что видели, что квадраты чисел от 0 до 10 по модулю 11 равны:

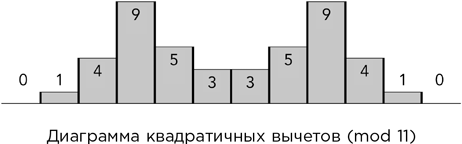
0 1 4 9 5 3 3 5 9 4 1,

и далее, для более крупных чисел, эта последовательность повторяется периодически. Она симметрична относительно середины, промежутка между двумя тройками, потому что x² = (–x)² по любому простому модулю. Сравним рисунок ниже – на нем эти числа показаны в виде прямоугольников – с формой рассеивателя на предыдущем рисунке. Обратите внимание: в данном случае глубина выемок получается путем вычитания вычетов из какой-то постоянной величины. Это не оказывает серьезного влияния на основной математический смысл.

Что такого особого в квадратичных вычетах? Одна из характеристик звуковой волны – ее частота: сколько волн приходит в ухо каждую секунду. Высокие частоты дают высокие звуки, низкие частоты – низкие звуки. Еще одна характеристика, связанная с частотой, – длина волны: расстояние между последовательными пиками. Высокочастотные волны короче, низкочастотные – длиннее. Колебания с заданной длиной волны резонируют с пустотами в поверхности, размеры которых близки к длине их волны. Так что волны разных частот по-разному реагируют на столкновение с поверхностью.

Рассеиватель на основе квадратичных вычетов обладает восхитительным математическим свойством: волны различных частот взаимодействуют с ним одинаково. Технически это означает, что преобразование Фурье постоянно на некотором диапазоне частот. Шрёдер указал на одно важное следствие: такая форма рассеивает звуковые волны многих разных частот одинаково. На практике ширина бороздок выбирается так, чтобы избежать диапазона волн, доступных для человеческого уха, а их длина кратна с определенным коэффициентом последовательности квадратичных вычетов, связанных с шириной.

Когда бороздки параллельны, как на рисунке, звук рассеивается в стороны, под прямым углом к бороздкам. Существует двумерный аналог этой системы – квадратное поле со стержнями, тоже рассчитанными на основе квадратичных вычетов, – который рассеивает звук равномерно во всех направлениях. Такие рассеиватели часто можно найти в звукозаписывающих студиях, где они помогают улучшить звуковой баланс и избавиться от лишних шумов.

Так что хотя Эйлер и Гаусс понятия не имели, для чего когда-нибудь будет использовано их изобретение и будет ли оно использовано хоть для чего-то, оно нередко играет принципиально важную роль (неявно, где-то за сценой), когда вы слушаете записанную музыку, будь то классика, джаз, кантри, рок, хип-хоп, кроссовер-трэш металлика – все что угодно.