В настоящее время нам известно десятичное значение π с точностью до 12 100 000 000 050 знаков; соответствующий расчет провел в 2013 г. Сигеру Кондо, и потребовалось ему на это 94 дня. На самом деле никому нет дела до того, какой получен ответ, но известно, что замечательные рекордные усилия такого рода нередко приводят к новым озарениям, а также являются хорошим способом проверки новых суперкомпьютеров. Одно из самых забавных открытий состоит в том, что можно вычислять отдельные цифры десятичной записи π без нахождения всех предыдущих цифр. Однако в настоящее время мы можем это делать только в шестнадцатеричной нотации, то есть в системе счисления с основанием 16, из которой можно без труда получить цифры в системах счисления с основаниями 8, 4 и 2 (двоичной). Эта идея работает и для других констант, не только для π, а также для троичной системы счисления, но систематической теории на этот счет пока нет. Для десятичной нотации, то есть для системы счисления с основанием 10, ничего подобного не известно.

Первоначальное открытие, формула ББП (Бейли – Боруэйна – Плаффа), изложена ниже; вы найдете ее также в «Кабинете…» на с. 264. Это бесконечный ряд, при помощи которого можно вычислить конкретный шестнадцатеричный знак числа π, не вычисляя при этом предыдущих его знаков. Так что мы можем быть уверены, что квадриллионный двоичный знак числа π – нуль, благодаря проекту PiHex; пройдя еще дальше, скажем, что двухквадриллионный двоичный знак π также равен 0, благодаря расчету, проведенному одним из сотрудников компании Yahoo! и занявшему 23 дня. Несмотря на все наши познания, для того чтобы найти предыдущий знак, потребовался бы еще один столь же длительный расчет.

В 2011 г. Дэвид Бейли, Джонатан Боруэйн, Эндрю Маттинли и Гленн Уайтвик составили обзорное исследование этого вопроса. Авторы описали способ нахождения знаков числа π² в системе счисления с основанием 64, знаков числа π² в системе счисления с основанием 729 и знаков числа, известного как постоянная Каталана, в системе счисления с основанием 4096, начиная с 10-триллионной позиции.

История начинается с последовательности, известной еще Эйлеру:

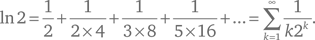
Благодаря степеням двойки, которые здесь фигурируют, этот ряд можно преобразовать в метод вычисления конкретных двоичных знаков ln 2. По мере роста номера знака вычисления остаются реализуемыми, хотя и занимают гораздо больше времени.

Формула ББП выглядит так:

и степени 16 делают возможным вычисление конкретных шестнадцатеричных знаков числа π. Поскольку 16 = 2⁴, ряд можно использовать также для вычисления двоичных знаков.

Ограничивается ли такой подход только этими двумя константами? С 1997 г. математики ведут непрекращающийся поиск аналогичных бесконечных рядов для других постоянных величин, и им уже удалось найти их немалое количество. В том числе для π², ln² 2, π ln 2, ζ (3), π³, ln³ 2, π²ln 2, π⁴, ζ (5),

где

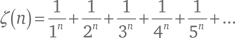
есть Риманова дзета-функция. Удалось сделать то же для постоянной Каталана

Некоторые из этих рядов дают знаки в троичной системе счисления или системе с основанием, равным какой-нибудь степени 3. К примеру, при помощи поразительной формулы Дэвида Броудхерста

можно вычислять знаки π² в системе счисления с основанием 729 = 3⁶.