Иногда математикам требуются более крупные числа, чем физикам. Не только, надо заметить, для развлечения: дело в том, что такие числа на самом деле иногда всплывают в разумных актуальных задачах. Число Грэма, названное в честь американца Рона Грэма, возникает в комбинаторике – математике подсчета различных способов перестановки объектов или выполнения каких-то условий.

В 1978 г. Грэм и Брюс Ротшильд работали над задачей о гиперкубах – многомерных аналогах куба. У квадрата 4 угла, у куба – 8, у четырехмерного гиперкуба – 16, а у n-мерного гиперкуба – 2ⁿ углов. Они соответствуют всем возможным последовательностям из n нулей и единиц в системе n координат.

Возьмем n-мерный гиперкуб и проведем линии, соединяющие все пары углов. Покрасим каждую линию либо в красный цвет, либо в синий. Для какого наименьшего n в любой схеме такой раскраски найдется по крайней мере один набор из четырех углов, лежащих на одной плоскости, таких, что все соединяющие их отрезки окрашены в один и тот же цвет?

Два упомянутых математика доказали, что такое число n существует, что далеко не очевидно. Ранее Грэм нашел более простое доказательство, но с использованием большего числа: в стрелочной нотации Кнута n, о котором идет речь, не превосходит

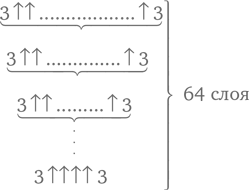
Здесь числа под горизонтальными фигурными скобками указывают, сколько стрелок стоит над соответствующей скобкой. Смотреть нужно снизу вверх, начиная с самой нижней строки: в предпоследнем (63-м) слое стоит 3↑↑↑↑3 стрелки. Далее, число с таким количеством стрелочек дает нам число стрелочек в следующем, 62-м слое. А число с таким количеством стрелочек – число стрелочек в 61-м слое!.. Извините, ни одно из этих чисел нельзя записать в стандартной десятичной нотации. В этом отношении они намного хуже гуголплекса. Но в этом и заключается их прелесть…

Это и есть число Грэма, и оно поистине громадно. Более чем. Величина, найденная Грэмом и Ротшильдом, меньше, но по-прежнему до безобразия велика, и объяснять ее сложнее, так что я не буду этим заниматься.

Как ни смешно, специалисты, работающие в этой области, считают, что это число можно сделать намного меньше. А именно, что годится даже n = 13. Но это пока не доказано. Грэм и Ротшильд доказали, что n не может быть меньше 6; Джефф Эксоо поднял эту величину до 11 в 2003 г.; наилучший результат на сегодняшний день гласит, что n не должно быть меньше 13, что доказал Джером Баркли в 2008 г.