Книга: Математические головоломки профессора Стюарта
Назад: Загадка песков
Дальше: Серьезный беспорядок
π для эскимосов
Почему π в Арктике равно всего лишь 3?
На холоде все съеживается.
Знак одного. Часть четвертая – завершение 
Из мемуаров доктора Ватсапа
– Да, это острая штучка, – пробормотал я.
– Корнишон, кажется, – заметил Сомс, выдергивая из банки маринованный огурчик и с наслаждением его пережевывая.
Я убрал острое лакомство обратно в буфет вместе с банкой.
– У нас и правда есть возможность, – заметил Сомс, – умножать числа на 3, 9 или 10 с использованием всего одной дополнительной единицы. Для этого достаточно разделить число на √(0,(1)), 0, (1) или 0,1.
– Тогда у меня есть вариант! – воскликнул я.
62 = 63 – 1 = 7 × 9–1 = 7/0,(1) – 1,
помня, что у нас уже есть выражение для 7 из двух единиц – и даже в двух различных вариантах.
– И у нас остается одна проблема – 138.
– Так, это 3 × 46, – размышлял я вслух. – Можем мы получить 46, используя всего три единицы? Тогда мы могли бы разделить его на√(0,(1)), как вы предлагали.
Систематическое исследование разных вариантов округления последовательных квадратных корней из факториалов привело нас к неожиданному открытию: 46 можно получить всего из двух единиц. Я покажу здесь только решение: на пути к нему нам пришлось обследовать множество тупиков и потерпеть немало неудач. Начать можно, к примеру, с представления 7 через две единицы:
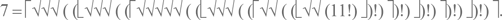
Затем заметим, что
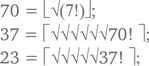
Двигаясь обратно и подставляя формулы для соответствующих чисел, получим выражение для 138 через три единицы.
– Записать все это явно, Сомс?
– Бога ради, не нужно! Всякий, кто захочет увидеть полную формулу, сможет сделать это самостоятельно.
Вдохновленный неожиданным успехом, я хотел продолжить наш список еще дальше, но Сомс только пожал плечами:
– Может, эта проблема заслуживает дальнейшего рассмотрения. А может, и нет.
Внезапно меня осенило:
– А не можем ли мы доказать, что любое число можно получить из четырех – или меньше – единиц путем подбора полов и потолков повторяющихся квадратных корней из факториалов?
– Вполне возможно, Ватсап, вполне возможно, но я, откровенно говоря, не вижу пути к такому доказательству, к тому же напряжение от такого количества ментальной арифметики начинается сказываться.
Прямо на глазах он вновь начал погружаться в депрессию. В отчаянии я предложил:
– Вы могли бы попробовать логарифмы, Сомс.
– Я думал о них в самом начале, Ватсап. Вы, вероятно, будете удивлены, но использование логарифмов экспоненциальной функции и функции потолка – ничего больше – позволяет выразить любое положительное целое число через одну-единственную единицу.
– Нет-нет, я говорил об использовании логарифмов для облегчения вычислений, а не в формулах… – но Сомс не обратил внимания на мои протесты.
– Вспомните, что представляет собой экспоненциальная функция:
exp (x) = ex, где e = 2,71828…
– Обратным по отношению к этой функции является натуральный логарифм
ln (x) = значение y, удовлетворяющее exp (y) = x.
– Не правда ли, Ватсап?
Я подтвердил, что, насколько мне известно, дело обстоит именно так.
– Тогда мы просто заметим, что
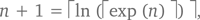
что несложно доказать.
Я посмотрел на него с открытым ртом, но сумел-таки выдавить из себя полузадушенное:
– Конечно, Сомс.
– В результате мы можем последовательно записать:
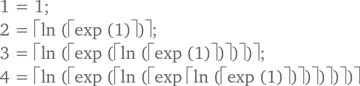
и…
Я поспешно схватил его за правую руку.
– Да, Сомс, я понимаю. Это слегка замаскированная версия метода Пеано, который мы ранее отвергли именно из-за его тривиальности.
– Так что, Ватсап, если разрешить экспоненциальные выражения и логарифмы, игра сразу же закончится.
Я согласился – не без грусти, поскольку он сразу же взял свой кларнет и вновь завел бесконечную пьесу какого-то малоизвестного восточноевропейского композитора, в которой не было ни ритма, ни мелодии. Звук походил на вопль кота, попавшего между валками для отжимания белья. Кота, которому медведь наступил на ухо. Притом охрипшего.
Черное настроение поглотило Сомса окончательно и бесповоротно.
На этом заканчивается «Знак одного».
Правда, я так и не рассказал вам, что такое субфакториал. Ну, ничего, в следующий раз.
Назад: Загадка песков
Дальше: Серьезный беспорядок

