Насколько эффективен алгоритм Евклида?

Отсекание по одному квадрату за раз проще для теоретических целей, но более компактная форма в терминах деления с остатком лучше подходит для практического использования. При этом вся работа с квадратами одного размера сокращается до одной операции.

Бóльшая часть вычислительных усилий при этом приходится на операцию деления, так что мы можем оценить эффективность алгоритма, подсчитав, сколько раз производится эта операция. Первым этот вопрос исследовал Антуан Рейно, в 1911 г. он доказал, что число операций деления в процедуре поиска НОД составляет максимум m, то есть не превышает меньшего из двух чисел. Это очень грубая оценка, и позже Рейно снизил ее до m/2 + 2, что ненамного лучше. В 1841 г. П. Финк снизил эту оценку до 2 log₂ m + 1, что пропорционально числу десятичных знаков в m. В 1844 г. Габриель Ламе доказал, что число операций деления не более чем в пять раз превосходит число десятичных знаков в m. Так что даже для двух чисел по 100 знаков каждое алгоритм позволяет получить ответ не более чем за 500 шагов. В целом можно сказать, что сделать это так же быстро с использованием простых множителей невозможно.

Что представляет собой наихудший сценарий? Ламе доказал, что алгоритм выполняется медленнее всего в том случае, когда m и n являются последовательными членами ряда Фибоначчи

1 1 2 3 5 8 13 21 34 55 89…,

в котором каждое следующее число представляет собой сумму двух предыдущих. Для этих чисел на каждом шаге от прямоугольника отсекается ровно один квадрат. К примеру, при m = 34, n = 55 получаем

деление 55 на 34 дает 1, остаток 21;

деление 34 на 21 дает 1, остаток 13;

деление 21 на 13 дает 1, остаток 8;

деление 13 на 8 дает 1, остаток 5;

деление 8 на 5 дает 1, остаток 3;

деление 5 на 3 дает 1, остаток 2;

деление 3 на 2 дает 1, остаток 1;

деление 2 на 1 дает 1 ровно.

Необычайно длинный расчет для таких небольших чисел.

Математики проанализировали также среднее число операций деления. При фиксированном n число таких операций, усредненное по всем меньшим m, составляет примерно

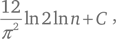
где C – так называемая постоянная Портера, равная

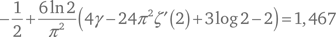
Здесь ζ'(2) – оценка производной от римановой дзета-функции в точке 2, а γ – постоянная Эйлера, равная 0,577. Было бы трудно найти разумную задачу, при решении которой в одной формуле собирается более представительная выборка математических констант. Отношение вычисленного по этой формуле значения к точному ответу стремится к 1 по мере возрастания n.