Это математическая загадка, которая была решена более двух тысяч лет назад и долгое время преподавалась в школах, но теперь уже не преподается – по разумным, вероятно, соображениям. Однако с ней стоит познакомиться, поскольку она намного эффективнее того метода, который используется вместо нее. Кроме того, она позволяет установить связь со многими важными математическими понятиями более высоких уровней.

Люди, как правило, любят выводить каракули. Нередко можно увидеть, как кто-то, разговаривая по телефону, бездумно заштриховывает шариковой ручкой, к примеру, все буквы «о» на газетной странице. Или выводит извилистые линии, которые длятся и длятся без конца, свиваясь в какие-то неправильные спирали. Слово doodle, обозначавшее первоначально глупца, впервые ввел, судя по всему, сценарист Роберт Рискин в комедии 1936 г. «Мистер Дидс переезжает в город»; в фильме мистер Дидс говорит о каракулях (doodle) как о средстве, помогающем человеку думать.

Если математик рисует каракули (а большинство из них грешат этим), он вполне может нарисовать, к примеру, прямоугольник. Что можно сделать с прямоугольником? Можно заштриховать его, можно закрутить вдоль сторон спиралеобразные линии… а можно отрезать от него кусок с одной стороны и получить прямоугольник поменьше. После этого естественно – и, кстати говоря, типично для ментальности рисовальщика каракулей – повторить проделанную процедуру.

Что при этом происходит? Может быть, вам, прежде чем читать дальше, захочется самому нарисовать пару прямоугольников.

Ну, хорошо, продолжаем. Я начал с длинного узкого прямоугольника, и вот что получилось.

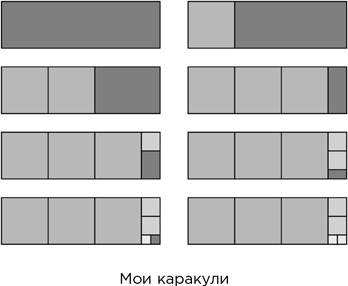
В конце концов я получил маленький квадратик, на котором мой прямоугольник закончился.

Всегда ли так получается? Всякий ли прямоугольник в конце концов заканчивается? Это хороший вопрос, способный дать математику пищу для размышлений.

Какого размера был мой прямоугольник? Ну, последний рисунок показывает, что:

• сумма сторон двух маленьких квадратиков равна стороне среднего квадрата;

• сумма сторон двух средних квадратов и одного маленького квадратика образует сторону большого квадрата и равна при этом одной из сторон прямоугольника;

• сумма сторон трех больших квадратов и одного среднего равна второй стороне прямоугольника.

Если сторона маленького квадратика равна единице, то сторона среднего квадрата равна 2, а сторона большого равна 2 × 2 + 1 = 5. Следовательно, короткая сторона прямоугольника равна 5, а длинная равна 3 × 5 + 2 = 17. Таким образом, я начал с прямоугольника размером 17 × 5.

Это интересно: глядя на то, как складываются квадраты, я могу определить размеры своего прямоугольника. Более тонкий момент: если процесс завершается, это означает, что обе стороны первоначального прямоугольника нацело делятся на одно и то же число – сторону последнего изъятого квадрата. Иными словами, отношение его сторон имеет форму p/q, где p и q – целые. Что делает его рациональным числом.

Это общая идея: если процесс деления на квадраты рано или поздно прекращается, значит, отношение сторон прямоугольника выражается рациональным числом. Более того, обратное тоже верно: если отношение сторон прямоугольника рационально, каракули рано или поздно закончатся. Так что «конечные» каракули в точности соответствуют «рациональным прямоугольникам».

Чтобы понять почему, взглянем на числа повнимательнее. По существу, рисунок сообщает нам следующее:

17 – 5 = 12;

12 – 5 = 7;

7 – 5 = 2.

После этого у нас остается прямоугольник 5 × 2 и пора переходить к среднему квадрату:

5 – 2 = 3;

3 – 2 = 1.

Остался прямоугольник 2 × 1, пора переходить к маленькому квадратику:

2 – 1 = 1;

1 – 1 = 0.

Стоп! И дело рано или поздно должно дойти до остановки, потому что все задействованные целые числа положительны и с каждым шагом они делаются все меньше и меньше. Так и должно быть, ведь мы каждый раз либо вычитаем из них что-то, либо оставляем, как есть. А последовательность положительных целых чисел не может уменьшаться до бесконечности. Если вы, к примеру, начнете с миллиона и будете все время уменьшать, то вам придется остановиться не более чем через миллион шагов.

Короче говоря, каракули сообщают нам вот что:

при делении 17 на 5 получается 3 с остатком 2;

при делении 5 на 2 получается 2 с остатком 1;

2 делится на 1 нацело с нулевым остатком,

а процесс останавливается, как только остаток становится равным нулю.

Евклид использовал подобные каракули для решения одной арифметической задачи: поиска наибольшего общего делителя для двух заданных целых чисел. Наибольший общий делитель – это наибольшее целое число, на которое оба заданных числа делятся нацело; его часто обозначают аббревиатурой НОД. К примеру, для чисел 4500 и 840 НОД равен 120.

Меня в школе учили искать НОД таким способом: разложить заданные числа на простые множители и посмотреть, какие множители у них окажутся общими. К примеру, пусть нам надо найти НОД чисел 68 и 20.

Раскладываем то и другое на простые множители:

68 = 2²× 17; 20 = 2²× 5.

НОД равен 2² = 4.

Применимость этого метода ограничена тем, что числа должны быть достаточно небольшими, чтобы их можно было быстро разложить на простые множители. Для более крупных чисел он совершенно неэффективен. Древние греки знали более эффективный способ – процедуру, которой они дали забавное название антифарезис. В данном случае ее применение выглядит так:

68 делим на 20, получаем 3 с остатком 8;

20 делим на 8, получаем 2 с остатком 4;

8 делим на 4, получаем 2 ровно.

Стоп!

Это тот же расчет, что мы проделали для 17 и 5, но теперь все числа вчетверо больше (но делятся они друг на друга столько же раз). Если вы расчертите прямоугольник 68 × 20 каракулями, то картинка получится та же, что и в прошлый раз, только последний маленький квадратик будет иметь размер 4 × 4, а не 1 × 1.

Техническое название этого метода – алгоритм Евклида. Вообще, алгоритм – это рецепт для расчета. Евклид поместил такой рецепт в свои «Начала» и использовал его в качестве основы для теории простых чисел. В символьном виде алгоритм каракулей выглядит так. Возьмем два положительных целых числа m£n. Начнем с пары (m, n) и заменим ее парой (m, n – m) в порядке величин, начиная с меньшего: то есть преобразуем

(m, n) → (min (m, n – m), max (m, n – m)),

где min и max обозначают, соответственно, минимум и максимум. Повторим процедуру. На каждом шаге большее число пары уменьшается, так что в конечном итоге процесс завершается, к примеру, парой (0, h). Тогда h и есть искомое НОД. Доказательство несложно: любой делитель m и n является также делителем (n – m) и наоборот. Поэтому на каждом шаге НОД обоих чисел пары не меняется.

Этот метод по-настоящему эффективен: с его помощью можно вычислять НОД вручную для действительно больших чисел. Чтобы доказать это, вот вам задание. Найдите НОД чисел 44 758 272 401 и 13 164 197 765.