Джон Мейсон и Теодорус Деккер нашли более простые методы доказательства невозможности, чем те, которыми пользовался Сверчковский. При склеивании двух одинаковых тетраэдров гранями каждый из них становится как бы отражением другого в их общей грани.

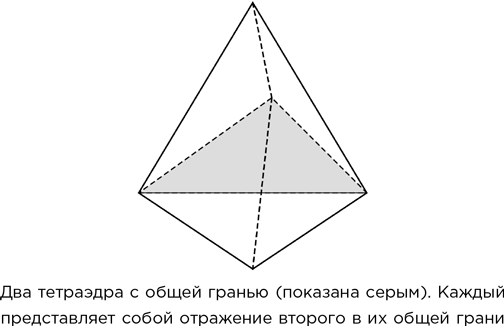
Начнем с одного тетраэдра. У него четыре грани и, соответственно, четыре таких отражения; назовем их r₁, r₂, r₃ и r₄. Каждое отражение ставит все на прежнее место, если проделать операцию дважды, так что r₁r₁ = e, где e – это нулевая трансформация («ничего не делать»). То же можно сказать и об остальных отражениях. Таким образом, все комбинации нескольких отражений представляют собой произведения вроде такого:

r₁r₄r₃r₄r₂r₁r₃r₁,

где последовательность индексов 14342131 может быть любой последовательностью чисел 1, 2, 3, 4, где ни одно число не встречается два раза подряд. К примеру, последовательности 14332131 быть не может. Причина в том, что здесь r₃r₃ – это одно и то же отражение, проделанное дважды, то есть e, которое не производит никакого действия и потому может быть исключено.

Если такая цепочка замыкается, то очередное отражение, примененное к крайнему тетраэдру в цепочке, дает тетраэдр, который совпадает с первоначальным. Таким образом, мы получаем уравнение вида

r₁r₄r₃r₄r₂r₁r₃r₁ = e

(только более длинное и сложное), где e означает «ничего не делать». Записав формулы для четырех отражений и воспользовавшись подходящими алгебраическими методами, можно доказать, что такое уравнение не выполняется никогда. Подробности см.:

T. J. Dekker, On reflections in Euclidean spaces generating free products, Nieuw Archief voor Wiskunde 7 (1959) 57–60.

M. Elgersma and S. Wagon, Closing a Platonic gap, Mathematical Intelligencer in the press.

J. H. Mason, Can regular tetrahedrons be glued together face to face to form a ring? Mathematical Gazette 56 (1972) 194–197.

H. Steinhaus, Problem 175, Colloquium Mathematicum 4 (1957) 243.

S. Swierczkowski, On a free group of rotations of the Euclidean space, Indagationes Mathematicae 20 (1958) 376–378.

S. Swierczkowski, On chains of regular tetrahedra, Colloquium Mathematicum 7 (1959) 9–10.