Книга: Математические головоломки профессора Стюарта
Назад: Непериодическая мостовая
Дальше: Теорема о четырех красках в пространстве
Теорема о двух красках 
Я ломал голову три часа кряду, но в конце концов сдался и попросил Сомса раскрыть секрет.
– Но потом вы скажете мне, как все абсурдно просто.
– Нет! Никогда!
– Позволю себе не согласиться, Ватсап. Потому что на этот раз все действительно просто до абсурдности, – молчание тянулось и тянулось, и он смилостивился: – Очень хорошо. Будем считать, что в нашем распоряжении имеется только черная и серая краска, а белым цветом отмечены еще не рассмотренные области. Начнем с того, что покрасим одну из областей в черный цвет (см. верхнюю левую фигуру на рисунке). После этого я выбираю одну из примыкающих областей и окрашиваю ее в серый цвет (верхняя средняя фигура). Затем окрашиваю примыкающую область черным, затем следующую – серым и т. д.
– Мне кажется, что после первого сделанного выбора во всех последующих случаях выбор делается вынужденно, – неуверенно сказал я.
– Да! Решение, если оно существует, должно быть единственным – с точностью до взаимной замены двух красок. И вы видите, что постепенно вся карта будет раскрашена с использованием только двух красок – черной и серой. Так что в данном случае, по крайней мере, решение существует.
– Согласен. Но я не до конца понимаю…
– Почему. Прекрасное замечание. На этот раз, мой дорогой Ватсап, вы попали в самую точку, а не по пальцу молотком. Проблема в том, чтобы доказать, что любая такая цепочка раскрашивания в черный и серый цвета приведет к одному и тому же результату, так? Потому что таким образом процесс не может привести к ситуации, для которой следующую оставшуюся область окрасить невозможно.
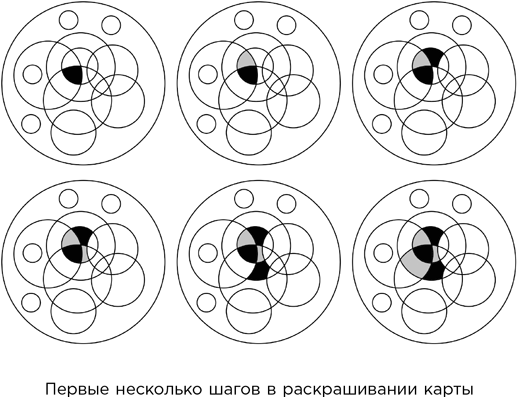
– Кажется, это я понимаю.
– Это можно сделать, – сказал Сомс. – Но есть более простой способ. Обратите внимание на то, что каждый раз, когда мы пресекаем общую границу, цвет меняется. Таким образом, если мы пересекаем нечетное число границ, то мы должны выбирать серый цвет, а если четное – то черный.
Я кивнул и тут же ляпнул:
– Но… как можем мы быть уверены, что не возникнет никаких противоречий?
Сомс блеснул улыбкой.
– Это потому, что мы можем, опираясь на только что мною сказанное, предписать каждой области вполне определенный цвет. Просто сосчитайте, в состав скольких кругов входит данная точка – конечно, точка не на окружности, потому что окружности мы не красим. Если это число четное, окрашиваем точку в черный цвет; если нечетное, окрашиваем в серый.
– Далее, пересечение любой границы либо добавляет к этому числу один дополнительный круг, либо вычитает из числа кругов единицу. В любом случае нечетное меняется на четное, а четное – на нечетное, так что цвет по разные стороны от этой границы должен быть разным.
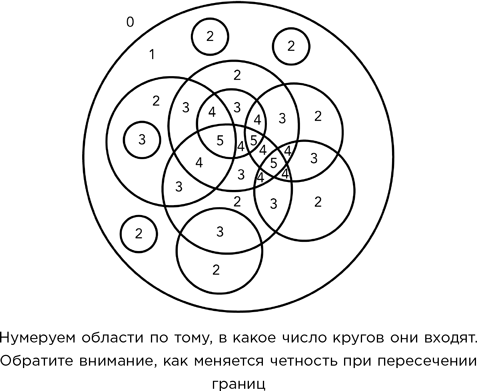
Доказательство оказалось ясным как божий день.
– Ну, Сомс…
– Конечно, – прервал он меня с легчайшим намеком на улыбку, – некоторые из окружностей могут касаться друг друга. Но и здесь действует тот же метод, нужно лишь правильно интерпретировать. Следует избегать пересечения границ в точке касания, и если немного подумать, то станет ясно, что это всегда можно сделать.
Ну, может, не совсем как божий день, но… да, я понял.
– Это… – начал я, но остановился, увидев выражение его лица, и закончил иначе:
– Очень умно.
Назад: Непериодическая мостовая
Дальше: Теорема о четырех красках в пространстве

