37
Формула Стирлинга утверждает, что n! приблизительно равно √(2πn)(n/e)n.
38
Леонардо нашел семейство решений
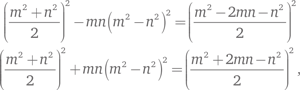
где m, n — нечетные числа. Роль d здесь выполняется числом mn (m² — n²2), а x равен m² + n²2/2. Выбор m = 5, n = 4 ведет к тому, что mn (m² — n²) = 720. Более того, 720 = 5 × 12². Разделив x на 12, получим ответ.

