25
Один корень p-й степени из единицы равен комплексному числу
ζ = cos2π/p + i sin2π/p,
а остальные представляют собой его степени ζ2, ζ3, … ζp−1. Чтобы понять почему, вспомните, что тригонометрические функции синус и косинус определяются через прямоугольный треугольник (см. рис. 56 слева). Обозначив стороны треугольника традиционными a, b, c, мы определяем синус и косинус угла A как sin A = a/c, cos A = b/c.
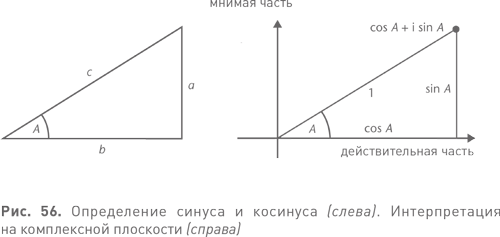
Если мы возьмем c = 1 и поместим этот треугольник на комплексную плоскость, как на рис. 56 справа, то вершина, в которой встречаются c и a, представляет собой точку
cos A + i sin A.
Несложно доказать, что для любых углов A и B
(cos A + i sin A) (cos B + i sin B) = cos (A + B) + i sin (A + B),
а это ведет непосредственно к формуле Муавра
(cos A + i sin A)n = (cos nA + i sin nA)
для любого натурального n. Поэтому
ζp = (cos 2π/p + i sin 2π/p)p = cos 2π + i sin 2π = 1
для любой степени 1, где ζ, ζ2, ζ3, …, ζp−1 есть корень p-й степени из единицы. На этом мы остановимся, поскольку ζp = 1 и, соответственно, для более высоких степеней новых чисел не появится.

