8
Вот красноречивый пример. Геометрически если прямая пересекается с окружностью и не является касательной, то она имеет с окружностью ровно две общие точки. Возьмем прямую, параллельную горизонтальной оси, на расстоянии 1/2 над ней (см. рис. 53). Эта прямая описывается очень простым уравнением: y = 1/2. (При любом x мы имеем одно и то же значение y.) Если y = 1/2, то уравнение x² + y² = 1 превращается в x² + 1/4 = 1. Отсюда x² = 3/4, а 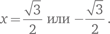 Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках
Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках 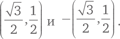 Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.
Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.
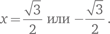 Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках
Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках 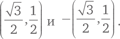 Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.
Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.


