14. Диофантовы мечты. Гипотеза Берча — Свиннертон-Дайера

В главе 7 мы уже встречались с «Арифметикой» Диофанта, и я упоминал о том, что 6 из 13 ее книг дошли до нас в греческих копиях. Примерно в 400 г. н. э., когда древнегреческая цивилизация уже давно находилась в упадке, лидерство в математической науке захватили Аравия, Китай и Индия. Арабские ученые перевели классические греческие работы, и сегодня мы знаем многие из них лишь по этим переводам. Именно в арабском мире развивались идеи Диофанта. Четыре арабские рукописи, найденные в 1968 г., могут быть переводами неизвестных до сих пор книг «Арифметики».

В какой-то момент в конце X в. персидский математик аль-Караджи задал вопрос, который, вполне возможно, приходил в голову и самому Диофанту: какие целые числа могут возникать в качестве одинаковой разности между тремя рациональными квадратами, образующими арифметическую последовательность? К примеру, целые квадраты 1,25 и 49 имеют общую разность 24. Иными словами, 1 + 24 = 25 и 25 + 24 = 49. Аль-Караджи жил примерно между 953 и 1029 гг., и он, в принципе, мог иметь доступ к списку «Арифметики», однако первый известный перевод сделал Абу-л-Вафа в 998 г. Леонард Диксон, автор краткой истории теории чисел в трех томах, предположил, что эта задача могла возникнуть незадолго до 972 г. в арабской рукописи неизвестного автора.

На алгебраическом языке задача звучит так: для каких целых d существует рациональное число x такое, что x — d, x и x + d являются полными квадратами? Ее можно сформулировать и иначе, хотя эквивалентность формулировок неочевидна: какие целые числа могут представлять собой площадь прямоугольного треугольника с рациональными сторонами? Иными словами, если a, b и c рациональны и a² + b² = c², то какие целые значения возможны для величины ab/2? Целые числа, удовлетворяющие этим эквивалентным условиям, называют конгруэнтными. Термин не имеет отношения к остальным случаям использования слова «конгруэнтный» в математике, и современного читателя это может несколько сбивать с толку. Его происхождение объясняется ниже.

Некоторые числа не являются конгруэнтными: к примеру, можно доказать, что 1, 2, 3 и 4 неконгруэнтны. С другой стороны, 5, 6 и 7, напротив, конгруэнтны. В самом деле, площадь треугольника со сторонами 3, 4, 5 равна 3 × 4/2 = 6, что доказывает конгруэнтность числа 6. Чтобы доказать конгруэнтность числа 7, заметим, что треугольник со сторонами (24/5)², (35/12)² и (337/60)² также прямоугольный и его площадь равна 7. К числу 5 я вернусь чуть позже. Рассматривая числа поочередно, одно за другим, мы получим длинный список конгруэнтных чисел, но вряд ли прольем много света на их природу. Никакое количество конкретных примеров не докажет, что какое-то конкретное целое число не является конгруэнтным. Несколько сотен лет никто не мог сказать, конгруэнтно число 1 или нет.

Сегодня мы знаем, что эта задача далеко выходит за рамки всего, что Диофант хотя бы в принципе мог решить. Более того, этот обманчиво простой вопрос полностью не разрешен до сих пор. Максимум, что нам удалось получить, — характеризация конгруэнтных чисел, открытая Джеральдом Таннеллом в 1983 г. Идея Таннелла позволяет получить алгоритм для определения, может ли данное целое число возникать в соответствующих ситуациях при помощи расчета его представлений в виде двух различных комбинаций квадратов. При небольшой изобретательности этот расчет годится для достаточно больших целых чисел. Эта характеризация имеет всего один серьезный недостаток: никто еще не доказал, что она верна. Ее адекватность зависит от решения одной из задач тысячелетия — гипотезы Берча — Свиннертон-Дайера. Эта гипотеза предлагает критерий, при котором эллиптическая кривая имеет конечное число рациональных точек. Мы уже встречали эти диофантовы уравнения в главе 6 (гипотеза Морделла) и главе 7 (Великая теорема Ферма). В этой главе мы еще раз увидим, какую выдающуюся роль они играют в теории чисел.

Самая ранняя из европейских работ, посвященных этим вопросам, принадлежит перу Леонардо Пизанского. Нам Леонардо по прозвищу Фибоначчи известен прежде всего благодаря последовательности странных чисел, которую он, судя по всему, изобрел. Числа эти возникали в ходе решения арифметической задачи о размножении каких-то невероятных кроликов. Вот числа Фибоначчи:

В этом ряду каждое число после двух первых представляет собой сумму двух предыдущих чисел. Отцом Леонардо был таможенный чиновник по имени Боначчо, и знаменитое прозвище означает «сын Боначчо». У нас нет никаких данных о том, что это прозвище использовалось при жизни Леонардо. Считается, что его придумал французский математик Гийом Либри в XIX в. Как бы то ни было, числа Фибоначчи широко известны и обладают множеством поразительных свойств. Они даже фигурируют в крипто-конспирологическом триллере Дэна Брауна «Код да Винчи».

Леонардо представил свои числа Фибоначчи в учебнике по арифметике «Книга счета» (Liber Abbaci), написанном в 1202 г. Основной целью учебника было привлечь внимание европейцев к придуманной арабами новой форме записи чисел, в основе которой лежали десять цифр от 0 до 9, и продемонстрировать ее универсальность. Сама идея десятичной записи уже достигла Европы через текст аль-Хорезми 825 г., названный в латинском переводе «Об индийском счете» (Algoritmi de Numero Indorum), но книга Леонардо стала первой из тех, что были написаны именно для того, чтобы способствовать внедрению десятичной системы в Европе. Значительная часть книги посвящена практической арифметике, в первую очередь операциям по обмену денег. Кроме этого, Леонардо написал еще одну книгу. Она не так известна, хотя во многих отношениях является непосредственным преемником диофантовой «Арифметики». Называется она «Книга квадратов» (Liber Quadratorum).

Подобно Диофанту, Леонардо представлял общие методики через конкретные примеры. Один из них основывался на вопросе аль-Караджи. В 1225 г. Пизу посетил император Фридрих II. Он был наслышан о Леонардо и его математических занятиях и, судя по всему, решил, что будет забавно объявить математический турнир и посмотреть на него в деле. В то время подобные публичные состязания были обычным делом. Участники задавали друг другу вопросы. В команду императора входили Джованни из Палермо и магистр Теодор. В команду Леонардо входил только сам Леонардо. Команда императора попросила Леонардо найти такой квадрат, который остался бы квадратом, если вычесть из него или прибавить к нему 5. Как обычно, все числа должны были быть рациональными. Иными словами, соперники хотели, чтобы Леонардо доказал, что 5 — число конгруэнтное, отыскав конкретное рациональное число x, для которого x − 5, x и x + 5 являются квадратами.

Эту задачу ни в коем случае нельзя назвать простой — самое краткое ее решение таково:

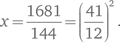
В этом случае

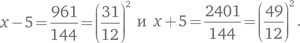
Леонардо нашел решение и включил его в «Книгу квадратов». Он получил ответ при помощи общей формулы, связанной с формулой Евклида/Диофанта для пифагоровых троек. Из нее Леонардо получил три целых квадрата с общей разностью 720, а именно: 31², 41² и 49². Затем он разделил их на 12² = 144, чтобы получить три квадрата с общей разностью 720/144, что равняется 5. В терминах пифагоровых троек можно взять треугольник со сторонами 9, 40 и 41 и площадью 180 и разделить на 36. Получим треугольник со сторонами 20/3, 3/2, 41/6. Площадь его равняется 5.

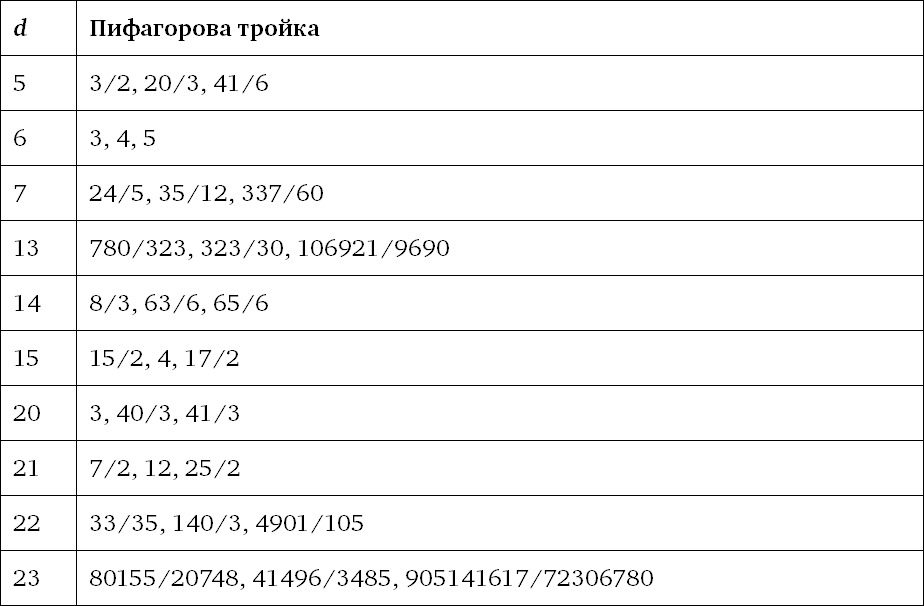
Именно у Леонардо мы находим латинское слово congruum для обозначения набора из трех квадратов в арифметической прогрессии. Позже Эйлер пользовался словом congruere, «сходятся». Первые десять конгруэнтных чисел и соответствующие простейшие пифагоровы тройки приведены в табл. 3. Никаких простых закономерностей здесь не видно.

Таблица 3. Первые десять конгруэнтных чисел и соответствующие им пифагоровы тройки

Первоначальным прогрессом в этом вопросе мы обязаны в первую очередь арабским математикам, показавшим, что числа 5, 6, 14, 15, 21, 30, 34, 65, 70, 110, 154 и 190, а также еще 18 больших чисел, являются конгруэнтными. Леонардо, Анджело Дженокки (1855) и Андре Жерарден (1915 г.) добавили к этим числам 7, 22, 41, 69, 77 и еще 43 числа, не превосходящих 1000. Леонардо в 1225 г. объявил, что число 1 не конгруэнтно, но не привел никаких доказательств. В 1569 г. Ферма доказал это. К 1915 г. все конгруэнтные числа меньше 100 были определены, но проблема плохо поддавалась решению, и еще в 1980 г. статус многих чисел меньше 1000 оставался неопределенным. О сложности проблемы можно судить по тому, как Л. Бастьен открыл конгруэнтность числа 101. Стороны соответствующего прямоугольного треугольника равны:

Он нашел эти числа в 1914 г. вручную. К 1986 г., когда считать благодаря компьютерам стало проще, Г. Крамарц нашел все конгруэнтные числа до 2000.

В какой-то момент было замечено, что другое, но связанное с этой задачей уравнение y² = x³ — d²x имеет решение x, y в целых числах тогда и только тогда, когда d конгруэнтно. В одном направлении это наблюдение очевидно: правая часть уравнения представляет собой произведение x, x — d и x + d, а если все сомножители являются квадратами, то квадратом является и произведение. Обратное утверждение получить также несложно. Такая формулировка задачи сразу переводит ее в богатые и процветающие владения теории чисел. Для любого заданного d это уравнение задает y², равный кубическому многочлену от x, и таким образом определяет эллиптическую кривую. Так что проблема конгруэнтных чисел — частный случай вопроса, ответить на который мечтают многие специалисты по теории чисел: при каких условиях эллиптическая кривая содержит хотя бы одну рациональную точку? Вопрос этот далеко не очевиден, даже для только что упомянутого частного случая эллиптической кривой. К примеру, 157 — число конгруэнтное, но гипотенуза простейшего прямоугольного треугольника с такой площадью равна

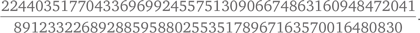
Прежде чем продолжить, мы позаимствуем у Леонардо его уловку — ту самую, что помогла перейти от 720 к 5, — и применим ее в самом общем виде. Умножив любое конгруэнтное число d на квадрат n² целого n, мы получим также конгруэнтное число. Чтобы убедиться в этом, достаточно взять любую рациональную пифагорову тройку, соответствующую треугольнику с площадью d, и умножить стороны на n. Площадь треугольника увеличится в n² раз. То же произойдет и при делении на n; площадь уменьшится в n² раз. Результат этого процесса будет целым только в том случае, если площадь делится нацело на квадрат целого числа (т. е. имеет квадратный делитель), так что при поиске конгруэнтных чисел достаточно работать только с числами, не имеющими такого делителя. Приведем первые несколько чисел, не имеющие квадратного делителя:

Теперь можно сформулировать критерий Таннелла. Нечетное число d, не имеющее квадратных делителей, конгруэнтно тогда и только тогда, когда число (положительных или отрицательных) целых решений x, y, z уравнения

точно вдвое превосходит число решений уравнения

Четное число d, не имеющее квадратных делителей, конгруэнтно тогда и только тогда, когда

точно вдвое превосходит число решений уравнения

Эти результаты куда полезнее, чем может показаться на первый взгляд. Поскольку все коэффициенты уравнения положительны, x, y и z по модулю не могут превосходить некие числа, кратные корню квадратному из d. Из этого следует, что число решений конечно и их можно найти систематическим поиском с применением некоторых полезных уловок. Приведем полный расчет нескольких примеров с небольшими d:

• Если d = 1, то единственными решениями первого уравнения являются x = 0, y = ±1, z = 0. То же относится и ко второму уравнению. Так что оба уравнения имеют по два решения, и, следовательно, критерий не выполняется.

• Если d = 2, то единственными решениями первого уравнения являются x = ±1, y = 0, z = 0. То же относится и ко второму уравнению. Так что оба уравнения имеют по два решения, и, следовательно, критерий не выполняется.

• Если d = 3, то единственными решениями первого уравнения являются x = ±1, y = ±1, z = 0. То же относится и ко второму уравнению. Так что оба уравнения имеют по четыре решения, и, следовательно, критерий не выполняется.

• Если d = 5 или 7, то первое уравнение не имеет решений. То же относится и ко второму уравнению. Поскольку дважды нуль равняется нулю, критерий выполняется.

• Если d = 6, то мы должны использовать критерий для четных чисел. Здесь опять же оба уравнения не имеют решений, и критерий выполняется.

Эти простые расчеты показывают, что 1, 2, 3, 4 (= 2² × 1) не являются конгруэнтными, а 5, 6 и 7 — являются. Анализ несложно продолжить, и в 2009 г. команда математиков применила тест Таннелла ко всем числам до триллиона, обнаружив при этом ровно 3 148 379 694 конгруэнтных числа. Исследователи проверили результат, повторив все расчеты дважды на разных компьютерах с использованием разных алгоритмов и программ, написанных двумя независимыми группами программистов. Билл Харт и Гонсало Торнариа пользовались компьютером Selmer в Уорикском университете. Марк Уоткинс, Дэвид Харви и Роберт Брэдшоу работали с компьютером Sage в Вашингтонском университете.

Однако во всех этих расчетах есть пробел. Таннелл доказал, что, если число d конгруэнтно, оно должно удовлетворять его критерию. Таким образом, если критерий не выполняется, число не конгруэнтно. Однако он не сумел доказать обратного: если число удовлетворяет его критерию, то оно обязательно конгруэнтно. Именно это необходимо нам, чтобы сделать вывод о конгруэнтности чисел 5, 6 и 7. В данных конкретных случаях мы можем найти подходящие пифагоровы тройки, но в общем случае это нам не поможет. Таннелл сумел показать, что обратное утверждение, о котором идет речь, непосредственно следует из гипотезы Берча — Свиннертон-Дайера, но она тоже пока не доказана.

Гипотезу Берча — Свиннертон-Дайера, как и несколько других задач тысячелетия, сложно даже сформулировать. (А вы думали, что можно получить миллион долларов, сделав что-нибудь простое?) Однако настойчивость всегда окупается, ведь в процессе работы мы осознаем глубину и оцениваем давние исторические традиции теории чисел. Если вы внимательно посмотрите на название гипотезы, то заметите, что одно тире в нем длиннее другого. Дело в том, что эту гипотезу выдвинули не математики Берч, Свиннертон и Дайер, а Брайан Берч и Питер Свиннертон-Дайер. Ее полная формально-математическая формулировка сложна для непосвященных, но речь в ней идет о фундаментальном вопросе диофантовых уравнений — алгебраических уравнений, решения которых ищутся в целых или рациональных числах. Вопрос этот предельно прост: при каких условиях эти уравнения имеют решения?

В главе 6, где речь шла о гипотезе Морделла, и в главе 7, посвященной Великой теореме Ферма, мы встретились с одним из чудеснейших инструментов математики — эллиптическими кривыми. Морделл в свое время высказал, как тогда казалось, случайную догадку, предположив, что число рациональных решений алгебраического уравнения с двумя переменными зависит от топологии соответствующей комплексной кривой. Если род равен 0 — кривая топологически представляет собой сферу, — решения задаются формулой. Если род равен 1 — кривая топологически представляет собой тор, т. е. является эллиптической кривой, — то все рациональные решения могут быть построены из подходящего конечного списка путем приложения структуры группы. Если род равен 2 или больше — кривая топологически представляет собой тор с g отверстиями, где g ≥ 2, — то число решений конечно. Как мы уже видели, Фальтингс доказал эту замечательную теорему в 1983 г.

Рациональные решения уравнений эллиптических кривых обладают одним поразительным свойством: благодаря геометрической конструкции, показанной на рис. 28 в главе 6, они образуют группу. Получившаяся структура называется группой Морделла — Вейля, и специалисты по теории чисел очень хотели бы иметь возможность вычислять ее. Для этого нужно найти систему генераторов: рациональных решений, из которых при помощи оператора группы могут быть получены все остальные. Если это не удается, то хотелось бы по меньшей мере определить основные характеристики группы, хотя бы ее величину. Здесь, однако, многое еще непонятно. Иногда группа бесконечна и порождает бесконечно много рациональных решений, иногда конечна, и тогда число рациональных решений тоже конечно. Было бы полезно иметь возможность определить, к какой категории относится конкретный случай. Но что нам по-настоящему хотелось бы знать, так это абстрактную структуру группы.

Доказательство Морделла, что конечный список генерирует все решения, говорит о том, что группа должна состоять из конечной группы и решетчатой группы. Решетчатая группа включает в себя все списки целых чисел конкретной конечной длины. Если длина чисел, к примеру, три, то группа состоит из всех списков (m₁, m₂, m₃) целых чисел, и эти списки складываются очевидным образом:

Длина списка называется рангом группы (и геометрически представляет собой размерность решетки). Если ранг группы 0, группа конечна. Если ранг не равен нулю, группа бесконечна. Поэтому, чтобы понять, сколько существует решений, нам необязательно знать полную структуру группы. Достаточно знать ее ранг. Именно об этом говорит гипотеза Берча — Свиннертон-Дайера.

В 1960-е гг., когда компьютеры только-только входили в нашу жизнь, одна из первых таких машин появилась в Кембриджском университете. Называлась она EDSAC, что означало «электронно-счетная машина с запоминающим устройством на линиях задержки». Название показывает, как гордились создатели этой машины устройством ее памяти, посылавшей звуковые волны по трубкам с ртутью и затем направлявшей их вновь к началу. Размером этот компьютер был с большой грузовик. Я хорошо помню, как в 1963 г. мне устроили экскурсию по нему. Цепи компьютера были сделаны на основе тысяч ключей — электронных ламп. Вдоль всех стен стояли широкие стеллажи с запасными лампами, которые то и дело надо было менять — так часто они сгорали.

Питера Свиннертон-Дайера эллиптические кривые интересовали с диофантовой стороны: в первую очередь ему хотелось понять, сколько существовало бы решений, если заменить кривую ее аналогом на конечном поле с простым числом p элементов. Иными словами, ему хотелось изучить применявшуюся Гауссом уловку с работой «по модулю p». При помощи компьютера он вычислял эти числа для большого числа простых и искал среди них интересные закономерности.

Постепенно у него появились определенные подозрения. Его научный консультант Джон Кассельс испытывал сильные сомнения, но по мере появления все новых и новых данных он тоже поверил, что в этой идее что-то есть. Компьютерные эксперименты, проведенные Свиннертон-Дайером, указывали вот на что. У специалистов по теории чисел есть стандартный метод записи любого уравнения в целых числах по определенному модулю — вспомните модулярную арифметику или «арифметику часов» по модулю 12 в главе 2. Поскольку все законы алгебры приложимы в этом варианте арифметики, любое решение первоначального уравнения становится и решением «урезанного» уравнения по этому модулю. Все задействованные числа образуют конечный список — к примеру, для арифметики часов в этом списке всего 12 чисел, — поэтому все решения можно найти методом проб и ошибок. В частности, для каждого заданного модуля можно подсчитать, сколько существует решений. Кроме того, решения по каждому модулю накладывают определенные ограничения на решения первоначального уравнения и иногда даже помогают доказать, что такие решения существуют. Поэтому у специалистов по теории чисел выработался рефлекс рассматривать варианты любого уравнения по разным модулям, и простые числа особенно полезны в качестве таковых.

Таким образом, чтобы выяснить что-нибудь полезное об эллиптической кривой, можно рассмотреть все простые числа до определенного предела. Для каждого простого числа можно определить, сколько точек лежит на кривой по модулю этого числа. Берч заметил, что компьютерные эксперименты Свиннертон-Дайера показывают интересную закономерность, если разделить число таких точек на простое число, по модулю которого все рассматривалось. Затем следует перемножить результаты такого деления для всех простых чисел до заданного предела включительно и отложить результаты для последовательных простых чисел на логарифмической бумаге. Интересно, что все данные ложатся недалеко от прямой линии, крутизна которой представляет собой ранг данной эллиптической кривой. Это позволяло предложить гипотетическую формулу для числа решений, связанных с любым простым модулем.

Источник этой формулы, однако, не теория чисел: в ней задействован комплексный анализ, очень любимый в XIX в. и, по счастливому стечению обстоятельств, гораздо более элегантный, чем старомодный действительный анализ. В главе 9, посвященной гипотезе Римана, мы видели, как анализ вытягивает свои щупальца во всех направлениях и проникает в близкие и не очень области математики. Особенно удивительные и мощные связи возникли у него с теорией чисел. Формула Свиннертон-Дайера позволила выдвинуть более подробную гипотезу о типе комплексной функции (я упоминал ее в главе 9), известной как L-функция Дирихле. Эта функция аналогична для эллиптических кривых известной дзета-функции Римана. Эти два математика, очевидно, пытались обогнать время — ведь тогда не было даже наверняка известно, что у каждой эллиптической кривой есть L-функция Дирихле. Это было достаточно произвольное предположение, в пользу которого почти не было данных, но чем дальше шло развитие, тем правдоподобнее казалось это предположение. Это был не прыжок в неведомое, а изумительно точное и дальновидное проявление утонченной математической интуиции. Вместо того чтобы подняться на плечах гигантов, как чаще всего бывает в науке, Берч и Свиннертон-Дайер поднялись на собственных плечах — они были способны самостоятельно держаться в воздухе.

Основной инструмент комплексного анализа — выражение функции в виде степенного ряда, похожего на многочлен, но содержащего бесконечно много слагаемых с все более и более высокими степенями переменной, которую в этой области традиционно обозначают s. Чтобы выяснить, что функция делает около какой-то конкретной точки, скажем, 1, следует использовать степени (s − 1). Гипотеза Берча — Свиннертон-Дайера утверждает, что если разложение L-функции Дирихле в степенной ряд возле 1 выглядит как

где c — ненулевая константа, то ранг кривой равен r, и наоборот. На языке комплексного анализа это утверждение принимает вид: L (C, s) имеет в точке s = 1 нуль r-го порядка.

Главное здесь — не точное выражение, о котором идет речь; главное — то, что для любой заданной эллиптической кривой существует аналитическая формула с использованием соответствующей комплексной функции, при помощи которой можно точно узнать, сколько независимых рациональных решений необходимо найти, чтобы определить их все.

Возможно, простейший способ продемонстрировать, что гипотеза Берча — Свиннертон-Дайера имеет смысл и значение, — это упомянуть о том, что максимальный известный ранг равен 28. Иными словами, существует эллиптическая кривая с набором из 29 рациональных решений, позволяющим получить все остальные рациональные решения. Более того, меньшего набора рациональных решений, который позволял бы это сделать, не существует. Хотя известно, что кривые такого ранга существуют, конкретных примеров до сих пор не найдено. Максимальный ранг, для которого имеется конкретный пример, равен 18. Соответствующую кривую нашел в 2006 г. Ноам Элкис, и выглядит она так:

Я привел нестандартный вид «y² = кубический многочлен от x», но данную запись можно привести к стандартному виду за счет дополнительного увеличения коэффициентов. Считается, что ранг может быть сколь угодно большим, но это до сих пор не доказано. Если судить по уже имеющимся данным, ранг не может быть больше некоего фиксированного числа.

Большая часть утверждений, которые мы можем доказать, относится к кривым рангов 0 и 1. Если ранг равен 0, то существует конечное число рациональных решений. Если ранг равен 1, то одно конкретное решение позволяет получить почти все остальные, за исключением, возможно, конечного числа решений. Эти два случая включают все эллиптические кривые вида y² = x³ + px, где p — простое число вида 8k + 5 (такое, как 13, 29, 37 и т. д.). Предполагается, что в этих случаях ранг всегда равен 1, что подразумевает существование бесконечного числа рациональных решений. Эндрю Бремнер и Кассельс доказали верность этого утверждения для всех простых чисел соответствующего вида до 1000. Оказалось, что, даже если ранг известен и мал, найти решения, позволяющие получить почти все остальные, может быть очень трудно. Они выяснили, что для p = 877 простейшим решением такого рода является рациональное число

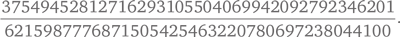
Доказано огромное число теорем, имеющих отношение к гипотезе Берча — Свиннертон-Дайера (обычно с очень серьезными формальными ограничениями), но это пока мало помогло в продвижении к полному решению этой задачи. В 1976 г. Коутс и Уайлс обнаружили первые указания на то, что эта гипотеза может быть верна. Они доказали, что один частный случай эллиптической кривой имеет ранг 0, если L-функция Дирихле не обращается в нуль в точке 1. Для такой эллиптической кривой число решений связанного с ней диофантова уравнения конечно, возможно, равно нулю, и определить это можно по соответствующей L-функции. После этого момента удалось сделать несколько технических шагов, по-прежнему ограниченных в основном рангами 0 и 1. В 1990 г. Виктор Колывагин доказал, что гипотеза Берча — Свиннертон-Дайера верна для рангов 0 и 1.

Более детальные гипотезы, требующие серьезной компьютерной поддержки, соотносят константу c в гипотезе Берча — Свиннертон-Дайера с различными концепциями теории чисел. Существуют аналогичные гипотезы — впрочем, столь же загадочные, — для алгебраических числовых полей. Известно также, что большинство (в точном смысле) эллиптических кривых имеет ранг 0 или 1. В 2010 г. Манджул Бхаргава и Арул Шанкар объявили, что им удалось доказать: средний ранг эллиптической кривой не превосходит 7/16. Если это доказательство и доказательство некоторых других недавно опубликованных теорем будут признаны математическим сообществом, то получится, что гипотеза Берча — Свиннертон-Дайера верна для ненулевой доли всех эллиптических кривых. Однако речь пока идет о простейших кривых, не представляющих, по существу, кривые более сложной структуры, ранга 2 и более. Они пока остаются для нас загадкой.